Semantic Security for Quantum Wiretap Channels
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Birth and Evolution of Korean Reality Show Formats
Georgia State University ScholarWorks @ Georgia State University Film, Media & Theatre Dissertations School of Film, Media & Theatre Spring 5-6-2019 Dynamics of a Periphery TV Industry: Birth and Evolution of Korean Reality Show Formats Soo keung Jung [email protected] Follow this and additional works at: https://scholarworks.gsu.edu/fmt_dissertations Recommended Citation Jung, Soo keung, "Dynamics of a Periphery TV Industry: Birth and Evolution of Korean Reality Show Formats." Dissertation, Georgia State University, 2019. https://scholarworks.gsu.edu/fmt_dissertations/7 This Dissertation is brought to you for free and open access by the School of Film, Media & Theatre at ScholarWorks @ Georgia State University. It has been accepted for inclusion in Film, Media & Theatre Dissertations by an authorized administrator of ScholarWorks @ Georgia State University. For more information, please contact [email protected]. DYNAMICS OF A PERIPHERY TV INDUSTRY: BIRTH AND EVOLUTION OF KOREAN REALITY SHOW FORMATS by SOOKEUNG JUNG Under the Direction of Ethan Tussey and Sharon Shahaf, PhD ABSTRACT Television format, a tradable program package, has allowed Korean television the new opportunity to be recognized globally. The booming transnational production of Korean reality formats have transformed the production culture, aesthetics and structure of the local television. This study, using a historical and practical approach to the evolution of the Korean reality formats, examines the dynamic relations between producer, industry and text in the -

Brushless Servo Motors Bsm132 Thrust Load Capacities
— Brushless Servo Motors Installation and Operating Manual July 2020 — MN1240_July 2020 Any trademarks used in this manual are the property of their respective owners. Note: Baldor Electric Company, became ABB Motors and Mechanical, Inc. on March 1, 2018. Nameplates, Declaration of Conformity and other collateral material may contain the company name of Baldor Electric Company and the brand names of Baldor-Dodge and Baldor-Reliance as well as the company name of ABB until such time as all materials have been updated to reflect our new corporate identity of ABB. Table of Contents Section 1 General Information . 1-1 Overview . 1-1 Safety Notice . 1-1 Section 2 Installation . 2-1 Overview . 2-1 Location . 2-1 Alignment . 2-1 Receiving . 2-2 Storage . 2-2 Unpacking . 2-2 Handling . 2-2 Repairs . .. 2-2 Prevent Electrical Noise . 2-2 Shaft Loads . 2-3 Life Determination . 2-5 Speed and Torque . .. 2-7 Holding Brake . 2-7 Electrical Connections . 2-8 Motor Lead Termination . 2-9 Strain Relief (Mounted at Terminal Box) . 2-9 Feedback Termination . 2-9 Feedback Devices . 2-13 Brushless Servo Motor Identification . 2-15 MN1240 i ii MN1240 Section 1 General Information Overview This manual contains general procedures that apply to ABB Motor products. Be sure to read and understand the Safety Notice statements in this manual. For your protection, do not install, operate or attempt to perform maintenance procedures until you understand the Warning and Caution statements. A Warning statement indicates a possible unsafe condition that can cause harm to personnel. A Caution statement indicates a condition that can cause damage to equipment. -

Download Rock Over the Edge: Transformations in Popular Music
Rock Over the Edge: Transformations in Popular Music Culture, Roger Beebe, Denise Fulbrook, Ben Saunders, Duke University Press, 2002, 0822383373, 9780822383376, 392 pages. DIVThis collection brings new voices and new perspectives to the study of popularвЂ―and particularly rockвЂ―music. Focusing on a variety of artists and music forms, Rock Over the Edge asks what happens to rock criticism when rock is no longer a coherent concept. To work toward an answer, contributors investigate previously neglected genres and styles, such as “lo fi,” alternative country, and “rock en espaГ±ol,” while offering a fresh look at such familiar figures as Elvis Presley, the Beatles, and Kurt Cobain.Bridging the disciplines of musicology and cultural studies, the collection has two primary goals: to seek out a language for talking about music culture and to look at the relationship of music to culture in general. The editors’ introduction provides a backward glance at recent rock criticism and also looks to the future of the rapidly expanding discipline of popular music studies. Taking seriously the implications of critical theory for the study of non-literary aesthetic endeavors, the volume also addresses such issues as the affective power of popular music and the psychic construction of fandom.Rock Over the Edge will appeal to scholars and students in popular music studies and American Studies as well as general readers interested in popular music.Contributors. Ian Balfour, Roger Beebe, Michael Coyle, Robert Fink, Denise Fulbrook, Tony Grajeda, Lawrence Grossberg, Trent Hill, Josh Kun, Jason Middleton, Lisa Ann Parks, Ben Saunders, John J. -

MTV, Media Dan Format Global Kajian Tentang MTV Dan Bangunan Kultur Global
MTV, Media dan Format Global Kajian tentang MTV dan Bangunan Kultur Global Oleh : Liza Diniarizky Putri Fakultas Ilmu Sosial dan Ilmu Politik Universitas Serang Raya Jl. Raya Cilegon, Drangong. Serang – Banten [email protected] ABSTRAK Dampak dari media televisi dan teknologi di dunia membangun sebuah global village, dimana perbedaan waktu dan ruang terkikis akibat sifat instant dari media tersebut. Televisi telah berhasil membuat apa yang terjadi di satu sudut bumi mampu disaksikan di sudut bumi lain dalam waktu yang bersamaan. Percepatan komunikasi seperti ini tentu saja sangat membantu proses globalisasi budaya. MTV adalah salah satu media global paling terkenal dan berhasil menyebarkan budaya. Tulisan ini mencoba mengkaji fenomena budaya global yang dampak dari MTV. Penelitian ini menggunakan metode deskriptif kualitatif. Hasil dari penelitian ini, MTV telah muncul sebagai satu media global, dengan lebih dari 252 juta rumah tangga di 80 negara mengaksesnya. Dalam perjalanannya selama 20 tahun ini, MTV memang telah mengubah budaya dunia. Trend yang berkembang sekarang seperti tidak dapat terlepas dari pengaruh yang ditularkan MTV. Kata kunci: media global, globalisasi I. PENDAHULUAN Kecepatan komunikasi melalui media instant dari media modern dan elektronik menggemakan kecepatan rasa. komunikasi dunia tersebut. Dalam visi ini, Melalui media seperti televisi dan internet, manusia mampu bergabung dalam campuran kita terkait bersama bumi dan ini membuat tempat, kejadian, dan lokasi. Televisi telah kita mampu untuk berhubungan dengan orang- berhasil membuat apa yang terjadi di satu sudut orang dari sisi dunia yang lain secepat kita bumi mampu disaksikan di sudut bumi lain bertemu dan berbicara dengan orang-orang di dalam waktu yang bersamaan. Percepatan sekitar kita. -

Culture Club Announced Alongside Jessica Mauboy, Dami Im and Paul Kelly for 6Th AACTA Awards Presented by Foxtel
MEDIA RELEASE Strictly embargoed until 12.01am on Tuesday 22 November 2016 Culture Club announced alongside Jessica Mauboy, Dami Im and Paul Kelly for 6th AACTA Awards presented by Foxtel In the lead up to Australia’s biggest film and television Awards, the Australian Academy of Cinema and Television Arts (AACTA) has announced that iconic UK pop group Culture Club will be performing at the 6th AACTA Awards presented by Foxtel, alongside Australian artists Paul Kelly, Jessica Mauboy and Dami Im like you’ve never seen her before. Culture Club’s performance at the Awards Ceremony will be their only televised performance and will feature the original band line up: singer Boy George, guitarist and keyboardist Roy Hay, bassist Mikey Craig and drummer Jon Moss. Culture Club are returning to Australia for an Encore Tour in mid- December, which will see them perform in some capital cities and several winery shows. Australia’s love affair with Culture Club continues and their June tour saw them sell out shows and perform to rave reviews. Boy George said he was “Thrilled to be coming back to Australia and to be performing at Australia’s biggest celebration of film and television.” The Grammy Award winning group will bring their own unique style and performance to the AACTA Awards. Selling more than 150 million records worldwide, with multiple worldwide number one singles including Do You Really Want to Hurt Me and the BRIT Award-winning Karma Chameleon, Culture Club are one of the true icons of the world music scene. ARIA Award winning actress and Sony Music recording artist Jessica Mauboy will return to perform at the AACTAs four years since her show-stopping performance at the 2nd AACTA Awards, where she also won the AACTA Award for Best Supporting Actress for her role in THE SAPPHIRES. -
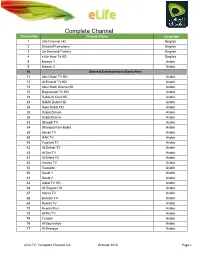
Complete Channel List October 2015 Page 1
Complete Channel Channel No. List Channel Name Language 1 Info Channel HD English 2 Etisalat Promotions English 3 On Demand Trailers English 4 eLife How-To HD English 8 Mosaic 1 Arabic 9 Mosaic 2 Arabic 10 General Entertainment Starts Here 11 Abu Dhabi TV HD Arabic 12 Al Emarat TV HD Arabic 13 Abu Dhabi Drama HD Arabic 15 Baynounah TV HD Arabic 22 Dubai Al Oula HD Arabic 23 SAMA Dubai HD Arabic 24 Noor Dubai HD Arabic 25 Dubai Zaman Arabic 26 Dubai Drama Arabic 33 Sharjah TV Arabic 34 Sharqiya from Kalba Arabic 38 Ajman TV Arabic 39 RAK TV Arabic 40 Fujairah TV Arabic 42 Al Dafrah TV Arabic 43 Al Dar TV Arabic 51 Al Waha TV Arabic 52 Hawas TV Arabic 53 Tawazon Arabic 60 Saudi 1 Arabic 61 Saudi 2 Arabic 63 Qatar TV HD Arabic 64 Al Rayyan HD Arabic 67 Oman TV Arabic 68 Bahrain TV Arabic 69 Kuwait TV Arabic 70 Kuwait Plus Arabic 73 Al Rai TV Arabic 74 Funoon Arabic 76 Al Soumariya Arabic 77 Al Sharqiya Arabic eLife TV : Complete Channel List October 2015 Page 1 Complete Channel 79 LBC Sat List Arabic 80 OTV Arabic 81 LDC Arabic 82 Future TV Arabic 83 Tele Liban Arabic 84 MTV Lebanon Arabic 85 NBN Arabic 86 Al Jadeed Arabic 89 Jordan TV Arabic 91 Palestine Arabic 92 Syria TV Arabic 94 Al Masriya Arabic 95 Al Kahera Wal Nass Arabic 96 Al Kahera Wal Nass +2 Arabic 97 ON TV Arabic 98 ON TV Live Arabic 101 CBC Arabic 102 CBC Extra Arabic 103 CBC Drama Arabic 104 Al Hayat Arabic 105 Al Hayat 2 Arabic 106 Al Hayat Musalsalat Arabic 108 Al Nahar TV Arabic 109 Al Nahar TV +2 Arabic 110 Al Nahar Drama Arabic 112 Sada Al Balad Arabic 113 Sada Al Balad -

Verizon Wireless
Before the FEDERAL COMMUNICATIONS COMMISSION Washington, D.C. 20554 Alex Nguyen, Complainant, v. Proceeding Number 16-242 Bureau ID Number EB-16-MD-003 Cellco Partnership d/b/a Verizon Wireless, Defendants. ANSWER OF CELLCO PARTNERSHIP D/B/A VERIZON WIRELESS TABLE OF CONTENTS SUMMARY .................................................................................................................................... 1 I. PARTIES ............................................................................................................................ 8 II. BACKGROUND ................................................................................................................ 9 A. Answer to Allegations Regarding the C Block Rules and the 2012 Consent Decree ......................................................................................................................9 B. Answer to Allegations Regarding the 2015 Open Internet Order .........................15 C. Answer to Allegations that Device Providers Support LTE Band 13 for Compatibility with the Verizon Wireless Network ...............................................16 D. Answer to Allegations Regarding Verizon’s Device Sales ...................................16 E. Answer to Allegations Regarding Verizon’s Device Certification Process ..........17 F. Answer to Allegations Regarding the Length of Verizon’s Device Certification Process ..............................................................................................20 III. ANSWER TO ALLEGATIONS THAT VERIZON INTERFERES -

Music Video P R O G R a M M I N G New Media Get Decidedly Mixed Reviews; New York Cable Backs out of the Box
Music Video P R O G R A M M I N G New Media Get Decidedly Mixed Reviews; New York Cable Backs Out Of The Box GLITCHES: 1995 will probably be allowed the computer -owning viewer a U.K. operations was snapped up by a remembered as the year in which new chance to critique videos as they played subsidiary of Ticketmaster. media aggressively forced its way into on the music channel. However, the Box will find itself the music video industry. Ask any music Some other music video programmers unplugged in its largest market at the video veteran about this sudden intru- found the transition from television to beginning of 1996. New York's Time sion and the response is likely to be one Warner Cable is replacing the music of either excitement or utter despair. video channel with the History Channel, Many members of the production 1995 IN REVIEW effective Jan. 2. industry hope to benefit from the busi- Time Warner Cable's New York reach ness opportunities of new media, as they includes more than a million customers begin to branch out their services to help computer to be-e1 umm bit buggy. in -a Manhattan, Brooklyn, and Queens. We Two Are One. VH1 demonstrated its commitment to original music program- produce content for CD -ROMs. The Box's plans to "cybercast" its pro- Significantly, the corporate offices of the ming with the debut of "Duets" in 1995. Pictured in the first installment of the per- In addition, some record label music gramming on the Internet's World Wide New York -based major music labels will formance series, from left, are Joan Osborne and Melissa Etheridge. -

THE GLOBALIZATION of K-POP by Gyu Tag
DE-NATIONALIZATION AND RE-NATIONALIZATION OF CULTURE: THE GLOBALIZATION OF K-POP by Gyu Tag Lee A Dissertation Submitted to the Graduate Faculty of George Mason University in Partial Fulfillment of The Requirements for the Degree of Doctor of Philosophy Cultural Studies Committee: ___________________________________________ Director ___________________________________________ ___________________________________________ ___________________________________________ Program Director ___________________________________________ Dean, College of Humanities and Social Sciences Date: _____________________________________ Spring Semester 2013 George Mason University Fairfax, VA De-Nationalization and Re-Nationalization of Culture: The Globalization of K-Pop A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy at George Mason University By Gyu Tag Lee Master of Arts Seoul National University, 2007 Director: Paul Smith, Professor Department of Cultural Studies Spring Semester 2013 George Mason University Fairfax, VA Copyright 2013 Gyu Tag Lee All Rights Reserved ii DEDICATION This is dedicated to my wife, Eunjoo Lee, my little daughter, Hemin Lee, and my parents, Sung-Sook Choi and Jong-Yeol Lee, who have always been supported me with all their hearts. iii ACKNOWLEDGEMENTS This dissertation cannot be written without a number of people who helped me at the right moment when I needed them. Professors, friends, colleagues, and family all supported me and believed me doing this project. Without them, this dissertation is hardly can be done. Above all, I would like to thank my dissertation committee for their help throughout this process. I owe my deepest gratitude to Dr. Paul Smith. Despite all my immaturity, he has been an excellent director since my first year of the Cultural Studies program. -

India's Edgiest Comedy Collective
INDIA’S EDGIEST COMEDY COLLECTIVE AUSTRALIAN TOUR 2016 MELBOURNE THE FORUM FRIDAY 6 MAY Book at Ticketmaster 136 100 www.ticketmaster.com.au SYDNEY ENMORE THEATRE SUNDAY 8 MAY Book at Festival Box Office 9020 6966 www.sydneycomedyfest.com.au or Ticketek 132 849 www.ticketek.com.au TICKETS ON SALE NOW All IndiA BAkchod (AIB) is India's edgiest, most infamous comedy collective. They are the biggest selling stand-up ACt in India and are famous for sketches released on their wildly popular YouTube chAnnel with over 1.4 million subscribers. They executed India's first celebrity roast in 2015, the video for which garnered 11 million views in 3 days. Apart from performing all across India, they have toured their irreverent brand of comedy in Singapore and Dubai. This will be their first tour of Australia. The 60-minute show will feature stand-up, songs and sketches. TAnmAy BhAt, GursimrAn KhAmbA, Rohan Joshi and Ashish ShAkyA, AIB are widely regarded as India’s premier comedic tour-de-force across multiple forms of media. Gursimran is the co-founder of AIB and has been a standup comic since 2009. He enjoys talking about things people don't like talking about. “Perhaps the most outrageous comic” Deccan Herald. Tanmay Bhat is one of India’s brightest comedians. He is also a television writer and feature film writer, humour columnist with First Post and Time Out MumbAi. His television credits include India’s first English sketch comedy special Ripping The DeCAde on StAr World. “Tanmay is such an exciting tAlent thAt you need more thAn just your hAnds to clAp for him. -

Korea Wave Foundation
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by SOAS Research Online The Foundations Of Hallyu – K-Pop’s Coming Of Age Keith Howard We are, collectively, still struggling to come to terms with Hallyu, Korean Wave. This is seen in the multitude of contrasting perspectives that have been applied by journalists and academics alike since the turn of the new millennium. There is a lack of consensus, and perspectives run from fear and criticism by what Cho Hae-joang calls the postcolonial camp, through pride and celebration in what is happening (Cho’s nationalist camp), to economic planning (the neoliberal camp; Cho Hae-joang 2005).1 The three camps seem to trend chronologically in the order given here,2 but are no longer sufficient now that Korean Wave has spread to the world beyond Asia. Indeed, recent foreign commentaries about the economy of Korean Wave have diverged, often markedly, from Korean accounts of its global popularity. New models are needed, one of which, Ingyu Oh and Gil-Sung Park’s supply chain model (2012), seems to have considerable utility.3 Their theory throws out existing, albeit dated, accounts of the music industry, and demonstrates how the internationalization of Korean Wave moves the industry from a fan-oriented service business (B2C) to business servicing (B2B). Our accounts do, though, agree on key moments in Korean Wave: 1999, when the term, hallyu, began to be used; 2003 when “Winter Sonata” reached Japan; 2008 or shortly after when Korean pop again moved into a global frame; and 2012 as the date when Psy conquered YouTube. -

The VIP-Booking European Live Entertainment Book Advertising in the VIP Book Will Make You Visible to 10.000 Business Professionals All Over Europe
WWW.VIP-BOOKING.coM VIP- News›› ›› PREmiUM VOL. 137 JUNE 2011 McGowan’s Musings: So there I was, crossing a wide and fast collectively known, strangely enough, as flowing river on bridge that looked per- Music Festivals. Encouraged by a Hop Farm fectly solid from the river bank but began sell-out with Prince, extending this year’s to sway from side to side in a strangely edition in July by a day, Power has filed the disturbing fashion when supporting the application for Music Festival’s admission weight of a man in full Scottish highland to Aim, the London Stock Exchange’s inter- dress playing the bagpipes and being national market for smaller growing com- followed by a trail of music industry folk panies, which will raise £6.5m. (See Busi- looking forward to the first drink of the ness News in this issue) Although there are evening. I was however temporarily dis- some worries being expressed about the tracted from concerns about the stability fortunes of many of this season’s events Allan McGowan of the bridge by the sight of the man up to with Reading tickets selling for less than his chest in the centre of this rushing river face value on the secondary market and unconcernedly wielding a very substantial Music and Arts Festival in Manchester, audiences being spread thin by a combi- fishing rod and also wearing a highland Tennessee, temperatures stayed in the 90s nation of a lack on new acts on the bills ‘bunnet’ while he attempted to catch fish (F), 30s (C) for almost the whole four days and increased competition (there were on their way to the one and only Loch Ness.