Chapter 3 Consumer Behavior
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
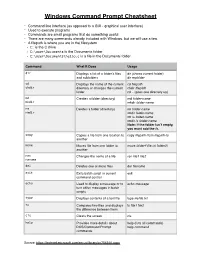
Windows Command Prompt Cheatsheet
Windows Command Prompt Cheatsheet - Command line interface (as opposed to a GUI - graphical user interface) - Used to execute programs - Commands are small programs that do something useful - There are many commands already included with Windows, but we will use a few. - A filepath is where you are in the filesystem • C: is the C drive • C:\user\Documents is the Documents folder • C:\user\Documents\hello.c is a file in the Documents folder Command What it Does Usage dir Displays a list of a folder’s files dir (shows current folder) and subfolders dir myfolder cd Displays the name of the current cd filepath chdir directory or changes the current chdir filepath folder. cd .. (goes one directory up) md Creates a folder (directory) md folder-name mkdir mkdir folder-name rm Deletes a folder (directory) rm folder-name rmdir rmdir folder-name rm /s folder-name rmdir /s folder-name Note: if the folder isn’t empty, you must add the /s. copy Copies a file from one location to copy filepath-from filepath-to another move Moves file from one folder to move folder1\file.txt folder2\ another ren Changes the name of a file ren file1 file2 rename del Deletes one or more files del filename exit Exits batch script or current exit command control echo Used to display a message or to echo message turn off/on messages in batch scripts type Displays contents of a text file type myfile.txt fc Compares two files and displays fc file1 file2 the difference between them cls Clears the screen cls help Provides more details about help (lists all commands) DOS/Command Prompt help command commands Source: https://technet.microsoft.com/en-us/library/cc754340.aspx. -

Mac Keyboard Shortcuts Cut, Copy, Paste, and Other Common Shortcuts
Mac keyboard shortcuts By pressing a combination of keys, you can do things that normally need a mouse, trackpad, or other input device. To use a keyboard shortcut, hold down one or more modifier keys while pressing the last key of the shortcut. For example, to use the shortcut Command-C (copy), hold down Command, press C, then release both keys. Mac menus and keyboards often use symbols for certain keys, including the modifier keys: Command ⌘ Option ⌥ Caps Lock ⇪ Shift ⇧ Control ⌃ Fn If you're using a keyboard made for Windows PCs, use the Alt key instead of Option, and the Windows logo key instead of Command. Some Mac keyboards and shortcuts use special keys in the top row, which include icons for volume, display brightness, and other functions. Press the icon key to perform that function, or combine it with the Fn key to use it as an F1, F2, F3, or other standard function key. To learn more shortcuts, check the menus of the app you're using. Every app can have its own shortcuts, and shortcuts that work in one app may not work in another. Cut, copy, paste, and other common shortcuts Shortcut Description Command-X Cut: Remove the selected item and copy it to the Clipboard. Command-C Copy the selected item to the Clipboard. This also works for files in the Finder. Command-V Paste the contents of the Clipboard into the current document or app. This also works for files in the Finder. Command-Z Undo the previous command. You can then press Command-Shift-Z to Redo, reversing the undo command. -
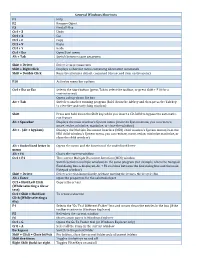
General Windows Shortcuts
General Windows Shortcuts F1 Help F2 Rename Object F3 Find all files Ctrl + Z Undo Ctrl + X Cut Ctrl + C Copy Ctrl + V Paste Ctrl + Y Redo Ctrl + Esc Open Start menu Alt + Tab Switch between open programs Alt + F4 Quit program Shift + Delete Delete item permanently Shift + Right Click Displays a shortcut menu containing alternative commands Shift + Double Click Runs the alternate default command ( the second item on the menu) Alt + Double Click Displays properties F10 Activates menu bar options Shift + F10 Opens a contex t menu ( same as righ t click) Ctrl + Esc or Esc Selects the Start button (press Tab to select the taskbar, or press Shift + F10 for a context menu) Alt + Down Arrow Opens a drop‐down list box Alt + Tab Switch to another running program (hold down the Alt key and then press the Tab key to view the task‐switching window) Alt + Shift + Tab Swit ch b ackward s b etween open appli cati ons Shift Press and hold down the Shift key while you insert a CD‐ROM to bypass the automatic‐ run feature Alt + Spacebar Displays the main window's System menu (from the System menu, you can restore, move, resize, minimize, maximize, or close the window) Alt + (Alt + hyphen) Displays the Multiple Document Interface (MDI) child window's System menu (from the MDI child window's System menu, you can restore, move, resize, minimize maximize, or close the child window) Ctrl + Tab Switch to t h e next child window o f a Multi ple D ocument Interf ace (MDI) pr ogram Alt + Underlined letter in Opens the menu and the function of the underlined letter -

Lecture 4 " Theory of Choice and Individual Demand
Lecture 4 - Theory of Choice and Individual Demand David Autor 14.03 Fall 2004 Agenda 1. Utility maximization 2. Indirect Utility function 3. Application: Gift giving –Waldfogel paper 4. Expenditure function 5. Relationship between Expenditure function and Indirect utility function 6. Demand functions 7. Application: Food stamps –Whitmore paper 8. Income and substitution e¤ects 9. Normal and inferior goods 10. Compensated and uncompensated demand (Hicksian, Marshallian) 11. Application: Gi¤en goods –Jensen and Miller paper Roadmap: 1 Axioms of consumer preference Primal Dual Max U(x,y) Min pxx+ pyy s.t. pxx+ pyy < I s.t. U(x,y) > U Indirect Utility function Expenditure function E*= E(p , p , U) U*= V(px, py, I) x y Marshallian demand Hicksian demand X = d (p , p , I) = x x y X = hx(px, py, U) = (by Roy’s identity) (by Shepard’s lemma) ¶V / ¶p ¶ E - x - ¶V / ¶I Slutsky equation ¶p x 1 Theory of consumer choice 1.1 Utility maximization subject to budget constraint Ingredients: Utility function (preferences) Budget constraint Price vector Consumer’sproblem Maximize utility subjet to budget constraint Characteristics of solution: Budget exhaustion (non-satiation) For most solutions: psychic tradeo¤ = monetary payo¤ Psychic tradeo¤ is MRS Monetary tradeo¤ is the price ratio 2 From a visual point of view utility maximization corresponds to the following point: (Note that the slope of the budget set is equal to px ) py Graph 35 y IC3 IC2 IC1 B C A D x What’swrong with some of these points? We can see that A P B, A I D, C P A. -

Powerview Command Reference
PowerView Command Reference TRACE32 Online Help TRACE32 Directory TRACE32 Index TRACE32 Documents ...................................................................................................................... PowerView User Interface ............................................................................................................ PowerView Command Reference .............................................................................................1 History ...................................................................................................................................... 12 ABORT ...................................................................................................................................... 13 ABORT Abort driver program 13 AREA ........................................................................................................................................ 14 AREA Message windows 14 AREA.CLEAR Clear area 15 AREA.CLOSE Close output file 15 AREA.Create Create or modify message area 16 AREA.Delete Delete message area 17 AREA.List Display a detailed list off all message areas 18 AREA.OPEN Open output file 20 AREA.PIPE Redirect area to stdout 21 AREA.RESet Reset areas 21 AREA.SAVE Save AREA window contents to file 21 AREA.Select Select area 22 AREA.STDERR Redirect area to stderr 23 AREA.STDOUT Redirect area to stdout 23 AREA.view Display message area in AREA window 24 AutoSTOre .............................................................................................................................. -

S.Ha.R.K. Installation Howto Tools Knoppix Live CD Linux Fdisk HD
S.Ha.R.K. Installation Tools HowTo • Linux fdisk utility • A copy of Linux installation CD • A copy of Windows® installation CD Tullio Facchinetti University of Pavia - Italy • Some FreeDOS utilities • A copy of S.Ha.R.K. S.Ha.R.K. Workshop S.Ha.R.K. Workshop Knoppix live CD Linux fdisk Command action a toggle a bootable flag Download ISO from b edit bsd disklabel c toggle the dos compatibility flag d delete a partition http://www.knoppix.org l list known partition types m print this menu n add a new partition o create a new empty DOS partition table p print the partition table q quit without saving changes • boot from CD s create a new empty Sun disklabel t change a partition's system id • open a command shell u change display/entry units v verify the partition table • type “su” (become root ), password is empty w write table to disk and exit x extra functionality (experts only) • start fdisk (ex. fdisk /dev/hda ) Command (m for help): S.Ha.R.K. Workshop S.Ha.R.K. Workshop HD partitioning HD partitioning 1st FreeDOS FAT32 FreeDOS must be installed Primary 2nd Windows® FAT32 into the first partition of your HD or it may not boot 3rd Linux / extX Data 1 FAT32 format data partitions as ... Extended FAT32, so that you can share Data n FAT32 your data between Linux, last Linux swap swap Windows® and FreeDOS S.Ha.R.K. Workshop S.Ha.R.K. Workshop 1 HD partitioning Windows ® installation FAT32 Windows® partition type Install Windows®.. -

2. Budget Constraint.Pdf
Engineering Economic Analysis 2019 SPRING Prof. D. J. LEE, SNU Chap. 2 BUDGET CONSTRAINT Consumption Choice Sets . A consumption choice set, X, is the collection of all consumption choices available to the consumer. n X = R+ . A consumption bundle, x, containing x1 units of commodity 1, x2 units of commodity 2 and so on up to xn units of commodity n is denoted by the vector xx =(1 ,..., xn ) ∈ X n . Commodity price vector pp =(1 ,..., pn ) ∈R+ 1 Budget Constraints . Q: When is a bundle (x1, … , xn) affordable at prices p1, … , pn? • A: When p1x1 + … + pnxn ≤ m where m is the consumer’s (disposable) income. The consumer’s budget set is the set of all affordable bundles; B(p1, … , pn, m) = { (x1, … , xn) | x1 ≥ 0, … , xn ≥ 0 and p1x1 + … + pnxn ≤ m } . The budget constraint is the upper boundary of the budget set. p1x1 + … + pnxn = m 2 Budget Set and Constraint for Two Commodities x2 Budget constraint is m /p2 p1x1 + p2x2 = m. m /p1 x1 3 Budget Set and Constraint for Two Commodities x2 Budget constraint is m /p2 p1x1 + p2x2 = m. the collection of all affordable bundles. Budget p1x1 + p2x2 ≤ m. Set m /p1 x1 4 Budget Constraint for Three Commodities • If n = 3 x2 p1x1 + p2x2 + p3x3 = m m /p2 m /p3 x3 m /p1 x1 5 Budget Set for Three Commodities x 2 { (x1,x2,x3) | x1 ≥ 0, x2 ≥ 0, x3 ≥ 0 and m /p2 p1x1 + p2x2 + p3x3 ≤ m} m /p3 x3 m /p1 x1 6 Opportunity cost in Budget Constraints x2 p1x1 + p2x2 = m Slope is -p1/p2 a2 Opp. -

KEYBOARD SHORTCUTS (Windows)
KEYBOARD SHORTCUTS (Windows) Note: For Mac users, please substitute the Command key for the Ctrl key. This substitution with work for the majority of commands _______________________________________________________________________ General Commands Navigation Windows key + D Desktop to foreground Context menu Right click Alt + underlined letter Menu drop down, Action selection Alt + Tab Toggle between open applications Alt, F + X or Alt + F4 Exit application Alt, Spacebar + X Maximize window Alt, Spacebar + N Minimize window Ctrl + W Closes window F2 Renames a selected file or folder Open Programs To open programs from START menu: Create a program shortcut and drop it into START menu To open programs/files on Desktop: Select first letter, and then press Enter to open Dialog Boxes Enter Selects highlighted button Tab Selects next button Arrow keys Selects next (>) or previous button (<) Shift + Tab Selects previous button _______________________________________________________________________ Microsoft Word Formatting Ctrl + P Print Ctrl + S Save Ctrl + Z Undo Ctrl + Y Redo CTRL+B Make text bold CTRL+I Italicize CTRL+U Underline Ctrl + C Copy Ctrl + V Paste Ctrl + X Copy + delete Shift + F3 Change case of letters Ctrl+Shift+> Increase font size Ctrl+Shift+< Decrease font size Highlight Text Shift + Arrow Keys Selects one letter at a time Shift + Ctrl + Arrow keys Selects one word at a time Shift + End or Home Selects lines of text Change or resize the font CTRL+SHIFT+ > Increase the font size 1 KEYBOARD SHORTCUTS (Windows) CTRL+SHIFT+ < -

Package 'Move'
Package ‘move’ November 26, 2020 Type Package Title Visualizing and Analyzing Animal Track Data Version 4.0.6 Description Contains functions to access movement data stored in 'movebank.org' as well as tools to visualize and statistically analyze animal movement data, among others functions to calculate dynamic Brownian Bridge Movement Models. Move helps addressing movement ecology questions. License GPL (>= 3) URL https://bartk.gitlab.io/move/ BugReports https://gitlab.com/bartk/move/-/issues LazyLoad yes LazyData yes LazyDataCompression xz Depends geosphere (>= 1.4-3), methods, sp, raster (>= 2.4-15), rgdal, R (>= 3.5.0) Suggests adehabitatHR, adehabitatLT, markdown, rmarkdown, circular, ggmap, mapproj, maptools, testthat, knitr, ggplot2, leaflet, lubridate, ctmm, amt, bcpa, EMbC Imports httr, memoise, xml2, Rcpp LinkingTo Rcpp SystemRequirements C++11 RoxygenNote 7.1.1 VignetteBuilder knitr NeedsCompilation yes Author Bart Kranstauber [aut, cre], Marco Smolla [aut], Anne K Scharf [aut] Maintainer Bart Kranstauber <[email protected]> Repository CRAN Date/Publication 2020-11-26 15:50:06 UTC 1 2 R topics documented: R topics documented: move-package . .3 .UD-class . .5 .unUsedRecords-class . .6 angle . .7 as.data.frame . .8 brownian.bridge.dyn . 10 brownian.motion.variance.dyn . 13 burst............................................. 14 burstId . 15 citations . 16 contour . 17 coordinates . 18 corridor . 18 DBBMM-class . 20 DBBMMBurstStack-class . 22 DBBMMStack-class . 23 dBGBvariance-class . 24 dBMvariance . 25 distance . 26 duplicatedDataExample . 27 dynBGB . 28 dynBGB-class . 30 dynBGBvariance . 31 emd ............................................. 33 equalProj . 35 fishers . 36 getDataRepositoryData . 36 getDuplicatedTimestamps . 37 getMotionVariance . 39 getMovebank . 40 getMovebankAnimals . 43 getMovebankData . 44 getMovebankID . 47 getMovebankLocationData . 48 getMovebankNonLocationData . 51 getMovebankReferenceTable . 53 getMovebankSensors . 54 getMovebankSensorsAttributes . 55 getMovebankStudies . -

3 Lecture 3: Choices from Budget Sets
3 Lecture 3: Choices from Budget Sets Up to now, we have been rather demanding about the data that we need in order to test our models. We have made two important assumptions: that we observe choices from all possible choice sets, and that we observe choice correspondences (i.e. we see all the options that a decision maker would be ‘happy with’). In many cases, we may not be so lucky with our data. Unfortunately, without these two properties, conditions and are no longer necessary or sufficient to guarantee a utility representation. Consider the following example of an incomplete data set. Example 1 Let = and say we observe the following (incomplete) choice correspondence { } ( )= { } { } ( )= { } { } ( )= { } { } This choice correspondence satisfies properties and trivially. is satisfied because we do not observe any choices from sets that are subsets of each other. is satisfied because we never see two objects chosen from the same set. However, there is no way that we can rationalize these choices with a complete preference relation. The first observation implies that ,thesecond  that and the third that 3. Thus, any binary relation that would rationalize these choices   would be intransitive. In fact, in order for theorem 1 to hold, we don’t have to observe choices from all subsets of , but we do have to need at least all subsets of that contain two and three elements (you should go back and look at the proof of theorem 1 and check that you agree with this statement). What about if we drop the assumption that we observe a choice correspondence, and instead observe a choice function? For example, we could ask the following question: Question 1 Let :2 ∅ be a choice function. -

EC9D3 Advanced Microeconomics, Part I: Lecture 2
EC9D3 Advanced Microeconomics, Part I: Lecture 2 Francesco Squintani August, 2020 Budget Set Up to now we focused on how to represent the consumer's preferences. We shall now consider the sour note of the constraint that is imposed on such preferences. Definition (Budget Set) The consumer's budget set is: B(p; m) = fx j (p x) ≤ m; x 2 X g Francesco Squintani EC9D3 Advanced Microeconomics, Part I August, 2020 2 / 49 Budget Set (2) 6 x1 2 L = 2 X = R+ c c c c c c c c c c c c B(p; m) c c c c c c c - x2 Francesco Squintani EC9D3 Advanced Microeconomics, Part I August, 2020 3 / 49 Income and Prices The two exogenous variables that characterize the consumer's budget set are: the level of income m the vector of prices p = (p1;:::; pL). Often the budget set is characterized by a level of income represented by the value of the consumer's endowment x0 (labour supply): m = (p x0) Francesco Squintani EC9D3 Advanced Microeconomics, Part I August, 2020 4 / 49 Utility Maximization The basic consumer's problem (with rational, continuous and monotonic preferences): max u(x) fxg s:t: x 2 B(p; m) Result If p > 0 and u(·) is continuous, then the utility maximization problem has a solution. Proof: If p > 0 (i.e. pl > 0, 8l = 1;:::; L) the budget set is compact (closed, bounded) hence by Weierstrass theorem the maximization of a continuous function on a compact set has a solution. Francesco Squintani EC9D3 Advanced Microeconomics, Part I August, 2020 5 / 49 First Order Condition Result If u(·) is continuously differentiable, the solution x∗ = x(p; m) to the consumer's problem is characterized by the following necessary conditions. -

Disk Management
IBM i Version 7.2 Systems management Disk management IBM Note Before using this information and the product it supports, read the information in “Notices” on page 141. This edition applies to IBM i 7.2 (product number 5770-SS1) and to all subsequent releases and modifications until otherwise indicated in new editions. This version does not run on all reduced instruction set computer (RISC) models nor does it run on CISC models. This document may contain references to Licensed Internal Code. Licensed Internal Code is Machine Code and is licensed to you under the terms of the IBM License Agreement for Machine Code. © Copyright International Business Machines Corporation 2004, 2013. US Government Users Restricted Rights – Use, duplication or disclosure restricted by GSA ADP Schedule Contract with IBM Corp. Contents Disk management..................................................................................................1 What's new for IBM i 7.2..............................................................................................................................1 PDF file for Disk Management..................................................................................................................... 1 Getting started with disk management.......................................................................................................2 Components of disk storage.................................................................................................................. 2 Finding the logical address for a disk