DOCSLIB.ORG

The Triangular Number Is a Polygonal Number - a Number That Can Be Represented by a Regular Geometric Arrangement of Equally Spaced Points

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Triangular Number Is a Polygonal Number - a Number That Can Be Represented by a Regular Geometric Arrangement of Equally Spaced Points The triangular number is a polygonal number - a number that can be represented by a regular geometric arrangement of equally spaced points. As the name suggests, triangular numbers can be visualized as a triangle of points. The triangular numbers can be found in the third diagonal of Pascal`s triangle, starting at row 3. The first triangular number is 1, the second is 3, the third is 6, the fourth is 10, and so on. Triangular numbers can be calculated by adding up consecutive numbers. Here are 5 different ways to develop (and prove) the formula for the sum of the first n natural numbers: T(n) = 1 + 2 + 3 + 4 + . + n Method 1: Using Differences The following table shows the sum of some natural numbers. n 0 1 2 3 4 5 Sn 0 1 3 6 10 15 Δ1 2 3 4 5 Δ2 1 1 1 1 Sn is the sum of the numbers to n. Because we find that the second difference Δ2 produces constant values, we assume the formula for the sum of the natural numbers is a quadratic, of the form an2+bn+c. Using our values, we substitute 0, 1, and 3 in the Equation: n Equation Equation Number 0 c=0 1 1 a+b=1 2 2 4a+2b=3 3 Note in Equations 2 and 3 that c=0. By subtracting twice Equation 2 from Equation 3, we get 2a=1, So a=1/2 Substituting the value for a in Equation 2, we find that b is also 1/2, So the sum of the first n natural numbers is Method 2: Using Gauss Let us write the sum of the natural numbers up to n in two ways as: Sn=1+2+3+...+(n-2)+(n-1)+n and Sn =n+(n-1)+(n-2)+...+3+2+1. If we add these two series we get: 2Sn=(n+1)+(n+1)+...+(n+1). There are n of these (n+1)'s so 2Sn=n(n+1) therefore Sn=(n(n+1))/2. Method 3: Using Summation Note that the sum of the squares of the first n natural numbers is the sum of the first (n+1) minus (n+1)2. Expanding the (k+1)th term: Expanding (n+1)2, and rounding up similar terms: Which gives us the sum of the first n natural numbers: Method 4: By Finding a General Term Note the difference between the sum of the first n natural numbers, and the sum to (n-1) is n: Sn – S(n-1) = n. Write down the known differences, hoping that a pattern appears and write Sn-k, and then write down the nth term, from which a formula can be extracted. A pattern becomes clear. In general, the kth term: Note that the "n" term is always kn, and the other term is a sum of the natural numbers. Make k=n, and so get the nth term, noting S0=0. The sum above is one n short of Sn: Substituting , → And finally, . Method 5: Using a Visual Model We can visualize the sum 1+2+3+...+n as a triangle of dots. Numbers which have such a pattern of dots are called Triangle (or triangular) numbers, written T(n), the sum of the integers from 1 to n : n 1 2 3 4 5 6 T(n) as a sum 1 1+2 1+2+3 1+2+3+4 1..5 1..6 T(n) as a triangle ... T(n)= 1 3 6 10 15 21 For the proof, we will count the number of dots in T(n) but, instead of summing the numbers 1, 2, 3, etc up to n we will find the total using only one multiplication and one division! To do this, we will fit two copies of a triangle of dots together, one red and an upside-down copy in green. E.g. T(4)=1+2+3+4 + = Notice that we get a rectangle which is has the same number of rows (4) but has one extra column (5). So the rectangle is 4 by 5. It therefore contains 4x5=20 balls, but we took two copies of T(4) to get this. So we must have 20/2 = 10 balls in T(4), which we can easily check. This visual proof applies to any size of triangle number. Here it is again on T(5): + = So T(5) is half of a rectangle of dots 5 tall and 6 wide, i.e. half of 30 dots, so T(5)=15. References: http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/runsums/triNbProof.html http://www.trans4mind.com/personal_development/mathematics/series/sumNatural Numbers.htm http://people.bath.ac.uk/sjb37/pascals-triangle-2.gif http://www.puzzles.com/puzzlesineducation/HandsOnPuzzles/TriangularNumbers/ TriangularNumbers.gif .
Load more

Recommended publications
  • Special Kinds of Numbers
    Chapel Hill Math Circle: Special Kinds of Numbers 11/4/2017 1 Introduction This worksheet is concerned with three classes of special numbers: the polyg- onal numbers, the Catalan numbers, and the Lucas numbers. Polygonal numbers are a nice geometric generalization of perfect square integers, Cata- lan numbers are important numbers that (one way or another) show up in a wide variety of combinatorial and non-combinatorial situations, and Lucas numbers are a slight twist on our familiar Fibonacci numbers. The purpose of this worksheet is not to give an exhaustive treatment of any of these numbers, since that is just not possible. The goal is to, instead, introduce these interesting classes of numbers and give some motivation to explore on your own. 2 Polygonal Numbers The first class of numbers we'll consider are called polygonal numbers. We'll start with some simpler cases, and then derive a general formula. Take 3 points and arrange them as an equilateral triangle with side lengths of 2. Here, I use the term \side-length" to mean \how many points are in a side." The total number of points in this triangle (3) is the second triangular number, denoted P (3; 2). To get the third triangular number P (3; 3), we take the last configuration and adjoin points so that the outermost shape is an equilateral triangle with a side-length of 3. To do this, we can add 3 points along any one of the edges. Since there are 3 points in the original 1 triangle, and we added 3 points to get the next triangle, the total number of points in this step is P (3; 3) = 3 + 3 = 6.
    [Show full text]
  • 10901 Little Patuxent Parkway Columbia, MD 21044
    10901 Little Patuxent Parkway Columbia, MD 21044 Volume 1 | 2018 We would like to thank The Kalhert Foundation for their support of our students and specifically for this journal. Polygonal Numbers and Common Differences Siavash Aarabi, Howard Community College 2017, University of Southern California Mentored by: Mike Long, Ed.D & Loretta FitzGerald Tokoly, Ph.D. Abstract The polygonal numbers, or lattices of objects arranged in polygonal shapes, are more than just geometric shapes. The lattices for a polygon with a certain number of sides represent the polygon where the sides increase from length 1, then 2, then 3 and so forth. The mathematical richness emerges when the number of objects in each lattice is counted for the polygons of increasing larger size and then analyzed. So where are the differences? The polygonal numbers being considered in this project represent polygons that have different numbers of sides. It is when the integer powers of the polygonal sequence for a polygon with a specific number of sides are computed and their differences computed, some interesting commonalities emerge. That there are mathematical patterns in the commonalities that arise from differences are both unexpected and pleasing. Background A polygonal number is a number represented as dots or pebbles arranged in the shape of a regular polygon, or a polygon where the lengths of all sides are congruent. Consider a triangle as one polygon, and then fill the shape up according to figure 1, the sequence of numbers will form Triangular Numbers. The nth Triangular Numbers is also known as the sum of the first n positive integers.
    [Show full text]
  • Triangular Numbers /, 3,6, 10, 15, ", Tn,'" »*"
    TRIANGULAR NUMBERS V.E. HOGGATT, JR., and IVIARJORIE BICKWELL San Jose State University, San Jose, California 9111112 1. INTRODUCTION To Fibonacci is attributed the arithmetic triangle of odd numbers, in which the nth row has n entries, the cen- ter element is n* for even /?, and the row sum is n3. (See Stanley Bezuszka [11].) FIBONACCI'S TRIANGLE SUMS / 1 =:1 3 3 5 8 = 2s 7 9 11 27 = 33 13 15 17 19 64 = 4$ 21 23 25 27 29 125 = 5s We wish to derive some results here concerning the triangular numbers /, 3,6, 10, 15, ", Tn,'" »*". If one o b - serves how they are defined geometrically, 1 3 6 10 • - one easily sees that (1.1) Tn - 1+2+3 + .- +n = n(n±M and (1.2) • Tn+1 = Tn+(n+1) . By noticing that two adjacent arrays form a square, such as 3 + 6 = 9 '.'.?. we are led to 2 (1.3) n = Tn + Tn„7 , which can be verified using (1.1). This also provides an identity for triangular numbers in terms of subscripts which are also triangular numbers, T =T + T (1-4) n Tn Tn-1 • Since every odd number is the difference of two consecutive squares, it is informative to rewrite Fibonacci's tri- angle of odd numbers: 221 222 TRIANGULAR NUMBERS [OCT. FIBONACCI'S TRIANGLE SUMS f^-O2) Tf-T* (2* -I2) (32-22) Ti-Tf (42-32) (52-42) (62-52) Ti-Tl•2 (72-62) (82-72) (9*-82) (Kp-92) Tl-Tl Upon comparing with the first array, it would appear that the difference of the squares of two consecutive tri- angular numbers is a perfect cube.
    [Show full text]
  • On Some Polynomial Values of Repdigit Numbers
    ON SOME POLYNOMIAL VALUES OF REPDIGIT NUMBERS T. KOVACS,´ GY. PETER,´ N. VARGA (DEBRECEN) Abstract. We study the equal values of repdigit numbers and the k dimensional polygonal numbers. We state some effective finiteness theorems, and for small parameter values we completely solve the corresponding equations. Let x(x + 1) ··· (x + k − 2)((m − 2)x + k + 2 − m) (1) f (x) = k;m k! be the mth order k dimensional polygonal number, where k ≥ 2 and m ≥ 3 are fixed integers. As special cases for fk;3 we get the bi- x+k−1 nomial coefficient k , for f2;m(x) and f3;m(x) we have the corre- sponding polygonal and pyramidal numbers, respectively. These fig- urate numbers have already been investigated from several aspects and therefore have a rich literature, see Dickson [9]. For example, the question whether a perfect square is a binomial coefficient, i.e., if fk;3(x) = f2;4(y) and also the more general question on the power val- ues of binomial coefficients was resolved by Gy}ory[12]. The equation x y n = 2 has been investigated by several authors, for general effective finiteness statements we refer to Kiss [17] and Brindza [6]. In the spe- cial cases m = 3; 4; 5 and 6, the corresponding diophantine equations were resolved by Avanesov [1], Pint´er[19] and de Weger [23] (inde- pendently), Bugeaud, Mignotte, Stoll, Siksek, Tengely [8] and Hajdu, Pint´er[13], respectively. The equal values of polygonal and pyrami- dal numbers were studied by Brindza, Pint´er,Turj´anyi [7] and Pint´er, Varga [20].
    [Show full text]
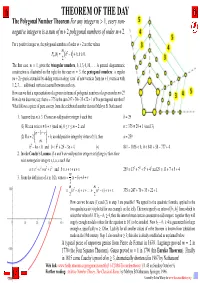
  • The Polygonal Number Theorem for Any Integer M > 1, Every Non- Negative Integer N Is a Sum of M+2 Polygonal Numbers of Order M+2
    THEOREM OF THE DAY The Polygonal Number Theorem For any integer m > 1, every non- negative integer n is a sum of m+2 polygonal numbers of order m+2. For a positive integer m, the polygonal numbers of order m + 2 are the values m P (k) = k2 − k + k, k ≥ 0. m 2 The first case, m = 1, gives the triangular numbers, 0, 1, 3, 6, 10,.... A general diagrammatic construction is illustrated on the right for the case m = 3, the pentagonal numbers: a regular (m + 2)−gon is extended by adding vertices along ‘rays’ of new vertices from (m + 1) vertices with 1, 2, 3,... additional vertices inserted between each ray. How can we find a representation of a given n in terms of polygonal numbers of a given order m+2? How do we discover, say, that n = 375 is the sum 247+70+35+22+1 of five pentagonal numbers? What follows a piece of pure sorcery from the celebrated number theorist Melvyn B. Nathanson! 1. Assume that m ≥ 3. Choose an odd positive integer b such that b = 29 (1) We can write n ≡ b + r (mod m), 0 ≤ r ≤ m − 2; and n = 375 ≡ 29 + 1 (mod 3) n − b − r (2) If a = 2 + b, an odd positive integer by virtue of (1), then a = 259 m ! b2 − 4a < 0 and 0 < b2 + 2b − 3a + 4. (∗) 841 − 1036 < 0, 0 < 841 + 58 − 777 + 4 2. Invoke Cauchy's Lemma: If a and b are odd positive integers satisfying (∗) then there exist nonnegative integers s, t, u, v such that a = s2 + t2 + u2 + v2 and b = s + t + u + v.
    [Show full text]
  • Winnovative HTML to PDF Converter for .NET
    TECHCALC - HELP CONTENTS 1. GENERAL Page 01 2. REVERSE POLISH NOTATION (RPN) Page 04 3. AUTOMATIC BACKUP Page 04 4. SCREEN TRANSITIONS Page 04 5. EDITING AN EXPRESSION Page 05 6. MEMORIES Page 05 7. HISTORY Page 06 8. TRIGONOMETRIC FUNCTIONS Page 06 9. POWER & ROOT FUNCTIONS Page 06 10. LOG & ANTILOG FUNCTIONS Page 07 11. PERMUTATIONS & COMBINATIONS Page 07 12. HCF, LCM, PRIME FACTORIZATION, REMAINDER, Δ% & CUMULATIVE % FUNCTIONS Page 07 13. STATISTICS FUNCTIONS Page 07 14. FACTORIAL FUNCTION Page 10 15. MODULUS FUNCTION Page 11 16. RANDOM NUMBERS Page 11 17. FRACTIONS MODE Page 11 18. HEX, OCT & BIN CALCULATIONS Page 11 19. LEFT HAND SHIFT & RIGHT HAND SHIFT Page 12 20. GRAPHING CALCULATIONS Page 12 21. CONVERSION FACTORS Page 13 22. CONSTANTS Page 13 23. MATRICES Page 14 24. COMPLEX NUMBERS Page 14 25. QUICK FORMULAS Page 15 26. CUSTOM FORMULAS Page 15 27. TIME CALCULATOR Page 15 28. EQUATION SOLVER Page 16 29. CALCULUS Page 17 30. PERIODIC TABLE Page 17 31. SIGMA AND PI NOTATION Page 17 32. PERCENTAGE CALCULATOR Page 17 33. MOLECULAR WEIGHT CALCULATOR Page 18 34. BALANCING CHEMICAL EQUATIONS Page 18 35. STATISTICS (GROUPED DATA) Page 18 36. NUMERICAL SEQUENCES Page 18 37. FEET AND INCHES CALCULATOR Page 19 38. FINANCIAL MODE Page 19 GENERAL Use the menu to change calculator modes (scroll to view all) - the action bar can be hidden via the 'Settings' if required. Some buttons have 2 values - short press gives main function, long press gives secondary function (in yellow). A wide variety of themes are available in the following categories: Standard Themes: Standard 1 is the default used by the application.
    [Show full text]
  • Figurate Numbers
    Figurate Numbers by George Jelliss June 2008 with additions November 2008 Visualisation of Numbers The visual representation of the number of elements in a set by an array of small counters or other standard tally marks is still seen in the symbols on dominoes or playing cards, and in Roman numerals. The word "calculus" originally meant a small pebble used to calculate. Bear with me while we begin with a few elementary observations. Any number, n greater than 1, can be represented by a linear arrangement of n counters. The cases of 1 or 0 counters can be regarded as trivial or degenerate linear arrangements. The counters that make up a number m can alternatively be grouped in pairs instead of ones, and we find there are two cases, m = 2.n or 2.n + 1 (where the dot denotes multiplication). Numbers of these two forms are of course known as even and odd respectively. An even number is the sum of two equal numbers, n+n = 2.n. An odd number is the sum of two successive numbers 2.n + 1 = n + (n+1). The even and odd numbers alternate. Figure 1. Representation of numbers by rows of counters, and of even and odd numbers by various, mainly symmetric, formations. The right-angled (L-shaped) formation of the odd numbers is known as a gnomon. These do not of course exhaust the possibilities. 1 2 3 4 5 6 7 8 9 n 2 4 6 8 10 12 14 2.n 1 3 5 7 9 11 13 15 2.n + 1 Triples, Quadruples and Other Forms Generalising the divison into even and odd numbers, the counters making up a number can of course also be grouped in threes or fours or indeed any nonzero number k.
    [Show full text]
  • TRIANGULAR REPUNIT—THERE IS but 1 a Repunit Is Any Integer That
    Czechoslovak Mathematical Journal, 60 (135) (2010), 1075–1077 TRIANGULAR REPUNIT—THERE IS BUT 1 John H. Jaroma, Ave Maria (Received June 27, 2009) Abstract. In this paper, we demonstrate that 1 is the only integer that is both triangular and a repunit. Keywords: repunit, triangular number MSC 2010 : 11A99 A repunit is any integer that can be written in decimal notation as a string of 1’s. Examples include 1, 11, 111, 1111, 11111,... Furthermore, if we denote rn to be the nth repunit then it follows that 10n − 1 (1) rn = . 9 Triangular numbers are those integers that can be represented by the number of dots evenly arranged in an equilateral triangle. More specifically, they are the numbers 1, 3, 6, 10, 15,... It follows that the nth triangular number, tn is the sum of the first n consecutive integers beginning with 1. In particular, for n > 1 n(n + 1) (2) tn = . 2 Now, the number 1 is both triangular and a repunit. It is the objective of this note to illustrate that 1 is the only such number. To this end, we state and prove the following lemma. It incorporates a result that [1] asserts had been known by the early Pythagoreans. Appearing in Platonic Questions, Plutarch states that eight times any triangular number plus one is a square. The result is actually necessary and sufficient. We demonstrate it as such here. 1075 Lemma. The integer n is triangular if and only if 8n +1 is a square. Proof. If n = tn, then by (2), n(n + 1) 8 +1=4n2 +4n +1=(2n + 1)2.
    [Show full text]
  • PELL FACTORIANGULAR NUMBERS Florian Luca, Japhet Odjoumani
    PUBLICATIONS DE L’INSTITUT MATHÉMATIQUE Nouvelle série, tome 105(119) (2019), 93–100 DOI: https://doi.org/10.2298/PIM1919093L PELL FACTORIANGULAR NUMBERS Florian Luca, Japhet Odjoumani, and Alain Togbé Abstract. We show that the only Pell numbers which are factoriangular are 2, 5 and 12. 1. Introduction Recall that the Pell numbers Pm m> are given by { } 1 αm βm P = − , for all m > 1, m α β − where α =1+ √2 and β =1 √2. The first few Pell numbers are − 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, 5741, 13860, 33461, 80782, 195025,... Castillo [3], dubbed a number of the form Ftn = n!+ n(n + 1)/2 for n > 1 a factoriangular number. The first few factoriangular numbers are 2, 5, 12, 34, 135, 741, 5068, 40356, 362925,... Luca and Gómez-Ruiz [8], proved that the only Fibonacci factoriangular numbers are 2, 5 and 34. This settled a conjecture of Castillo from [3]. In this paper, we prove the following related result. Theorem 1.1. The only Pell numbers which are factoriangular are 2, 5 and 12. Our method is similar to the one from [8]. Assuming Pm = Ftn for positive integers m and n, we use a linear forms in p-adic logarithms to find some bounds on m and n. The resulting bounds are large so we run a calculation to reduce the bounds. This computation is highly nontrivial and relates on reducing the diophantine equation Pm = Ftn modulo the primes from a carefully selected finite set of suitable primes. 2010 Mathematics Subject Classification: Primary 11D59, 11D09, 11D7; Secondary 11A55.
    [Show full text]
  • Patterns in Figurate Sequences
    Patterns in Figurate Sequences Concepts • Numerical patterns • Figurate numbers: triangular, square, pentagonal, hexagonal, heptagonal, octagonal, etc. • Closed form representation of a number sequence • Function notation and graphing • Discrete and continuous data Materials • Chips, two-color counters, or other manipulatives for modeling patterns • Student activity sheet “Patterns in Figurate Sequences” • TI-73 EXPLORER or TI-83 Plus/SE Introduction Mathematics has been described as the “science of patterns.” Patterns are everywhere and may appear as geometric patterns or numeric patterns or both. Figurate numbers are examples of patterns that are both geometric and numeric since they relate geometric shapes of polygons to numerical patterns. In this activity you will analyze, extend, and describe patterns involving figurate numbers and make connections between numeric and geometric representations of patterns. PTE: Algebra Page 1 © 2003 Teachers Teaching With Technology Patterns in Figurate Sequences Student Activity Sheet 1. Using chips or other manipulatives, analyze the following pattern and extend the pattern pictorially for two more terms. • • • • • • • • • • 2. Write the sequence of numbers that describes the quantity of dots above. 3. Describe this pattern in another way. 4. Extend and describe the following pattern with pictures, words, and numbers. • • • • • • • • • • • • • • 5. Analyze Table 1. Fill in each of the rows of the table. Table 1: Figurate Numbers Figurate 1st 2nd 3rd 4th 5th 6th 7th 8th nth Number Triangular 1 3 6 10 15 21 28 36 n(n+1)/2 Square 1 4 9 16 25 36 49 64 Pentagonal 1 5 12 22 35 51 70 Hexagonal 1 6 15 28 45 66 Heptagonal 1 7 18 34 55 Octagonal 1 8 21 40 Nonagonal 1 9 24 Decagonal 1 10 Undecagonal 1 ..
    [Show full text]
  • Polygonal Numbers 1
    Polygonal Numbers 1 Polygonal Numbers By Daniela Betancourt and Timothy Park Project for MA 341 Introduction to Number Theory Boston University Summer Term 2009 Instructor: Kalin Kostadinov 2 Daniela Betancourt and Timothy Park Introduction : Polygonal numbers are number representing dots that are arranged into a geometric figure. Starting from a common point and augmenting outwards, the number of dots utilized increases in successive polygons. As the size of the figure increases, the number of dots used to construct it grows in a common pattern. The most common types of polygonal numbers take the form of triangles and squares because of their basic geometry. Figure 1 illustrates examples of the first four polygonal numbers: the triangle, square, pentagon, and hexagon. Figure 1: http://www.trottermath.net/numthry/polynos.html As seen in the diagram, the geometric figures are formed by augmenting arrays of dots. The progression of the polygons is illustrated with its initial point and successive polygons grown outwards. The basis of polygonal numbers is to view all shapes and sizes of polygons as numerical values. History : The concept of polygonal numbers was first defined by the Greek mathematician Hypsicles in the year 170 BC (Heath 126). Diophantus credits Hypsicles as being the author of the polygonal numbers and is said to have came to the conclusion that the nth a-gon is calculated by 1 the formula /2*n*[2 + (n - 1)(a - 2)]. He used this formula to determine the number of elements in the nth term of a polygon with a sides. Polygonal Numbers 3 Before Hypsicles was acclaimed for defining polygonal numbers, there was evidence that previous Greek mathematicians used such figurate numbers to create their own theories.
    [Show full text]
  • Identifying Figurate Number Patterns
    Identifying Figurate Lesson 7-9 Number Patterns DATE TIME SRB 1 Draw the next three rectangular numbers. 58-61 2 a. Complete the list of the first 10 rectangular numbers. 2, 6, 12, 20, 30, 42 56,EM4_MJ2_G4_U07_L09_001A.ai 72, 90, 110 b. How did you get your answers? Sample answer: I kept multiplying the next 2 counting numbers. I knew 42 = 6 ⁎ 7, so to find the next rectangular number, I multiplied 7 ⁎ 8 = 56. 3 a. Continue the following pattern: 2 = 2 2 + 4 = 6 2 + 4 + 6 = 12 2 + 4 + 6 + 8 = 20 2 + 4 + 6 + 8 + 10 = 30 2 + 4 + 6 + 8 + 10 + 12 = 42 b. Describe the pattern. Sample answer: Each rectangular number is the sum of the even numbers in order, starting with 2. c. What pattern do you notice about the number of addends and the rectangular number? The number of addends is the same as the “number” of the rectangular number. For example, 30 is the fifth rectangular number, and it has 5 addends. d. Describe a similar pattern with square numbers. Sample answer: Each square number is the sum of the odd numbers in order, starting with 1. 1 = 1, 1 + 3 = 4, 1 + 3 + 5 = 9, 1 + 3 + 5 + 7 = 16, and so on. 252 4.OA.5, 4.NBT.6, SMP7, SMP8 Identifying Figurate Lesson 7-9 DATE TIME Number Patterns (continued) Try This 4 Triangular numbers are numbers that are the sum of consecutive counting numbers. For example, the triangular number 3 is the sum of 1 + 2, and the triangular number 6 is the sum of 1 + 2 + 3.
    [Show full text]