DOCSLIB.ORG

Towards Meaningful Software Metrics Aggregation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Towards Meaningful Software Metrics Aggregation Towards Meaningful Software Metrics Aggregation Maria Ulan, Welf L¨owe, Morgan Ericsson, Anna Wingkvist Department of Computer Science and Media Technology Linnaeus University, V¨axj¨o,Sweden fmaria.ulan j welf.lowe j morgan.ericsson j [email protected] The problem of metrics aggregation is addressed by the research community. Metrics are often defined at Abstract a method or class level, but quality assessment some- times requires insights at the system level. One bad Aggregation of software metrics is a challeng- metric value can be evened out by other good met- ing task, it is even more complex when it ric values when summing them up or computing their comes to considering weights to indicate the mean [1]. Some effort has been directed into met- relative importance of software metrics. These rics aggregation based on inequality indices [2,3], and weights are mostly determined manually, it based on thresholds [4{8] to map source code level mea- results in subjective quality models, which surements to software system rating. are hard to interpret. To address this chal- In this research, we do not consider aggregation lenge, we propose an automated aggregation along the structure of software artifacts, e.g., from approach based on the joint distribution of classes to the system. We focus on another type software metrics. To evaluate the effective- of metrics aggregation, from low-level to higher-level ness of our approach, we conduct an empir- quality properties, Mordal-Manet et al. call such type ical study on maintainability assessment for of aggregation metrics composition [9]. around 5 000 classes from open source soft- Different software quality models that use weighted ware systems written in Java and compare metrics aggregation have been proposed, such our approach with a classical weighted lin- as QMOOD [10], QUAMOCO [11], SIG [12], ear combination approach in the context of SQALE [13], and SQUALE [14]. The weights in these maintainability scoring and anomaly detec- models are defined based on experts' opinions or sur- tion. The results show that approaches assign veys. It is questionable whether manual weighting and similar scores, while our approach is more in- combination of the values with an arbitrary (not nec- terpretable, sensitive, and actionable. essarily linear) function are acceptable operations for metrics of different scales and distributions. Index terms| Software metrics, Aggregation, As a countermeasure, we propose to use a proba- Weights, Copula bilistic approach for metrics aggregation. In previous research, we considered software metrics to be equally 1 Introduction important and developed a software metrics visualiza- tion tool. This tool allowed the user to define and ma- Quality models provide a basic understanding of nipulate quality models to reason about where qual- what data to collect and what software metrics to ity problems were located, to detect patterns, correla- use. However, they do not provide how software tions, and anomalies [15]. (sub-)characteristics should be quantified, and metrics Here, we define metrics scores by probability as should be aggregated. complementary Cumulative Distribution Function and link them with joint probability by the so-called cop- Copyright © by the paper's authors. Use permitted under Cre- ula function. We determine weights from the joint dis- ative Commons License Attribution 4.0 International (CC BY 4.0). tribution and aggregate software metrics by weighted product of the scores. We formalize quality models In: D. Di Nucci, C. De Roover (eds.): Proceedings of the 18th Belgium-Netherlands Software Evolution Workshop, Brussels, to expresses quality as the probability of observing a Belgium, 28-11-2019, published at http://ceur-ws.org software artifact with equal or better quality. This 1 approach is objective since it relies solely on data. It 2. If all scores of one software artifact are greater or allows to modify quality models on the fly, and it cre- equal than all scores of another software artifact, ates a realistic scale since the distribution represents the same should be true for the overall scores. quality scores for a set of software artifacts. i l i l s1 ≥ s1 ^ · · · ^ sn ≥ sn ) i i l l 2 Approach Overview F (s1; : : : ; sn) ≥ F (s1; : : : ; sn); i l We consider a joint distribution of software metrics where sj = sj(ej(ai)); sj = sj(ej(al)) (4) values, and for each software artifact, we assign a probabilistic score. W.l.o.g, we assume that all soft- 3. If the software artifact perfectly meets all but one ware metrics are defined such that larger values indi- metric, the overall score is equal to that metrics cate lower quality. The joint distribution of software score. metrics provides the means of objective comparison F (1;:::; 1; sj; 1;:::; 1) = sj (5) of software artifacts in terms of their quality scores, We propose to express the degree of satisfaction which represent the relative rank of the software arti- with respect to a metric using probability. We define fact within the set of all software artifacts observed so the score function of Equation (1) as follows: far, i.e., how good or bad a quality score compare to other quality scores. Let A = fa1; : : : ; akg be a set of k software artifacts, sj(ej(a)) = P r(Ej > ej(a)) = CCDF ej (a) (6) and M = fm1; : : : ; mng be a set of n software metrics. Each software artifact is assessed by metrics from M, We calculate the Complementary Cumulative Dis- and the result of this assessment is represented as k×n tribution Function (CCDF). This score represents the performance matrix of metrics values. probability of finding another software artifact with an evaluation value greater than the given value. For a We denote by ej(ai) for 8i 2 f1; kg; 8j 2 f1; ng an (i; j)-entry, which shows the degree of performance multi-criteria case, we can specify a joint distribution in terms of n marginal distributions and a so-called for an software artifact ai measured for metric mj. We T k copula function [16]: denote by Ej = [ej(a1); : : : ; ej(ak)] 2 Ej the j-th col- umn of performance matrix, which represents metrics values for all software artifacts with respect to metric Cop(CCDF e1 (a);:::; CCDF en (a)) = mj where Ej is the domain of these values. P r(E1 > e1(a);:::;En > en(a)) (7) For each software artifact ai 2 A and metric mj 2 M, we define a score sj(ai), which indicates the degree The copula representation of a joint probability dis- to which this software artifact meets the requirements tribution allows us to model both marginal distribu- for the metric. Formally, for each metric mj we define tions and dependencies. The copula function Cop sat- a score function sj: isfies the signature (2) and fulfills the required proper- ties (3), (4), and (5). We consider a weight vector, where each wi repre- ej(a): A 7! Ej sents the relative importance of metric mi compared sj(e): Ej 7! [0; 1] (1) to the others: n Based on the score functions sj for each metric, our T X goal is to define an overall score function such that, for w = [w1; : : : ; wn] ; where wi = 1 (8) any software artifact, it indicates the degree to which i=1 this software artifact satisfies all metrics. Formally, we We compute weights using a non-linear exponen- are looking for a function: tial regression model for a sample of software artifacts mapping metrics scores of Equation(6) to copula value n F (s1; : : : ; sn) : [0; 1] 7! [0; 1] (2) of Equation(7). Note that these weights regard depen- Such an aggregation function takes an n-tuple of dencies between software metrics. Finally, we define metrics scores and returns a single overall score. We software metrics aggregation as a weighted composi- require the following properties: tion of metrics score functions: n 1. If a software artifact does not meet the require- Y wj F (s1; : : : ; sn) = sj (9) ments for one of the metrics, the overall score j=1 should be close to zero. We consider a software artifact al to be better than F (s1; : : : ; sn) ! 0 as sj ! 0 (3) or equally good as another software artifact ai, if the 2 total score according to Equation (2) of al is greater CBO, Coupling Between Objects than or equal the total score of ai: DIT, Depth of Inheritance Tree al ai , F (al) ≥ F (ai) (10) LCOM, Lack of Cohesion in Methods Aggregation is defined as a composition of the product, exponential, and CCDF functions, which are mono- NOC, Number Of Children tonic functions. Hence, the score which is obtained by aggregation allows to rank set A of software artifacts RFC, Response For a Class with respect to metrics set M: WMC, Weighted Method Count (using Cyclomatic Complexity as method weight) Rank(al) ≤ Rank(ai) , F (al) ≥ F (ai) (11) 3.2 Data Set Description From a practical point of view, probabilities can be We chose to investigate three open-source software calculated empirically, and each score can be obtained systems. The systems were chosen by such criteria: as a ratio of the number of software artifacts with lower (i) they are written in Java, (ii) available in GitHub, than a given metric value to the number jAj of software (iii) they were forked at least once, (iv) they are suf- artifacts. ficiently large (several tens of thousands of lines of The proposed aggregation approach makes it possi- code and several hundreds of classes), and (v) they ble to express the score for a software artifact as the have been under active development for several years. probability to observe something with equal or worse The projects we selected are three well-known and metrics values, based on all software artifacts observed.
Load more

Recommended publications
  • Working with Unreliable Observers Using Reactive Extensions
    Master thesis WORKING WITH UNRELIABLE OBSERVERS USING REACTIVE EXTENSIONS November 10, 2016 Dorus Peelen (s4167821) Computing science Radboud University [email protected] — Supervisors: Radboud University: Rinus Plasmeijer Aia Software: Jeroen ter Hofstede Contents 1 Introduction 5 1.1 Overview of thesis . .7 2 Background 8 2.1 Aia Software . .8 2.2 Current situation . .8 2.3 The use case . .9 2.3.1 Technical details . 10 2.3.2 Potential problems . 11 2.4 Problem description . 11 2.5 Desired Properties of the new system . 11 3 Overview of Rx 13 3.1 Basic Ideas of Rx . 13 3.2 Observer and Observable . 15 3.3 Hot vs Cold observables . 15 3.4 Marble diagrams . 16 3.5 Transformations on Event Streams . 16 3.6 Schedulers . 16 3.7 Control process in Rx . 17 3.8 Interactive vs reactive . 18 3.9 Push-back and backpressure . 18 3.10 Operators with unbounded Queue . 19 3.11 Explanation and example of different operators in Rx . 19 3.11.1 Select .................................. 19 3.11.2 SelectMany ............................... 20 3.11.3 Where .................................. 20 3.11.4 Delay .................................. 20 3.11.5 Merge and Concat ........................... 21 3.11.6 Buffer and Window ........................... 21 3.11.7 GroupBy ................................. 21 3.11.8 Amb .................................... 21 3.11.9 Debounce, Sample and Throttle ................... 22 3.11.10 ObserveOn ................................ 22 3.12 Related work . 22 3.12.1 TPL . 23 3.12.2 iTasks . 23 4 The experiment 25 4.1 Important properties . 25 4.2 Test architecture . 26 4.2.1 Design . 26 2 4.2.2 Concepts .
    [Show full text]
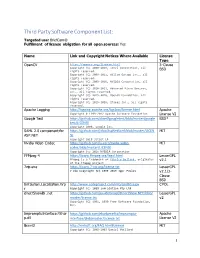
  • Third Party Software Component List: Targeted Use: Briefcam® Fulfillment of License Obligation for All Open Sources: Yes
    Third Party Software Component List: Targeted use: BriefCam® Fulfillment of license obligation for all open sources: Yes Name Link and Copyright Notices Where Available License Type OpenCV https://opencv.org/license.html 3-Clause Copyright (C) 2000-2019, Intel Corporation, all BSD rights reserved. Copyright (C) 2009-2011, Willow Garage Inc., all rights reserved. Copyright (C) 2009-2016, NVIDIA Corporation, all rights reserved. Copyright (C) 2010-2013, Advanced Micro Devices, Inc., all rights reserved. Copyright (C) 2015-2016, OpenCV Foundation, all rights reserved. Copyright (C) 2015-2016, Itseez Inc., all rights reserved. Apache Logging http://logging.apache.org/log4cxx/license.html Apache Copyright © 1999-2012 Apache Software Foundation License V2 Google Test https://github.com/abseil/googletest/blob/master/google BSD* test/LICENSE Copyright 2008, Google Inc. SAML 2.0 component for https://github.com/jitbit/AspNetSaml/blob/master/LICEN MIT ASP.NET SE Copyright 2018 Jitbit LP Nvidia Video Codec https://github.com/lu-zero/nvidia-video- MIT codec/blob/master/LICENSE Copyright (c) 2016 NVIDIA Corporation FFMpeg 4 https://www.ffmpeg.org/legal.html LesserGPL FFmpeg is a trademark of Fabrice Bellard, originator v2.1 of the FFmpeg project 7zip.exe https://www.7-zip.org/license.txt LesserGPL 7-Zip Copyright (C) 1999-2019 Igor Pavlov v2.1/3- Clause BSD Infralution.Localization.Wp http://www.codeproject.com/info/cpol10.aspx CPOL f Copyright (C) 2018 Infralution Pty Ltd directShowlib .net https://github.com/pauldotknopf/DirectShow.NET/blob/ LesserGPL
    [Show full text]
  • An Opinionated Guide to Technology Frontiers
    TECHNOLOGY RADAR An opinionated guide to technology frontiers Volume 24 #TWTechRadar thoughtworks.com/radar The Technology Advisory Board (TAB) is a group of 20 senior technologists at Thoughtworks. The TAB meets twice a year face-to-face and biweekly by phone. Its primary role is to be an advisory group for Thoughtworks CTO, Contributors Rebecca Parsons. The Technology Radar is prepared by the The TAB acts as a broad body that can look at topics that affect technology and technologists at Thoughtworks. With the ongoing global pandemic, we Thoughtworks Technology Advisory Board once again created this volume of the Technology Radar via a virtual event. Rebecca Martin Fowler Bharani Birgitta Brandon Camilla Cassie Parsons (CTO) (Chief Scientist) Subramaniam Böckeler Byars Crispim Shum Erik Evan Fausto Hao Ian James Lakshminarasimhan Dörnenburg Bottcher de la Torre Xu Cartwright Lewis Sudarshan Mike Neal Perla Rachel Scott Shangqi Zhamak Mason Ford Villarreal Laycock Shaw Liu Dehghani TECHNOLOGY RADAR | 2 © Thoughtworks, Inc. All Rights Reserved. About the Radar Thoughtworkers are passionate about technology. We build it, research it, test it, open source it, write about it and constantly aim to improve it — for everyone. Our mission is to champion software excellence and revolutionize IT. We create and share the Thoughtworks Technology Radar in support of that mission. The Thoughtworks Technology Advisory Board, a group of senior technology leaders at Thoughtworks, creates the Radar. They meet regularly to discuss the global technology strategy for Thoughtworks and the technology trends that significantly impact our industry. The Radar captures the output of the Technology Advisory Board’s discussions in a format that provides value to a wide range of stakeholders, from developers to CTOs.
    [Show full text]
  • Front-End Development with ASP.NET Core, Angular, And
    Table of Contents COVER TITLE PAGE FOREWORD INTRODUCTION WHY WEB DEVELOPMENT REQUIRES POLYGLOT DEVELOPERS WHO THIS BOOK IS FOR WHAT THIS BOOK COVERS HOW THIS BOOK IS STRUCTURED WHAT YOU NEED TO USE THIS BOOK CONVENTIONS SOURCE CODE ERRATA 1 What’s New in ASP.NET Core MVC GETTING THE NAMES RIGHT A BRIEF HISTORY OF THE MICROSOFT .NET WEB STACK .NET CORE INTRODUCING ASP.NET CORE NEW FUNDAMENTAL FEATURES OF ASP.NET CORE AN OVERVIEW OF SOME ASP.NET CORE MIDDLEWARE ASP.NET CORE MVC SUMMARY 2 The Front‐End Developer Toolset ADDITIONAL LANGUAGES YOU HAVE TO KNOW JAVASCRIPT FRAMEWORKS CSS FRAMEWORKS PACKAGE MANAGERS TASK RUNNERS SUMMARY 3 Angular in a Nutshell ANGULAR CONCEPTS THE LANGUAGE OF ANGULAR SETTING UP AN ANGULAR PROJECT THE STRUCTURE OF AN ANGULAR APP DATA BINDING DIRECTIVES SERVICES AND DEPENDECY INJECTION MULTIPLE COMPONENTS INPUT AND OUTPUT PROPERTIES TALKING TO THE BACK END USING ANGULAR WITH ASP.NET MVC VISUAL STUDIO 2017 SUPPORT FOR ANGULAR SUMMARY 4 Bootstrap in a Nutshell INTRODUCTION TO BOOTSTRAP BOOTSTRAP STYLES COMPONENTS JAVASCRIPT CUSTOMIZING BOOTSTRAP WITH LESS BOOTSTRAP SUPPORT IN VISUAL STUDIO 2017 AND ASP.NET CORE SUMMARY 5 Managing Dependencies with NuGet and Bower GENERAL CONCEPTS NUGET NPM (NODE.JS PACKAGE MANAGER) BOWER SUMMARY 6 Building Your Application with Gulp and webpack WHAT FRONT‐END BUILD SYSTEMS ARE FOR A DEEPER LOOK AT GULP INTRODUCTION TO WEBPACK VISUAL STUDIO 2017 AND BUILD SYSTEMS SUMMARY 7 Deploying ASP.NET Core THE NEW HOSTING MODEL OF ASP.NET CORE INSTALLING ON INTERNET INFORMATION SERVICES ON PREMISE
    [Show full text]
  • Rxada: an Ada Implementation of the Reactivex API - 1 PREVIOUSLY, in ADA-EUROPE 2007
    RxAda: An Ada implementation of the ReactiveX API Alejandro R. Mosteo 2017-jun-13 2017-jun-13 - RxAda: An Ada implementation of the ReactiveX API - 1 PREVIOUSLY, IN ADA-EUROPE 2007... SANCTA: An Ada 2005 General-Purpose Architecture for Mobile Robotics Research 2017-jun-13 - RxAda: An Ada implementation of the ReactiveX API - 2 ABOUT ME Robotics, Perception, and Real-Time group (RoPeRT) http://robots.unizar.es/ Universidad de Zaragoza, Spain 2017-jun-13 - RxAda: An Ada implementation of the ReactiveX API - 3 CONTENTS • Motivation • What is ReactiveX – Language agnostic – Java – Ada • RxAda – Design challenges/decisions – Current implementation status – Future steps 2017-jun-13 - RxAda: An Ada implementation of the ReactiveX API - 4 PERSONAL MOTIVATION • Android development – Questionable design decisions for background tasks that interact with the GUI • Found RxJava – Simpler, saner way of doing multitasking – Documented comprehensively – Very active community in the Rx world • Achievable in Ada? – Aiming for the RxJava simplicity of use 2017-jun-13 - RxAda: An Ada implementation of the ReactiveX API - 5 EVENT-DRIVEN / ASYNCHRONOUS SYSTEMS <User drags map> ↓ Find nearby items ↓⌛ Request images ↓⌛↓⌛↓⌛↓⌛ Crop/Process image ↓⌛ Update GUI markers 2017-jun-13 - RxAda: An Ada implementation of the ReactiveX API - 6 OVERVIEW Event-driven systems ↓ Reactive Programming (philosophy) ↓ ReactiveX / Rx (specification) ↓ Rx.Net, RxJava, RxJS, RxC++, … ↓ RxAda 2017-jun-13 - RxAda: An Ada implementation of the ReactiveX API - 7 REACTIVE MANIFESTO (2014-sep-16
    [Show full text]
  • Coverity Static Analysis
    Coverity Static Analysis Quickly find and fix Overview critical security and Coverity® gives you the speed, ease of use, accuracy, industry standards compliance, and quality issues as you scalability that you need to develop high-quality, secure applications. Coverity identifies code critical software quality defects and security vulnerabilities in code as it’s written, early in the development process when it’s least costly and easiest to fix. Precise actionable remediation advice and context-specific eLearning help your developers understand how to fix their prioritized issues quickly, without having to become security experts. Coverity Benefits seamlessly integrates automated security testing into your CI/CD pipelines and supports your existing development tools and workflows. Choose where and how to do your • Get improved visibility into development: on-premises or in the cloud with the Polaris Software Integrity Platform™ security risk. Cross-product (SaaS), a highly scalable, cloud-based application security platform. Coverity supports 22 reporting provides a holistic, more languages and over 70 frameworks and templates. complete view of a project’s risk using best-in-class AppSec tools. Coverity includes Rapid Scan, a fast, lightweight static analysis engine optimized • Deployment flexibility. You for cloud-native applications and Infrastructure-as-Code (IaC). Rapid Scan runs decide which set of projects to do automatically, without additional configuration, with every Coverity scan and can also AppSec testing for: on-premises be run as part of full CI builds with conventional scan completion times. Rapid Scan can or in the cloud. also be deployed as a standalone scan engine in Code Sight™ or via the command line • Shift security testing left.
    [Show full text]
  • Santiago Quintero Pabón –
    LIX - École Polytechnique Palaiseau Santiago Quintero France Æ +33 (0) 7 67 39 73 30 Pabón Q [email protected] Contact Information Last Name: Quintero Pabón Given Name: Santiago Birth Date: 21-oct-1994 Nationality: Colombian Education Pontificia Universidad Javeriana Cali, CO + Five years B.Sc. Degree in Computer Science and Engineering, (equivalent to a master degree) 2012-2017 École Polytechnique Palaiseau, FR + PhD in Computer Sciences, Thesis: "Foundational approach to computation in today’s systems" 2018-Current Supervisors: Catuscia Palamidessi, Frank Valencia. Work Experience COMETE at LIX, École Polytechnique Palaiseau, FR + PhD Student 2018-Current AVISPA research group at Pontificia Universidad Javeriana Cali, CO + Research Assistant 2018 PORTAL ACTUALICESE.COM S.A.S. Cali, CO + Development Analyst 2017-2018 COMETE research group at Inria-Saclay Palaiseau, FR + Research Intern November 2017 Pontificia Universidad Javeriana Cali, CO + Teaching Assistant 2014-2016 Teaching Assistant....................................................................................................... Courses: Introduction to Programming, Programming Fundamentals and Structures, Logic in Computer Science, Computability and Formal Languages, Introduction to Systems Modeling. Major Projects............................................................................................................. + October 2015 - June 2016: ’Financial inclusion for the emerging middle class in Colombia’ Designed, prototyped and developed a financial
    [Show full text]
  • Rxpy Documentation Release 3.1.1
    RxPY Documentation Release 3.1.1 Dag Brattli Jul 16, 2020 CONTENTS 1 Installation 3 2 Rationale 5 3 Get Started 7 3.1 Operators and Chaining.........................................8 3.2 Custom operator.............................................9 3.3 Concurrency............................................... 10 4 Migration 15 4.1 Pipe Based Operator Chaining...................................... 15 4.2 Removal Of The Result Mapper..................................... 16 4.3 Scheduler Parameter In Create Operator................................. 16 4.4 Removal Of List Of Observables.................................... 17 4.5 Blocking Observable........................................... 17 4.6 Back-Pressure.............................................. 18 4.7 Time Is In Seconds............................................ 18 4.8 Packages Renamed............................................ 18 5 Operators 19 5.1 Creating Observables........................................... 19 5.2 Transforming Observables........................................ 19 5.3 Filtering Observables........................................... 20 5.4 Combining Observables......................................... 20 5.5 Error Handling.............................................. 20 5.6 Utility Operators............................................. 21 5.7 Conditional and Boolean Operators................................... 21 5.8 Mathematical and Aggregate Operators................................. 21 5.9 Connectable Observable Operators..................................
    [Show full text]
  • ASP.NET Core 2 and Angular 5
    www.EBooksWorld.ir ASP.NET Core 2 and Angular 5 Full-stack web development with .NET Core and Angular Valerio De Sanctis BIRMINGHAM - MUMBAI ASP.NET Core 2 and Angular 5 Copyright © 2017 Packt Publishing All rights reserved. No part of this book may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, without the prior written permission of the publisher, except in the case of brief quotations embedded in critical articles or reviews. Every effort has been made in the preparation of this book to ensure the accuracy of the information presented. However, the information contained in this book is sold without warranty, either express or implied. Neither the author, nor Packt Publishing, and its dealers and distributors will be held liable for any damages caused or alleged to be caused directly or indirectly by this book. Packt Publishing has endeavored to provide trademark information about all of the companies and products mentioned in this book by the appropriate use of capitals. However, Packt Publishing cannot guarantee the accuracy of this information. First published: November 2017 Production reference: 1221117 Published by Packt Publishing Ltd. Livery Place 35 Livery Street Birmingham B3 2PB, UK. ISBN 978-1-78829-360-0 www.packtpub.com Credits Author Copy Editor Valerio De Sanctis Shaila Kusanale Reviewers Project Coordinator Ramchandra Vellanki Devanshi Doshi Juergen Gutsch Commissioning Editor Proofreader Ashwin Nair Safis Editing Acquisition Editor Indexer Reshma Raman Rekha Nair Content Development Editor Graphics Onkar Wani Jason Monteiro Technical Editor Production Coordinator Akhil Nair Aparna Bhagat About the Author Valerio De Sanctis is a skilled IT professional with over 12 years of experience in lead programming, web-based development, and project management using ASP.NET, PHP, and Java.
    [Show full text]
  • Learning Objectives in This Part of the Module
    Applying Key Methods in the Single Class (Part 3) Douglas C. Schmidt [email protected] www.dre.vanderbilt.edu/~schmidt Professor of Computer Science Institute for Software Integrated Systems Vanderbilt University Nashville, Tennessee, USA Learning Objectives in this Part of the Lesson • Recognize key methods in the Random random = new Random(); Single class & how they are applied in the case studies Single<BigFraction> m1 = makeBigFraction(random); • Case study ex1 Single<BigFraction> m2 = • Case study ex2 makeBigFraction(random); • Case study ex3 return m1 .zipWith(m2, return Single BigFraction::add) .just(BigFractionUtils .makeBigFraction(...) .doOnSuccess .multiply(sBigReducedFrac)) (mixedFractionPrinter) .subscribeOn .then(); (Schedulers.parallel()); See github.com/douglascraigschmidt/LiveLessons/tree/master/Reactive/Single/ex32 Applying Key Methods in the Single Class in ex3 3 Applying Key Methods in the Single Class in ex3 • ex3 shows how to apply RxJava Random random = new Random(); features asynchronously to perform various Single operations Single<BigFraction> m1 = makeBigFraction(random); • e.g., subscribeOn(), doOnSuccess(), Single<BigFraction> m2 = ignoreElement(), just(), zipWith(), & makeBigFraction(random); Schedulers.computation() return m1 return Single .zipWith(m2, .just(BigFractionUtils BigFraction::add) .makeBigFraction(...) .multiply(sReducedFrac)) .doOnSuccess .doOnSuccess(fractionPrinter) (mixedFractionPrinter) .subscribeOn (Schedulers.computation()); .ignoreElement(); See github.com/douglascraigschmidt/LiveLessons/tree/master/Reactive/Single/ex34
    [Show full text]
  • Interactive Development Environment for Probabilistic Programming
    Maria I. Gorinova Interactive Development Environment for Probabilistic Programming Computer Science Tripos, Part II Clare College May 14, 2015 Proforma Name and College: Maria I. Gorinova, Clare College Project Title: Interactive Development Environment for Probabilistic Programming Examination: Computer Science Tripos Part II, 2015 Word Count: 119021 Project Originator: Alan Blackwell and Advait Sarkar Supervisor: Advait Sarkar Original Aims of the Project To implement an interactive development environment, which allows the pro- grammer to use the probabilistic programming framework Infer.NET. The en- vironment must support visualisations of the graphical models described by the source code, as well as of the probability density functions of random variables that have been declared. In addition, the environment must be live, meaning it provides run-time feedback about the execution of the source code. Update must be edit-triggered, meaning that re-compilation occurs when the code is changed, without the compiler having to be explicitly invoked by the user. Work Completed The work outlined in the original project proposal was successfully implemented, resulting in an IDE which meets all success criteria. In addition, several small features such as text highlighting and code navigation were added to the user interface. A user study was conducted to evaluate the usability of the software. The environment proves to significantly improve users' experience by reducing the probabilistic programming tasks completion time and the level of confusion
    [Show full text]
  • Reactive Stream Processing for Data-Centric Publish/Subscribe
    Reactive Stream Processing for Data-centric Publish/Subscribe Shweta Khare, Kyoungho An, Aniruddha Gokhale Sumant Tambe, Ashish Meena Dept of EECS, Vanderbilt University Real-Time Innovations Nashville, TN 37212, USA Sunnyvale, CA 94089, USA {shweta.p.khare,kyoungho.an,a.gokhale}@vanderbilt.edu {sumant,ashish}@rti.com ABSTRACT 1. INTRODUCTION The Internet of Things (IoT) paradigm has given rise to The Internet of Things (IoT) is a significant expansion of a new class of applications wherein complex data analytics the Internet to include physical devices; thereby bridging the must be performed in real-time on large volumes of fast- divide between the physical world and cyberspace. These moving and heterogeneous sensor-generated data. Such data devices or \things" are uniquely identifiable, fitted with sen- streams are often unbounded and must be processed in a sors and actuators, which enable them to gather informa- distributed and parallel manner to ensure timely process- tion about their environment and respond intelligently [8]. ing and delivery to interested subscribers. Dataflow archi- The Industrial IoT (IIoT){distinct from consumer IoT{will tectures based on event-based design have served well in help realize critical infrastructures, such as smart-grids, in- such applications because events support asynchrony, loose telligent transportation systems, advanced manufacturing, coupling, and helps build resilient, responsive and scalable health-care tele-monitoring, etc. Industrial IoT are also applications. However, a unified programming model for called Cyber-Physical Systems (CPSs). They share sev- event processing and distribution that can naturally com- eral key cross-cutting aspects. First, they are often large- pose the processing stages in a dataflow while exploiting the scale, distributed systems comprising several, potentially inherent parallelism available in the environment and com- mobile, publishers of information that produce large volumes putation is still lacking.
    [Show full text]