DOCSLIB.ORG

Linear Moments: an Overview

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Linear Moments: an Overview International Journal of Business and Statistical Analysis ISSN (2384-4663) Int. J. Bus. Stat. Ana. 2, No. 2 (July-2015) Linear Moments: An Overview A.F. Kandeel1 1 Department of Statistics and Mathematics, Faculty of Commerece, Benha University, Benha, Egypt Received 5 February 2015, Revised 1 April,. 2015, Accepted 5 April 2015, Published 1st July 2015 Abstract: Many statistical techniques are based on the use of linear combinations of order statistics that called linear moments. L-moments are a sequence of statistics used to summarize the shape of a probability distribution. They are linear combinations of order statistics analogous to conventional moments, and can be used to calculate quantities analogous to standard deviation, skewness and kurtosis, termed the L-scale, L-skewness and L-kurtosis respectively. In this paper an overview for recent works in L- moments is presented. Keywords: Order statistics, L-moments, TL-moments, LQ-moments, Quantile function. to the standard errors of L-moments to be finite, only the 1. INTRODUCTION distribution is required to have finite variance and no Many statistical techniques are based on the use of higher-order moments need be finite. Also, though linear combinations of order statistics (or quantile moment ratios can be arbitrarily large, sample moment function), but there has not been developed a unified ratios have algebraic bounds but sample L-moment ratios theory of estimation covering the characterization of can take any values that the corresponding population probability distribution, until Hosking (1990) introduced quantities can. L-moments, as an alternative to the classical moments. In addition, L-moments have properties that hold in a So, L-moments are summary statistics for probability wide range of practical situations. L-moments also give distributions and data samples. They provide measures of asymptotic approximations to sampling distributions location, dispersion, skewness, kurtosis, and other aspects better than classical moments and provide better of the shape of probability distributions or data samples. identification of the parent distribution which generated a However, The L in L-moments emphasizes the particular data sample (see Hosking (1990)). construction of L-moments from linear combinations of Furthermore, L-moments are less sensitive to outlying order statistics. data values and yield, sometimes, more efficient Sillitto (1969) has derived an approximation to the parameter estimates than the maximum likelihood inverse distribution function (the quantile function) in estimates (Vogel and Fennessey (1993)). terms of population L-moments without referring to L- But, the main shortage in L-moments is that they do moments. Also, he gave the sample version of the not exist for the distribution which has infinite mean and quantile function in terms of sample L-moments without less efficient for heavy tail distributions. studying its properties. A formal and comprehensive Mudholkar and Hutson (1998), introduced, as a treatment of L-moments was developed by Hosking result of the previous shortage, the LQ-moments, as a (1990), who established foundational results supporting a robust version of L-moments in which expectation of the new methodology in data analysis and inference based on conceptual order statistics (in the definition of population L-moments. L-moments) is replaced by a class of robust location Hosking (1990) concluded that the L-moments, as a measures defined in terms of simple linear combinations function of the quantile function, have various theoretical of symmetric quantiles of the distributions of the order advantages over the classical moments. For example, for statistics, such as median and trimean. L-moments of a probability distribution to be meaningful, Elamir and Seheult (2003) introduced Trimmed L- we require only that the distribution has a finite mean; no moments (TL-moments) as an alternative to LQ-moments higher-order moments need be finite. Similarly, in order and natural generalization of L-moments that do not E-mail address: [email protected] http://journals.uob.edu.bh 86 A.F. Kandeel: Linear Moments: An Overview require the mean of underlying distribution to exist. TL- characterizing life distributions and other applications. moments depend on giving zero weight to extreme The role of certain quantile functions and quantile-based observations. Therefore, they are defined for heavy tailed concepts in reliability analysis are also investigated. distributions where they do not involve some values at Several studies had been done using and applying the the extreme ends of the distribution. method of TL-moments as natural generalization of L- As interested in statistical modeling using heavy- moments: tailed distributions is increasing, so is the important of(a) Some of these studies concerned to introduce the potential by the L-moment and TL-moment theoretical results for TL-moments method are as approaches. The need of linear moments has been follows: developed in support of regional frequency analysis in Karvanen (2006) proposed parametric families from environmental science, which treats the quantile of quantile functions of distributions. This class of distributions of variables such as annual maximum parametric families is called quantile mixtures, which precipitation, stream flow, wind speed observed at each contain a wide range of different distributions that have site in a given network. Hosking and Wallis (1997) practical importance. He introduced two parametric provide an excellent exposition. Also linear moments families: the normal-polynomial quantile mixture and the approach has special utility in applications where Cauchy-polynomial quantile mixture. And he used the descriptive estimates (location, spread, skewness, and methods of L-moments and TL-moments to estimate the kurtosis) more stable than the usual central moments are parameters of the two quantile mixtures respectively. The critically needed. Such concern arise, for example, in proposed quantile mixtures are applied to model monthly, volatility estimation in financial risk management weekly and daily returns of some major stock indexes. involving market variables such as stock indices, interest Abdul-Moniem (2007) applied the method of L- rates; see, Serfling (1980) , Embrechts et al. (1997), moment and TL-moment estimators to estimate the Leonowicz et al. (2005) and Willinger et al. (1998). parameters of exponential distribution. TL-moments have various theoretical advantages. Asquith (2007) derived analytical solutions for the For example, TL-moments give more robust estimators first five L-moments and TL-moments (in case of than L-moments in the presence of outliers. Moreover, symmetrical trimming (1,1) in terms of a four-parameters population TL-moments may be well defined where the generalized Lambda distribution (GLD) in asymmetric corresponding population L-moments (or central case. And, because that asymmetric GLD needs moments ) do not exist , for example, the first population numerical methods to compute the parameters from the TL-moment is well defined for a Cauchy distribution, but L-moments or TL-moments, algorithms are suggested for the first population L-moment, the population mean, does parameter estimation. Application of the GLD using both not exist (see, Elamir and Seheult (2003)). L-moments and TL-moment parameter estimates from Also, their sample variance and covariance can be example data is demonstrated, a small simulation study obtained in closed form (see, Elamir and Seheult (2003)). of the 98th percentile (far-right tail) is conducted for a In addition, TL-moments ratios are bounded for any heavy-tail GLD with high-outlier contamination. The trimmed value (see, Hosking (2007 and Elamir et al simulations showed, with respect to estimation of the (2010)). 98th-percent quantile, that TL-moments are less biased Hosking (2007) has derived of approximation to the (more robust) in the presence of high-outlier quantile function in terms of population TL-moments. contamination. Elamir (2009) introduced properties of this approximate Hosking (2007) derived some further theoretical function by minimizing the weighted mean square error results for TL-moments. He defined the TL-moments in between the population quantile function and its TL- terms of shifted jacobi polynomials, and he introduced a moments representation. Also, he studied properties of representation for the quantile function as a weighted the corresponding sample estimator. He concluded that function of orthogonal polynomials in which the the estimators have a good approximation to population coefficients are related to TL-moments. quantile for a broad class of probability distribution Abdul-Moniem and Selim (2009) derived the TL- functions. moments and L-moments of the generalized Pareto Also, Elamir (2010) derived an optimal choice for distribution (GPD), and they used it to obtain the first the amount of trimming from known distributions, based four TL-moments and L-moments. They introduced the on the minimum sum of the absolute value of the errors TL-skewness, L-skewness, TL-kurtosis and L-kurtosis between the quantile probability function and its TL- for the GPD. They used the TL-moments and L-moments moments representation. Nair and Vineshkumar (2010) to estimate the parameters for the GPD. Also, they study the properties of L-moments of residual life in the introduced a numerical illustrate for the new results. context of modeling lifetime data. They introduced
Load more

Recommended publications
  • Concentration and Consistency Results for Canonical and Curved Exponential-Family Models of Random Graphs
    CONCENTRATION AND CONSISTENCY RESULTS FOR CANONICAL AND CURVED EXPONENTIAL-FAMILY MODELS OF RANDOM GRAPHS BY MICHAEL SCHWEINBERGER AND JONATHAN STEWART Rice University Statistical inference for exponential-family models of random graphs with dependent edges is challenging. We stress the importance of additional structure and show that additional structure facilitates statistical inference. A simple example of a random graph with additional structure is a random graph with neighborhoods and local dependence within neighborhoods. We develop the first concentration and consistency results for maximum likeli- hood and M-estimators of a wide range of canonical and curved exponential- family models of random graphs with local dependence. All results are non- asymptotic and applicable to random graphs with finite populations of nodes, although asymptotic consistency results can be obtained as well. In addition, we show that additional structure can facilitate subgraph-to-graph estimation, and present concentration results for subgraph-to-graph estimators. As an ap- plication, we consider popular curved exponential-family models of random graphs, with local dependence induced by transitivity and parameter vectors whose dimensions depend on the number of nodes. 1. Introduction. Models of network data have witnessed a surge of interest in statistics and related areas [e.g., 31]. Such data arise in the study of, e.g., social networks, epidemics, insurgencies, and terrorist networks. Since the work of Holland and Leinhardt in the 1970s [e.g., 21], it is known that network data exhibit a wide range of dependencies induced by transitivity and other interesting network phenomena [e.g., 39]. Transitivity is a form of triadic closure in the sense that, when a node k is connected to two distinct nodes i and j, then i and j are likely to be connected as well, which suggests that edges are dependent [e.g., 39].
    [Show full text]
  • Use of Statistical Tables
    TUTORIAL | SCOPE USE OF STATISTICAL TABLES Lucy Radford, Jenny V Freeman and Stephen J Walters introduce three important statistical distributions: the standard Normal, t and Chi-squared distributions PREVIOUS TUTORIALS HAVE LOOKED at hypothesis testing1 and basic statistical tests.2–4 As part of the process of statistical hypothesis testing, a test statistic is calculated and compared to a hypothesised critical value and this is used to obtain a P- value. This P-value is then used to decide whether the study results are statistically significant or not. It will explain how statistical tables are used to link test statistics to P-values. This tutorial introduces tables for three important statistical distributions (the TABLE 1. Extract from two-tailed standard Normal, t and Chi-squared standard Normal table. Values distributions) and explains how to use tabulated are P-values corresponding them with the help of some simple to particular cut-offs and are for z examples. values calculated to two decimal places. STANDARD NORMAL DISTRIBUTION TABLE 1 The Normal distribution is widely used in statistics and has been discussed in z 0.00 0.01 0.02 0.03 0.050.04 0.05 0.06 0.07 0.08 0.09 detail previously.5 As the mean of a Normally distributed variable can take 0.00 1.0000 0.9920 0.9840 0.9761 0.9681 0.9601 0.9522 0.9442 0.9362 0.9283 any value (−∞ to ∞) and the standard 0.10 0.9203 0.9124 0.9045 0.8966 0.8887 0.8808 0.8729 0.8650 0.8572 0.8493 deviation any positive value (0 to ∞), 0.20 0.8415 0.8337 0.8259 0.8181 0.8103 0.8206 0.7949 0.7872 0.7795 0.7718 there are an infinite number of possible 0.30 0.7642 0.7566 0.7490 0.7414 0.7339 0.7263 0.7188 0.7114 0.7039 0.6965 Normal distributions.
    [Show full text]
  • 18.440: Lecture 9 Expectations of Discrete Random Variables
    18.440: Lecture 9 Expectations of discrete random variables Scott Sheffield MIT 18.440 Lecture 9 1 Outline Defining expectation Functions of random variables Motivation 18.440 Lecture 9 2 Outline Defining expectation Functions of random variables Motivation 18.440 Lecture 9 3 Expectation of a discrete random variable I Recall: a random variable X is a function from the state space to the real numbers. I Can interpret X as a quantity whose value depends on the outcome of an experiment. I Say X is a discrete random variable if (with probability one) it takes one of a countable set of values. I For each a in this countable set, write p(a) := PfX = ag. Call p the probability mass function. I The expectation of X , written E [X ], is defined by X E [X ] = xp(x): x:p(x)>0 I Represents weighted average of possible values X can take, each value being weighted by its probability. 18.440 Lecture 9 4 Simple examples I Suppose that a random variable X satisfies PfX = 1g = :5, PfX = 2g = :25 and PfX = 3g = :25. I What is E [X ]? I Answer: :5 × 1 + :25 × 2 + :25 × 3 = 1:75. I Suppose PfX = 1g = p and PfX = 0g = 1 − p. Then what is E [X ]? I Answer: p. I Roll a standard six-sided die. What is the expectation of number that comes up? 1 1 1 1 1 1 21 I Answer: 6 1 + 6 2 + 6 3 + 6 4 + 6 5 + 6 6 = 6 = 3:5. 18.440 Lecture 9 5 Expectation when state space is countable II If the state space S is countable, we can give SUM OVER STATE SPACE definition of expectation: X E [X ] = PfsgX (s): s2S II Compare this to the SUM OVER POSSIBLE X VALUES definition we gave earlier: X E [X ] = xp(x): x:p(x)>0 II Example: toss two coins.
    [Show full text]
  • 5. the Student T Distribution
    Virtual Laboratories > 4. Special Distributions > 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 5. The Student t Distribution In this section we will study a distribution that has special importance in statistics. In particular, this distribution will arise in the study of a standardized version of the sample mean when the underlying distribution is normal. The Probability Density Function Suppose that Z has the standard normal distribution, V has the chi-squared distribution with n degrees of freedom, and that Z and V are independent. Let Z T= √V/n In the following exercise, you will show that T has probability density function given by −(n +1) /2 Γ((n + 1) / 2) t2 f(t)= 1 + , t∈ℝ ( n ) √n π Γ(n / 2) 1. Show that T has the given probability density function by using the following steps. n a. Show first that the conditional distribution of T given V=v is normal with mean 0 a nd variance v . b. Use (a) to find the joint probability density function of (T,V). c. Integrate the joint probability density function in (b) with respect to v to find the probability density function of T. The distribution of T is known as the Student t distribution with n degree of freedom. The distribution is well defined for any n > 0, but in practice, only positive integer values of n are of interest. This distribution was first studied by William Gosset, who published under the pseudonym Student. In addition to supplying the proof, Exercise 1 provides a good way of thinking of the t distribution: the t distribution arises when the variance of a mean 0 normal distribution is randomized in a certain way.
    [Show full text]
  • Randomized Algorithms
    Chapter 9 Randomized Algorithms randomized The theme of this chapter is madendrizo algorithms. These are algorithms that make use of randomness in their computation. You might know of quicksort, which is efficient on average when it uses a random pivot, but can be bad for any pivot that is selected without randomness. Analyzing randomized algorithms can be difficult, so you might wonder why randomiza- tion in algorithms is so important and worth the extra effort. Well it turns out that for certain problems randomized algorithms are simpler or faster than algorithms that do not use random- ness. The problem of primality testing (PT), which is to determine if an integer is prime, is a good example. In the late 70s Miller and Rabin developed a famous and simple random- ized algorithm for the problem that only requires polynomial work. For over 20 years it was not known whether the problem could be solved in polynomial work without randomization. Eventually a polynomial time algorithm was developed, but it is much more complicated and computationally more costly than the randomized version. Hence in practice everyone still uses the randomized version. There are many other problems in which a randomized solution is simpler or cheaper than the best non-randomized solution. In this chapter, after covering the prerequisite background, we will consider some such problems. The first we will consider is the following simple prob- lem: Question: How many comparisons do we need to find the top two largest numbers in a sequence of n distinct numbers? Without the help of randomization, there is a trivial algorithm for finding the top two largest numbers in a sequence that requires about 2n − 3 comparisons.
    [Show full text]
  • Probability Cheatsheet V2.0 Thinking Conditionally Law of Total Probability (LOTP)
    Probability Cheatsheet v2.0 Thinking Conditionally Law of Total Probability (LOTP) Let B1;B2;B3; :::Bn be a partition of the sample space (i.e., they are Compiled by William Chen (http://wzchen.com) and Joe Blitzstein, Independence disjoint and their union is the entire sample space). with contributions from Sebastian Chiu, Yuan Jiang, Yuqi Hou, and Independent Events A and B are independent if knowing whether P (A) = P (AjB )P (B ) + P (AjB )P (B ) + ··· + P (AjB )P (B ) Jessy Hwang. Material based on Joe Blitzstein's (@stat110) lectures 1 1 2 2 n n A occurred gives no information about whether B occurred. More (http://stat110.net) and Blitzstein/Hwang's Introduction to P (A) = P (A \ B1) + P (A \ B2) + ··· + P (A \ Bn) formally, A and B (which have nonzero probability) are independent if Probability textbook (http://bit.ly/introprobability). Licensed and only if one of the following equivalent statements holds: For LOTP with extra conditioning, just add in another event C! under CC BY-NC-SA 4.0. Please share comments, suggestions, and errors at http://github.com/wzchen/probability_cheatsheet. P (A \ B) = P (A)P (B) P (AjC) = P (AjB1;C)P (B1jC) + ··· + P (AjBn;C)P (BnjC) P (AjB) = P (A) P (AjC) = P (A \ B1jC) + P (A \ B2jC) + ··· + P (A \ BnjC) P (BjA) = P (B) Last Updated September 4, 2015 Special case of LOTP with B and Bc as partition: Conditional Independence A and B are conditionally independent P (A) = P (AjB)P (B) + P (AjBc)P (Bc) given C if P (A \ BjC) = P (AjC)P (BjC).
    [Show full text]
  • A Tail Quantile Approximation Formula for the Student T and the Symmetric Generalized Hyperbolic Distribution
    A Service of Leibniz-Informationszentrum econstor Wirtschaft Leibniz Information Centre Make Your Publications Visible. zbw for Economics Schlüter, Stephan; Fischer, Matthias J. Working Paper A tail quantile approximation formula for the student t and the symmetric generalized hyperbolic distribution IWQW Discussion Papers, No. 05/2009 Provided in Cooperation with: Friedrich-Alexander University Erlangen-Nuremberg, Institute for Economics Suggested Citation: Schlüter, Stephan; Fischer, Matthias J. (2009) : A tail quantile approximation formula for the student t and the symmetric generalized hyperbolic distribution, IWQW Discussion Papers, No. 05/2009, Friedrich-Alexander-Universität Erlangen-Nürnberg, Institut für Wirtschaftspolitik und Quantitative Wirtschaftsforschung (IWQW), Nürnberg This Version is available at: http://hdl.handle.net/10419/29554 Standard-Nutzungsbedingungen: Terms of use: Die Dokumente auf EconStor dürfen zu eigenen wissenschaftlichen Documents in EconStor may be saved and copied for your Zwecken und zum Privatgebrauch gespeichert und kopiert werden. personal and scholarly purposes. Sie dürfen die Dokumente nicht für öffentliche oder kommerzielle You are not to copy documents for public or commercial Zwecke vervielfältigen, öffentlich ausstellen, öffentlich zugänglich purposes, to exhibit the documents publicly, to make them machen, vertreiben oder anderweitig nutzen. publicly available on the internet, or to distribute or otherwise use the documents in public. Sofern die Verfasser die Dokumente unter Open-Content-Lizenzen (insbesondere CC-Lizenzen) zur Verfügung gestellt haben sollten, If the documents have been made available under an Open gelten abweichend von diesen Nutzungsbedingungen die in der dort Content Licence (especially Creative Commons Licences), you genannten Lizenz gewährten Nutzungsrechte. may exercise further usage rights as specified in the indicated licence. www.econstor.eu IWQW Institut für Wirtschaftspolitik und Quantitative Wirtschaftsforschung Diskussionspapier Discussion Papers No.
    [Show full text]
  • Joint Probability Distributions
    ST 380 Probability and Statistics for the Physical Sciences Joint Probability Distributions In many experiments, two or more random variables have values that are determined by the outcome of the experiment. For example, the binomial experiment is a sequence of trials, each of which results in success or failure. If ( 1 if the i th trial is a success Xi = 0 otherwise; then X1; X2;:::; Xn are all random variables defined on the whole experiment. 1 / 15 Joint Probability Distributions Introduction ST 380 Probability and Statistics for the Physical Sciences To calculate probabilities involving two random variables X and Y such as P(X > 0 and Y ≤ 0); we need the joint distribution of X and Y . The way we represent the joint distribution depends on whether the random variables are discrete or continuous. 2 / 15 Joint Probability Distributions Introduction ST 380 Probability and Statistics for the Physical Sciences Two Discrete Random Variables If X and Y are discrete, with ranges RX and RY , respectively, the joint probability mass function is p(x; y) = P(X = x and Y = y); x 2 RX ; y 2 RY : Then a probability like P(X > 0 and Y ≤ 0) is just X X p(x; y): x2RX :x>0 y2RY :y≤0 3 / 15 Joint Probability Distributions Two Discrete Random Variables ST 380 Probability and Statistics for the Physical Sciences Marginal Distribution To find the probability of an event defined only by X , we need the marginal pmf of X : X pX (x) = P(X = x) = p(x; y); x 2 RX : y2RY Similarly the marginal pmf of Y is X pY (y) = P(Y = y) = p(x; y); y 2 RY : x2RX 4 / 15 Joint
    [Show full text]
  • The Probability Lifesaver: Order Statistics and the Median Theorem
    The Probability Lifesaver: Order Statistics and the Median Theorem Steven J. Miller December 30, 2015 Contents 1 Order Statistics and the Median Theorem 3 1.1 Definition of the Median 5 1.2 Order Statistics 10 1.3 Examples of Order Statistics 15 1.4 TheSampleDistributionoftheMedian 17 1.5 TechnicalboundsforproofofMedianTheorem 20 1.6 TheMedianofNormalRandomVariables 22 2 • Greetings again! In this supplemental chapter we develop the theory of order statistics in order to prove The Median Theorem. This is a beautiful result in its own, but also extremely important as a substitute for the Central Limit Theorem, and allows us to say non- trivial things when the CLT is unavailable. Chapter 1 Order Statistics and the Median Theorem The Central Limit Theorem is one of the gems of probability. It’s easy to use and its hypotheses are satisfied in a wealth of problems. Many courses build towards a proof of this beautiful and powerful result, as it truly is ‘central’ to the entire subject. Not to detract from the majesty of this wonderful result, however, what happens in those instances where it’s unavailable? For example, one of the key assumptions that must be met is that our random variables need to have finite higher moments, or at the very least a finite variance. What if we were to consider sums of Cauchy random variables? Is there anything we can say? This is not just a question of theoretical interest, of mathematicians generalizing for the sake of generalization. The following example from economics highlights why this chapter is more than just of theoretical interest.
    [Show full text]
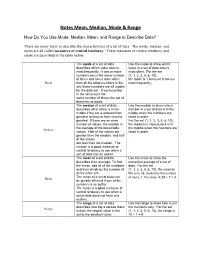
  • Notes Mean, Median, Mode & Range
    Notes Mean, Median, Mode & Range How Do You Use Mode, Median, Mean, and Range to Describe Data? There are many ways to describe the characteristics of a set of data. The mode, median, and mean are all called measures of central tendency. These measures of central tendency and range are described in the table below. The mode of a set of data Use the mode to show which describes which value occurs value in a set of data occurs most frequently. If two or more most often. For the set numbers occur the same number {1, 1, 2, 3, 5, 6, 10}, of times and occur more often the mode is 1 because it occurs Mode than all the other numbers in the most frequently. set, those numbers are all modes for the data set. If each number in the set occurs the same number of times, the set of data has no mode. The median of a set of data Use the median to show which describes what value is in the number in a set of data is in the middle if the set is ordered from middle when the numbers are greatest to least or from least to listed in order. greatest. If there are an even For the set {1, 1, 2, 3, 5, 6, 10}, number of values, the median is the median is 3 because it is in the average of the two middle the middle when the numbers are Median values. Half of the values are listed in order. greater than the median, and half of the values are less than the median.
    [Show full text]
  • Functions of Random Variables
    Names for Eg(X ) Generating Functions Topic 8 The Expected Value Functions of Random Variables 1 / 19 Names for Eg(X ) Generating Functions Outline Names for Eg(X ) Means Moments Factorial Moments Variance and Standard Deviation Generating Functions 2 / 19 Names for Eg(X ) Generating Functions Means If g(x) = x, then µX = EX is called variously the distributional mean, and the first moment. • Sn, the number of successes in n Bernoulli trials with success parameter p, has mean np. • The mean of a geometric random variable with parameter p is (1 − p)=p . • The mean of an exponential random variable with parameter β is1 /β. • A standard normal random variable has mean0. Exercise. Find the mean of a Pareto random variable. Z 1 Z 1 βαβ Z 1 αββ 1 αβ xf (x) dx = x dx = βαβ x−β dx = x1−β = ; β > 1 x β+1 −∞ α x α 1 − β α β − 1 3 / 19 Names for Eg(X ) Generating Functions Moments In analogy to a similar concept in physics, EX m is called the m-th moment. The second moment in physics is associated to the moment of inertia. • If X is a Bernoulli random variable, then X = X m. Thus, EX m = EX = p. • For a uniform random variable on [0; 1], the m-th moment is R 1 m 0 x dx = 1=(m + 1). • The third moment for Z, a standard normal random, is0. The fourth moment, 1 Z 1 z2 1 z2 1 4 4 3 EZ = p z exp − dz = −p z exp − 2π −∞ 2 2π 2 −∞ 1 Z 1 z2 +p 3z2 exp − dz = 3EZ 2 = 3 2π −∞ 2 3 z2 u(z) = z v(t) = − exp − 2 0 2 0 z2 u (z) = 3z v (t) = z exp − 2 4 / 19 Names for Eg(X ) Generating Functions Factorial Moments If g(x) = (x)k , where( x)k = x(x − 1) ··· (x − k + 1), then E(X )k is called the k-th factorial moment.
    [Show full text]
  • Sampling Student's T Distribution – Use of the Inverse Cumulative
    Sampling Student’s T distribution – use of the inverse cumulative distribution function William T. Shaw Department of Mathematics, King’s College, The Strand, London WC2R 2LS, UK With the current interest in copula methods, and fat-tailed or other non-normal distributions, it is appropriate to investigate technologies for managing marginal distributions of interest. We explore “Student’s” T distribution, survey its simulation, and present some new techniques for simulation. In particular, for a given real (not necessarily integer) value n of the number of degrees of freedom, −1 we give a pair of power series approximations for the inverse, Fn ,ofthe cumulative distribution function (CDF), Fn.Wealsogivesomesimpleandvery fast exact and iterative techniques for defining this function when n is an even −1 integer, based on the observation that for such cases the calculation of Fn amounts to the solution of a reduced-form polynomial equation of degree n − 1. We also explain the use of Cornish–Fisher expansions to define the inverse CDF as the composition of the inverse CDF for the normal case with a simple polynomial map. The methods presented are well adapted for use with copula and quasi-Monte-Carlo techniques. 1 Introduction There is much interest in many areas of financial modeling on the use of copulas to glue together marginal univariate distributions where there is no easy canonical multivariate distribution, or one wishes to have flexibility in the mechanism for combination. One of the more interesting marginal distributions is the “Student’s” T distribution. This statistical distribution was published by W. Gosset in 1908.
    [Show full text]