DOCSLIB.ORG

Hyperbolas 753

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Hyperbolas 753 333202_1004.qxd 12/8/05 9:03 AM Page 753 Section 10.4 Hyperbolas 753 10.4 Hyperbolas What you should learn •Write equations of hyperbolas Introduction in standard form. The third type of conic is called a hyperbola. The definition of a hyperbola is •Find asymptotes of and graph similar to that of an ellipse. The difference is that for an ellipse the sum of the hyperbolas. distances between the foci and a point on the ellipse is fixed, whereas for a •Use properties of hyperbolas hyperbola the difference of the distances between the foci and a point on the to solve real-life problems. hyperbola is fixed. •Classify conics from their general equations. Definition of Hyperbola Why you should learn it A hyperbola is the set of all points ͑x, y͒ in a plane, the difference of whose Hyperbolas can be used to distances from two distinct fixed points (foci) is a positive constant. See model and solve many types of Figure 10.29. real-life problems. For instance, in Exercise 42 on page 761, hyperbolas are used in long c distance radio navigation for (,x y ) Brancha Branch d aircraft and ships. 2 d1 Vertex Focus Focus Center Vertex Transverse axis − dd21is a positive constant. FIGURE 10.29 FIGURE 10.30 The graph of a hyperbola has two disconnected branches. The line through the two foci intersects the hyperbola at its two vertices. The line segment connecting the vertices is the transverse axis, and the midpoint of the transverse axis is the center of the hyperbola. See Figure 10.30. The development of the standard form of the equation of a hyperbola is similar to that of an ellipse. Note in the definition below that a, b, and c are related differently for hyperbolas than AP/Wide World Photos for ellipses. Standard Equation of a Hyperbola The standard form of the equation of a hyperbola with center ͑h, k͒ is ͑x Ϫ h͒2 ͑ y Ϫ k͒2 Ϫ ϭ 1 Transverse axis is horizontal. a 2 b2 ͑ y Ϫ k͒ 2 ͑x Ϫ h͒2 Ϫ ϭ 1. Transverse axis is vertical. a2 b 2 The vertices are a units from the center, and the foci are c units from the center. Moreover,c 2 ϭ a2 ϩ b2. If the center of the hyperbola is at the origin ͑0, 0͒, the equation takes one of the following forms. x 2 y 2 Transverse axis y 2 x 2 Transverse axis Ϫ ϭ 1 Ϫ ϭ 1 is vertical. a2 b2 is horizontal. a2 b2 333202_1004.qxd 12/8/05 9:03 AM Page 754 754 Chapter 10 Topics in Analytic Geometry Figure 10.31 shows both the horizontal and vertical orientations for a hyperbola. ()xh− 22()yk− ()yk− 22()xh− − = 1 − = 1 ab22 ab22 y y (,h k + c ) (,)hc− k (,h k ) (+,)hc k (,h k ) x x (,h k− c ) Transverse axis is horizontal. Transverse axis is vertical. FIGURE 10.31 Example 1 Finding the Standard Equation of a Hyperbola Find the standard form of the equation of the hyperbola with foci ͑Ϫ1, 2͒ and ͑5, 2͒ and vertices ͑0, 2͒ and ͑4, 2͒. When finding the standard form Solution of the equation of any conic, By the Midpoint Formula, the center of the hyperbola occurs at the point ͑2, 2͒. it is helpful to sketch a graph Furthermore,c ϭ 5 Ϫ 2 ϭ 3 and a ϭ 4 Ϫ 2 ϭ 2, and it follows that of the conic with the given b ϭ Ίc2 Ϫ a2 ϭ Ί 2 Ϫ 2 ϭ Ί Ϫ ϭ Ί characteristics. 3 2 9 4 5. So, the hyperbola has a horizontal transverse axis and the standard form of the equation is ͑x Ϫ 2͒2 ͑y Ϫ 2͒2 Ϫ ϭ 1. See Figure 10.32. 22 ͑Ί5͒2 This equation simplifies to ͑x Ϫ 2͒2 ͑y Ϫ 2͒2 Ϫ ϭ 1. 4 5 (x − 2)2 (y − 2)2 − = 1 y 22 ( 5 ( 2 5 4 (0, 2) (4, 2) (2, 2) (−1, 2) (5, 2) x 123 4 −1 FIGURE 10.32 Now try Exercise 27. 333202_1004.qxd 12/8/05 9:03 AM Page 755 Section 10.4 Hyperbolas 755 Conjugate Asymptotes of a Hyperbola axis Each hyperbola has two asymptotes that intersect at the center of the hyperbola, (h, k + b) Asymptote as shown in Figure 10.33. The asymptotes pass through the vertices of a rectangle of dimensions 2a by 2b, with its center at ͑h, k͒. The line segment of length 2b joining ͑h, k ϩ b͒ and ͑h, k Ϫ b͒ ͓or ͑h ϩ b, k͒ and ͑h Ϫ b, k͔͒ is the conjugate (h, k) axis of the hyperbola. Asymptotes of a Hyperbola (h, k − b) Asymptote The equations of the asymptotes of a hyperbola are − + b (h a, k) (h a, k) y ϭ k ± ͑x Ϫ h͒ Transverse axis is horizontal. a FIGURE 10.33 a y ϭ k ± ͑x Ϫ h͒. Transverse axis is vertical. b Example 2 Using Asymptotes to Sketch a Hyperbola Sketch the hyperbola whose equation is 4x 2 Ϫ y 2 ϭ 16. Solution Divide each side of the original equation by 16, and rewrite the equation in standard form. x 2 y 2 Ϫ ϭ 1 Write in standard form. 22 42 From this, you can conclude that a ϭ 2, b ϭ 4, and the transverse axis is hori- zontal. So, the vertices occur at ͑Ϫ2, 0͒ and ͑2, 0͒, and the endpoints of the con- jugate axis occur at ͑0, Ϫ4͒ and ͑0, 4͒. Using these four points, you are able to sketch the rectangle shown in Figure 10.34. Now, from c2 ϭ a2 ϩ b2, you have c ϭ Ί22 ϩ 42 ϭ Ί20 ϭ 2Ί5. So, the foci of the hyperbola are ͑Ϫ2Ί5, 0͒ and ͑2Ί5, 0͒. Finally, by drawing the asymptotes through the corners of this rec- tangle, you can complete the sketch shown in Figure 10.35. Note that the asymp- totes are y ϭ 2x and y ϭϪ2x. y y 8 8 (0, 4) 6 6 (−2, 0) (2, 0) (− 2 5, 0 ) (2 5, 0 ) x x −6 −4 46 −6 −4 46 xy22 − = 1 22 42 (0,− 4) −6 −6 FIGURE 10.34 FIGURE 10.35 Now try Exercise 7. 333202_1004.qxd 12/8/05 11:22 AM Page 756 756 Chapter 10 Topics in Analytic Geometry Example 3 Finding the Asymptotes of a Hyperbola Sketch the hyperbola given by 4x 2 Ϫ 3y 2 ϩ 8x ϩ 16 ϭ 0 and find the equations of its asymptotes and the foci. Solution 4 x 2 Ϫ 3y 2 ϩ 8x ϩ 16 ϭ 0 Write original equation. ͑4x2 ϩ 8x͒ Ϫ 3y2 ϭϪ16 Group terms. 4 ͑x 2 ϩ 2x͒ Ϫ 3y 2 ϭϪ16 Factor 4 from x-terms. 4͑x 2 ϩ 2x ϩ 1͒ Ϫ 3y 2 ϭϪ16 ϩ 4 Add 4 to each side. 4 ͑x ϩ 1͒2 Ϫ 3y 2 ϭϪ12 Write in completed square form. ͑x ϩ 1͒2 y2 Ϫ ϩ ϭ 1 Divide each side by Ϫ12. 3 4 y 2 ͑x ϩ 1͒2 y Ϫ ϭ 1 Write in standard form. 22 ͑Ί3͒2 (− 1, 2 + 7 ) From this equation you can conclude that the hyperbola has a vertical transverse (−1, 2) 4 ͑Ϫ ͒ ͑Ϫ ͒ ͑Ϫ Ϫ ͒ 3 axis, centered at 1, 0 , has vertices 1, 2 and 1, 2 , and has a conjugate y2 (x + 1)2 axis with endpoints ͑Ϫ1 Ϫ Ί3, 0͒ and ͑Ϫ1 ϩ Ί3, 0͒. To sketch the hyperbola, − = 1 (−1, 0) 1 22 ( 3 )2 draw a rectangle through these four points. The asymptotes are the lines passing x through the corners of the rectangle. Using a ϭ 2 and b ϭ Ί3, you can −4 −3 −2 12345 conclude that the equations of the asymptotes are 2 2 − y ϭ ͑x ϩ 1͒ and y ϭ Ϫ ͑x ϩ 1͒. 3 Ί Ί (−1, −2) 3 3 Finally, you can determine the foci by using the equation c2 ϭ a2 ϩ b2. So, you (− 1, − 2 − 7 ) have c ϭ Ί22 ϩ ͑Ί3͒2 ϭ Ί7, and the foci are ͑Ϫ1, Ϫ2 Ϫ Ί7͒ and FIGURE 10.36 ͑Ϫ1, Ϫ2 ϩ Ί7͒. The hyperbola is shown in Figure 10.36. Now try Exercise 13. Technology You can use a graphing utility to graph a hyperbola by graphing the upper and lower portions in the same viewing window. For instance, to graph the hyperbola in Example 3, first solve for y to get ͑ ϩ ͒2 ͑x ϩ 1͒2 ϭ ϩ x 1 ϭϪ ϩ y 2Ί1 and y2 2Ί1 . 1 3 3 Use a viewing window in which Ϫ9 ≤ x ≤ 9 and Ϫ6 ≤ y ≤ 6. You should obtain the graph shown below. Notice that the graphing utility does not draw the asymptotes. However, if you trace along the branches, you will see that the values of the hyperbola approach the asymptotes. 6 −99 −6 333202_1004.qxd 12/8/05 9:03 AM Page 757 Section 10.4 Hyperbolas 757 y y = 2x − 8 Example 4 Using Asymptotes to Find the Standard Equation Find the standard form of the equation of the hyperbola having vertices ͑3, Ϫ5͒ 2 (3, 1) and ͑3, 1͒ and having asymptotes x y ϭ 2x Ϫ 8 and y ϭϪ2x ϩ 4 −2 264 as shown in Figure 10.37. −2 Solution −4 By the Midpoint Formula, the center of the hyperbola is ͑3, Ϫ2͒. Furthermore, the (3, −5) hyperbola has a vertical transverse axis with a ϭ 3.
Load more

Recommended publications
  • Device Constructions with Hyperbolas
    Device Constructions with Hyperbolas Alfonso Croeze1 William Kelly1 William Smith2 1Department of Mathematics Louisiana State University Baton Rouge, LA 2Department of Mathematics University of Mississippi Oxford, MS July 8, 2011 Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas Hyperbola Definition Conic Section Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas Hyperbola Definition Conic Section Two Foci Focus and Directrix Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas The Project Basic constructions Constructing a Hyperbola Advanced constructions Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas Rusty Compass Theorem Given a circle centered at a point A with radius r and any point C different from A, it is possible to construct a circle centered at C that is congruent to the circle centered at A with a compass and straightedge. Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas X B C A Y Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas X D B C A Y Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas A B X Y Angle Duplication A X Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas Angle Duplication A X A B X Y Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas C Z A B X Y C Z A B X Y Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas C Z A B X Y C Z A B X Y Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas Constructing a Perpendicular C C A B Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas C C X X O A B A B Y Y Croeze, Kelly, Smith LSU&UoM Device Constructions with Hyperbolas We needed a way to draw a hyperbola.
    [Show full text]
  • Apollonius of Pergaconics. Books One - Seven
    APOLLONIUS OF PERGACONICS. BOOKS ONE - SEVEN INTRODUCTION A. Apollonius at Perga Apollonius was born at Perga (Περγα) on the Southern coast of Asia Mi- nor, near the modern Turkish city of Bursa. Little is known about his life before he arrived in Alexandria, where he studied. Certain information about Apollonius’ life in Asia Minor can be obtained from his preface to Book 2 of Conics. The name “Apollonius”(Apollonius) means “devoted to Apollo”, similarly to “Artemius” or “Demetrius” meaning “devoted to Artemis or Demeter”. In the mentioned preface Apollonius writes to Eudemus of Pergamum that he sends him one of the books of Conics via his son also named Apollonius. The coincidence shows that this name was traditional in the family, and in all prob- ability Apollonius’ ancestors were priests of Apollo. Asia Minor during many centuries was for Indo-European tribes a bridge to Europe from their pre-fatherland south of the Caspian Sea. The Indo-European nation living in Asia Minor in 2nd and the beginning of the 1st millennia B.C. was usually called Hittites. Hittites are mentioned in the Bible and in Egyptian papyri. A military leader serving under the Biblical king David was the Hittite Uriah. His wife Bath- sheba, after his death, became the wife of king David and the mother of king Solomon. Hittites had a cuneiform writing analogous to the Babylonian one and hi- eroglyphs analogous to Egyptian ones. The Czech historian Bedrich Hrozny (1879-1952) who has deciphered Hittite cuneiform writing had established that the Hittite language belonged to the Western group of Indo-European languages [Hro].
    [Show full text]
  • 14. Mathematics for Orbits: Ellipses, Parabolas, Hyperbolas Michael Fowler
    14. Mathematics for Orbits: Ellipses, Parabolas, Hyperbolas Michael Fowler Preliminaries: Conic Sections Ellipses, parabolas and hyperbolas can all be generated by cutting a cone with a plane (see diagrams, from Wikimedia Commons). Taking the cone to be xyz222+=, and substituting the z in that equation from the planar equation rp⋅= p, where p is the vector perpendicular to the plane from the origin to the plane, gives a quadratic equation in xy,. This translates into a quadratic equation in the plane—take the line of intersection of the cutting plane with the xy, plane as the y axis in both, then one is related to the other by a scaling xx′ = λ . To identify the conic, diagonalized the form, and look at the coefficients of xy22,. If they are the same sign, it is an ellipse, opposite, a hyperbola. The parabola is the exceptional case where one is zero, the other equates to a linear term. It is instructive to see how an important property of the ellipse follows immediately from this construction. The slanting plane in the figure cuts the cone in an ellipse. Two spheres inside the cone, having circles of contact with the cone CC, ′, are adjusted in size so that they both just touch the plane, at points FF, ′ respectively. It is easy to see that such spheres exist, for example start with a tiny sphere inside the cone near the point, and gradually inflate it, keeping it spherical and touching the cone, until it touches the plane. Now consider a point P on the ellipse.
    [Show full text]
  • 2.3 Conic Sections: Hyperbola ( ) ( ) ( )
    2.3 Conic Sections: Hyperbola Hyperbola (locus definition) Set of all points (x, y) in the place such that the absolute value of the difference of each distances from F1 and F2 to (x, y) is a constant distance, d. In the figure above: The distance from F1 to (x1, y1 ) - the distance from F2 to (x1, y1 ) = d and The distance from F1 to (x2 , y2 ) - the distance from F2 to (x2 , y2 ) = d Standard Form of a Hyperbola: Horizontal Hyperbola Vertical Hyperbola 2 2 2 2 (x − h) (y − k) (y − k) (x − h) 2 − 2 = 1 2 − 2 = 1 a b a b center = (h,k) 2a = distance between vertices c = distance from center to focus c2 = a2 + b2 c eccentricity e = ( e > 1 for a hyperbola) a Conjugate axis = 2b Transverse axis = 2a Horizontal Asymptotes Vertical Asymptotes b a y − k = ± (x − h) y − k = ± (x − h) a b Show how d = 2a 2 (x − 2) y2 Ex. Graph − = 1 4 25 Center: (2, 0) Vertices (4, 0) & (0, 0) Foci (2 ± 29,0) 5 Asymptotes: y = ± (x − 2) 2 Ex. Graph 9y2 − x2 − 6x −10 = 0 9y2 − x2 − 6x = 10 9y2 −1(x2 + 6x + 9) = 10 − 9 2 9y2 −1(x + 3) = 1 2 9y2 1(x + 3) 1 − = 1 1 1 2 y2 x + 3 ( ) 1 1 − = 9 1 Center: (-3, 0) ⎛ 1⎞ ⎛ 1⎞ Vertices −3, & −3,− ⎝⎜ 3⎠⎟ ⎝⎜ 3⎠⎟ ⎛ 10 ⎞ Foci −3,± ⎝⎜ 3 ⎠⎟ 1 Asymptotes: y = ± (x + 3) 3 Hyperbolas can be used in so-called ‘trilateration’ or ‘positioning’ problems. The procedure outlined in the next example is the basis of the Long Range Aid to Navigation (LORAN) system, (outdated now due to GPS) Ex.
    [Show full text]
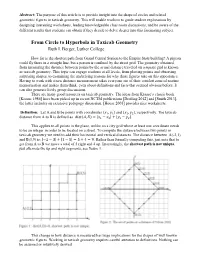
  • From Circle to Hyperbola in Taxicab Geometry
    Abstract: The purpose of this article is to provide insight into the shape of circles and related geometric figures in taxicab geometry. This will enable teachers to guide student explorations by designing interesting worksheets, leading knowledgeable class room discussions, and be aware of the different results that students can obtain if they decide to delve deeper into this fascinating subject. From Circle to Hyperbola in Taxicab Geometry Ruth I. Berger, Luther College How far is the shortest path from Grand Central Station to the Empire State building? A pigeon could fly there in a straight line, but a person is confined by the street grid. The geometry obtained from measuring the distance between points by the actual distance traveled on a square grid is known as taxicab geometry. This topic can engage students at all levels, from plotting points and observing surprising shapes, to examining the underlying reasons for why these figures take on this appearance. Having to work with a new distance measurement takes everyone out of their comfort zone of routine memorization and makes them think, even about definitions and facts that seemed obvious before. It can also generate lively group discussions. There are many good resources on taxicab geometry. The ideas from Krause’s classic book [Krause 1986] have been picked up in recent NCTM publications [Dreiling 2012] and [Smith 2013], the latter includes an extensive pedagogy discussion. [House 2005] provides nice worksheets. Definition: Let A and B be points with coordinates (푥1, 푦1) and (푥2, 푦2), respectively. The taxicab distance from A to B is defined as 푑푖푠푡(퐴, 퐵) = |푥1 − 푥2| + |푦1 − 푦2|.
    [Show full text]
  • Ellipse, Hyperbola and Their Conjunction Arxiv:1805.02111V2
    Ellipse, Hyperbola and Their Conjunction Arkadiusz Kobiera Warsaw University of Technology Abstract This article presents a simple analysis of cones which are used to generate a given conic curve by section by a plane. It was found that if the given curve is an ellipse, then the locus of vertices of the cones is a hyperbola. The hyperbola has foci which coincidence with the ellipse vertices. Similarly, if the given curve is the hyperbola, the locus of vertex of the cones is the ellipse. In the second case, the foci of the ellipse are located in the hyperbola's vertices. These two relationships create a kind of conjunction between the ellipse and the hyperbola which originate from the cones used for generation of these curves. The presented conjunction of the ellipse and hyperbola is a perfect example of mathematical beauty which may be shown by the use of very simple geometry. As in the past the conic curves appear to be arXiv:1805.02111v2 [math.HO] 26 Jan 2019 very interesting and fruitful mathematical beings. 1 Introduction The conical curves are mathematical entities which have been known for thousands years since the first Menaechmus' research around 250 B.C. [2]. Anybody who has attempted undergraduate course of geometry knows that ellipse, hyperbola and parabola are obtained by section of a cone by a plane. Every book dealing with the this subject has a sketch where the cone is sec- tioned by planes at various angles, which produces different kinds of conics. Usually authors start with the cone to produce the conic curve by section.
    [Show full text]
  • Section 9.2 Hyperbolas 597
    Section 9.2 Hyperbolas 597 Section 9.2 Hyperbolas In the last section, we learned that planets have approximately elliptical orbits around the sun. When an object like a comet is moving quickly, it is able to escape the gravitational pull of the sun and follows a path with the shape of a hyperbola. Hyperbolas are curves that can help us find the location of a ship, describe the shape of cooling towers, or calibrate seismological equipment. The hyperbola is another type of conic section created by intersecting a plane with a double cone, as shown below5. The word “hyperbola” derives from a Greek word meaning “excess.” The English word “hyperbole” means exaggeration. We can think of a hyperbola as an excessive or exaggerated ellipse, one turned inside out. We defined an ellipse as the set of all points where the sum of the distances from that point to two fixed points is a constant. A hyperbola is the set of all points where the absolute value of the difference of the distances from the point to two fixed points is a constant. 5 Pbroks13 (https://commons.wikimedia.org/wiki/File:Conic_sections_with_plane.svg), “Conic sections with plane”, cropped to show only a hyperbola by L Michaels, CC BY 3.0 598 Chapter 9 Hyperbola Definition A hyperbola is the set of all points Q (x, y) for which the absolute value of the difference of the distances to two fixed points F1(x1, y1) and F2 (x2, y2 ) called the foci (plural for focus) is a constant k: d(Q, F1 )− d(Q, F2 ) = k .
    [Show full text]
  • Lecture 11. Apollonius and Conic Sections
    Lecture 11. Apollonius and Conic Sections Figure 11.1 Apollonius of Perga Apollonius of Perga Apollonius (262 B.C.-190 B.C.) was born in the Greek city of Perga, close to the southeast coast of Asia Minor. He was a Greek geometer and astronomer. His major mathematical work on the theory of conic sections had a very great influence on the development of mathematics and his famous book Conics introduced the terms parabola, ellipse and hyperbola. Apollonius' theory of conics was so admired that it was he, rather than Euclid, who in antiquity earned the title the Great Geometer. He also made contribution to the study of the Moon. The Apollonius crater on the Moon was named in his honor. Apollonius came to Alexandria in his youth and learned mathematics from Euclid's successors. As far as we know he remained in Alexandria and became an associate among the great mathematicians who worked there. We do not know much details about his life. His chief work was on the conic sections but he also wrote on other subjects. His mathematical powers were so extraordinary that he became known in his time. His reputation as an astronomer was also great. Apollonius' mathematical works Apollonius is famous for his work, the Conic, which was spread out over eight books and contained 389 propositions. The first four books were 69 in the original Greek language, the next three are preserved in Arabic translations, while the last one is lost. Even though seven of the eight books of the Conics have survived, most of his mathematical work is known today only by titles and summaries in works of later authors.
    [Show full text]
  • High School Mathematics Glossary Pre-Calculus
    High School Mathematics Glossary Pre-calculus English-Chinese BOARD OF EDUCATION OF THE CITY OF NEW YORK Board of Education of the City of New York Carol A. Gresser President Irene H. ImpeUizzeri Vice President Louis DeSario Sandra E. Lerner Luis O. Reyes Ninfa Segarra-Velez William C. Thompson, ]r. Members Tiffany Raspberry Student Advisory Member Ramon C. Cortines Chancellor Beverly 1. Hall Deputy Chancellor for Instruction 3195 Ie is the: policy of the New York City Board of Education not to discriminate on (he basis of race. color, creed. religion. national origin. age. handicapping condition. marital StatuS • .saual orientation. or sex in itS eduacional programs. activities. and employment policies. AS required by law. Inquiries regarding compiiulce with appropriate laws may be directed to Dr. Frederick..6,.. Hill. Director (Acting), Dircoetcr, Office of Equal Opporrurury. 110 Livingston Screet. Brooklyn. New York 11201: or Director. Office for o ..·ij Rights. Depa.rtmenc of Education. 26 Federal PJaz:t. Room 33- to. New York. 'Ne:w York 10278. HIGH SCHOOL MATHEMATICS GLOSSARY PRE-CALCULUS ENGLISH - ClllNESE ~ 0/ * ~l.tt Jf -taJ ~ 1- -jJ)f {it ~t ~ -ffi 'ff Chinese!Asian Bilingual Education Technical Assistance Center Division of Bilingual Education Board of Education of the City of New York 1995 INTRODUCTION The High School English-Chinese Mathematics Glossary: Pre­ calculus was developed to assist the limited English proficient Chinese high school students in understanding the vocabulary that is included in the New York City High School Pre-calculus curricu lum. To meet the needs of the Chinese students from different regions, both traditional and simplified character versions are included.
    [Show full text]
  • II Apollonius of Perga
    4. Alexandrian mathematics after Euclid — I I Due to the length of this unit , it has been split into three parts . Apollonius of Perga If one initiates a Google search of the Internet for the name “Apollonius ,” it becomes clear very quickly that many important contributors to Greek knowledge shared this name (reportedtly there are 193 different persons of this name cited in Pauly-Wisowa , Real-Enzyklopädie der klassischen Altertumswissenschaft ), and therefore one must pay particular attention to the full name in this case . The MacTutor article on Apollonius of Perga lists several of the more prominent Greek scholars with the same name . Apollonius of Perga made numerous contributions to mathematics (Perga was a city on the southwest /south central coast of Asia Minor) . As is usual for the period , many of his writings are now lost , but it is clear that his single most important achievement was an eight book work on conic sections , which begins with a general treatment of such curves and later goes very deeply into some of their properties . His work was extremely influential ; in particular , efforts to analyze his results played a very important role in the development of analytic geometry and calculus during the 17 th century . Background discussion of conics We know that students from Plato ’s Academy began studying conics during the 4th century B.C.E. , and one early achievement in the area was the use of intersecting parabolas by Manaechmus (380 – 320 B.C.E. , the brother of Dinostratus , who was mentioned in an earlier unit) to duplicate a cube (recall Exercise 4 on page 128 of Burton).
    [Show full text]
  • Analytic Geometry: the Conic Sections
    Analytic Geometry: The Conic Sections It is impossible not to feel stirred at the “thought of the emotions of men at certain historic moments of adventure and discovery. Such moments are also granted to students in the abstract regions of thought, and high among them must be placed the morning when Descartes lay in bed and invented the method of coordinate geometry. —Alfred N”orth Whitehead 12.1 The Distance and Midpoint Formulas 12.2 Symmetry 12.3 The Circle 12.4 The Parabola 12.5 The Ellipse and the Hyperbola 12.6 Identifying the Conic Sections When NASA scientists want to launch a probe to study the planets of our solar system, how do they plot the path of the probe through space? For example, the Voyager probe (which discovered the presence of active volcanoes on the moon Io) crashed into the giant planet Jupiter after traveling almost three billion miles! How did NASA scientists know where Jupiter would be when the probe arrived? Scientists can accurately predict the location of any planet in our solar system at any future time because they know that the planets follow elliptical orbits around the Sun. In fact, 441 442 Chapter 12 I Analytic Geometry: The Conic Sections the Sun is one of the two foci of each ellipse. An ellipse can look a lot like a circle, or it can appear longer and flatter. Which planets in our solar system have orbits which are most nearly circular? In this chapter’s project, you will http://www.jpl.nasa.gov/ learn how to answer that question.
    [Show full text]
  • 12.1 Parabolas 12.2 Circles 12.3 Ellipses 12.4 Hyperbolas
    8422d_c12_946-970 6/6/02 6:17 PM Page 946 mac85 Mac 85:365_smm:8422d_Thomasson: 12.1 Parabolas 12.2 Circles 12.3 Ellipses 12.4 Hyperbolas 8422d_c12_946-970 6/6/02 6:18 PM Page 947 mac85 Mac 85:365_smm:8422d_Thomasson: Chapter mooth, regular curves are common in the world around us. The orbit of the space shuttle around the SEarth is one kind of smooth curve; another is the shape of domed buildings such as the United States Capitol. Conic Television receiving dishes are a very common curved shape, as are the curved rearview mirrors on your car. Sections Mathematically, however, an interesting property of all the curves just mentioned is that they are expressed as qua- dratic equations in two variables. We discussed quadratic equations in Chapter 5. In the current chapter, we extend that discussion to other forms of equations and their related graphs, called conic sections: parabolas, circles, ellipses, and hyperbolas. We will describe each curve and analyze the equation used to graph it. We will also discuss properties that make these curves so use- ful in so many different areas, from engineering to archi- tecture to astronomy. We conclude the chapter with a project that further explores the various conic sections we have studied. 12.1 APPLICATION A satellite dish receiver is in the shape of a parabola. A cross section of the dish shows a diameter of 13 feet at a distance of 2.5 feet from the vertex of the parabola. Write an equation for the parabola. After completing this section, we will discuss this application fur- ther.
    [Show full text]