DOCSLIB.ORG

TN 2 – Basic Calculus with Finance [2016-09-03] Page 1 of 16

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
TN 2 – Basic Calculus with Finance [2016-09-03] Page 1 of 16 © G.S. Questa, 2016 TN 2 – Basic Calculus with Finance [2016-09-03] Page 1 of 16 TN 2 - Basic Calculus with Financial Applications 1 Functions and Limits 2 Derivatives 3 Taylor Series 4 Maxima and Minima 5 The Logarithmic and Exponential Functions 6 Linearity and Convexity. Gains from Convexity 7 Integrals 8 Log Yields (Continuously Compounded Yields) Glossary Excel Functions: EXP, LN Notation y fx() d y' f '() x fx () dx f() x f '() x dx Foreword Calculus can be considered as the mathematics of motion and change. It is a BIG topic with applications spanning the natural sciences and also some social sciences such as economics and finance. In this TN we can only review a few basic concepts that are most likely to be useful for some finance-oriented modules of Master courses. The discussion will be conducted with exclusive reference to real-valued univariate calculus (calculus of one variable) to benefit from its analytical simplicity and ease of visualization. §1 Functions and Limits The first use of the word function is credited to Leibniz (1646-1716). Until the mid-1800s the concept of function was that of a relatively straightforward mathematical formula expressing the relationship between the values of a dependent variable ()y and those of one or more independent variables (univariate and multivariate calculus). In the 19th century, the concepts of function and limit were generalized and made a lot more rigorous, thereby providing a solid foundation for the further development of calculus. A real-valued mathematical expression, such as the quadratic function in exhibit 1.1, has no defined numerical value until you assign a value to()x . Thus, we say that ()y is a function of ()x . Functions are also called transformations because they transform the value of()x into a value of()y . A very important element in the definition of a function is the requirement that for every given point on its domain (x-axis) there is one and only one function value. In other words, if you draw a straight line parallel to the y-axis it must cross only once the function’s graph. © G.S. Questa, 2016 TN 2 – Basic Calculus with Finance [2016-09-03] Page 2 of 16 Thus, if there is more than one value of ()y corresponding to one value of ()x we are dealing with two or more functions instead of one (see exhibit 1.2). 8 y yx -2 0.252 6 4 2 0 x -2 -8 -6 -4 -2 0 2 4 6 8 Exhibit 1.1 - Graph of the quadratic function 1 0.5 0 -0.5 -1 -1.5 -1.0 -0.5 0.0 0.5 1.0 1.5 Exhibit 1.2 - Graph of unit circle (radius = 1). This is composed by two functions: one for the positive values of (y) and one for the negative. Limits The concept of limit is now all-pervasive in calculus and its applications. The rigorous definition of the limit of a function was worked out in the mid-1800s. There are several types of limits. However, we shall concentrate only on two, chosen for their relevance for our studies. FIRST, the limit of a function that tends to zero for()x 0 , where the symbol () stand for “approaches”. This limit is the cornerstone for the definition and calculation of the derivative of a function and will be discussed in §2. limfx ( ) 0 x 0 SECOND, the limit of a function that tends to zero for()x . limfx ( ) 0 x The above limit is true if, given an arbitrarily small number (ε), there is a number (δ) such that: © G.S. Questa, 2016 TN 2 – Basic Calculus with Finance [2016-09-03] Page 3 of 16 x fx() 0 In other words, there is always a value (δ) large enough to obtain the desired result. This is also known as the (, ) approach. Zero Coupon Bond Example Consider the price ()Z of a zero coupon bond due in ()T years, given a constant compounded yield rate(Y 6 %). The time-to-maturity is also known as tenor in finance- speak: 1.1 Limit of the Price of a Zero Coupon Bond ZK()1 YTT $100 1 . 06 lim Z 0 T $100 Z =$100 × 1.06−T $80 $60 $40 $20 T $0 0 10 20 30 40 50 60 70 80 90 100 Exhibit 1.3 – Limit of the zero coupon bond price as a function of tenor. §2 – Derivatives The twin problems of calculating the tangent to a curve and the area delimited by a curve were solved in the late 1600s. It came as a surprise that the tangent and the area problems are interconnected. The tangent is calculated with the derivative and the area with the integral. The central idea of differential calculus is the notion of derivative. The derivative of a real- valued function y fx() in correspondence of a given value of ()x is a number that measures the slope of the function at that point. Thus, a straight line through this point, with a slope equal to the derivative, will be a tangent to the functiony fx(). More generally, the derivative of a function (often indicated as the primitive) is another function that gives the slope of fx() for each value of ()x on the domain of the function. Derivatives can be denoted in many different ways. 2.1 Notation for Derivatives dy d fx() f '() x y ' dx dx Exhibit 2.1 visualizes the derivative and tangent of the price of a zero coupon bond as a function of yield (for K = $100, T = 30, and Y = 4%). The derivative of bond prices as a function of yield is widely used in fixed-income and is the foundation of duration and convexity © G.S. Questa, 2016 TN 2 – Basic Calculus with Finance [2016-09-03] Page 4 of 16 analysis. We have chosen a long-maturity zero coupon bond (30 years) to make convexity clearly visible. $100 Z =$100 × 1.06−30 $80 $60 $40 $20 $0 0% 2% 4% 6% 8% 10% 12% Exhibit 2.1 – Derivative and tangent to the price of a zero coupon bond as a function of spot yield (at Y = 4%) Derivative and Limit The formula for calculating a derivative relies on the concept of limit and is both rigorous and intuitively obvious. 2.2 Derivative and Limit d fx( h ) fx () y' fx ( ) lim dx h0 h There are two properties to keep in mind because they play a role in understanding a number of economic and financial applications: Adding a constant (a) to a function will just shift the function upwards or downwards, while leaving its slope (derivative) unaltered Multiplying the independent variable by a constant (b) multiplies its derivative by (b) We can show how this works by using the quadratic function: 2.3 Derivative of a Quadratic Function d b() x h22 bx bx 2 lim dx h0 h bx2 b2 xh bh 22 bx lim h0 h b2 xh bh lim lim b22 x bh bx hh00h Differentiable Functions We should add that, to be differentiable for a given value of()x , a function must be both continuous and “smooth” (well-behaved) at that point. Two intuitive examples are provided by exhibits 2.2 and 2.3, which show that a differentiable function may well be non- differentiable in one point. It is interesting to note that there are functions which are both everywhere continuous and nowhere differentiable. One of these function is the Brownian motion, which plays a © G.S. Questa, 2016 TN 2 – Basic Calculus with Finance [2016-09-03] Page 5 of 16 central role in the theory of option pricing in finance. However, this is an advanced topic in stochastic calculus that cannot be covered in these induction lectures. 6 yx=1/ 4 2 0 -2 -4 -6 -10 -8 -6 -4 -2 0 2 4 6 8 10 Exhibit 2.2 – This is a rectangular hyperbola. It is everywhere continuous and differentiable, apart from a discontinuity (singularity) for x = 0. 10 yx=|| 8 6 4 2 0 -10 -8 -6 -4 -2 0 2 4 6 8 10 Exhibit 2.3 – This function is everywhere continuous. However it is not differentiable for x = 0 where the slopes on the left and on the right are not the same. In fact the derivative jumps from -1 to +1. Higher Order Derivatives If we take the derivative of a derivative we get what is called the second order derivative, which is usually written as: dy2 fy''( ) dx 2 The second derivative plays a relevant role in a number of applications, such as: Taylor series approximation Measuring convexity Determining maxima and minima of a function §3 – Taylor Series If we examine again exhibit 2.1 we can’t fail noticing that, over a small interval, the tangent is a good approximation to the original function. Therefore, in a small interval around a value © G.S. Questa, 2016 TN 2 – Basic Calculus with Finance [2016-09-03] Page 6 of 16 ()x0 the function can be expressed with the following equation which is a one-term Taylor series. (This underlies the duration metric in bond mathematics). 3.1 First Order Taylor Expansion fx() fx ()0 f '()( x 00 x x ) In bond mathematics we also use a two-term Taylor expansion, which uses the first and the second derivative of the function. 3.2 Second Order Taylor Expansion fx''( ) fx() fx () f '()( x x x )0 ( x x )2 0 002 0 §4 – Maxima and Minima of Functions The problem of finding the maximum or the minimum value of a function is one of the most pervasive in the sciences and in economics.
Load more

Recommended publications
  • Infinitesimal and Tangent to Polylogarithmic Complexes For
    AIMS Mathematics, 4(4): 1248–1257. DOI:10.3934/math.2019.4.1248 Received: 11 June 2019 Accepted: 11 August 2019 http://www.aimspress.com/journal/Math Published: 02 September 2019 Research article Infinitesimal and tangent to polylogarithmic complexes for higher weight Raziuddin Siddiqui* Department of Mathematical Sciences, Institute of Business Administration, Karachi, Pakistan * Correspondence: Email: [email protected]; Tel: +92-213-810-4700 Abstract: Motivic and polylogarithmic complexes have deep connections with K-theory. This article gives morphisms (different from Goncharov’s generalized maps) between |-vector spaces of Cathelineau’s infinitesimal complex for weight n. Our morphisms guarantee that the sequence of infinitesimal polylogs is a complex. We are also introducing a variant of Cathelineau’s complex with the derivation map for higher weight n and suggesting the definition of tangent group TBn(|). These tangent groups develop the tangent to Goncharov’s complex for weight n. Keywords: polylogarithm; infinitesimal complex; five term relation; tangent complex Mathematics Subject Classification: 11G55, 19D, 18G 1. Introduction The classical polylogarithms represented by Lin are one valued functions on a complex plane (see [11]). They are called generalization of natural logarithms, which can be represented by an infinite series (power series): X1 zk Li (z) = = − ln(1 − z) 1 k k=1 X1 zk Li (z) = 2 k2 k=1 : : X1 zk Li (z) = for z 2 ¼; jzj < 1 n kn k=1 The other versions of polylogarithms are Infinitesimal (see [8]) and Tangential (see [9]). We will discuss group theoretic form of infinitesimal and tangential polylogarithms in x 2.3, 2.4 and 2.5 below.
    [Show full text]
  • Topic 7 Notes 7 Taylor and Laurent Series
    Topic 7 Notes Jeremy Orloff 7 Taylor and Laurent series 7.1 Introduction We originally defined an analytic function as one where the derivative, defined as a limit of ratios, existed. We went on to prove Cauchy's theorem and Cauchy's integral formula. These revealed some deep properties of analytic functions, e.g. the existence of derivatives of all orders. Our goal in this topic is to express analytic functions as infinite power series. This will lead us to Taylor series. When a complex function has an isolated singularity at a point we will replace Taylor series by Laurent series. Not surprisingly we will derive these series from Cauchy's integral formula. Although we come to power series representations after exploring other properties of analytic functions, they will be one of our main tools in understanding and computing with analytic functions. 7.2 Geometric series Having a detailed understanding of geometric series will enable us to use Cauchy's integral formula to understand power series representations of analytic functions. We start with the definition: Definition. A finite geometric series has one of the following (all equivalent) forms. 2 3 n Sn = a(1 + r + r + r + ::: + r ) = a + ar + ar2 + ar3 + ::: + arn n X = arj j=0 n X = a rj j=0 The number r is called the ratio of the geometric series because it is the ratio of consecutive terms of the series. Theorem. The sum of a finite geometric series is given by a(1 − rn+1) S = a(1 + r + r2 + r3 + ::: + rn) = : (1) n 1 − r Proof.
    [Show full text]
  • Calculus for the Life Sciences I Lecture Notes – Limits, Continuity, and the Derivative
    Limits Continuity Derivative Calculus for the Life Sciences I Lecture Notes – Limits, Continuity, and the Derivative Joseph M. Mahaffy, [email protected] Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center San Diego State University San Diego, CA 92182-7720 http://www-rohan.sdsu.edu/∼jmahaffy Spring 2013 Lecture Notes – Limits, Continuity, and the Deriv Joseph M. Mahaffy, [email protected] — (1/24) Limits Continuity Derivative Outline 1 Limits Definition Examples of Limit 2 Continuity Examples of Continuity 3 Derivative Examples of a derivative Lecture Notes – Limits, Continuity, and the Deriv Joseph M. Mahaffy, [email protected] — (2/24) Limits Definition Continuity Examples of Limit Derivative Introduction Limits are central to Calculus Lecture Notes – Limits, Continuity, and the Deriv Joseph M. Mahaffy, [email protected] — (3/24) Limits Definition Continuity Examples of Limit Derivative Introduction Limits are central to Calculus Present definitions of limits, continuity, and derivative Lecture Notes – Limits, Continuity, and the Deriv Joseph M. Mahaffy, [email protected] — (3/24) Limits Definition Continuity Examples of Limit Derivative Introduction Limits are central to Calculus Present definitions of limits, continuity, and derivative Sketch the formal mathematics for these definitions Lecture Notes – Limits, Continuity, and the Deriv Joseph M. Mahaffy, [email protected] — (3/24) Limits Definition Continuity Examples of Limit Derivative Introduction Limits
    [Show full text]
  • Interval Notation and Linear Inequalities
    CHAPTER 1 Introductory Information and Review Section 1.7: Interval Notation and Linear Inequalities Linear Inequalities Linear Inequalities Rules for Solving Inequalities: 86 University of Houston Department of Mathematics SECTION 1.7 Interval Notation and Linear Inequalities Interval Notation: Example: Solution: MATH 1300 Fundamentals of Mathematics 87 CHAPTER 1 Introductory Information and Review Example: Solution: Example: 88 University of Houston Department of Mathematics SECTION 1.7 Interval Notation and Linear Inequalities Solution: Additional Example 1: Solution: MATH 1300 Fundamentals of Mathematics 89 CHAPTER 1 Introductory Information and Review Additional Example 2: Solution: 90 University of Houston Department of Mathematics SECTION 1.7 Interval Notation and Linear Inequalities Additional Example 3: Solution: Additional Example 4: Solution: MATH 1300 Fundamentals of Mathematics 91 CHAPTER 1 Introductory Information and Review Additional Example 5: Solution: Additional Example 6: Solution: 92 University of Houston Department of Mathematics SECTION 1.7 Interval Notation and Linear Inequalities Additional Example 7: Solution: MATH 1300 Fundamentals of Mathematics 93 Exercise Set 1.7: Interval Notation and Linear Inequalities For each of the following inequalities: Write each of the following inequalities in interval (a) Write the inequality algebraically. notation. (b) Graph the inequality on the real number line. (c) Write the inequality in interval notation. 23. 1. x is greater than 5. 2. x is less than 4. 24. 3. x is less than or equal to 3. 4. x is greater than or equal to 7. 25. 5. x is not equal to 2. 6. x is not equal to 5 . 26. 7. x is less than 1. 8.
    [Show full text]
  • Hegel on Calculus
    HISTORY OF PHILOSOPHY QUARTERLY Volume 34, Number 4, October 2017 HEGEL ON CALCULUS Ralph M. Kaufmann and Christopher Yeomans t is fair to say that Georg Wilhelm Friedrich Hegel’s philosophy of Imathematics and his interpretation of the calculus in particular have not been popular topics of conversation since the early part of the twenti- eth century. Changes in mathematics in the late nineteenth century, the new set-theoretical approach to understanding its foundations, and the rise of a sympathetic philosophical logic have all conspired to give prior philosophies of mathematics (including Hegel’s) the untimely appear- ance of naïveté. The common view was expressed by Bertrand Russell: The great [mathematicians] of the seventeenth and eighteenth cen- turies were so much impressed by the results of their new methods that they did not trouble to examine their foundations. Although their arguments were fallacious, a special Providence saw to it that their conclusions were more or less true. Hegel fastened upon the obscuri- ties in the foundations of mathematics, turned them into dialectical contradictions, and resolved them by nonsensical syntheses. .The resulting puzzles [of mathematics] were all cleared up during the nine- teenth century, not by heroic philosophical doctrines such as that of Kant or that of Hegel, but by patient attention to detail (1956, 368–69). Recently, however, interest in Hegel’s discussion of calculus has been awakened by an unlikely source: Gilles Deleuze. In particular, work by Simon Duffy and Henry Somers-Hall has demonstrated how close Deleuze and Hegel are in their treatment of the calculus as compared with most other philosophers of mathematics.
    [Show full text]
  • 1 Approximating Integrals Using Taylor Polynomials 1 1.1 Definitions
    Seunghee Ye Ma 8: Week 7 Nov 10 Week 7 Summary This week, we will learn how we can approximate integrals using Taylor series and numerical methods. Topics Page 1 Approximating Integrals using Taylor Polynomials 1 1.1 Definitions . .1 1.2 Examples . .2 1.3 Approximating Integrals . .3 2 Numerical Integration 5 1 Approximating Integrals using Taylor Polynomials 1.1 Definitions When we first defined the derivative, recall that it was supposed to be the \instantaneous rate of change" of a function f(x) at a given point c. In other words, f 0 gives us a linear approximation of f(x) near c: for small values of " 2 R, we have f(c + ") ≈ f(c) + "f 0(c) But if f(x) has higher order derivatives, why stop with a linear approximation? Taylor series take this idea of linear approximation and extends it to higher order derivatives, giving us a better approximation of f(x) near c. Definition (Taylor Polynomial and Taylor Series) Let f(x) be a Cn function i.e. f is n-times continuously differentiable. Then, the n-th order Taylor polynomial of f(x) about c is: n X f (k)(c) T (f)(x) = (x − c)k n k! k=0 The n-th order remainder of f(x) is: Rn(f)(x) = f(x) − Tn(f)(x) If f(x) is C1, then the Taylor series of f(x) about c is: 1 X f (k)(c) T (f)(x) = (x − c)k 1 k! k=0 Note that the first order Taylor polynomial of f(x) is precisely the linear approximation we wrote down in the beginning.
    [Show full text]
  • Interval Computations: Introduction, Uses, and Resources
    Interval Computations: Introduction, Uses, and Resources R. B. Kearfott Department of Mathematics University of Southwestern Louisiana U.S.L. Box 4-1010, Lafayette, LA 70504-1010 USA email: [email protected] Abstract Interval analysis is a broad field in which rigorous mathematics is as- sociated with with scientific computing. A number of researchers world- wide have produced a voluminous literature on the subject. This article introduces interval arithmetic and its interaction with established math- ematical theory. The article provides pointers to traditional literature collections, as well as electronic resources. Some successful scientific and engineering applications are listed. 1 What is Interval Arithmetic, and Why is it Considered? Interval arithmetic is an arithmetic defined on sets of intervals, rather than sets of real numbers. A form of interval arithmetic perhaps first appeared in 1924 and 1931 in [8, 104], then later in [98]. Modern development of interval arithmetic began with R. E. Moore’s dissertation [64]. Since then, thousands of research articles and numerous books have appeared on the subject. Periodic conferences, as well as special meetings, are held on the subject. There is an increasing amount of software support for interval computations, and more resources concerning interval computations are becoming available through the Internet. In this paper, boldface will denote intervals, lower case will denote scalar quantities, and upper case will denote vectors and matrices. Brackets “[ ]” will delimit intervals while parentheses “( )” will delimit vectors and matrices.· Un- derscores will denote lower bounds of· intervals and overscores will denote upper bounds of intervals. Corresponding lower case letters will denote components of vectors.
    [Show full text]
  • Anti-Chain Rule Name
    Anti-Chain Rule Name: The most fundamental rule for computing derivatives in calculus is the Chain Rule, from which all other differentiation rules are derived. In words, the Chain Rule states that, to differentiate f(g(x)), differentiate the outside function f and multiply by the derivative of the inside function g, so that d f(g(x)) = f 0(g(x)) · g0(x): dx The Chain Rule makes computation of nearly all derivatives fairly easy. It is tempting to think that there should be an Anti-Chain Rule that makes antidiffer- entiation as easy as the Chain Rule made differentiation. Such a rule would just reverse the process, so instead of differentiating f and multiplying by g0, we would antidifferentiate f and divide by g0. In symbols, Z F (g(x)) f(g(x)) dx = + C: g0(x) Unfortunately, the Anti-Chain Rule does not exist because the formula above is not Z always true. For example, consider (x2 + 1)2 dx. We can compute this integral (correctly) by expanding and applying the power rule: Z Z (x2 + 1)2 dx = x4 + 2x2 + 1 dx x5 2x3 = + + x + C 5 3 However, we could also think about our integrand above as f(g(x)) with f(x) = x2 and g(x) = x2 + 1. Then we have F (x) = x3=3 and g0(x) = 2x, so the Anti-Chain Rule would predict that Z F (g(x)) (x2 + 1)2 dx = + C g0(x) (x2 + 1)3 = + C 3 · 2x x6 + 3x4 + 3x2 + 1 = + C 6x x5 x3 x 1 = + + + + C 6 2 2 6x Since these answers are different, we conclude that the Anti-Chain Rule has failed us.
    [Show full text]
  • 2. the Tangent Line
    2. The Tangent Line The tangent line to a circle at a point P on its circumference is the line perpendicular to the radius of the circle at P. In Figure 1, The line T is the tangent line which is Tangent Line perpendicular to the radius of the circle at the point P. T Figure 1: A Tangent Line to a Circle While the tangent line to a circle has the property that it is perpendicular to the radius at the point of tangency, it is not this property which generalizes to other curves. We shall make an observation about the tangent line to the circle which is carried over to other curves, and may be used as its defining property. Let us look at a specific example. Let the equation of the circle in Figure 1 be x22 + y = 25. We may easily determine the equation of the tangent line to this circle at the point P(3,4). First, we observe that the radius is a segment of the line passing through the origin (0, 0) and P(3,4), and its equation is (why?). Since the tangent line is perpendicular to this line, its slope is -3/4 and passes through P(3, 4), using the point-slope formula, its equation is found to be Let us compute y-values on both the tangent line and the circle for x-values near the point P(3, 4). Note that near P, we can solve for the y-value on the upper half of the circle which is found to be When x = 3.01, we find the y-value on the tangent line is y = -3/4(3.01) + 25/4 = 3.9925, while the corresponding value on the circle is (Note that the tangent line lie above the circle, so its y-value was expected to be a larger.) In Table 1, we indicate other corresponding values as we vary x near P.
    [Show full text]
  • Automatic Linearity Detection
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Mathematical Institute Eprints Archive Report no. [13/04] Automatic linearity detection Asgeir Birkisson a Tobin A. Driscoll b aMathematical Institute, University of Oxford, 24-29 St Giles, Oxford, OX1 3LB, UK. [email protected]. Supported for this work by UK EPSRC Grant EP/E045847 and a Sloane Robinson Foundation Graduate Award associated with Lincoln College, Oxford. bDepartment of Mathematical Sciences, University of Delaware, Newark, DE 19716, USA. [email protected]. Supported for this work by UK EPSRC Grant EP/E045847. Given a function, or more generally an operator, the question \Is it lin- ear?" seems simple to answer. In many applications of scientific computing it might be worth determining the answer to this question in an automated way; some functionality, such as operator exponentiation, is only defined for linear operators, and in other problems, time saving is available if it is known that the problem being solved is linear. Linearity detection is closely connected to sparsity detection of Hessians, so for large-scale applications, memory savings can be made if linearity information is known. However, implementing such an automated detection is not as straightforward as one might expect. This paper describes how automatic linearity detection can be implemented in combination with automatic differentiation, both for stan- dard scientific computing software, and within the Chebfun software system. The key ingredients for the method are the observation that linear operators have constant derivatives, and the propagation of two logical vectors, ` and c, as computations are carried out.
    [Show full text]
  • Limits and Derivatives 2
    57425_02_ch02_p089-099.qk 11/21/08 10:34 AM Page 89 FPO thomasmayerarchive.com Limits and Derivatives 2 In A Preview of Calculus (page 3) we saw how the idea of a limit underlies the various branches of calculus. Thus it is appropriate to begin our study of calculus by investigating limits and their properties. The special type of limit that is used to find tangents and velocities gives rise to the central idea in differential calcu- lus, the derivative. We see how derivatives can be interpreted as rates of change in various situations and learn how the derivative of a function gives information about the original function. 89 57425_02_ch02_p089-099.qk 11/21/08 10:35 AM Page 90 90 CHAPTER 2 LIMITS AND DERIVATIVES 2.1 The Tangent and Velocity Problems In this section we see how limits arise when we attempt to find the tangent to a curve or the velocity of an object. The Tangent Problem The word tangent is derived from the Latin word tangens, which means “touching.” Thus t a tangent to a curve is a line that touches the curve. In other words, a tangent line should have the same direction as the curve at the point of contact. How can this idea be made precise? For a circle we could simply follow Euclid and say that a tangent is a line that intersects the circle once and only once, as in Figure 1(a). For more complicated curves this defini- tion is inadequate. Figure l(b) shows two lines and tl passing through a point P on a curve (a) C.
    [Show full text]
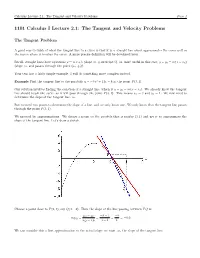
  • 1101 Calculus I Lecture 2.1: the Tangent and Velocity Problems
    Calculus Lecture 2.1: The Tangent and Velocity Problems Page 1 1101 Calculus I Lecture 2.1: The Tangent and Velocity Problems The Tangent Problem A good way to think of what the tangent line to a curve is that it is a straight line which approximates the curve well in the region where it touches the curve. A more precise definition will be developed later. Recall, straight lines have equations y = mx + b (slope m, y-intercept b), or, more useful in this case, y − y0 = m(x − x0) (slope m, and passes through the point (x0, y0)). Your text has a fairly simple example. I will do something more complex instead. Example Find the tangent line to the parabola y = −3x2 + 12x − 8 at the point P (3, 1). Our solution involves finding the equation of a straight line, which is y − y0 = m(x − x0). We already know the tangent line should touch the curve, so it will pass through the point P (3, 1). This means x0 = 3 and y0 = 1. We now need to determine the slope of the tangent line, m. But we need two points to determine the slope of a line, and we only know one. We only know that the tangent line passes through the point P (3, 1). We proceed by approximations. We choose a point on the parabola that is nearby (3,1) and use it to approximate the slope of the tangent line. Let’s draw a sketch. Choose a point close to P (3, 1), say Q(4, −8).
    [Show full text]