DOCSLIB.ORG

Fast Library for Number Theory

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Fast Library for Number Theory FLINT Fast Library for Number Theory Version 2.2.0 4 June 2011 William Hart∗, Fredrik Johanssony, Sebastian Pancratzz ∗ Supported by EPSRC Grant EP/G004870/1 y Supported by Austrian Science Foundation (FWF) Grant Y464-N18 z Supported by European Research Council Grant 204083 Contents 1 Introduction1 2 Building and using FLINT3 3 Test code5 4 Reporting bugs7 5 Contributors9 6 Example programs 11 7 FLINT macros 13 8 fmpz 15 8.1 Introduction.................................. 15 8.2 Simple example................................ 16 8.3 Memory management ............................ 16 8.4 Random generation.............................. 16 8.5 Conversion .................................. 17 8.6 Input and output............................... 18 8.7 Basic properties and manipulation ..................... 19 8.8 Comparison.................................. 19 8.9 Basic arithmetic ............................... 20 8.10 Greatest common divisor .......................... 23 8.11 Modular arithmetic.............................. 23 8.12 Bit packing and unpacking ......................... 23 8.13 Chinese remaindering ............................ 24 9 fmpz vec 27 9.1 Memory management ............................ 27 9.2 Randomisation ................................ 27 9.3 Bit sizes.................................... 27 9.4 Input and output............................... 27 9.5 Conversions.................................. 28 9.6 Assignment and basic manipulation .................... 28 9.7 Comparison.................................. 29 9.8 Sorting..................................... 29 9.9 Addition and subtraction .......................... 29 9.10 Scalar multiplication and division...................... 29 9.11 Gaussian content............................... 31 10 fmpz mat 33 10.1 Introduction.................................. 33 10.2 Simple example................................ 33 Contents iii 10.3 Memory management ............................ 34 10.4 Random matrix generation ......................... 34 10.5 Basic assignment and manipulation..................... 36 10.6 Input and output............................... 36 10.7 Comparison.................................. 37 10.8 Transpose................................... 37 10.9 Modular reduction and reconstruction ................... 37 10.10 Addition and subtraction .......................... 38 10.11 Matrix-scalar arithmetic........................... 38 10.12 Matrix multiplication ............................ 39 10.13 Inverse..................................... 40 10.14 Determinant ................................. 40 10.15 Rank...................................... 40 10.16 Nonsingular solving ............................. 41 10.17 Kernel..................................... 42 10.18 Echelon form ................................. 42 10.19 Internal functions for row reduction .................... 42 11 fmpz poly 45 11.1 Introduction.................................. 45 11.2 Simple example................................ 45 11.3 Definition of the fmpz poly t type ..................... 46 11.4 Memory management ............................ 46 11.5 Polynomial parameters............................ 47 11.6 Assignment and basic manipulation .................... 47 11.7 Randomisation ................................ 49 11.8 Getting and setting coefficients....................... 49 11.9 Comparison.................................. 50 11.10 Addition and subtraction .......................... 50 11.11 Scalar multiplication and division...................... 51 11.12 Bit packing.................................. 52 11.13 Multiplication................................. 53 11.14 Powering ................................... 55 11.15 Shifting .................................... 57 11.16 Norms..................................... 57 11.17 Greatest common divisor .......................... 58 11.18 Gaussian content............................... 60 11.19 Euclidean division .............................. 60 11.20 Divisibility testing .............................. 64 11.21 Power series division............................. 64 11.22 Pseudo division................................ 65 11.23 Derivative................................... 67 11.24 Evaluation................................... 67 11.25 Interpolation ................................. 68 11.26 Composition ................................. 68 11.27 Signature ................................... 69 11.28 Input and output............................... 70 11.29 Modular reduction and reconstruction ................... 72 11.30 Products.................................... 73 12 fmpq 75 12.1 Introduction.................................. 75 12.2 Memory management ............................ 75 12.3 Canonicalisation ............................... 75 iv Contents 12.4 Basic assignment............................... 76 12.5 Comparison.................................. 76 12.6 Conversion .................................. 77 12.7 Input and output............................... 77 12.8 Random number generation......................... 77 12.9 Arithmetic .................................. 78 12.10 Modular reduction and rational reconstruction .............. 79 12.11 Rational enumeration ............................ 79 13 fmpq mat 81 13.1 Introduction.................................. 81 13.2 Memory management ............................ 81 13.3 Entry access.................................. 81 13.4 Basic assignment............................... 82 13.5 Addition, scalar multiplication ....................... 82 13.6 Input and output............................... 82 13.7 Random matrix generation ......................... 83 13.8 Special matrices ............................... 83 13.9 Basic comparison and properties ...................... 83 13.10 Integer matrix conversion .......................... 83 13.11 Modular reduction and rational reconstruction .............. 84 13.12 Matrix multiplication ............................ 84 13.13 Determinant ................................. 85 13.14 Nonsingular solving ............................. 85 13.15 Inverse..................................... 85 13.16 Echelon form ................................. 86 14 fmpq poly 87 14.1 Introduction.................................. 87 14.2 Memory management ............................ 87 14.3 Polynomial parameters............................ 89 14.4 Accessing the numerator and denominator................. 89 14.5 Random testing................................ 89 14.6 Assignment, swap, negation......................... 90 14.7 Setting and getting coefficients ....................... 91 14.8 Comparison.................................. 92 14.9 Addition and subtraction .......................... 92 14.10 Scalar multiplication and division...................... 93 14.11 Multiplication................................. 95 14.12 Powering ................................... 96 14.13 Shifting .................................... 96 14.14 Euclidean division .............................. 96 14.15 Power series division............................. 97 14.16 Derivative and integral............................ 98 14.17 Square roots ................................. 98 14.18 Transcendental functions........................... 98 14.19 Evaluation...................................101 14.20 Interpolation .................................101 14.21 Composition .................................102 14.22 Gaussian content...............................102 14.23 Square-free ..................................103 14.24 Input and output...............................103 15 fmpz poly q 105 Contents v 15.1 Introduction..................................105 15.2 Simple example................................105 15.3 Memory management ............................106 15.4 Randomisation ................................106 15.5 Assignment..................................107 15.6 Comparison..................................107 15.7 Addition and subtraction ..........................107 15.8 Scalar multiplication and division......................108 15.9 Multiplication and division .........................108 15.10 Powering ...................................109 15.11 Derivative...................................109 15.12 Evaluation...................................109 15.13 Input and output...............................109 16 fmpz poly mat 111 16.1 Simple example................................111 16.2 Memory management ............................112 16.3 Basic assignment and manipulation.....................112 16.4 Input and output...............................112 16.5 Random matrix generation .........................112 16.6 Special matrices ...............................112 16.7 Basic comparison and properties ......................113 16.8 Norms.....................................113 16.9 Evaluation...................................113 16.10 Arithmetic ..................................113 16.11 Row reduction ................................114 16.12 Determinants.................................114 17 nmod vec 115 17.1 Memory management ............................115 17.2 Modular reduction and arithmetic .....................115 17.3 Random functions ..............................116 17.4 Basic manipulation and comparison ....................116 17.5 Arithmetic operations ............................117 18 nmod poly 119 18.1 Introduction..................................119 18.2 Simple example................................119 18.3 Definition of the nmod poly t type.....................120
Load more

Recommended publications
  • Version 0.5.1 of 5 March 2010
    Modern Computer Arithmetic Richard P. Brent and Paul Zimmermann Version 0.5.1 of 5 March 2010 iii Copyright c 2003-2010 Richard P. Brent and Paul Zimmermann ° This electronic version is distributed under the terms and conditions of the Creative Commons license “Attribution-Noncommercial-No Derivative Works 3.0”. You are free to copy, distribute and transmit this book under the following conditions: Attribution. You must attribute the work in the manner specified by the • author or licensor (but not in any way that suggests that they endorse you or your use of the work). Noncommercial. You may not use this work for commercial purposes. • No Derivative Works. You may not alter, transform, or build upon this • work. For any reuse or distribution, you must make clear to others the license terms of this work. The best way to do this is with a link to the web page below. Any of the above conditions can be waived if you get permission from the copyright holder. Nothing in this license impairs or restricts the author’s moral rights. For more information about the license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/ Contents Preface page ix Acknowledgements xi Notation xiii 1 Integer Arithmetic 1 1.1 Representation and Notations 1 1.2 Addition and Subtraction 2 1.3 Multiplication 3 1.3.1 Naive Multiplication 4 1.3.2 Karatsuba’s Algorithm 5 1.3.3 Toom-Cook Multiplication 6 1.3.4 Use of the Fast Fourier Transform (FFT) 8 1.3.5 Unbalanced Multiplication 8 1.3.6 Squaring 11 1.3.7 Multiplication by a Constant 13 1.4 Division 14 1.4.1 Naive
    [Show full text]
  • Fast Integer Division – a Differentiated Offering from C2000 Product Family
    Application Report SPRACN6–July 2019 Fast Integer Division – A Differentiated Offering From C2000™ Product Family Prasanth Viswanathan Pillai, Himanshu Chaudhary, Aravindhan Karuppiah, Alex Tessarolo ABSTRACT This application report provides an overview of the different division and modulo (remainder) functions and its associated properties. Later, the document describes how the different division functions can be implemented using the C28x ISA and intrinsics supported by the compiler. Contents 1 Introduction ................................................................................................................... 2 2 Different Division Functions ................................................................................................ 2 3 Intrinsic Support Through TI C2000 Compiler ........................................................................... 4 4 Cycle Count................................................................................................................... 6 5 Summary...................................................................................................................... 6 6 References ................................................................................................................... 6 List of Figures 1 Truncated Division Function................................................................................................ 2 2 Floored Division Function................................................................................................... 3 3 Euclidean
    [Show full text]
  • Dividing Whole Numbers
    Dividing Whole Numbers INTRODUCTION Consider the following situations: 1. Edgar brought home 72 donut holes for the 9 children at his daughter’s slumber party. How many will each child receive if the donut holes are divided equally among all nine? 2. Three friends, Gloria, Jan, and Mie-Yun won a small lottery prize of $1,450. If they split it equally among all three, how much will each get? 3. Shawntee just purchased a used car. She has agreed to pay a total of $6,200 over a 36- month period. What will her monthly payments be? 4. 195 people are planning to attend an awards banquet. Ruben is in charge of the table rental. If each table seats 8, how many tables are needed so that everyone has a seat? Each of these problems can be answered using division. As you’ll recall from Section 1.2, the result of division is called the quotient. Here are the parts of a division problem: Standard form: dividend ÷ divisor = quotient Long division form: dividend Fraction form: divisor = quotient We use these words—dividend, divisor, and quotient—throughout this section, so it’s important that you become familiar with them. You’ll often see this little diagram as a continual reminder of their proper placement. Here is how a division problem is read: In the standard form: 15 ÷ 5 is read “15 divided by 5.” In the long division form: 5 15 is read “5 divided into 15.” 15 In the fraction form: 5 is read “15 divided by 5.” Dividing Whole Numbers page 1 Example 1: In this division problem, identify the dividend, divisor, and quotient.
    [Show full text]
  • Anthyphairesis, the ``Originary'' Core of the Concept of Fraction
    Anthyphairesis, the “originary” core of the concept of fraction Paolo Longoni, Gianstefano Riva, Ernesto Rottoli To cite this version: Paolo Longoni, Gianstefano Riva, Ernesto Rottoli. Anthyphairesis, the “originary” core of the concept of fraction. History and Pedagogy of Mathematics, Jul 2016, Montpellier, France. hal-01349271 HAL Id: hal-01349271 https://hal.archives-ouvertes.fr/hal-01349271 Submitted on 27 Jul 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. ANTHYPHAIRESIS, THE “ORIGINARY” CORE OF THE CONCEPT OF FRACTION Paolo LONGONI, Gianstefano RIVA, Ernesto ROTTOLI Laboratorio didattico di matematica e filosofia. Presezzo, Bergamo, Italy [email protected] ABSTRACT In spite of efforts over decades, the results of teaching and learning fractions are not satisfactory. In response to this trouble, we have proposed a radical rethinking of the didactics of fractions, that begins with the third grade of primary school. In this presentation, we propose some historical reflections that underline the “originary” meaning of the concept of fraction. Our starting point is to retrace the anthyphairesis, in order to feel, at least partially, the “originary sensibility” that characterized the Pythagorean search. The walking step by step the concrete actions of this procedure of comparison of two homogeneous quantities, results in proposing that a process of mathematisation is the core of didactics of fractions.
    [Show full text]
  • Introduction to Abstract Algebra “Rings First”
    Introduction to Abstract Algebra \Rings First" Bruno Benedetti University of Miami January 2020 Abstract The main purpose of these notes is to understand what Z; Q; R; C are, as well as their polynomial rings. Contents 0 Preliminaries 4 0.1 Injective and Surjective Functions..........................4 0.2 Natural numbers, induction, and Euclid's theorem.................6 0.3 The Euclidean Algorithm and Diophantine Equations............... 12 0.4 From Z and Q to R: The need for geometry..................... 18 0.5 Modular Arithmetics and Divisibility Criteria.................... 23 0.6 *Fermat's little theorem and decimal representation................ 28 0.7 Exercises........................................ 31 1 C-Rings, Fields and Domains 33 1.1 Invertible elements and Fields............................. 34 1.2 Zerodivisors and Domains............................... 36 1.3 Nilpotent elements and reduced C-rings....................... 39 1.4 *Gaussian Integers................................... 39 1.5 Exercises........................................ 41 2 Polynomials 43 2.1 Degree of a polynomial................................. 44 2.2 Euclidean division................................... 46 2.3 Complex conjugation.................................. 50 2.4 Symmetric Polynomials................................ 52 2.5 Exercises........................................ 56 3 Subrings, Homomorphisms, Ideals 57 3.1 Subrings......................................... 57 3.2 Homomorphisms.................................... 58 3.3 Ideals.........................................
    [Show full text]
  • A Binary Recursive Gcd Algorithm
    A Binary Recursive Gcd Algorithm Damien Stehle´ and Paul Zimmermann LORIA/INRIA Lorraine, 615 rue du jardin botanique, BP 101, F-54602 Villers-l`es-Nancy, France, fstehle,[email protected] Abstract. The binary algorithm is a variant of the Euclidean algorithm that performs well in practice. We present a quasi-linear time recursive algorithm that computes the greatest common divisor of two integers by simulating a slightly modified version of the binary algorithm. The structure of our algorithm is very close to the one of the well-known Knuth-Sch¨onhage fast gcd algorithm; although it does not improve on its O(M(n) log n) complexity, the description and the proof of correctness are significantly simpler in our case. This leads to a simplification of the implementation and to better running times. 1 Introduction Gcd computation is a central task in computer algebra, in particular when com- puting over rational numbers or over modular integers. The well-known Eu- clidean algorithm solves this problem in time quadratic in the size n of the inputs. This algorithm has been extensively studied and analyzed over the past decades. We refer to the very complete average complexity analysis of Vall´ee for a large family of gcd algorithms, see [10]. The first quasi-linear algorithm for the integer gcd was proposed by Knuth in 1970, see [4]: he showed how to calculate the gcd of two n-bit integers in time O(n log5 n log log n). The complexity of this algorithm was improved by Sch¨onhage [6] to O(n log2 n log log n).
    [Show full text]
  • Numerical Stability of Euclidean Algorithm Over Ultrametric Fields
    Xavier CARUSO Numerical stability of Euclidean algorithm over ultrametric fields Tome 29, no 2 (2017), p. 503-534. <http://jtnb.cedram.org/item?id=JTNB_2017__29_2_503_0> © Société Arithmétique de Bordeaux, 2017, tous droits réservés. L’accès aux articles de la revue « Journal de Théorie des Nom- bres de Bordeaux » (http://jtnb.cedram.org/), implique l’accord avec les conditions générales d’utilisation (http://jtnb.cedram. org/legal/). Toute reproduction en tout ou partie de cet article sous quelque forme que ce soit pour tout usage autre que l’utilisation à fin strictement personnelle du copiste est constitutive d’une infrac- tion pénale. Toute copie ou impression de ce fichier doit contenir la présente mention de copyright. cedram Article mis en ligne dans le cadre du Centre de diffusion des revues académiques de mathématiques http://www.cedram.org/ Journal de Théorie des Nombres de Bordeaux 29 (2017), 503–534 Numerical stability of Euclidean algorithm over ultrametric fields par Xavier CARUSO Résumé. Nous étudions le problème de la stabilité du calcul des résultants et sous-résultants des polynômes définis sur des an- neaux de valuation discrète complets (e.g. Zp ou k[[t]] où k est un corps). Nous démontrons que les algorithmes de type Euclide sont très instables en moyenne et, dans de nombreux cas, nous ex- pliquons comment les rendre stables sans dégrader la complexité. Chemin faisant, nous déterminons la loi de la valuation des sous- résultants de deux polynômes p-adiques aléatoires unitaires de même degré. Abstract. We address the problem of the stability of the com- putations of resultants and subresultants of polynomials defined over complete discrete valuation rings (e.g.
    [Show full text]
  • Modern Computer Arithmetic
    Modern Computer Arithmetic Richard P. Brent and Paul Zimmermann Version 0.3 Copyright c 2003-2009 Richard P. Brent and Paul Zimmermann This electronic version is distributed under the terms and conditions of the Creative Commons license “Attribution-Noncommercial-No Derivative Works 3.0”. You are free to copy, distribute and transmit this book under the following conditions: Attribution. You must attribute the work in the manner specified • by the author or licensor (but not in any way that suggests that they endorse you or your use of the work). Noncommercial. You may not use this work for commercial purposes. • No Derivative Works. You may not alter, transform, or build upon • this work. For any reuse or distribution, you must make clear to others the license terms of this work. The best way to do this is with a link to the web page below. Any of the above conditions can be waived if you get permission from the copyright holder. Nothing in this license impairs or restricts the author’s moral rights. For more information about the license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/ Preface This is a book about algorithms for performing arithmetic, and their imple- mentation on modern computers. We are concerned with software more than hardware — we do not cover computer architecture or the design of computer hardware since good books are already available on these topics. Instead we focus on algorithms for efficiently performing arithmetic operations such as addition, multiplication and division, and their connections to topics such as modular arithmetic, greatest common divisors, the Fast Fourier Transform (FFT), and the computation of special functions.
    [Show full text]
  • Modern Computer Arithmetic (Version 0.5. 1)
    Modern Computer Arithmetic Richard P. Brent and Paul Zimmermann Version 0.5.1 arXiv:1004.4710v1 [cs.DS] 27 Apr 2010 Copyright c 2003-2010 Richard P. Brent and Paul Zimmermann This electronic version is distributed under the terms and conditions of the Creative Commons license “Attribution-Noncommercial-No Derivative Works 3.0”. You are free to copy, distribute and transmit this book under the following conditions: Attribution. You must attribute the work in the manner specified • by the author or licensor (but not in any way that suggests that they endorse you or your use of the work). Noncommercial. You may not use this work for commercial purposes. • No Derivative Works. You may not alter, transform, or build upon • this work. For any reuse or distribution, you must make clear to others the license terms of this work. The best way to do this is with a link to the web page below. Any of the above conditions can be waived if you get permission from the copyright holder. Nothing in this license impairs or restricts the author’s moral rights. For more information about the license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/ Contents Contents iii Preface ix Acknowledgements xi Notation xiii 1 Integer Arithmetic 1 1.1 RepresentationandNotations . 1 1.2 AdditionandSubtraction . .. 2 1.3 Multiplication . 3 1.3.1 Naive Multiplication . 4 1.3.2 Karatsuba’s Algorithm . 5 1.3.3 Toom-Cook Multiplication . 7 1.3.4 UseoftheFastFourierTransform(FFT) . 8 1.3.5 Unbalanced Multiplication . 9 1.3.6 Squaring.......................... 12 1.3.7 Multiplication by a Constant .
    [Show full text]
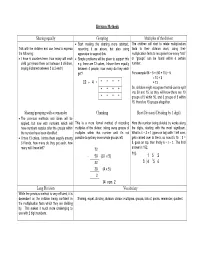
  • Division Methods Sharing Equally Grouping Multiples of the Divisor
    Division Methods Sharing equally Grouping Multiples of the divisor • Start making the sharing more abstract, The children will start to relate multiplication Talk with the children and use items to express recording it as above, but also using facts to their division work, using their the following: apparatus to support this. multiplication facts to recognise how many “lots” • I have 6 counters here, how many will each • Simple problems will be given to support this or “groups” can be found within a certain child get (share them out between 3 children, e.g. there are 12 cakes, I share them equally number. saying 6 shared between 3 is 2 each) between 4 people, how many do they each get? For example 65 ÷ 5 = (50 + 15) ÷ 5 = 10 + 3 12 ÷ 4 = * * * * = 13 So, children might recognise that 65 can be split * * * * into 50 and 15, so they will know there are 10 * * * * groups of 5 within 50, and 3 groups of 5 within 15, therefore 13 groups altogether. Sharing/grouping with a remainder Chunking Short Division (Dividing by 1 digit) • The previous methods and ideas will be applied, but now with numbers which will This is a more formal method of recording Here the number being divided by works along have numbers surplus after the groups within multiples of the divisor, taking away groups of the digits, starting with the most significant. the number have been identified. multiples within that number until it’s not What is 4 ÷ 3 = 1 (goes on top) with 1 left over, • I have 13 cakes, I share them equally among possible to get any more whole groups left.
    [Show full text]
  • Division of Whole Numbers
    The Improving Mathematics Education in Schools (TIMES) Project NUMBER AND ALGEBRA Module 10 DIVISION OF WHOLE NUMBERS A guide for teachers - Years 4–7 June 2011 4YEARS 7 Polynomials (Number and Algebra: Module 10) For teachers of Primary and Secondary Mathematics 510 Cover design, Layout design and Typesetting by Claire Ho The Improving Mathematics Education in Schools (TIMES) Project 2009‑2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations. The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations. © The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE‑EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution‑ NonCommercial‑NoDerivs 3.0 Unported License. 2011. http://creativecommons.org/licenses/by‑nc‑nd/3.0/ The Improving Mathematics Education in Schools (TIMES) Project NUMBER AND ALGEBRA Module 10 DIVISION OF WHOLE NUMBERS A guide for teachers - Years 4–7 June 2011 Peter Brown Michael Evans David Hunt Janine McIntosh Bill Pender Jacqui Ramagge 4YEARS 7 {4} A guide for teachers DIVISION OF WHOLE NUMBERS ASSUMED KNOWLEDGE • An understanding of the Hindu‑Arabic notation and place value as applied to whole numbers (see the module Using place value to write numbers). • An understanding of, and fluency with, forwards and backwards skip‑counting. • An understanding of, and fluency with, addition, subtraction and multiplication, including the use of algorithms.
    [Show full text]
  • ASSIGNMENT SUB : Mathematics CLASS : VI a WEEK – 8 …………………………………………………………………………………………………………
    ASSIGNMENT SUB : Mathematics CLASS : VI A WEEK – 8 ………………………………………………………………………………………………………… Chapter :- 03 , Factors and Multiples Topics :- (i) Highest common factor (HCF) (ii) Least common Multiples (LCM) (iii) Relation between HCF and LCM _____________________________________________________________________________________ i. Highest common factor (HCF) The Highest common factor (HCF) of two or more numbers is the largest numbers in the common factor of the numbers. HCF is also known as GCD (Greatest common Divisor) The following are the methods of finding the HCF of two or more numbers. i) Finding HCF by listing factors. ii) Prime Factorisation Method iii) Short Division Method iv) Continued or long Division Method. 1. Finding HCF by listing factors :- Consider three numbers 36, 42 and 24. Factors of 36 = 1 2 3 4 6 9 12 18 36 Factors of 42 = 1 2 3 6 7 14 21 42 Factors of 24 = 1 2 3 4 6 8 12 24 Common factors (HCF) of 36 , 42 and 24 = 1, 2, 3, 6 HCF = 6 which exactly divides the numbers 36, 42 and 24. 2. Prime factorization method :- In this method first find the prime factorization of the given numbers and then multiply the common factors to get HCF of the given numbers. Prime factors of 48 = 2 x 2 x 2 x 2 x 3 Prime factors of 96 = 2 x 2 x 2 x 2 x 3 x 2 Prime factors of 144 = 2 x 2 x 2 x 2 x 3 x 3 Common factors = 2 , 2 , 2 , 2 , 3 HCF of 48 , 96 and 144 = 2 x 2 x 2 x 2 x 3 = 48 Ans.
    [Show full text]