Microwave Antenna Holography
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Application of Metamaterials for the Microwave Antenna Realisations*
SERBIAN JOURNAL OF ELECTRICAL ENGINEERING Vol. 9, No. 1, February 2012, 1-7 UDK: 621.396.67:66.017 DOI: 10.2298/SJEE1201001A Application of Metamaterials for the Microwave Antenna Realisations* Tatjana Asenov1, Nebojša Dončov1, Bratislav Milovanović1 Abstract: In this paper, the application of left-handed metamaterials for the realisation of microwave antennas has been considered. Special emphasis is placed on lens antennas based on gradient-index metamaterials, and their advantages and enhanced features in comparison with conventional microwave antennas are highlighted. Keywords: Metamaterials, Gradient-index metamaterials, Lens antennas. 1 Introduction Artificial structures whose electromagnetic (EM) characteristics do not depend on the chemical composition but on the geometry of the structure units have sparked great interest among scientists in the first decade of the 21st century. These EM structures, known as metamaterials (MTM), exhibit highly unusual properties, such as extreme values of effective permittivity and permeability, phase and group velocity antiparallelism, etc. Metamaterials, particularly left- handed metamaterials (LH MTM) characterised by a simultaneously negative permittivity and permeability as well by a negative refractive index, have been proposed for the realisation of many different types of microwave components having advanced characteristics and small size [1, 2]. Heretofore a numerous MTM applications have been developed. They are novel full-space scanning fan/pencil-beam leaky-wave antennas, resonant antennas, conical-beam radiators, high-directivity arrays, smart multiple-input multiple-output systems, real-time spectrum analyzers, to name but a few [3]. As one of the potential LH MTM-based applications, the composite right- left handed (RH/LH) structures with graded refractive index profile (GRIN MTM) have been studied intensively both theoretically and experimentally in recent years [4 – 6]. -

A Review Paper on Microwave Transmission Using Reflector Antennas
International Journal of Scientific & Engineering Research Volume 8, Issue 10, October-2017 ISSN 2229-5518 251 A Review Paper on Microwave Transmission using Reflector Antennas Sandeep Kumar Singh [1],Sumi Kumari[2] Sr. Lecturer, Dept. of ECE, JBIT, Dehradun [1], Asst. Professor, Dept. of ECE, VGIET, Jaipur[2] [email protected][1] [email protected][2] Abstract: The conventional optimization problem of the beamed microwave energy transmission system is considered. The criterion of maximum efficiency of power intercept is parabolic function of distribution on the transmitting antenna. It is shown that under such a condition of amplitude distribution becomes more uniform than as the unconditional optimization. In this case, we can substantially increase the power radiated by the transmitting antenna losing the power intercept no more than 2%. Keywords: Parabolic Reflector Antenna, Radio Relay, Antenna Gain, Cassegrain Feed. I.INTRODUCTION limited to line of sight propagation; they cannot pass around hills or mountains as lower frequency radio waves can. Microwave radiation is generally defined as that electromagnetic radiation having wavelengths between radio waves and infrared III.ANTENNA radiation. Microwave radiation can be forced to travel in specially designed waveguides. Microwave radiation can be transmitted An antenna (or aerial) is an electrical device which converts through space or through the atmosphere in a microwave beam electric currents into radio waves, and vice versa. It is usually used from a microwave antenna and the microwave energy can be with a radio transmitter or radio receiver. In transmission, a radio collected with a microwave antenna. Microwave antennas are used transmitter applies an oscillating radio frequency electric current to for transmitting and receiving microwave radiation. -

Performance Analysis of MIMO Spatial Multiplexing Using Different Antenna Configurations and Modulation Technique in Rician Channel Hardeep Singh, Lavish Kansal
International Journal of Scientific & Engineering Research, Volume 5, Issue 6, June-2014 34 ISSN 2229-5518 Performance Analysis of MIMO Spatial Multiplexing using different Antenna Configurations and Modulation Technique in Rician Channel Hardeep Singh, Lavish Kansal Abstract— MIMO systems which employs multiple antennas at the transmitter as well as at the receiver side is the key technique to be employed in next generation wireless communication systems. MIMO systems provide various benefits such as Spatial Diversity, Spatial Multiplexing to improve the system performance. In this paper the MIMO SM system is analysed for different antenna configurations (2×2, 3×3, 4×4) in Rician channel. The performance of the MIMO SM system is investigated for higher order modulation schemes (M-PSK, M-QAM) and Zero Forcing equalizer is employed at the receiving side. The simulation results points that if antenna configurations are shifted from 2×2 to 3×3 configuration, an improvement of 0 to 2.9 db in SNR is being noted and an improvement of 0 to 2.9 db is visualized if antenna configurations are changed from 3×3 to 4×4 configuration. Index Terms— Multiple Input Multiple Output (MIMO), Zero Forcing (ZF), Spatial Multiplexing (SM), M-ary Phase Shift Keying (M-PSK) M-ary Quadrature Amplitude Modulation (M-QAM), Bit Error Rate (BER), Signal to Noise Ratio (SNR). —————————— —————————— 1 INTRODUCTION IMO (Multiple Input Multiple Output) systems employ higher extend, but the benefits of beamforming technique are multiple antennas at both the ends of a communication limited in such environments. Mlink. The MIMO systems provide various applications In order to obtain channel state information at receiving side, such as beamforming (increasing the average SNR at receiver the pilot bits are sent along with the transmitted sequence to side), Spatial Diversity (to achieve good BER at low SNR), Spa- estimate the channel state. -
Analysis of Dual-Channel Broadcast Antennas
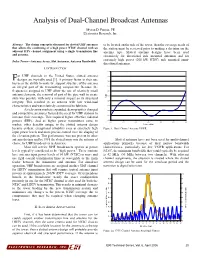
Analysis of Dual-Channel Broadcast Antennas Myron D. Fanton, PE Electronics Research, Inc. Abstract—The design concept is discussed for slotted UHF antennas to be located on the side of the tower, then the coverage needs of that allows the combining of a high power NTSC channel with an the station must be reviewed prior to making a decision on the adjacent DTV channel assignment using a single transmission line antenna type. Slotted antenna designs have been used and antenna. extensively for directional side mounted antennas and for extremely high power (200 kW NTSC) side mounted omni- Index Terms—Antenna Array, Slot Antennas, Antenna Bandwidth. directional antennas. I. INTRODUCTION 1.10 or UHF channels in the United States, slotted antenna 1.09 designs are typically used [1]. A primary factor in their use F 1.08 has been the ability to make the support structure of the antenna an integral part of the transmitting components. Because the 1.07 frequencies assigned to UHF allow the use of relatively small 1.06 antenna elements, the removal of part of the pipe wall to create 1.05 slots was possible with only a minimal impact an its structural VSWR integrity. This resulted in an antenna with low wind-load 1.04 characteristics and was relatively economical to fabricate. 1.03 As television markets expanded, demographics changed 1.02 and competitive pressures fostered the need for UHF stations to increase their coverage. This required higher effective radiated 1.01 1.00 powers (ERP). And as higher power transmitters came to 572 574 576 578 580 582 584 market, other benefits unique to the slotted antenna design Frequency (MHz) became evident: exceptional reliability even at extremely high Figure 1: Dual Channel Antenna VSWR input power levels and more precise control over the shaping of the elevation pattern. -

Importance of Microwave Antenna in Communication System
ISSN (Print) : 2320 – 3765 ISSN (Online): 2278 – 8875 International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering (A High Impact Factor, Monthly, Peer Reviewed Journal) Website: www.ijareeie.com Vol. 7, Issue 2, February 2018 Importance of Microwave Antenna in Communication System Shailesh Patwa1, Shubham Yadav2, Mohammad Saqib3 UG Student [BE], Dept. of ECE, Medicaps Institute of Technology and Management College, Indore, Madhya Pradesh, India1 UG Student [BE], Dept. of ECE, Medicaps Institute of Technology and Management College, Indore, Madhya Pradesh, India2 UG Student [BE], Dept. of ECE, Medicaps Institute of Technology and Management College, Indore, Madhya Pradesh, India3 ABSTRACT: This paper provide various types of information about microwave antenna in communication system. Antenna plays a crucial role in this communication system, which is used to transmit and receive the data. The classification of the antenna is based on the specifications like frequency, polarization, radiation, etc. In this we will observe some important point about microwave antenna in communication network, relay stations, transmission system, interconnection cable and inter-operations performing as an integrated whole. KEYWORDS: Microwave Antenna, Types of Antenna, Properties of Antenna, Applications of Antenna. I. INTRODUCTION The main purpose of this research to help people know many things about microwave antenna use in communication system. Microwaves are widely used for point-to-point communications because their small wavelength allows conveniently-sized antennas to direct them in narrow beams, which can be pointed directly at the receiving antenna. This allows nearby microwave equipment to use the same frequencies without interfering with each other, as lower frequency radio waves do. -

Microwave Antenna Performance Metrics
Chapter 5 Microwave Antenna Performance Metrics Paul Osaretin Otasowie Additional information is available at the end of the chapter http://dx.doi.org/10.5772/48517 1. Introduction An antenna is a conductor or group of conductors used for radiating electromagnetic energy into space or collecting electromagnetic energy from space. When radio frequency signal has been generated in a transmitter, some means must be used to radiate this signal through space to a receiver. The device that does this job is the antenna. The transmitter signal energy is sent into space by a transmitting antenna and the radio frequency energy is then picked up from space by a receiving antenna. The radio frequency energy that is transmitted into space is in the form of an electromagnetic field. As the electromagnetic field arrives at the receiving antenna, a voltage is induced into the antenna. The radio frequency voltage induced into the receiving antenna is then passed into the receiver. There are many different types of antennas in use today but emphasis is on antennas that operate at microwave frequencies. This chapter discusses the two major types microwave antenna which are the horn-reflector and parabolic dish antennas. In order to satisfy antenna system requirements for microwave propagation and choose a suitable antenna system, microwave design engineers must evaluate properly these antenna properties in order to achieve optimum performance. 1.1. Definition of microwave and microwave transmission Microwaves refer to radio waves with wavelength ranging from as long as one meter to as short as one millimeter or equivalently with frequencies between 300MHZ (0.3GHZ) and 300GHZ. -

Inexpensive Microwave Antenna Demonstrations Based on the IEEE Presentation by John Kraus – Jon Wallace
Inexpensive Microwave Antenna Demonstrations Based on the IEEE Presentation by John Kraus – Jon Wallace Abstract: After seeing a video of John Kraus giving a demonstration on radio antennas to the IEEE many years ago, the author was so inspired that he researched the concepts and sought to reproduce as much of the demonstration as he could. It is hoped that these demonstrations will educate and inspire others to explore as well. They cover topics which include: beam width, inverse square law, polarization, reflection, refraction, interference, absorption, gain, wave guides, diffraction, and more. The equipment used consists of a Gunn diode source with horn antenna and a WR-90 horn antenna with crystal detector, instrumentation amplifier, and voltage controlled oscillator (VCO) so that changes in intensity will be heard as pitch changes. Safety Although these microwave frequencies are not the ones used for cooking, they can still cause damage to eyes and sensitive areas of the body. When I started this project I searched for the most stringent safety recommendations I could find for a 10 mW transmitter at about 10 GHz. This recommendation was to keep a minimum distance of 60 cm. (2 ft.). I also designed an aluminum-screened mask that can be worn when presenting the demonstrations. It completely blocks all radiation from the transmitter. Close-up pictures and hints on making one are included at the end of this document. Stay safe! The Equipment The various demonstration devices will be described in each section and building tips are included at the end of the paper. The basic equipment consists of a transmitter (a Gunn diode device) with a larger horn and regulated 8V power supply powered by a 9V battery, a receiver with a small horn antenna, crystal detector, instrumentation amplifier, voltage controlled oscillator, and powerful speaker. -

Simple Antenna Can Help Kick Costly Cable TV Habit
Simple antenna can help kick costly cable TV habit By Gregory Karp, Chicago Tribune [email protected] Terrain, trees and buildings can affect signals and the type of antenna that works best at your location. (Comstock Images) As more people rethink ways to get television programming outside the traditional cable and satellite companies, the unsung TV antenna is becoming a fundamental component of their cord-cutting strategy. That makes sense. Not only are broadcast TV signals free, but even a simple antenna can produce the best picture you've ever seen on your TV because the high-definition signals are less compressed than through cable or satellite. And new flat, wall-mounted indoor antennas are a cinch to install and far less offensive aesthetically than the old rabbit ears — some can be affixed to a window behind drapes, for example. And with a one-time cost of about $50 for about 50 channels — including almost all of the most popular 50 shows — the switch is a frugal- spender's delight. HBO recently announced it would offer streaming online HBO service without a cable or satellite subscription, removing yet another reason people remain tethered to a paid-TV provider. ESPN, perhaps the largest hurdle to cutting cords, reportedly is looking into the same thing. Antenna sales spiked several years ago with the switch to digital broadcast signals, but the antenna business has continued to flourish, said Ian Geise, senior vice president of Voxx Accessories, the largest seller of TV antennas under such names as Terk and RCA. "It's really been this shift in mindset for people and (their) television entertainment," he said. -

AWS Microwave Antenna System Relocation Kit
AWS Microwave Antenna System Relocation Kit Key Products for 18 GHz Point-to-Point Applications The Clear Choice™ Radio Frequency Systems is the wireless Contact Information and broadcast infrastructure company Radio Frequency Systems with the strength and resources to serve 200 Pondview Drive the global market with a commanding Meriden, CT 06450 USA array of antenna systems and sub-system Sales & Customer Support solutions. Phone: (203) 630-3311 (800) 321-4700 (Toll-Free USA & Canada) RFS spans the continents with strategically Fax: (203) 634-2272 Email: [email protected] located operations, encompassing design, Catalog/Literature manufacturing, distribution, sales and Phone: (877) RFSWORLD service operations for markets in North Email: [email protected] America, South America, Europe, Africa, Technical Support the Middle East, Australia, Southeast Asia Phone: (203) 630-3311 x1880 (800) 659-1880 (Toll-Free USA & Canada) and China. Email: [email protected] Radio Frequency Systems brings a long tra- dition of design, engineering and manu- facturing expertise to carriers, OEMs, dis- Table of Contents tributors and systems integrators in the broadcast, cellular, land-mobile, Model Number Description Page microwave and government markets. Solid Parabolic Microwave Antennas SB2-190BB CompactLine Antenna, Single Polarized, 2 ft . .1 SU4-190AZ SlimLine Ultra High Performance Antenna, Single Polarized, 4 ft . .5 SU6-190BZ SlimLine Ultra High Performance Antenna, Single Polarized, 6 ft . .9 SUX2-190BB SlimLine Ultra High Performance Antenna, Dual Polarized, 2 ft . .13 SUX4-190AZ SlimLine Ultra High Performance Antenna, Dual Polarized, 4 ft . .17 UXA4-190AZ High Cross Polar Discrimination, Dual Polarized, 4 ft . .21 UXA6-190BZ High Cross Polar Discrimination, Dual Polarized, 6 ft . -

Satellite Communications in the New Space
IEEE COMMUNICATIONS SURVEYS & TUTORIALS (DRAFT) 1 Satellite Communications in the New Space Era: A Survey and Future Challenges Oltjon Kodheli, Eva Lagunas, Nicola Maturo, Shree Krishna Sharma, Bhavani Shankar, Jesus Fabian Mendoza Montoya, Juan Carlos Merlano Duncan, Danilo Spano, Symeon Chatzinotas, Steven Kisseleff, Jorge Querol, Lei Lei, Thang X. Vu, George Goussetis Abstract—Satellite communications (SatComs) have recently This initiative named New Space has spawned a large number entered a period of renewed interest motivated by technological of innovative broadband and earth observation missions all of advances and nurtured through private investment and ventures. which require advances in SatCom systems. The present survey aims at capturing the state of the art in SatComs, while highlighting the most promising open research The purpose of this survey is to describe in a structured topics. Firstly, the main innovation drivers are motivated, such way these technological advances and to highlight the main as new constellation types, on-board processing capabilities, non- research challenges and open issues. In this direction, Section terrestrial networks and space-based data collection/processing. II provides details on the aforementioned developments and Secondly, the most promising applications are described i.e. 5G associated requirements that have spurred SatCom innovation. integration, space communications, Earth observation, aeronauti- cal and maritime tracking and communication. Subsequently, an Subsequently, Section III presents the main applications and in-depth literature review is provided across five axes: i) system use cases which are currently the focus of SatCom research. aspects, ii) air interface, iii) medium access, iv) networking, v) The next four sections describe and classify the latest SatCom testbeds & prototyping. -

Very-High-Frequency Aerosat Airborne Terminal
REFEBENCE USE ONLY. REPORT NO. FAA-RD-77-156 VERY-HIGH-FREQUENCY AEROSAT AIRBORNE TERMINAL E. 0. Kirner D. Kuntman J. Wilson BENDIX AVIONICS DIVISION P.O. Box 9414 Fort Lauderdale FL 33310 DECEMBER 1977 FINAL REPORT OOCUMENT IS AVAILABLE TO THE U.S. PUBLIC THROUGH THE NATIONAL TECHNICAL INFORMATION SERVICE, SPRINGFIELD VIRGINIA 22161 r $■; Prepared for U.S. DEPARTMENT OF TRANSPORTATION ^ FEDERAL AVIATION ADMINISTRATION "* Systems Research and Development Service 1 * Washington DC 20591 NOTICE This document is disseminated under the sponsorship of the Department of Transportation in the interest of information exchange. The United States Govern ment assumes no liability for its contents or use thereof. NOTICE The United States Government does not endorse pro ducts or manufacturers. Trade or manufacturers' names appear herein solely because they are con sidered essential to the object of this report. Technicol Report Documentation Pogc 1, Report No. 2. Governmentml AccessionA No. 3. Recipient's Calolrig No , FAA-RD-77-156 4. Title and Subtitle 5. Report Dole December 1977 VERY-HIGH-FREQUENCY AEROSAT AIRBORNE TERMINAL 6. Performing Organization Code 8. Performing Organization Report No. 7. Author's! li.O. Kirner, D. Kuntman, and J. Wilson DOT-TSC-FAA-77-17 9. Performing Organi lotion Name and Address 10. Work Unit No. fTRAIS) Bendix Avionics Division* FA711/R8122 P.O. Box 9414 1 1. Controct or Grcnt No. Fort Lauderdale FL 33310 DOT-TSC-1121 13. Type of Report and Period Covered 12. Sponsoring Agency Nome and Address Final Report U.S. Department of Transportation April 1976-March 1977 Federal Aviation Administration Systems Research and Development Service Sponsoring Agency Code Washington DC 20591 IS. -

Antennas - Catalogue 19
ANTENNAS - CATALOGUE 19 KATHREIN Broadcast GmbH Ing.-Anton-Kathrein-Str. 1–7 83101 Rohrdorf, Germany www.kathrein-bca.com [email protected] TOTAL QUALITY MANAGEMENT INDEX FM Antennas 3 VHF Antennas 39 UHF Antennas 63 Technical Notes 81 1 FM ANTENNAS INDEX FM-03 H 5 FM-03 V 9 FM-04 13 FM-05 H 15 FM-07 19 FM-34 21 FMC-01 22 FMC-01/R 24 FMC-03 26 FMC-05 30 FMC-06 34 FMC-06/R 36 FM ANTENNAS 3 FM-03 (Horizontal polarization) FM PANEL ANTENNA FEATURES • horizontal polarization • broadband 87.5 ÷ 108 MHz • 7.5 dB gain • directional pattern • suitable as a component in various arrays on square towers • stainless steel dipoles • suitable also for vertical polarization RADIATION PATTERNS (Mid Band) ELECTRICAL DATA ANTENNA TYPE FM-03 FREQUENCY RANGE 87.5 ÷ 108 MHz IMPEDANCE 50 ohm CONNECTOR 7/8” EIA MAX POWER 5 kW VSWR ≤ 1.15 POLARIZATION Horizontal GAIN (referred to half wave dipole) 7.5 dB E-Plane ± 34° HALF POWER BEAMWIDTH H-Plane ± 30° LIGHTNING PROTECTION All Metal Parts DC Grounded MECHANICAL DATA 2200 x 2000 x 991 DIMENSIONS mm (in) (86.61 x 78.74 x 39.02) WEIGHT kg (lb) 61 (134.5) 1.40 (15.1) front WIND SURFACE m2 ( ft2) 1.01 (10.9) side WIND LOAD kN (lbf) 1.76 (396) front at 160 km/h (100 mph) 1.25 (281) side MAX WIND VELOCITY km/h (mph) 270 (167.8) Reflector (hot dip galvanized steel) Dipoles (stainless steel) MATERIALS Internal parts (silver plated brass, polished brass, deoxidized aluminium) Radome (fiberglass) ICING PROTECTION Feed point radome RADOME COLOUR Grey (standard) MOUNTING Directly on supporting mast Specifications are subject to change without prior notice FM ANTENNAS 5 FM-03 (Horizontal polarization) FM PANEL ANTENNA FEATURES • radiating systems with FM-03 panel • high power systems • omnidirectional or directional patterns • equal or unequal split ratio power distribution network FM-03/32 (8x4) GUANGZHOU, P.R.C.