DOCSLIB.ORG

Lyman Alpha Forest Michael Rauch

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lyman Alpha Forest Michael Rauch eaa.iop.org DOI: 10.1888/0333750888/2140 Lyman Alpha Forest Michael Rauch From Encyclopedia of Astronomy & Astrophysics P. Murdin © IOP Publishing Ltd 2006 ISBN: 0333750888 Institute of Physics Publishing Bristol and Philadelphia Downloaded on Thu Mar 02 23:49:43 GMT 2006 [131.215.103.76] Terms and Conditions Lyman Alpha Forest E NCYCLOPEDIA OF A STRONOMY AND A STROPHYSICS Lyman Alpha Forest Lyα forest systems in this restricted definition, but we have theoretical reasons to believe that there is a genuine The Lyman alpha forest is an absorption phenomenon seen dichotomy between intergalactic gas (represented by the in the spectra of high redshift QSOs and galaxies (figure Lyα forest), even if partly polluted by metals, and the 1). It is the only direct observational evidence we have of invariably metal-enriched higher column density systems, the existence and properties of the general INTERGALACTIC thought to be related to galaxies. MEDIUM, and, as we have reason to believe, of most of the Lyα forest absorption systems have now been baryonic matter contents of the universe. observed from REDSHIFT zero (with UV satellites) up to the On its way to us the light of a bright, distant highest redshifts at which background light sources (QSOs QSO passes through intervening intergalactic gas and and galaxies) can still be found (currently z ∼ 5–6). through gas clouds associated with foreground galaxies. Absorption by the gas modifies the spectra of the The Gunn–Peterson effect: where does the background objects and imprints a record of the gas absorption come from? α clouds’ physical and chemical states on the observed Ly forest absorption in a QSO spectrum was predicted background QSO and galaxy spectra. The whole and first detected by Gunn and Peterson (1965). The arrangement is reminiscent of a giant cosmic slide basic idea is as follows: going back in time an increasing projector, where a QSO plays the role of the light bulb, fraction of the total baryonic mass of the universe must and the intervening gas clouds are the slides, changing the be in the form of gas. The absorption cross-section of α colors of the light source by absorbing parts of the (white) the Ly line of neutral hydrogen is large enough that spectrum. even if only a small fraction of the total mass of the α The name ‘Lyman α forest’ refers to the appearance universe were in the form of H I the redshifted Ly of the optical QSO spectra, which show a forest of lines should completely absorb a part of the spectrum hundreds of sharp absorption lines, mostly from the of any background light source. The absorption should neutral hydrogen (H I) Lyman α line, superimposed on the essentially assume the shape of an absorption trough α more smoothly varying QSO continuum (figure 2). Almost in a QSO spectrum, extending blueward from the Ly all the lines in the Lyman α forest correspond to the same emission of the QSO. This particular absorption pattern is atomic transition (which at 1215.67 Å is in the ultraviolet referred to in the literature as the ‘Gunn–Peterson effect’. wavelength region). The phenomenon was first observed Gunn and Peterson did detect such a trough but the light in the optical waveband (∼ 4000–9000Å) implying that the of the QSO was not completely absorbed and there was gas clouds causing the absorption are highly redshifted by some residual light left in the spectral region in question. the Hubble expansion. The absorption systems appear The relative weakness of the absorption could mean two spread out into a ‘forest’ of lines because each line is things: (a) there is little hydrogen left in intergalactic space α redshifted by a different amount in proportion to the and by the time the Ly forest is observed most of the absorbing cloud’s distance from us. The stronger ones matter has already condensed into galaxies. Or (b) most among the absorption systems do show further spectral of the hydrogen is not in neutral form, where it can produce α signatures in addition to their Lyα line: higher-order Ly absorption, but is fully ionized. Lyman series lines begin to be detectable for absorption QSO surveys (see QUASISTELLAR OBJECTS: SURVEYS) later systems with Lyα close to saturation. Clouds with H I showed that the second possibility is more important: column densities larger than N ∼ 1017 cm−2 start showing the combined ionizing radiation output from all known a discontinuity due to continuous absorption at a rest QSOs at high redshift amounts to a UV radiation field frame wavelength 912 Å, beyond the limit of the Lyman probably strong enough to keep most of the baryonic series. These ‘Lyman limit systems’ occupy a column matter in the universe highly ionized—i.e., if the baryons density regime where a gas cloud starts shielding itself are predominantly in the form of a more or less against ionizing radiation from the outside. Clouds with homogeneously distributed gas. even higher column densities (N>1019 cm−2) exhibit This conclusion is based on the assumption that the damping wings caused by the internal finite lifetime the gas is in approximate photoionization equilibrium of the Lyα transition. The gas in these ‘damped Lyα’ with the cosmic UV background field, i.e., the rate of recombinations of electrons with protons to form neutral systems (see LYMAN ALPHA ABSORPTION: THE DAMPED SYSTEMS)is hydrogen balances the rate of ionizations from the ground almost completely self-shielded and mostly neutral. Most . − state of H I, absorption systems with N>1014 5 cm 2 also show metal n n α(T ) = n . (1) absorption lines (triply ionized carbon and silicon, and e p HI some other common elements and ionization stages). For Here is the rate of photoionizations per neutral hydrogen that reason the higher column density systems are usually atom, caused by the hydrogen-ionizing portion of the UV n n n referred to as ‘metal’ or ‘heavy element’ systems. Here background field. The quantities e, HI and p refer to the we are concerned only with the low column density gas, number densities of electrons, neutral hydrogen atoms, i.e., those absorption systems where the Lyα line is not and protons (= ionized hydrogen), respectively. saturated, which we will refer to as the Lyα forest proper. Later observations of QSOs with higher spectral There definitely is an overlap between metal systems and resolution (< a few hundred km s−1) showed that Copyright © Nature Publishing Group 2001 Brunel Road, Houndmills, Basingstoke, Hampshire, RG21 6XS, UK Registered No. 785998 and Institute of Physics Publishing 2001 Dirac House, Temple Back, Bristol, BS1 6BE, UK 1 Lyman Alpha Forest E NCYCLOPEDIA OF A STRONOMY AND A STROPHYSICS Figure 1. High resolution spectrum of the Lyα forest part of a redshift 3.63 QSO, taken with the HIRES spectrograph on the Keck 10 m telescope in Hawaii. The plot shows the flux of the QSO in arbitrary units versus the observed wavelength in units of Angstroms. The noise level can be judged from the longer wavelength wing of the broad, intrinsic Lyα emission line of the QSO (near 5650 Å). All of the ragged features are high redshift absorption lines. Most of the lines between the QSO’s Lyα and Lyβ emission lines (the humps at 5650 and 4750 Å) are due to Lyα absorption by intervening gas. The actual rate of incidence of absorbers decreases towards shorter wavelengths (lower redshifts). Nevertheless, the line density increases to the blue because higher order absorption lines from the Lyman series appear and overlap randomly with Lyα lines of systems at lower redshift. QSO’s flux I ∝ e−τ depends exponentially on the Lyα optical depth τ, which itself depends almost quadratically on the gas density (or the electron density ne; for a highly ionized gas at constant temperature). Thus small density fluctuations produce enhanced fluctuations in the optical depth. The Lyα forest absorption is observed in velocity space, and a convergent velocity field (e.g., a collapsing gas cloud) could also produce absorption ‘lines’. Caustics in velocity space may form if several gas volume elements are moving at the same velocity relative to the observer. Indeed, if Lyα clouds are produced by gravitational collapse, both overdense regions and infall should contribute to an absorption line. Spectroscopy of the Lyα line is an incredibly sensitive method to detect baryonic matter at any redshift. The photoionization cross section of neutral hydrogen is so large that an extremely tenuous gas at or below the Figure 2. Detailed section of the previous spectrum. The image mean density of the universe can be detected easily shows a number of absorption lines all corresponding to the in absorption. The method of choice for studying the α neutral hydrogen (H I) Ly 1215.67 Å transition. Lines close to Lyα forest is optical high resolution spectroscopy, with a saturation (= zero flux in the line center) have neutral hydrogen . − λ/λ > α column density typically around N ∼ 1014 2 cm 2, spectral resolution 30 000 sufficient to resolve Ly corresponding to a gas density enhanced by roughly an order of lines thermally broadened by the photoionization heating magnitude with respect to the mean density of the universe. The from the UV background. With 8 m class telescopes, a mean redshift of the stretch shown is z = 3.248. The spectral α − spectrum of a QSO suitable for further analysis of the Ly region extends over 3480 km s 1. For a flat = 1 universe this −1 forest absorption can be obtained within a few hours of corresponds to a spatial extent of approximately 9.6 h Mpc observing time.
Load more

Recommended publications
  • Group Problems #22 - Solutions
    Group Problems #22 - Solutions Friday, October 21 Problem 1 Ritz Combination Principle Show that the longest wavelength of the Balmer series and the longest two wavelengths of the Lyman series satisfy the Ritz Combination Principle. The wavelengths corresponding to transitions between two energy levels in hydrogen is given by: n2 λ = λlimit 2 2 ; (1) n − n0 where n0 = 1 for the Lyman series, n0 = 2 for the Balmer series, and λlimit = 91:1 nm for the Lyman series and λlimit = 364:5 nm for the Balmer series. Inspection of this equation shows that the longest wavelength corresponds to the transition between n = n0 and n = n0 + 1. Thus, for the Lyman series, the longest two wavelengths are λ12 and λ13. For the Balmer series, the longest wavelength is λ23. The Ritz combination principle states that certain pairs of observed frequencies from the hydrogen spectrum add together to give other observed frequencies. For this particular problem, we then have: ν12 + ν23 = ν13 =) h(ν12 + ν23) = hν13 (2) 1 1 1 =) hc + = hc (3) λ12 λ23 λ13 1 1 1 =) + = : (4) λ12 λ23 λ13 Inverting Eqn. 1 above gives: 2 2 2 1 1 n − n0 1 n0 = 2 = 1 − 2 : (5) λ λlimit n λlimit n To calculate 1/λ12 and 1/λ13, we use the Lyman series numbers and find 1/λ12 = −1 −1 3=(4 ∗ 91:1) = 0:00823 nm and 1/λ13 = 8=(9 ∗ 91:1) = 0:00976 nm . To compute 1/λ23, we use the Balmer series numbers and find 1/λ23 = 5=(9 ∗ 364:5) = 0:00152 −1 nm .
    [Show full text]
  • Observations of the Lyman Series Forest Towards the Redshift 7.1 Quasar ULAS J1120+0641 R
    A&A 601, A16 (2017) Astronomy DOI: 10.1051/0004-6361/201630258 & c ESO 2017 Astrophysics Observations of the Lyman series forest towards the redshift 7.1 quasar ULAS J1120+0641 R. Barnett1, S. J. Warren1, G. D. Becker2, D. J. Mortlock1; 3; 4, P. C. Hewett5, R. G. McMahon5; 6, C. Simpson7, and B. P. Venemans8 1 Astrophysics Group, Blackett Laboratory, Imperial College London, London SW7 2AZ, UK e-mail: [email protected] 2 Department of Physics & Astronomy, University of California, Riverside, 900 University Avenue, Riverside, CA 92521, USA 3 Department of Mathematics, Imperial College London, London SW7 2AZ, UK 4 Department of Astronomy, Stockholm University, Albanova, 10691 Stockholm, Sweden 5 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK 6 Kavli Institute for Cosmology, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK 7 Gemini Observatory, Northern Operations Center, N. A’ohoku Place, Hilo, HI 96720, USA 8 Max-Planck Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany Received 15 December 2016 / Accepted 9 February 2017 ABSTRACT We present a 30 h integration Very Large Telescope X-shooter spectrum of the Lyman series forest towards the z = 7:084 quasar ULAS J1120+0641. The only detected transmission at S=N > 5 is confined to seven narrow spikes in the Lyα forest, over the redshift range 5:858 < z < 6:122, just longward of the wavelength of the onset of the Lyβ forest. There is also a possible detection of one further unresolved spike in the Lyβ forest at z = 6:854, with S=N = 4:5.
    [Show full text]
  • Unique Astrophysics in the Lyman Ultraviolet
    Unique Astrophysics in the Lyman Ultraviolet Jason Tumlinson1, Alessandra Aloisi1, Gerard Kriss1, Kevin France2, Stephan McCandliss3, Ken Sembach1, Andrew Fox1, Todd Tripp4, Edward Jenkins5, Matthew Beasley2, Charles Danforth2, Michael Shull2, John Stocke2, Nicolas Lehner6, Christopher Howk6, Cynthia Froning2, James Green2, Cristina Oliveira1, Alex Fullerton1, Bill Blair3, Jeff Kruk7, George Sonneborn7, Steven Penton1, Bart Wakker8, Xavier Prochaska9, John Vallerga10, Paul Scowen11 Summary: There is unique and groundbreaking science to be done with a new generation of UV spectrographs that cover wavelengths in the “Lyman Ultraviolet” (LUV; 912 - 1216 Å). There is no astrophysical basis for truncating spectroscopic wavelength coverage anywhere between the atmospheric cutoff (3100 Å) and the Lyman limit (912 Å); the usual reasons this happens are all technical. The unique science available in the LUV includes critical problems in astrophysics ranging from the habitability of exoplanets to the reionization of the IGM. Crucially, the local Universe (z ≲ 0.1) is entirely closed to many key physical diagnostics without access to the LUV. These compelling scientific problems require overcoming these technical barriers so that future UV spectrographs can extend coverage to the Lyman limit at 912 Å. The bifurcated history of the Space UV: Much the course of space astrophysics can be traced to the optical properties of ozone (O3) and magnesium fluoride (MgF2). The first causes the space UV, and the second divides the “HST UV” (1150 - 3100 Å) and the “FUSE UV” (900 - 1200 Å). This short paper argues that some critical problems in astrophysics are best solved by a future generation of high-resolution UV spectrographs that observe all wavelengths between the Lyman limit and the atmospheric cutoff.
    [Show full text]
  • Arxiv:1704.03416V1 [Astro-Ph.GA] 11 Apr 2017 2
    Physics of Lyα Radiative Transfer Mark Dijkstra (Institute of Theoretical Astrophysics, University of Oslo) (Dated: April 7, 2017) Lecture notes for the 46th Saas-Fee winterschool, 13-19 March 2016, Les Diablerets, Switzerland. See http://obswww.unige.ch/Courses/saas-fee-2016/ arXiv:1704.03416v1 [astro-ph.GA] 11 Apr 2017 2 Contents 1. Preface 3 2. Introduction 3 3. The Hydrogen Atom and Introduction to Lyα Emission Mechanisms 4 3.1. Hydrogen in our Universe 4 3.2. The Hydrogen Atom: The Classical & Quantum Picture 6 3.3. Radiative Transitions in the Hydrogen Atom: Lyman, Balmer, ..., Pfund, .... Series 8 3.4. Lyα Emission Mechanisms 9 4. A Closer Look at Lyα Emission Mechanisms & Sources 10 4.1. Collisions 10 4.2. Recombination 13 5. Astrophysical Lyα Sources 14 5.1. Interstellar HII Regions 14 5.2. The Circumgalactic/Intergalactic Medium (CGM/IGM) 16 6. Step 1 Towards Understanding Lyα Radiative Transfer: Lyα Scattering Cross-section 22 6.1. Interaction of a Free Electron with Radiation: Thomson Scattering 22 6.2. Interaction of a Bound Electron with Radiation: Lorentzian Cross-section 25 6.3. Interaction of a Bound Electron with Radiation: Relation to Lyα Cross-Section 26 6.4. Voigt Profile of Lyα Cross-Section 27 7. Step 2 Towards Understanding Lyα Radiative Transfer: The Radiative Transfer Equation 29 7.1. I: Absorption Term: Lyα Cross Section 30 7.2. II: Volume Emission Term 30 7.3. III: Scattering Term 30 7.4. IV: ‘Destruction’ Term 36 7.5. Lyα Propagation through HI: Scattering as Double Diffusion Process 38 8.
    [Show full text]
  • Balmer and Rydberg Equations for Hydrogen Spectra Revisited
    1 Balmer and Rydberg Equations for Hydrogen Spectra Revisited Raji Heyrovska Institute of Biophysics, Academy of Sciences of the Czech Republic, 135 Kralovopolska, 612 65 Brno, Czech Republic. Email: [email protected] Abstract Balmer equation for the atomic spectral lines was generalized by Rydberg. Here it is shown that 1) while Bohr's theory explains the Rydberg constant in terms of the ground state energy of the hydrogen atom, quantizing the angular momentum does not explain the Rydberg equation, 2) on reformulating Rydberg's equation, the principal quantum numbers are found to correspond to integral numbers of de Broglie waves and 3) the ground state energy of hydrogen is electromagnetic like that of photons and the frequency of the emitted or absorbed light is the difference in the frequencies of the electromagnetic energy levels. Subject terms: Chemical physics, Atomic physics, Physical chemistry, Astrophysics 2 An introduction to the development of the theory of atomic spectra can be found in [1, 2]. This article is divided into several sections and starts with section 1 on Balmer's equation for the observed spectral lines of hydrogen. 1. Balmer's equation Balmer's equation [1, 2] for the observed emitted (or absorbed) wavelengths (λ) of the spectral lines of hydrogen is given by, 2 2 2 λ = h B,n1[n2 /(n2 - n 1 )] (1) 2 where n1 and n2 (> n1) are integers with n1 having a constant value, hB,n1 = n1 hB is a constant for each series and hB is a constant. For the Lyman, Balmer, Paschen, Bracket and Pfund series, n1 = 1, 2, 3, 4 and 5 respectively.
    [Show full text]
  • Spectra of Photoionized Regions 1. Introduction
    Spectra of Photoionized Regions Friday, January 21, 2011 CONTENTS: 1. Introduction 2. Recombination Processes A. Overview B. Level networks C. Free-bound continuum D. Two-photon continuum E. Collisions 3. Additional Processes A. Lyman-α emission B. Helium processes C. Resonance fluorescence 4. Diagnostics A. Temperature B. Density C. Composition D. Star formation rates 1. Introduction Our next task is to consider the emitted spectrum from an H II region. This is one of the most important subjects observationally since spectroscopy provides our principal set of diagnostics on the physics occurring in the region. This material is (mostly) covered in Chapters 4 and 5 of Osterbrock & Ferland (on which most of these notes are based). The sources of emission we will consider fall into two categories: Cooling: Infrared fine structure lines Optical forbidden lines Free-free continuum Recombination: Free-bound continuum Recombination lines Two-photon continuua 1 Generally, the forbidden lines (optical or IR) come from metals, whereas the recombination features are proportional to abundance and arise mainly from H and He. Since the cooling radiation has already been discussed, we will focus on recombination and then proceed to diagnostics. 2. Recombination Processes A. OVERVIEW We first consider the case of recombination of hydrogen at very low densities where the collision rates are small, i.e. any hydrogen atom that forms can decay radiatively before any collision. Later on we will introduce collisions between particles (electrons, protons) with excited atoms. The recombination process at low density begins with a radiative recombination, H+ + e− → H0(nl) + γ , which populates an excited state of the hydrogen atom.
    [Show full text]
  • The Hydrogen Atom and the Lyman Series Block: ______Answer Each Question in the Space Required
    Chemistry Worksheet NAME: _____________________________ The Hydrogen Atom and the Lyman series Block: _________ Answer each question in the space required. Show all work. Pay attention to significant figures and units. 1. Hydrogen is the simplest atom in the universe, thus it is the most commonly used example for delving into the quantum world. The energy levels of hydrogen can be calculated using the 2 principle quantum number, n, in the equation En = −13.6 eV (1/n ), for n = 1, 2, 3, 4 … ∞. Recall that eV stands for the energy unit called the electron volt, which relates to joules (J) by the following conversion: 1 eV = 1.602 × 10−19 J. a. What is the value of principal quantum number, n, for the ground state of hydrogen? b. Calculate the energy (in eV and in joules) for the ground state of hydrogen. c. Calculate the energy, En, for the first four excited states of the hydrogen atom. d. Is the third excited state higher or lower in energy than the ground state? Justify your answer in one or two sentences. e. The ionization energy of hydrogen is defined as the minimum energy required to excite an electron from the ground state to a state where the electron is separated from the nucleus (the proton). From your answers above, what is the ionization energy for hydrogen? Justify your answer in one or two sentences. f. How much energy would be required to ionize an entire mole of hydrogen atoms? Copyright© 2007, Alan D. Crosby, Newton South High School, Newton, MA 02459 Chemistry Worksheet NAME: _____________________________ The Hydrogen Atom and the Lyman series Block: _________ 2.
    [Show full text]
  • Atomic Structure
    1 Atomic Structure 1 2 Atomic structure 1-1 Source 1-1 The experimental arrangement for Ruther- ford's measurement of the scattering of α particles by very thin gold foils. The source of the α particles was radioactive radium, a rays encased in a lead block that protects the surroundings from radiation and confines the α particles to a beam. The gold foil used was about 6 × 10-5 cm thick. Most of the α particles passed through the gold leaf with little or no deflection, a. A few were deflected at wide angles, b, and occasionally a particle rebounded from the foil, c, and was Gold detected by a screen or counter placed on leaf Screen the same side of the foil as the source. The concept that molecules consist of atoms bonded together in definite patterns was well established by 1860. shortly thereafter, the recognition that the bonding properties of the elements are periodic led to widespread speculation concerning the internal structure of atoms themselves. The first real break- through in the formulation of atomic structural models followed the discovery, about 1900, that atoms contain electrically charged particles—negative electrons and positive protons. From charge-to-mass ratio measurements J. J. Thomson realized that most of the mass of the atom could be accounted for by the positive (proton) portion. He proposed a jellylike atom with the small, negative electrons imbedded in the relatively large proton mass. But in 1906-1909, a series of experiments directed by Ernest Rutherford, a New Zealand physicist working in Manchester, England, provided an entirely different picture of the atom.
    [Show full text]
  • Hydrogen Atom – Lyman Series Rydberg’S Formula Hydrogen 91.19Nm Energy Λ = Levels 1 1 0Ev − M2 N2
    Hydrogen atom – Lyman Series Rydberg’s formula Hydrogen 91.19nm energy λ = levels 1 1 0eV − m2 n2 Predicts λ of nàm transition: Can Rydberg’s formula tell us what ground n (n>m) state energy is? m (m=1,2,3..) -?? eV m=1 Balmer-Rydberg formula Hydrogen energy levels 91.19nm 0eV λ = 1 1 − m2 n2 Look at energy for a transition between n=infinity and m=1 1 0 ≡ 0eV hc hc ⎛ 1 1 ⎞ Einitial − E final = = ⎜ 2 − 2 ⎟ λ 91.19nm ⎝ m n ⎠ -?? eV hc − E final = E 13.6eV 91.19nm 1 = − Hydrogen energy levels A more general case: What is 0eV the energy of each level (‘m’) in hydrogen? … 0 ≡ 0eV hc hc ⎛ 1 1 ⎞ Einitial − E final = = ⎜ 2 − 2 ⎟ λ 91.19nm ⎝ m n ⎠ -?? eV hc 1 1 − E = E = −13.6eV final 91.19nm m2 m m2 Balmer/Rydberg had a mathematical formula to describe hydrogen spectrum, but no mechanism for why it worked! Why does it work? Hydrogen energy levels 410.3 486.1Balmer’s formula656.3 nm 434.0 91.19nm λ = 1 1 − m2 n2 where m=1,2,3 and where n = m+1, m+2 The Balmer/Rydberg formula correctly describes the hydrogen spectrum! Is it a good model? The Balmer/Rydberg formula is a mathematical representation of an empirical observation. It doesn’t really explain anything. How can we explain (not only calculate) the energy levels in the hydrogen atom? Next step: A semi-classical explanation of the atomic spectra (Bohr model) Rutherford shot alpha particles at atoms and he figured out that a tiny, positive, hard core is surrounded by negative charge very far away from the core.
    [Show full text]
  • The Structure of Hydrogen
    Chapter 9 The structure of hydrogen One of the many goals of the astronomical spectroscopist is to interpret the details of spectral features in order to deduce the properties of the radiating or absorbing matter. In Chapters 4 and 5, we introduced much of the for- malism connecting the atomic absorption features observed in spectra with the all–important atomic absorption coefficient, α(λ). The mathematical form of absorption coefficients are derived directly from the theoretical model of the atom. As such, it is essential to understand the internal working nature of the atom in order to deduce the physical conditions of the matter giving rise to observed spectral features. The model of the atom is simple in principle, yet highly complex in de- tail. Employing only first–order physics, we have been extremely successful at formulating the basic atomic model, including the internal energy structure, transition probabilities, and the spectra of the various atoms and ions. How- ever, first–order physics is not complete enough to precisely describe the internal energy structure of the atom nor the observed spectral features. Enter the com- plexity of higher–order physics, which are most easily discussed in terms of small corrections to the first–order model. The simplest atom is hydrogen, which comprises a single proton for the nucleus and a single orbiting electron. The complexity of the physics increases as the number of nuclear protons and orbiting electrons increases. The hydrogen atom serves to clearly illustrate the effects of higher–order corrections while avoiding the complication of multiple interacting electrons. In this chapter, we focus on the first–order physics, internal energy structure, and resulting spectrum of neutral hydrogen and hydrogen–like ions (those with a single orbiting electron).
    [Show full text]
  • First Detection of Lyman Continuum Escape from a Local Starburst Galaxy
    A&A 448, 513–524 (2006) Astronomy DOI: 10.1051/0004-6361:20053788 & c ESO 2006 Astrophysics First detection of Lyman continuum escape from a local starburst galaxy I. Observations of the luminous blue compact galaxy Haro 11 with the Far Ultraviolet Spectroscopic Explorer (FUSE) N. Bergvall1, E. Zackrisson1, B.-G. Andersson2, D. Arnberg1,J.Masegosa3, and G. Östlin4 1 Dept. of Astronomy and Space Physics, Box 515, 75120 Uppsala, Sweden e-mail: [nils.bergvall;erik.zackrisson]@astro.uu.se 2 Department of Physics and Astronomy, Johns Hopkins University, 3400 North Charles Street, Baltimore, MD 21218, USA e-mail: [email protected] 3 Instituto de Astrofisica de Andalucia, Granada, Spain e-mail: [email protected] 4 Stockholm Observatory, SCFAB, 106 91 Stockholm, Sweden e-mail: [email protected] Received 7 July 2005 / Accepted 2 November 2005 ABSTRACT Context. The dominating reionization source in the young universe has not yet been identified. Possible candidates include metal poor dwarf galaxies with starburst properties. Aims. We selected an extreme starburst dwarf, the Blue Compact Galaxy Haro 11, with the aim of determining the Lyman continuum escape fraction from UV spectroscopy. Methods. Spectra of Haro 11 were obtained with the Far Ultraviolet Spectroscopic Explorer (FUSE). A weak signal shortwards of the Lyman break is identified as Lyman continuum (LyC) emission escaping from the ongoing starburst. From profile fitting to weak metal lines we derive column densities of the low ionization species. Adopting a metallicity typical of the H II regions of Haro 11, these data correspond to a hydrogen column density of ∼1019cm−2.
    [Show full text]
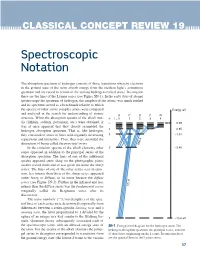
  • Spectroscopic Notation
    CLASSICAL CONCEPT REVIEW 19 Spectroscopic Notation The absorption spectrum of hydrogen consists of those transitions whereby electrons in the ground state of the atom absorb energy from the incident light’s continuous spectrum and are raised to certain of the various hydrogen excited states. In emission these are the lines of the Lyman series (see Figure SN-1). In the early days of atomic spectroscopy the spectrum of hydrogen, the simplest of the atoms, was much studied and its spectrum served as a benchmark relative to which the spectra of other, more complex atoms were compared Energy, eV and analyzed in the search for understanding of atomic S P D F G structure. When the absorption spectra of the alkali met- n l = 0 1 2 3 4 als (lithium, sodium, potassium, etc.) were obtained, it ∞ 0.00 was at once apparent that they closely resembled the hydrogen absorption spectrum. That is, like hydrogen, 4 –0.85 they consisted of series of lines with regularly decreasing 3 –1.51 separations and intensities. Thus, they were accorded the distinction of being called the principal series. 656.3 In the emission spectra of the alkali elements other 2 –3.40 series appeared in addition to the principal series of the absorption spectrum. The lines of one of the additional spectra appeared quite sharp on the photographic plates used to record them and so was given the name the sharp series. The lines of one of the other series seen in emis- sion, less intense than those of the sharp series, appeared rather fuzzy or diffuse, so its name became the diffuse series (see Figure SN-2).
    [Show full text]