Characterizing a Wavelength Shifter Coated Silicon Photomultiplier at Cryogenic Temperatures Using Scintillation Light in Gaseous Xenon
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

RADA Sense Mobile Application End-User Licence Agreement
RADA Sense Mobile Application End-User Licence Agreement PLEASE READ THESE LICENCE TERMS CAREFULLY BY CONTINUING TO USE THIS APP YOU AGREE TO THESE TERMS WHICH WILL BIND YOU. IF YOU DO NOT AGREE TO THESE TERMS, PLEASE IMMEDIATELY DISCONTINUE USING THIS APP. WHO WE ARE AND WHAT THIS AGREEMENT DOES We Kohler Mira Limited of Cromwell Road, Cheltenham, GL52 5EP license you to use: • Rada Sense mobile application software, the data supplied with the software, (App) and any updates or supplements to it. • The service you connect to via the App and the content we provide to you through it (Service). as permitted in these terms. YOUR PRIVACY Under data protection legislation, we are required to provide you with certain information about who we are, how we process your personal data and for what purposes and your rights in relation to your personal data and how to exercise them. This information is provided in https://www.radacontrols.com/en/privacy/ and it is important that you read that information. Please be aware that internet transmissions are never completely private or secure and that any message or information you send using the App or any Service may be read or intercepted by others, even if there is a special notice that a particular transmission is encrypted. APPLE APP STORE’S TERMS ALSO APPLY The ways in which you can use the App and Documentation may also be controlled by the Apple App Store’s rules and policies https://www.apple.com/uk/legal/internet-services/itunes/uk/terms.html and Apple App Store’s rules and policies will apply instead of these terms where there are differences between the two. -

English-P360-Deductible-Tool.Pdf
T-Mobile® Deductible and Fee Schedule Alcatel Tier BlackBerry Tier Huawei Tier 9810, 9900 3T 8 Comet Q10 665 3 Prism, Prism II Z10 768 Sonic 4G A30 Priv 4 Summit 1 Aspire Tap Evolve webConnect Fierce XL Coolpad Tier Fierce, Fierce 2, Fierce 4 1 Catalyst GO FLIP myTouch 2 LINKZONE Defiant Pixi 7 Rogue 1 S7 PRO 3 POP 7 Snap POP Astro Surf REVVL REVVL Plus 2 Kyocera Tier Soul Hydro WAVE 1 IDOL 4S 3 Dell Tier Rally Streak 7 2 DuraForce PRO, DuraForceXD 3 Apple Tier Ericsson Tier iPad iPad Air 2 World 1 LG Tier iPad Mini, iPad Mini 2, iPad Mini 4 450 iPhone 4, iPhone 4s 3 GARMIN Tier Aristo iPhone 5, iPhone 5c, iPhone 5s Aristo 2 PLUS iPhone 6s Garminfone 3 dLite iPhone SE GS170 Watch Series 3 1 GEOTAB Tier K7, K10 K20 Plus iPad Air SyncUP FLEET 1 Leon iPad Mini 3 Optimus L90 iPad Pro 9.7 Sentio iPhone 6 4 GOOGLE Tier iPhone 6s Plus Pixel 3a DoublePlay iPhone 7, iPhone 7 Plus Pixel 3a XL 3 Watch Series 4 G Pad F 8.0 G Pad X2 8.0, G Pad X2 8.0 Plus Pixel 3 4 G Pad X 8.0 iPad Pro 10.5-inch Pixel 3 XL G Stylo iPad Pro 11-inch G2 iPad Pro 12.9-inch G2x iPhone 6 Plus HTC Tier1 5 K30 2 iPhone 8, iPhone 8 Plus Desire iPhone X Lion iPhone XR myTouch iPhone XS, iPhone XS MAX Amaze 4G Optimus F3, F3Q, F6, L9, T Dash 3G Stylo 2 PLUS, Stylo 3 PLUS G2 Stylo 4 ASUS Tier HD2, HD7 V20 life Google Nexus 7 2 myTouch 3G 1.2, myTouch 3G slide 2 G3, G5, G6 myTouch 4G G-Slate One M9 Nexus 4, Nexus 5 3 BlackBerry Tier One S P Plus Radar 4G Q7+ 7100T, 7105T Shadow 7230, 7290 Wildfire S G Flex 8120, 8520 G7 9780 Bold 2 4 10 G8 Classic Flyer V30 Curve myTouch V10 myTouch 4G Slide 3 5 9700 Bold 3 One V30+ Sensation 4G Windows Phone 8X Please note: If you switch your device to one that is classified in another tier, the monthly charge for your new tier will be reflected on your T-Mobile bill. -

KONYKS Interrupteur Pour Volets Roulants Vollo KONYKS
KONYKS Interrupteur pour volets roulants Vollo KONYKS Contrôlez votre interrupteur à la voix ou à distance grâce à votre smartphone. GENCODE : 3770008652316 REF. : KONYVOLLO Caractéristiques Interrupteur pour volets roulants Vollo KONYKS : - Interrupteur encastrable pour volet roulants (installation filaire, fonctionne aussi pour rideaux motorisés) - Pilotage à la voix : avec Google Home ou Alexa vous pilotez les volets très simplement: «OK Google, ouvre les volets, Alexa ferme les volets» - Contrôle depuis son Smartphone, de n'importe où dans le monde grâce à l'appli Konyks iOS et Android - Automatisez facilement: Fermer les volets au coucher du soleil, ou à une heure précise, programmer ouverture et fermetures en votre absence, fermer les volets s'il gèle dehors etc.... - Spécifications techniques : Nécessite un réseau Wifi 2.4 Ghz 802.11 b/g/n AC 110-240 V - 50-60 Hz 3A 600W max Matériau ABS retardateur de flamme Application en français avec Widgets, Programmation horaire, compte à rebours, scénarios et automatisations, compatible raccourcis Siri Atout Compatible Google Home ou Alexa Fermeture automatique des volets programmée Compatible avec les smartphones sous Android 4.1 et versions ultérieures Compatibilité ou iOS 8 et versions ultérieures Dimensions 86 x 86 x 35 mm Couleur Blanc Poids net 148 g Contenu du pack 1 Interrupteur pour volets roulants Vollo KONYKS MOBILES COMPATIBLES ACER ICONIA TAB B1-A71 / LIQUID E1 / LIQUID E2 / LIQUID Z2 / LIQUID Z200 / LIQUID Z3 ALCATEL 1 (5033) / 1X (5059) / 1X 2019 (5008) / 3 (5052) / 3C (5026) -
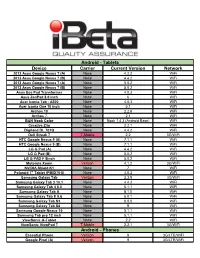
Ibeta-Device-Invento
Android - Tablets Device Carrier Current Version Network 2012 Asus Google Nexus 7 (A) None 4.2.2 WiFi 2012 Asus Google Nexus 7 (B) None 4.4.2 WiFi 2013 Asus Google Nexus 7 (A) None 5.0.2 WiFi 2013 Asus Google Nexus 7 (B) None 5.0.2 WiFi Asus Eee Pad Transformer None 4.0.3 WiFi Asus ZenPad 8.0 inch None 6 WiFi Acer Iconia Tab - A500 None 4.0.3 WiFi Acer Iconia One 10 inch None 5.1 WiFi Archos 10 None 2.2.6 WiFi Archos 7 None 2.1 WiFi B&N Nook Color None Nook 1.4.3 (Android Base) WiFi Creative Ziio None 2.2.1 WiFi Digiland DL 701Q None 4.4.2 WiFi Dell Streak 7 T-Mobile 2.2 3G/WiFi HTC Google Nexus 9 (A) None 7.1.1 WiFi HTC Google Nexus 9 (B) None 7.1.1 WiFi LG G Pad (A) None 4.4.2 WiFi LG G Pad (B) None 5.0.2 WiFi LG G PAD F 8inch None 5.0.2 WiFi Motorola Xoom Verizon 4.1.2 3G/WiFi NVIDIA Shield K1 None 7 WiFi Polaroid 7" Tablet (PMID701i) None 4.0.3 WiFi Samsung Galaxy Tab Verizon 2.3.5 3G/WiFi Samsung Galaxy Tab 3 10.1 None 4.4.2 WiFi Samsung Galaxy Tab 4 8.0 None 5.1.1 WiFi Samsung Galaxy Tab A None 8.1.0 WiFi Samsung Galaxy Tab E 9.6 None 6.0.1 WiFi Samsung Galaxy Tab S3 None 8.0.0 WiFi Samsung Galaxy Tab S4 None 9 WiFi Samsung Google Nexus 10 None 5.1.1 WiFi Samsung Tab pro 12 inch None 5.1.1 WiFi ViewSonic G-Tablet None 2.2 WiFi ViewSonic ViewPad 7 T-Mobile 2.2.1 3G/WiFi Android - Phones Essential Phone Verizon 9 3G/LTE/WiFi Google Pixel (A) Verizon 9 3G/LTE/WiFi Android - Phones (continued) Google Pixel (B) Verizon 8.1 3G/LTE/WiFi Google Pixel (C) Factory Unlocked 9 3G/LTE/WiFi Google Pixel 2 Verizon 8.1 3G/LTE/WiFi Google Pixel -
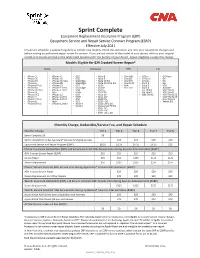
Sprint Complete
Sprint Complete Equipment Replacement Insurance Program (ERP) Equipment Service and Repair Service Contract Program (ESRP) Effective July 2021 This device schedule is updated regularly to include new models. Check this document any time your equipment changes and before visiting an authorized repair center for service. If you are not certain of the model of your phone, refer to your original receipt or it may be printed on the white label located under the battery of your device. Repair eligibility is subject to change. Models Eligible for $29 Cracked Screen Repair* Apple Samsung HTC LG • iPhone 5 • iPhone X • GS5 • Note 8 • One M8 • G Flex • G3 Vigor • iPhone 5C • iPhone XS • GS6 • Note 9 • One E8 • G Flex II • G4 • iPhone 5S • iPhone XS Max • GS6 Edge • Note 20 5G • One M9 • G Stylo • G5 • iPhone 6 • iPhone XR • GS6 Edge+ • Note 20 Ultra 5G • One M10 • Stylo 2 • G6 • iPhone 6 Plus • iPhone 11 • GS7 • GS10 • Bolt • Stylo 3 • V20 • iPhone 6S • iPhone 11 Pro • GS7 Edge • GS10e • HTC U11 • Stylo 6 • X power • iPhone 6S Plus • iPhone 11 Pro • GS8 • GS10+ • G7 ThinQ • V40 ThinQ • iPhone SE Max • GS8+ • GS10 5G • G8 ThinQ • V50 ThinQ • iPhone SE2 • iPhone 12 • GS9 • Note 10 • G8X ThinQ • V60 ThinQ 5G • iPhone 7 • iPhone 12 Pro • GS9+ • Note 10+ • V60 ThinQ 5G • iPhone 7 Plus • iPhone 12 Pro • A50 • GS20 5G Dual Screen • iPhone 8 Max • A51 • GS20+ 5G • Velvet 5G • iPhone 8 Plus • iPhone 12 Mini • Note 4 • GS20 Ultra 5G • Note 5 • Galaxy S20 FE 5G • GS21 5G • GS21+ 5G • GS21 Ultra 5G Monthly Charge, Deductible/Service Fee, and Repair Schedule -

Supported Android Smartphone and Tablet Devices
The following Google Android and Apple iOS smartphones and tablets have gone through testing and calibration, and provide the highest level of accuracy: Supported Android Smartphone and Tablet Devices Point- Photo Target Device to- Measure Location Point Asus ZenPad ✓ ✗ ✗ 3S 10 Supported for Photo Measure Asus but not ✓ ✗ ✗ Zenpad Z8 recommended for P2P or Target Location Asus Zenpad ✓ ✓ ✓ Z10 HTC One ✓ ✗ ✗ M8 HTC One ✓ ✗ ✗ Mini HTC U11 ✓ ✗ ✗ iNew L1 ✓ ✗ ✗ Kyocera Dura ✓ ✓ ✓ Force PRO Kyocera Dura ✓ ✓ ✓ Force PRO 2 LGV20 ✓ ✗ ✗ Supported for Motorola Photo Measure ✓ ✗ ✗ Moto G but not recommended Supported for Motorola Photo Measure Moto X ✓ ✗ ✗ but not XT1052 recommended Supported for Motorola Photo Measure Moto X ✓ ✗ ✗ but not XT1053 recommended Nexus 5 ✓ ✓ ✓ Nexus 5X ✓ ✓ ✓ * Supported for Nexus 6 ✓ ✓* ✓ Point-to-Point, but cannot guarantee +/-3% accuracy * Supported for Point-to-Point, but Nexus 6P ✓ ✓* ✓ cannot guarantee +/-3% accuracy * Supported for Point-to-Point, but Nexus 7 ✓ ✓* ✓ cannot guarantee +/-3% accuracy Samsung Galaxy ✓ ✓ ✓ A20 Samsung Galaxy J7 ✓ ✗ ✓ Prime * Supported for Samsung Point-to-Point, but GALAXY ✓ ✓* ✓ cannot guarantee Note3 +/-3% accuracy Samsung GALAXY ✓ ✓ ✓ Note 4 * Supported for Samsung Point-to-Point, but GALAXY ✓ ✓* ✓ cannot guarantee Note 5 +/-3% accuracy Samsung GALAXY ✓ ✓ ✓ Note 8 Samsung GALAXY ✓ ✓ ✓ Note 9 Samsung GALAXY ✓ ✓ ✓ Note 10 Samsung GALAXY ✓ ✓ ✓ Note 10+ Samsung GALAXY ✓ ✓ ✓ Note 10+ 5G Supported for Samsung Photo Measure GALAXY ✓ ✗ ✗ but not Tab 4 (old) recommended Samsung Supported for -

These Phones Will Still Work on Our Network After We Phase out 3G in February 2022
Devices in this list are tested and approved for the AT&T network Use the exact models in this list to see if your device is supported See next page to determine how to find your device’s model number There are many versions of the same phone, and each version has its own model number even when the marketing name is the same. ➢EXAMPLE: ▪ Galaxy S20 models G981U and G981U1 will work on the AT&T network HOW TO ▪ Galaxy S20 models G981F, G981N and G981O will NOT work USE THIS LIST Software Update: If you have one of the devices needing a software upgrade (noted by a * and listed on the final page) check to make sure you have the latest device software. Update your phone or device software eSupport Article Last updated: Sept 3, 2021 How to determine your phone’s model Some manufacturers make it simple by putting the phone model on the outside of your phone, typically on the back. If your phone is not labeled, you can follow these instructions. For iPhones® For Androids® Other phones 1. Go to Settings. 1. Go to Settings. You may have to go into the System 1. Go to Settings. 2. Tap General. menu next. 2. Tap About Phone to view 3. Tap About to view the model name and number. 2. Tap About Phone or About Device to view the model the model name and name and number. number. OR 1. Remove the back cover. 2. Remove the battery. 3. Look for the model number on the inside of the phone, usually on a white label. -

Device Compatibility
Device compatibility Check if your smartphone is compatible with your Rexton devices Direct streaming to hearing aids via Bluetooth Apple devices: Rexton Mfi (made for iPhone, iPad or iPod touch) hearing aids connect directly to your iPhone, iPad or iPod so you can stream your phone calls and music directly into your hearing aids. Android devices: With Rexton BiCore devices, you can now also stream directly to Android devices via the ASHA (Audio Streaming for Hearing Aids) standard. ASHA-supported devices: • Samsung Galaxy S21 • Samsung Galaxy S21 5G (SM-G991U)(US) • Samsung Galaxy S21 (US) • Samsung Galaxy S21+ 5G (SM-G996U)(US) • Samsung Galaxy S21 Ultra 5G (SM-G998U)(US) • Samsung Galaxy S21 5G (SM-G991B) • Samsung Galaxy S21+ 5G (SM-G996B) • Samsung Galaxy S21 Ultra 5G (SM-G998B) • Samsung Galaxy Note 20 Ultra (SM-G) • Samsung Galaxy Note 20 Ultra (SM-G)(US) • Samsung Galaxy S20+ (SM-G) • Samsung Galaxy S20+ (SM-G) (US) • Samsung Galaxy S20 5G (SM-G981B) • Samsung Galaxy S20 5G (SM-G981U1) (US) • Samsung Galaxy S20 Ultra 5G (SM-G988B) • Samsung Galaxy S20 Ultra 5G (SM-G988U)(US) • Samsung Galaxy S20 (SM-G980F) • Samsung Galaxy S20 (SM-G) (US) • Samsung Galaxy Note20 5G (SM-N981U1) (US) • Samsung Galaxy Note 10+ (SM-N975F) • Samsung Galaxy Note 10+ (SM-N975U1)(US) • Samsung Galaxy Note 10 (SM-N970F) • Samsung Galaxy Note 10 (SM-N970U)(US) • Samsung Galaxy Note 10 Lite (SM-N770F/DS) • Samsung Galaxy S10 Lite (SM-G770F/DS) • Samsung Galaxy S10 (SM-G973F) • Samsung Galaxy S10 (SM-G973U1) (US) • Samsung Galaxy S10+ (SM-G975F) • Samsung -
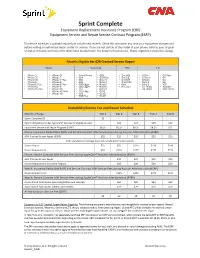
Sprint Complete Equipment Replacement Insurance Program (ERP) Equipment Service and Repair Service Contract Program (ESRP)
Sprint Complete Equipment Replacement Insurance Program (ERP) Equipment Service and Repair Service Contract Program (ESRP) This device schedule is updated regularly to include new models. Check this document any time your equipment changes and before visiting an authorized repair center for service. If you are not certain of the model of your phone, refer to your original receipt or it may be printed on the white label located under the battery of your device. Repair eligibility is subject to change. Models Eligible for $29 Cracked Screen Repair Apple Samsung HTC LG • iPhone 5 • iPhone SE • Grand Prime • GS9 • One M8 • G Flex • G3 Vigor • iPhone 5C • iPhone 7 • GS4 • GS9 Plus • One E8 • G Flex II • G4 • iPhone 5S • iPhone 7 Plus • GS5 • Note 3 • One M9 • G Stylo • G5 • iPhone 6 • iPhone 8 • GS6 • Note 4 • One M10 • Stylo 2 • G6 • iPhone 6 Plus • iPhone 8 Plus • GS6 Edge • Note 5 • Bolt • Stylo 3 • V20 • iPhone 6S • iPhone X • GS6 Edge+ • Note 8 • HTC U11 • G7 ThinQ • X power • iPhone 6S Plus • iPhone XS • GS7 • Note 9 • G8 ThinQ • V40 ThinQ • iPhone XS Max • GS7 Edge • GS10 • iPhone XR • GS8 • GS10e • GS8 Plus • GS10+ Deductible/Service Fee and Repair Schedule Monthly Charge Tier 1 Tier 2 Tier 3 Tier 4 Tier 5 Sprint Complete $9 $9 - - - - Sprint Complete (Includes AppleCare® Services for eligible devices) - $15 $15 $15 $19 Equipment Service and Repair Program (ESRP) $8.25 $8.25 $8.25 $8.25 $11 Phone: Insurance Deductibles (ERP) and Service Contract ADH Service Fees during Asurion Administration (ESRP) ADH Cracked Screen Repair (ESRP) $25 $29 $29 $29 $29 ESRP standalone coverage does not include $29 cracked screens. -
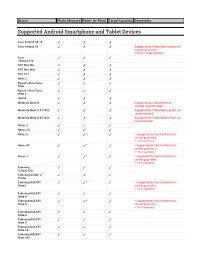
List of Supported Devices
Device Photo Measure Point- to- Point Target Location Comments Supported Android Smartphone and Tablet Devices Asus ZenPad 3S 10 ✓ ✗ ✗ Asus Zenpad Z8 ✓ ✗ ✗ Supported for Photo Measure but not recommended for P2P or Target Location Asus ✓ ✓ ✓ Zenpad Z10 HTC One M8 ✓ ✗ ✗ HTC One Mini ✓ ✗ ✗ HTC U11 ✓ ✗ ✗ iNew L1 ✓ ✗ ✗ Kyocera Dura Force ✓ ✓ ✓ PRO Kyocera Dura Force ✓ ✓ ✓ PRO 2 LGV20 ✓ ✗ ✗ Motorola Moto G ✓ ✗ ✗ Supported for Photo Measure but not recommended Motorola Moto X XT1052 ✓ ✗ ✗ Supported for Photo Measure but not recommended Motorola Moto X XT1053 ✓ ✗ ✗ Supported for Photo Measure but not recommended Nexus 5 ✓ ✓ ✓ Nexus 5X ✓ ✓ ✓ Nexus 6 ✓ ✓* ✓ * Supported for Point-to-Point, but cannot guarantee +/-3% accuracy Nexus 6P ✓ ✓* ✓ * Supported for Point-to-Point, but cannot guarantee +/-3% accuracy Nexus 7 ✓ ✓* ✓ * Supported for Point-to-Point, but cannot guarantee +/-3% accuracy Samsung ✓ ✓ ✓ Galaxy A20 Samsung Galaxy J7 ✓ ✗ ✓ Prime Samsung GALAXY ✓ ✓* ✓ * Supported for Point-to-Point, but Note3 cannot guarantee +/-3% accuracy Samsung GALAXY ✓ ✓ ✓ Note 4 Samsung GALAXY ✓ ✓* ✓ * Supported for Point-to-Point, but Note 5 cannot guarantee +/-3% accuracy Samsung GALAXY ✓ ✓ ✓ Note 8 Samsung GALAXY ✓ ✓ ✓ Note 9 Samsung GALAXY ✓ ✓ ✓ Note 10 Samsung GALAXY ✓ ✓ ✓ Note 10+ Device Photo Measure Point- to- Point Target Location Comments Samsung GALAXY ✓ ✓ ✓ Note 10+ 5G Samsung GALAXY ✓ ✓ ✓ Note 20 Samsung GALAXY ✓ ✓ ✓ Note 20 5G Samsung GALAXY ✓ ✗ ✗ Supported for Photo Measure but not Tab 4 (old) recommended Samsung GALAXY ✓ ✗ ✓ Supported for Photo -

English-Basic-Deductible-Tool.Pdf
T-Mobile® Deductible and Fee Schedule Alcatel Tier BlackBerry Tier HTC Tier 3T 8 7100T, 7105T 10 665 7230, 7290 Flyer 768 8120, 8520 myTouch 2 A30 9780 Bold myTouch 4G Slide 3 Aspire Classic One Evolve Curve Sensation 4G Fierce XL Windows Phone 8X Fierce, Fierce 2, Fierce 4 9700 Bold 1 GO FLIP, GO FLIP 3 9810, 9900 3 JOY TAB Q10 Huawei Tier LINKZONE, LINKZONE 2 Z10 Comet Pixi 7 Prism, Prism II POP 7 Priv 4 Sonic 4G POP Astro 1 REVVL Coolpad Tier Summit Soul Tap Catalyst webConnect JOY TAB Kids 2 Defiant Rogue 1 myTouch 2 IDOL 4S 3 Snap S7 PRO 3 Surf Apple Tier life KonnectONE Tier 2 iPad One M9 Moxee Signal 1 iPad 7th Gen iPad Air 2 Dell Tier iPad Mini, iPad Mini 2, iPad Mini 4 Kyocera Tier Streak 7 2 iPhone 4, iPhone 4s iPhone 5, iPhone 5c, iPhone 5s 3 Hydro WAVE Ericsson Tier 1 iPhone 6s Rally iPhone SE World 1 DuraForce PRO, DuraForceXD 3 Watch Series 3 Watch Series 5 Garmin Tier LG Tier iPad Air Garminfone 3 iPad Mini 3 450 iPad Pro 9.7 GEOTAB Tier Aristo iPhone 6 Aristo 2 PLUS 4 GO8 iPhone 6 Plus 1 Aristo 4+ iPhone 6s Plus SyncUP FLEET Aristo 5 dLite iPhone 7, iPhone 7 Plus 1 Watch Series 4 Google Tier GS170 Pixel 3a K7, K10 iPad Pro 10.5-inch 3 K20 Plus Pixel 3a XL iPad Pro 11-inch Leon iPad Pro 12.9-inch Pixel 3 Optimus L90 iPhone 8, iPhone 8 Plus Sentio iPhone X Pixel 3 XL 4 5 iPhone XR Pixel 4 DoublePlay iPhone XS, iPhone XS MAX Pixel 4 XL 5 G Pad 5 iPhone 11 G Pad F 8.0 iPhone 11 Pro, iPhone 11 Pro Max HTC Tier G Pad X2 8.0, G Pad X2 8.0 Plus Watch Nike+ Series 3 G Pad X 8.0 Desire 1 G Stylo G2 ASUS Tier Amaze 4G G2x Dash 3G Google Nexus 7 2 K30 G2 K40 2 HD2, HD7 K51 life Lion myTouch 3G 1.2, myTouch 3G slide 2 myTouch myTouch 4G Optimus F3, F3Q, F6, L9, T One M9 Stylo 2 PLUS, Stylo 3 PLUS One S Stylo 4 Radar 4G Stylo 5 Shadow Stylo 6 Wildfire S V20 Please note: If you switch your device to one that is classified in another tier, the monthly charge for your new tier will be reflected on your T-Mobile bill. -

Lumify V1.8 Device Compatibility List
Lumify v1.8 Device Compatibility List Supported Devices* Approximate Supports Reacts Screen Internal Device Name Connectivity Options Continuous Scan USB Size Storage Time Type Samsung Galaxy Tab S6 (Model SM-T860) 10.5 in Wi-Fi 128 GB TBD C Yes Samsung Galaxy Tab S4 (Model SM-T830, SM-T835, SM-T837) 10.5 in Wi-Fi or Wi-Fi/LTE 64 GB 5 h 30 min C Yes Samsung Galaxy Tab A -2018 (Model SM-T590, SM-T595) 10.5 in Wi-Fi /LTE 32 GB 3 h 38 min C Yes Samsung Galaxy Tab A- 2018 (Model SM-T387) 8.0 in Wi-Fi /LTE 32 GB 3 h 29 min B Yes Samsung Galaxy S10e (SM-G970U) 5.8 in Wi-Fi / LTE 128 GB 4 h 7 min C Yes Samsung Galaxy S10 (SM-G973U) 6.1 in Wi-Fi / LTE 128 GB 4 h 3 min C Yes Samsung Galaxy S10+ (SM-G975U) 6.4 in Wi-Fi / LTE 128 GB 3 h 34 min C Yes Samsung Galaxy S9 (SM-G960U) 5.8 in Wi-Fi / LTE 32 GB 3 h 45 min C Yes Samsung Galaxy S9+ (SM-G965U) 6.2 in Wi-Fi / LTE 64 GB 4 h C Yes Samsung Galaxy Note10+ (SM-N975U) 6.8 in Wi-Fi / LTE 256 GB TBD C Yes Samsung Galaxy Note10 (SM-970U) 6.3 in Wi-Fi / LTE 256 GB TBD C Yes Samsung Galaxy Note9 (SM-N960U) 6.25 in Wi-Fi / LTE 128 GB 3 h 26 min C Yes Samsung Galaxy Note8 (SM-N950U) 6.3 in Wi-Fi / LTE 64 GB 3 h 30 min C Yes Samsung Galaxy S8 (SM-G950U) 5.8 in Wi-Fi / LTE 32 GB 3 h 30 min C Yes Samsung Galaxy S8+ (SM-G955U) 6.2 in Wi-Fi / LTE 64 GB 4 h C Yes 5.6 in/ C Yes Google Pixel 3a / Pixel 3a XL Wi-Fi / LTE 64 GB 3 h 26 min 6.0 in 5.5 in/ C Yes Google Pixel 3 / Pixel 3 XL Wi-Fi 64 GB 3 h 43 min 6.3 in Samsung Galaxy Tab S2 8” (Only Model SM-T713) 8 in Wi-Fi 32 GB 2 h 30 min B Yes Panasonic Toughpad FZ-A2 10.1 in Wi-Fi/LTE 32 GB 3 h 30 min C Yes Panasonic Toughpad FZ-B2 (USB C models only) 7 in Wi-Fi/LTE 32 GB 3 h 30 min C Yes Philips Ultrasound, Inc.