DOCSLIB.ORG

Electrochemistry a Chem1 Supplement Text Stephen K

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Electrochemistry a Chem1 Supplement Text Stephen K Electrochemistry a Chem1 Supplement Text Stephen K. Lower Simon Fraser University Contents 1 Chemistry and electricity 2 Electroneutrality .............................. 3 Potential dierences at interfaces ..................... 4 2 Electrochemical cells 5 Transport of charge within the cell .................... 7 Cell description conventions ........................ 8 Electrodes and electrode reactions .................... 8 3 Standard half-cell potentials 10 Reference electrodes ............................ 12 Prediction of cell potentials ........................ 13 Cell potentials and the electromotive series ............... 14 Cell potentials and free energy ...................... 15 The fall of the electron ........................... 17 Latimer diagrams .............................. 20 4 The Nernst equation 21 Concentration cells ............................. 23 Analytical applications of the Nernst equation .............. 23 Determination of solubility products ................ 23 Potentiometric titrations ....................... 24 Measurement of pH .......................... 24 Membrane potentials ............................ 26 5 Batteries and fuel cells 29 The fuel cell ................................. 29 1 CHEMISTRY AND ELECTRICITY 2 6 Electrochemical Corrosion 31 Control of corrosion ............................ 34 7 Electrolytic cells 34 Electrolysis involving water ........................ 35 Faraday’s laws of electrolysis ....................... 36 Industrial electrolytic processes ...................... 37 The chloralkali industry. ....................... 37 Electrolytic rening of aluminum .................. 38 1 Chemistry and electricity The connection between chemistry and electricity is a very old one, going back to Allesandro Volta’s discovery, in 1793, that electricity could be produced by placing two dissimilar metals on opposite sides of a moistened paper. In 1800, Nicholson and Carlisle, using Volta’s primitive battery as a source, showed that an electric current could decompose water into oxygen and hydrogen. This was surely one of the most signicant experiments in the history of chemistry, for it implied that the atoms of hydrogen and oxygen were associated with positive and negative electric charges, which must be the source of the bonding forces between them. By 1812, the Swedish chemist Berzelius could propose that all atoms are electried, hydrogen and the metals being positive, the nonmetals negative. In electrolysis, the applied voltage was thought to overpower the attraction between these opposite charges, pulling the electried atoms apart in the form of ions (named by Berzelius from the Greek for “travellers”). It would be almost exactly a hundred years later before the shared electron pair theory of G.N. Lewis could oer a signicant improvement over this view of chemical bonding. 1 CHEMISTRY AND ELECTRICITY 3 dissoluti on of Zn as Zn2+ causes - electric charges to build up in the - - tw o phases which inhibi ts further e e AAZn dissoluti on AAA AA AAA Zn2+(aq) AA AAA AA Zn2+(aq) AAA AA Zn in metal Figure 1: Oxidation of metallic zinc in contact with water Meanwhile, the use of electricity as a means of bringing about chemical change continued to play a central role in the development of chemistry. Humphrey Davey prepared the rst elemental sodium by electrolysis of a sodium hydrox- ide melt. It was left to Davey’s former assistant, Michael Faraday, to show that there is a quantitative relation between the amount of electric charge and the quantity of electrolysis product. James Clerk Maxwell immediately saw this as evidence for the “molecule of electricity”, but the world would not be receptive to the concept of the electron until the end of the century. Electroneutrality Nature seems to very strongly discourage any process that would lead to an excess of positive or negative charge in matter. Suppose, for example, that we immerse a piece of zinc metal in pure water. A small number of zinc atoms go into solution as Zn2+ ions, leaving their electrons behind in the metal: 2+ Zn(s) Zn +2e (1) → As this process goes on, the electrons which remain in the zinc cause a negative charge to build up which makes it increasingly dicult for additional positive ions to leave the metallic phase. A similar buildup of positive charge in the liquid phase adds to this inhibition. Very soon, therefore, the process comes to a halt, resulting in a solution in which the concentration of Zn2+ is so low 10 (around 10 M ) that the water can still be said to be almost “pure”. There would be no build-up of charge if the electrons could be removed from the metal as the positive ions go into solution. One way to arrange this is to drain o the excess electrons through an external circuit that forms part of a complete electrochemical cell; this we will describe later. Another way to remove electrons is to bring a good electron acceptor (that is, an oxidizing agent) into contact with the electrode. A 1 CHEMISTRY AND ELECTRICITY 4 suitable electron acceptor would be hydrogen ions; this is why acids attack many metals. For the very active metals such as sodium, H2O is a suciently good electron acceptor. The degree of charge unbalance that is allowed produces dierences in elec- tric potential of no more than a few volts, and corresponds to concentration un- balances of oppositely charged particles that are not even detectable by ordinary chemical means. There is nothing mysterious about this prohibition, known as the electroneutrality principle; it is a simple consequence of the thermodynamic work required to separate opposite charges, or to bring like charges into closer contact. The additional work raises the free energy G of the process, making it less spontaneous. The only way we can get the reaction in Eq 1 to continue is to couple it with some other process that restores electroneutrality to the two phases. A simple way to accomplish this would be immerse the zinc in a solution of copper sulfate instead of pure water. As you will recall if you have seen this commonly-performed experiment carried out, the zinc metal quickly becomes covered with a black coating of nely-divided metallic copper. The reaction is a simple oxidation-reduction process, a transfer of two electrons from the zinc to the copper: 2+ 2+ Zn(s) Zn +2e Cu +2e Cu(s) → → The dissolution of the zinc is no longer inhibited by a buildup of negative charge in the metal, because the excess electrons are removed from the zinc by copper ions that come into contact with it. At the same time, the solution remains electrically neutral, since for each Zn2+ introduced to the solution, one Cu2+ is removed. The net reaction Zn(s) +Cu2+ Zn2+ +Cu(s) → quickly goes to completion. Potential dierences at interfaces Electrochemistry is the study of reactions in which charged particles (ions or electrons) cross the interface between two phases of matter, typically a metallic phase (the electrode) and a conductive solution, or electrolyte. A process of this kind is known generally as an electrode process. Electrode processes (reactions) take place at the surface of the electrode, and produce a slight unbalance in the electric charges of the electrode and the solution. The result is an interfacial potential dierence which, as we saw above, can materially aect the rate and direction of the reaction. Much of the impor- tance of electrochemistry lies in the ways that these potential dierences can be related to the thermodynamics and kinetics of electrode reactions. In particular, 2 ELECTROCHEMICAL CELLS 5 Ð + direction of electron flow in external circuit AAA AAACu direction of conventional current flow Zn porous fritted AAA gl ass barrier AAA AAA A AAA Cu2+ AAAZn2+ A AAA AAA A AAA NO Ð 2+ Ð 2+ Ð AAA A 3 AAA Zn ê Zn ,NO3 êê Cu , NO3 ê Cu A Figure 2: A simple electrochemical cell manipulation of the interfacial potential dierence aords an important way of exerting external control on an electrode reaction. The interfacial potential dierences which develop in electrode-solution sys- tems are limited to only a few volts at most. This may not seem like very much, but it is important to understand that what is important is the distance over which this potential dierence exists. In the case sof an electrode immersed in a solution, this distance corresponds to the thin layer of water molecules and ions that attach themselves to the electrode surface– normally only a few atomic diamters.a only a few atomic diameters. In this way a very small voltage can produce a very large potential gradient For example, a potential dierence of 8 one volt across a thickness of only 10 cm amounts to a potential gradient of 100 million volts per centimetre: a very signicant value indeed! Actually, interfacial potentials exist between any two phases in contact, even in the absence of chemical reactions. In many forms of matter, they are the result of adsorption or ordered alignment of molecules caused by non-uniform forces in the interfacial region. Thus colloidal particles in aqueous suspenctions selectively adsorb a given kind of ion, positive for some colloids, and negative for others. The resulting net electric charge prevents the particles from coming together and coalescing, which they would otherwise tend to do under the inuence of ordinary van der Waals attractions. 2 Electrochemical cells The electron-transfer reactions that occur at the surface of a metal immersed in a solution take place near the surface of the electrode, so there is no way that the electrons passing between the solution and the electrode can be channeled through an instrument to measure their voltage or to control the rate of the reaction. However, if we have two such metal-solution interfaces, we can easily measure a potential diference between them. Such an arrangement is called a 2 ELECTROCHEMICAL CELLS 6 galvanic cell. A typical cell might consists of two pieces of metal, one zinc and the other copper, each immersed each in a solution containing a dissolved salt of the corresponding metal (see Fig. 2). The two solutions are connected by a tube containing a porous barrier that prevents them from rapidly mixing but allows ions to diuse through.
Load more

Recommended publications
  • Chapter 9 Titrimetric Methods 413
    Chapter 9 Titrimetric Methods Chapter Overview Section 9A Overview of Titrimetry Section 9B Acid–Base Titrations Section 9C Complexation Titrations Section 9D Redox Titrations Section 9E Precipitation Titrations Section 9F Key Terms Section 9G Chapter Summary Section 9H Problems Section 9I Solutions to Practice Exercises Titrimetry, in which volume serves as the analytical signal, made its first appearance as an analytical method in the early eighteenth century. Titrimetric methods were not well received by the analytical chemists of that era because they could not duplicate the accuracy and precision of a gravimetric analysis. Not surprisingly, few standard texts from the 1700s and 1800s include titrimetric methods of analysis. Precipitation gravimetry developed as an analytical method without a general theory of precipitation. An empirical relationship between a precipitate’s mass and the mass of analyte— what analytical chemists call a gravimetric factor—was determined experimentally by taking a known mass of analyte through the procedure. Today, we recognize this as an early example of an external standardization. Gravimetric factors were not calculated using the stoichiometry of a precipitation reaction because chemical formulas and atomic weights were not yet available! Unlike gravimetry, the development and acceptance of titrimetry required a deeper understanding of stoichiometry, of thermodynamics, and of chemical equilibria. By the 1900s, the accuracy and precision of titrimetric methods were comparable to that of gravimetric methods, establishing titrimetry as an accepted analytical technique. 411 412 Analytical Chemistry 2.0 9A Overview of Titrimetry We are deliberately avoiding the term In titrimetry we add a reagent, called the titrant, to a solution contain- analyte at this point in our introduction ing another reagent, called the titrand, and allow them to react.
    [Show full text]
  • The Practice of Chemistry Education (Paper)
    CHEMISTRY EDUCATION: THE PRACTICE OF CHEMISTRY EDUCATION RESEARCH AND PRACTICE (PAPER) 2004, Vol. 5, No. 1, pp. 69-87 Concept teaching and learning/ History and philosophy of science (HPS) Juan QUÍLEZ IES José Ballester, Departamento de Física y Química, Valencia (Spain) A HISTORICAL APPROACH TO THE DEVELOPMENT OF CHEMICAL EQUILIBRIUM THROUGH THE EVOLUTION OF THE AFFINITY CONCEPT: SOME EDUCATIONAL SUGGESTIONS Received 20 September 2003; revised 11 February 2004; in final form/accepted 20 February 2004 ABSTRACT: Three basic ideas should be considered when teaching and learning chemical equilibrium: incomplete reaction, reversibility and dynamics. In this study, we concentrate on how these three ideas have eventually defined the chemical equilibrium concept. To this end, we analyse the contexts of scientific inquiry that have allowed the growth of chemical equilibrium from the first ideas of chemical affinity. At the beginning of the 18th century, chemists began the construction of different affinity tables, based on the concept of elective affinities. Berthollet reworked this idea, considering that the amount of the substances involved in a reaction was a key factor accounting for the chemical forces. Guldberg and Waage attempted to measure those forces, formulating the first affinity mathematical equations. Finally, the first ideas providing a molecular interpretation of the macroscopic properties of equilibrium reactions were presented. The historical approach of the first key ideas may serve as a basis for an appropriate sequencing of
    [Show full text]
  • The History of the Concept of Element, with Particular Reference to Humphry Davy
    The Physical Sciences Initiative The history of the concept of element, with particular reference to Humphry Davy One of the problems highlighted when the recently implemented chemistry syllabus was being developed was the difficulty caused by starting the teaching of the course with atoms. The new syllabus offers a possible alternative teaching order that starts at the macroscopic level, and deals with elements. If this is done, the history of the idea of elements is dealt with at a very early stage. The concept of element originated with the ancient Greeks, notably Empedocles, who around 450 BC defined elements as the basic building blocks from which all other materials are made. He stated that there were four elements: earth, air, fire and water. Substances were said to change when elements break apart and recombine under the action of the forces of strife and love. Little progress was made in this area until the seventeenth century AD. The fruitless attempts of the alchemists to change base metals such as lead into gold and to find the “elixir of life” held back progress, although much chemical knowledge and expertise was gained. In 1661, 1 The Physical Sciences Initiative The Physical Sciences Initiative Robert Boyle defined an element as a substance that cannot be broken down into simpler materials. He cast doubt on the Greek elements, and provided a criterion for showing that a material was not an element. Robert Boyle Many elements were discovered during the next 100 years, but progress was delayed by the phlogiston hypothesis. According to this hypothesis, when a substance was burned it lost a substance called phlogiston to the air.
    [Show full text]
  • Electrolytic Cells
    CHEMISTRY LEVEL 4C (CHM415115) ELECTROLYTIC CELLS THEORY SUMMARY & REVISION QUESTIONS (CRITERION 5) ©JAK DENNY Tasmanian TCE Chemistry Revision Guides by Jak Denny are licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License. INDEX: PAGES • INTRODUCTORY THEORY 3 • COMPARING ENERGY CONVERSIONS 4 • APPLICATIONS OF ELECTROLYSIS 4 • ELECTROPLATING 5 • COMPARING CELLS 6 • THE ELECTROCHEMICAL SERIES 7 • PREDICTING ELECTROLYSIS PRODUCTS 8-9 • ELECTROLYSIS PREDICTION FLOWCHART 1 0 • ELECTROLYSIS PREDICTION EXAMPLES 11 • ELECTROLYSIS PREDICTION QUESTIONS 12 • INDUSTRIAL ELECTROLYTIC PROCESSES 13 • IMPORTANT ELECTRICAL THEORY 14 • FARADAY’S ELECTROLYSIS LAWS 15 • QUANTITATIVE ELECTROLYSIS 16 • CELLS IN SERIES 17 • ELECTROLYSIS QUESTIONS 18-20 • ELECTROLYSIS TEST QUESTIONS 21-22 • TEST ANSWERS 23 2 ©JAK CHEMISTRY LEVEL 4C (CHM415115) ELECTROLYTIC CELLS (CRITERION 5) INTRODUCTION: In our recent investigation of electrochemical cells, we encountered spontaneous redox reactions that release electrical energy such as takes place in the familiar situations of “batteries”. When a car battery is ‘flat’ and needs to be recharged, a power supply (‘battery charger’) is connected to the flat battery and chemical changes take place and it is subsequently able to operate again as a power supply. The ‘recharging’ process is non-spontaneous and requires an input of energy to occur. When a cell is such that an energy input is required to make a non-spontaneous redox reaction take place, we describe the cell as an ELECTROLYTIC CELL. The redox process occurring in an ELECTROLYTIC CELL is referred to as ELECTROLYSIS. For example, consider the spontaneous redox reaction associated with an electrochemical (fuel) cell; i.e. 2H2(g) + O2(g) → 2H2O(l) + ELECTRICAL ENERGY This chemical reaction RELEASES energy which can be used to power an electric motor, to drive a machine, appliance or car.
    [Show full text]
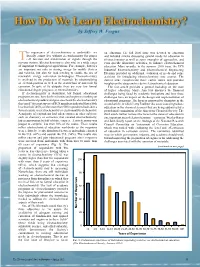
  • How Do We Learn Electrochemistry? by Jeffrey W
    redcat_ad_IF_Sp2012_1.pdf 1 4/11/2012 1:36:17 PM research • news • events • resources | search • explore • connect • share • discover How Do We Learn Electrochemistry? by Jeffrey W. Fergus he importance of electrochemistry is undeniable—we on education. The fall 2006 issue was devoted to education literally cannot live without electrochemistry for proper and included articles discussing general needs for education in Tcell function and transmission of signals through the electrochemistry as well as some examples of approaches, and nervous system. Electrochemistry is also vital in a wide range even specific laboratory activities, to enhance electrochemical of important technological applications. For example, batteries education. More recently, in the summer 2010 issue, the ECS are important not only in storing energy for mobile devices Industrial Electrochemistry and Electrochemical Engineering and vehicles, but also for load leveling to enable the use of Division provided an additional evaluation of needs and some renewable energy conversion technologies. Electrochemistry activities for introducing electrochemistry into courses. The is involved in the production of materials by electrorefining current issue complements those earlier issues and provides or electrodeposition as well as the destruction of materials by insights on the status and needs in electrochemical education. TM corrosion. In spite of its ubiquity there are very few formal The first article provides a general backdrop on the state educational degree programs in electrochemistry. of higher education. Marye Ann Fox discusses the financial If electrochemistry is ubiquitous, but formal educational challenges being faced by academic institutions and how these programs are rare, how do the scientists and engineers working on challenges have an impact on the design and implementation of electrochemical products and processes learn the electrochemistry educational programs.
    [Show full text]
  • Acid-Base Concentration Cell for Electric Power Generation
    Europaisches Patentamt J European Patent Office 0 Publication number: 0613199 A1 Office europeen des brevets EUROPEAN PATENT APPLICATION 0 Application number: 94101725.3 0 int. CI A H01M 8/22, H01M 14/00, H01 M 6/24 0 Date of filing: 04.02.94 0 Priority: 22.02.93 US 21417 0 Applicant: Hughes Aircraft Company 7200 Hughes Terrace, 0 Date of publication of application: P.O. Box 80028 31.08.94 Bulletin 94/35 Los Angeles, California 90080-0028 (US) 0 Designated Contracting States: 0 Inventor: Ludwig, Frank A. DE FR GB 29443 Whitley Collins Rancho Palos Verdes, California (US) 0 Representative: KUHNEN, WACKER & PARTNER Alois-Steinecker-Strasse 22 D-85354 Freising (DE) 0 Acid-base concentration cell for electric power generation. 0 An electric power system particularly adapted for use in powering the electric motor or motors used in the drive train of an electric vehicle. The power system includes a power cell which is a continuous flow concentration cell which utilizes the electrochemical reaction between an acid electrolyte (11) and a base electrolyte (13) to produce electrical energy. Both the acid and base electrolyte utilized in the power cell are kept in external reservoirs (10,12). The use of external reservoirs for the electrolytes provides for increases in the energy of the system which is only limited by the size of the reservoirs. Recharging of the system is quickly and conveniently accomplished by recharging the reservoirs with fresh electrolyte, or by electrically recharging the system. Rank Xerox (UK) Business Services (3. 10/3.09/3.3.4) EP 0 613 199 A1 BACKGROUND OF THE INVENTION 1_.
    [Show full text]
  • Electrochemical Real-Time Mass Spectrometry: a Novel Tool for Time-Resolved Characterization of the Products of Electrochemical Reactions
    Electrochemical real-time mass spectrometry: A novel tool for time-resolved characterization of the products of electrochemical reactions Elektrochemische Realzeit-Massenspektrometrie: Eine neuartige Methode zur zeitaufgelösten Charakterisierung der Produkte elektrochemischer Reaktionen Der Technischen Fakultät der Friedrich-Alexander-Universität Erlangen-Nürnberg zur Erlangung des Doktorgrades Dr.-Ingenieur vorgelegt von Peyman Khanipour Mehrin aus Shiraz, Iran Als Dissertation genehmigt von der Technischen Fakultät der Friedrich-Alexander-Universität Erlangen-Nürnberg Tag der mündlichen Prüfung: 17.11.2020 Vorsitzender des Promotionsorgans: Prof. Dr.-Ing. habil. Andreas Paul Fröba Gutachter: Prof. Dr. Karl J.J. Mayrhofer Prof. Dr. Frank-Michael Matysik I Acknowledgements This study is done in the electrosynthesis team of the electrocatalysis unit at Helmholtz- Institut Erlangen-Nürnberg (HI ERN) with the financial support of Forschungszentrum Jülich. I would like to express my deep gratitude to Prof. Dr. Karl J. J. Mayrhofer for accepting me as a Ph.D. student and also for all his encouragement, supports, and freedoms during my study. I’m grateful to Prof. Dr. Frank-Michael Matysik for kindly accepting to act as a second reviewer and also for the time he has invested in reading this thesis. This piece of work is enabled by collaboration with scientists from different expertise. I would like to express my appreciation to Dr. Sandra Haschke from FAU for providing shape-controlled high surface area platinum electrodes which I used for performing oxidation of primary alcohols and also the characterization of the provided material SEM, EDX, and XRD. Mr. Mario Löffler from HI ERN for obtaining the XPS data and his remarkable knowledge with the interpretation of the spectra on copper-based electrodes for the CO 2 electroreduction reaction.
    [Show full text]
  • Electrochemical Cells
    Electrochemical cells = electronic conductor If two different + surrounding electrolytes are used: electrolyte electrode compartment Galvanic cell: electrochemical cell in which electricity is produced as a result of a spontaneous reaction (e.g., batteries, fuel cells, electric fish!) Electrolytic cell: electrochemical cell in which a non-spontaneous reaction is driven by an external source of current Nils Walter: Chem 260 Reactions at electrodes: Half-reactions Redox reactions: Reactions in which electrons are transferred from one species to another +II -II 00+IV -II → E.g., CuS(s) + O2(g) Cu(s) + SO2(g) reduced oxidized Any redox reactions can be expressed as the difference between two reduction half-reactions in which e- are taken up Reduction of Cu2+: Cu2+(aq) + 2e- → Cu(s) Reduction of Zn2+: Zn2+(aq) + 2e- → Zn(s) Difference: Cu2+(aq) + Zn(s) → Cu(s) + Zn2+(aq) - + - → 2+ More complex: MnO4 (aq) + 8H + 5e Mn (aq) + 4H2O(l) Half-reactions are only a formal way of writing a redox reaction Nils Walter: Chem 260 Carrying the concept further Reduction of Cu2+: Cu2+(aq) + 2e- → Cu(s) In general: redox couple Ox/Red, half-reaction Ox + νe- → Red Any reaction can be expressed in redox half-reactions: + - → 2 H (aq) + 2e H2(g, pf) + - → 2 H (aq) + 2e H2(g, pi) → Expansion of gas: H2(g, pi) H2(g, pf) AgCl(s) + e- → Ag(s) + Cl-(aq) Ag+(aq) + e- → Ag(s) Dissolution of a sparingly soluble salt: AgCl(s) → Ag+(aq) + Cl-(aq) − 1 1 Reaction quotients: Q = a − ≈ [Cl ] Q = ≈ Cl + a + [Ag ] Ag Nils Walter: Chem 260 Reactions at electrodes Galvanic cell:
    [Show full text]
  • Analytical Chemistry Laboratory Manual 2
    ANALYTICAL CHEMISTRY LABORATORY MANUAL 2 Ankara University Faculty of Pharmacy Department of Analytical Chemistry Analytical Chemistry Practices Contents INTRODUCTION TO QUANTITATIVE ANALYSIS ......................................................................... 2 VOLUMETRIC ANALYSIS .............................................................................................................. 2 Volumetric Analysis Calculations ................................................................................................... 3 Dilution Factor ................................................................................................................................ 4 Standard Solutions ........................................................................................................................... 5 Primary standard .............................................................................................................................. 5 Characteristics of Quantitative Reaction ......................................................................................... 5 Preparation of 1 L 0.1 M HCl Solution ........................................................................................... 6 Preparation of 1 L 0.1 M NaOH Solution ....................................................................................... 6 NEUTRALIZATION TITRATIONS ...................................................................................................... 7 STANDARDIZATION OF 0.1 N NaOH SOLUTION ......................................................................
    [Show full text]
  • Chapter 10 – Chemical Reactions Notes
    Chapter 8 – Chemical Reactions Notes Chemical Reactions: Chemical reactions are processes in which the atoms of one or more substances are rearranged to form different chemical compounds. How to tell if a chemical reaction has occurred (recap): Temperature changes that can’t be accounted for. o Exothermic reactions give off energy (as in fire). o Endothermic reactions absorb energy (as in a cold pack). Spontaneous color change. o This happens when things rust, when they rot, and when they burn. Appearance of a solid when two liquids are mixed. o This solid is called a precipitate. Formation of a gas / bubbling, as when vinegar and baking soda are mixed. Overall, the most important thing to remember is that a chemical reaction produces a whole new chemical compound. Just changing the way that something looks (breaking, melting, dissolving, etc) isn’t enough to qualify something as a chemical reaction! Balancing Equations Notes: Things to keep in mind when looking at the recipes for chemical reactions: 1) The stuff before the arrow is referred to as the “reactants” or “reagents”, and the stuff after the arrow is called the “products.” 2) The number of atoms of each element is the same on both sides of the arrow. Even though there may be different numbers of molecules, the number of atoms of each element needs to remain the same to obey the law of conservation of mass. 3) The numbers in front of the formulas tell you how many molecules or moles of each chemical are involved in the reaction. 4) Equations are nothing more than chemical recipes.
    [Show full text]
  • Analytical Chemistry in the 21St Century: Challenges, Solutions, and Future Perspectives of Complex Matrices Quantitative Analyses in Biological/Clinical Field
    Review Analytical Chemistry in the 21st Century: Challenges, Solutions, and Future Perspectives of Complex Matrices Quantitative Analyses in Biological/Clinical Field 1, 2, 2, 3 Giuseppe Maria Merone y, Angela Tartaglia y, Marcello Locatelli * , Cristian D’Ovidio , Enrica Rosato 3, Ugo de Grazia 4 , Francesco Santavenere 5, Sandra Rossi 5 and Fabio Savini 5 1 Department of Neuroscience, Imaging and Clinical Sciences, University of Chieti–Pescara “G. d’Annunzio”, Via dei Vestini 31, 66100 Chieti, Italy; [email protected] 2 Department of Pharmacy, University of Chieti-Pescara “G. d’Annunzio”, Via Dei Vestini 31, 66100 Chieti (CH), Italy; [email protected] 3 Section of Legal Medicine, Department of Medicine and Aging Sciences, University of Chieti–Pescara “G. d’Annunzio”, 66100 Chieti, Italy; [email protected] (C.D.); [email protected] (E.R.) 4 Laboratory of Neurological Biochemistry and Neuropharmacology, Fondazione IRCCS Istituto Neurologico Carlo Besta, Via Celoria 11, 20133 Milano, Italy; [email protected] 5 Pharmatoxicology Laboratory—Hospital “Santo Spirito”, Via Fonte Romana 8, 65124 Pescara, Italy; [email protected] (F.S.); [email protected] (S.R.); [email protected] (F.S.) * Correspondence: [email protected]; Tel.: +39-0871-3554590; Fax: +39-0871-3554911 These authors contributed equally to the work. y Received: 16 September 2020; Accepted: 16 October 2020; Published: 30 October 2020 Abstract: Nowadays, the challenges in analytical chemistry, and mostly in quantitative analysis, include the development and validation of new materials, strategies and procedures to meet the growing need for rapid, sensitive, selective and green methods.
    [Show full text]
  • Chemistry - B.S
    Chemistry - B.S. College of (Biochemistry Option) Arts and Sciences The Department of Chemistry offers the Bachelor of Science degree for students who Graduation Composition and Communication Requirement intend to become professional chemists or do graduate work in chemistry or a closely (GCCR) related discipline. There are three options in the B.S. program: a traditional track WRD 310 Writing in the Natural Sciences ............................................................. 3 covering all the major areas of chemistry, an option that emphasizes biochemistry and an option in materials chemistry. The Biochemistry and Traditional Options are Graduation Composition and Communication certified by the American Chemical Society. A Bachelor of Arts degree program is Requirement hours (GCCR) .................................................................... 3 offered as well for students who want greater flexibility in the selection of courses to perhaps pursue more diverse degree options, including dual and double majors. For College Requirements all majors CHE 109 and CHE 110 have been defined as equivalent to CHE 105. The I. Foreign Language (placement exam recommended) ................................... 0-14 Department also offers the Master of Science and the Doctor of Philosophy degree. II. Disciplinary Requirements a. Natural Science (completed by Major Requirements) 128 hours b. Social Science ......................................................................................... 3 Any student earning a Bachelor of Science (BS)
    [Show full text]