DOCSLIB.ORG

Plaintext, Encryption, Ciphertext: a History of Cryptography and Its Influence on Contemporary Society

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Plaintext, Encryption, Ciphertext: a History of Cryptography and Its Influence on Contemporary Society TOC PLAINTEXT, ENCRYPTION, CIPHERTEXT: A HISTORY OF CRYPTOGRAPHY AND ITS INFLUENCE ON CONTEMPORARY SOCIETY QUINN DUPONT PHD DISSERTATION UNIVERSITY OF TORONTO, FACULTY OF INFORMATION CHAPTER 1 “REPRESENTATION” – SUBMISSION TO SIGCIS 2015 DRAFT (PLEASE DO NOT DISTRIBUTE) 1 TOC TABLE OF CONTENTS 1.! Introduction i.! Philological complexity ii.! What do we know of cryptography? iii.! Rewriting three schemata iv.! Chapter summaries Part One: Plaintext 2.! Representation i.! Alberti’s notation ii.! Mimesis and media iii.! Ancient theories of mimesis i.! Plato’s theory of mimesis ii.! Aristotle’s theory of mimesis iv.! Late medieval and renaissance web of resemblances v.! Conventia in memory techniques from Lull to Alberti’s cipher wheel vi.! Aemulatio, analogy, and sympathy in Trithemius’ magical cryptography 3.! Media and notation i.! Francis Bacon’s artifcial languages (1605-1623) i.! Francis Bacon’s bi-literal cipher ii.! Te development of notational schemes (1605-1686) iii.! Notational discourse networks i.! Identity and the alphabet ii.! A theory of notation 4.! Codes and codeworks i.! Agrippa (a book of the dead) i.! Forensic description of Agrippa ii.! Te compiled binary iii.! Te cryptographic algorithm 1.! Encryption efect 2.! Te “self-destruct” mechanism ii.! Bitcoin iii.! Executable software Part Two: Encryption 5.! Media of perception 6.! Communication and transmission 7.! Translation and Transcription 2 TOC Part Tree: Ciphertext 8.! Otherness and order, revealed 9.! Silence 10.! Epilogue i.! Politics: Homogeneity and visibility ii.! Rise of mnenotechnologies iii.! Ubiquitous cryptography 3 PART 1 – PLAINTEXT CHAPTER 2 – REPRESENTATION PLAINTEXT In his seminal work on cryptography De componendis cifris,1 Leon Battista Alberti (1404-1472) diverts from his task of exploring and inventing cryptography systems to recall a time strolling through a garden with his friend Dati. In the garden Alberti and Dati got to discussing Alberti’s desire to have his cryptog- raphy manual printed using the emerging “system of movable type” developed by “the German inventor [Gutenberg].”2 This convivial introduction to the invention of the polyalphabetic cipher might seem mis- placed—after all, the polyalphabetic cipher was a significant invention in its own right,3 and seemingly unrelated to print and typography. In fact, in Alberti’s entire corpus this is the only mention of the inven- tion of printing.4 Yet Alberti notes that it was such discussions with his friend that “brought us to similar appreciations… [of] strange characters with unusual meanings… called ciphers.”5 Rather than being a confused or mistaken association, this leap from movable type to ciphers is intended to signal deeper con- nections between writing, printing, and cryptography—the way that plaintext is articulated within a notational discourse network that ruptures ancient and medieval notions of representation and resem- blances by ushering in ideals of combinatory modularity and indexicality. Movable type was invented in Alberti’s lifetime and proved influential for him; Carpo calls Alberti the first “typographical architect.”6 For Alberti, the invention of movable type highlighted reproducible, mod- ular, indexical, and combinatory logics—logics inherent in the alphabet in the first place, but fully operationalized and made readily apparent in print. Alberti would put these logics to work in both his ar- chitectural and cryptographic theory. Alberti was familiar with the idea of reproducing identical copies from woodcuts, a pre-Gutenberg technique now called xylography.7 Xylography produced whole “images,” typically an etched image or vis- ual depiction. Xylography can even be used to reproduce a complete page (a “single-leaf” woodcut), including textual elements. Entire books—texts and images together—could be printed using xylographic processes, but this “block book” process was rare and may have even originated after Gutenberg’s inven- tion, as a quick and cheap alternative to movable type. In either configuration, image or text, producing duplicates from woodcuts was, once the original etch- ing is complete, a comparatively high-speed production technique. However, as Kittler notes, movable type presses were not designed to compete with the speed of xylography, instead they competed with the elegance of manuscript pages.8 And more to the point, printing from woodcuts, while possible, was rela- tively uncommon because each successive “edition” introduced the chance of error; this is a critical worry for technical works. The chance of copyist error was so high that authors typically wrote textual descrip- tions of what are fundamentally visual phenomena, such as architectural plans and forms (an “ekphrastic” 1 De componendis cifris was written in 1466 and remained in manuscript form during Alberti’s life. A modern Eng- lish translation by Kim William is available in Williams, March, and Wassell, The Mathematical Works of Leon Battista Alberti. References will be made to this edition, using modern page numbers and section divisions. The Latin version has been published in Meister, Die Geheimschrift Im Dienste Der Päpstlichen Kurie von Ihren Anfängen Bis Zum Ende Des XVI Jahrhunderts. 2 Alberti, “De Componendis Cifris,” 170 (ii). It seems Alberti was also aware of the work by Arnold Pannartz and Konrad Sweinheim, who introduced Roman typefaces; see March’s commentary, ibid., 189. March explains away this passage as an attempt to have his manuscript printed with the support of his patron or perhaps Pope Paul II. 3 Kahn, The Codebreakers. 4 Carpo, Architecture in the Age of Printing, 119. 5 Alberti, “De Componendis Cifris,” 170. 6 Carpo, The Alphabet and the Algorithm. 7 Carpo, Architecture in the Age of Printing. 8 Kittler, “The Perspective of Print.” 1 PART 1 – PLAINTEXT CHAPTER 2 – REPRESENTATION mode of expression), rather than employ pictorial techniques so susceptible to copying errors.9 Alberti was so worried of error that in his architectural works he stressed that copyists should write out numbers in longhand rather than using numeric symbols, even addressing the copyist directly in the work in several cases.10 Avoiding the introduction of errors was one of the principle advantages of alphabetic and typographic expression for the reproduction of technical works. Copyists could be counted on to (somewhat) reliably replicate the correct order of a determinate set of icons (the alphabet)—although even here, text rather than numeric symbols was the safer bet. Either way, copyists could not be counted on to replicate intricate pictorial content.11 To draw a technical image is to invite critical mistakes in the production of new man- uscripts or etchings. Carpo summarizes the reticence of those engaged in engineering and scientific communication: “The pretypographical architect knew that for… long-distance transmission, images were not a trustworthy medium. And he practiced his craft within these limitations.”12 Furthermore, the quattrocento era of Alberti is characterized by the expansion of economic, diplomatic, and scientific com- merce. Long-distance transmission of materials of many types became vitally important alongside the demands for secret diplomatic communication. To satisfy this need, Alberti argued, cryptography is needed—which has to be secret, capable of long distance transmission, and above all efficient (Alberti calls it “commodious” [scribetur commodius]).13 Error propagation is a real concern for cryptography. Alberti’s polyalphabetic encryption “mixes” multi- ple alphabets with plaintext that results in a kind of “diffuse” ciphertext. For any one letter of plaintext the corresponding ciphertext may be several letters, or mixed about in unnatural ways. The redundancy of natural languages permits transmission on noisy channels since redundant information accommodates er- rors. For cryptography, this redundancy is, ideally, deeply compromised. So-called “diffusion” and “confusion” techniques are basic methods available to cryptography, as they frustrate cryptanalytic tech- niques by “hiding” plaintext more deeply within a combinatory space.14 The result of highly diffuse ciphertext (what is typically understood as “good” cryptography) is that its transmission becomes very “brittle.” Even a small copying or transcription error may render much or all of the resulting ciphertext impossible to decrypt. Very careful transcription, or error-correction codes (as we use today) are a practi- cal necessity for cryptography.15 By the fifteenth century the introduction of type begun displacing the process of creating manuscripts by hand, which originally required the inscription of letters in situ (at the time of production). On a printed page letters pre-exist as units of type before the creation of words in which they occur. Roy Harris suggests that the “mechanical regularity of print confers upon each alphabetical symbol an independence and a constant visual identity which no earlier form of writing quite achieves.”16 In Alberti’s architectural work the letter became a metaphor for modularity, suggesting that the built form can be assembled just like a word created from its constitutive letters. The invention of the printing press transformed letters from icons in the imagination to manipulatable materials. Individual letters, in the form of literal pieces of metal, were quite obviously distinct from one another, yet each letter produced near-identical impressions with each use. One consequence of this 9 Carpo, Architecture in the Age of Printing,
Load more

Recommended publications
  • Classical Encryption Techniques
    CPE 542: CRYPTOGRAPHY & NETWORK SECURITY Chapter 2: Classical Encryption Techniques Dr. Lo’ai Tawalbeh Computer Engineering Department Jordan University of Science and Technology Jordan Dr. Lo’ai Tawalbeh Fall 2005 Introduction Basic Terminology • plaintext - the original message • ciphertext - the coded message • key - information used in encryption/decryption, and known only to sender/receiver • encipher (encrypt) - converting plaintext to ciphertext using key • decipher (decrypt) - recovering ciphertext from plaintext using key • cryptography - study of encryption principles/methods/designs • cryptanalysis (code breaking) - the study of principles/ methods of deciphering ciphertext Dr. Lo’ai Tawalbeh Fall 2005 1 Cryptographic Systems Cryptographic Systems are categorized according to: 1. The operation used in transferring plaintext to ciphertext: • Substitution: each element in the plaintext is mapped into another element • Transposition: the elements in the plaintext are re-arranged. 2. The number of keys used: • Symmetric (private- key) : both the sender and receiver use the same key • Asymmetric (public-key) : sender and receiver use different key 3. The way the plaintext is processed : • Block cipher : inputs are processed one block at a time, producing a corresponding output block. • Stream cipher: inputs are processed continuously, producing one element at a time (bit, Dr. Lo’ai Tawalbeh Fall 2005 Cryptographic Systems Symmetric Encryption Model Dr. Lo’ai Tawalbeh Fall 2005 2 Cryptographic Systems Requirements • two requirements for secure use of symmetric encryption: 1. a strong encryption algorithm 2. a secret key known only to sender / receiver •Y = Ek(X), where X: the plaintext, Y: the ciphertext •X = Dk(Y) • assume encryption algorithm is known •implies a secure channel to distribute key Dr.
    [Show full text]
  • COS433/Math 473: Cryptography Mark Zhandry Princeton University Spring 2017 Cryptography Is Everywhere a Long & Rich History
    COS433/Math 473: Cryptography Mark Zhandry Princeton University Spring 2017 Cryptography Is Everywhere A Long & Rich History Examples: • ~50 B.C. – Caesar Cipher • 1587 – Babington Plot • WWI – Zimmermann Telegram • WWII – Enigma • 1976/77 – Public Key Cryptography • 1990’s – Widespread adoption on the Internet Increasingly Important COS 433 Practice Theory Inherent to the study of crypto • Working knowledge of fundamentals is crucial • Cannot discern security by experimentation • Proofs, reductions, probability are necessary COS 433 What you should expect to learn: • Foundations and principles of modern cryptography • Core building blocks • Applications Bonus: • Debunking some Hollywood crypto • Better understanding of crypto news COS 433 What you will not learn: • Hacking • Crypto implementations • How to design secure systems • Viruses, worms, buffer overflows, etc Administrivia Course Information Instructor: Mark Zhandry (mzhandry@p) TA: Fermi Ma (fermima1@g) Lectures: MW 1:30-2:50pm Webpage: cs.princeton.edu/~mzhandry/2017-Spring-COS433/ Office Hours: please fill out Doodle poll Piazza piaZZa.com/princeton/spring2017/cos433mat473_s2017 Main channel of communication • Course announcements • Discuss homework problems with other students • Find study groups • Ask content questions to instructors, other students Prerequisites • Ability to read and write mathematical proofs • Familiarity with algorithms, analyZing running time, proving correctness, O notation • Basic probability (random variables, expectation) Helpful: • Familiarity with NP-Completeness, reductions • Basic number theory (modular arithmetic, etc) Reading No required text Computer Science/Mathematics Chapman & Hall/CRC If you want a text to follow along with: Second CRYPTOGRAPHY AND NETWORK SECURITY Cryptography is ubiquitous and plays a key role in ensuring data secrecy and Edition integrity as well as in securing computer systems more broadly.
    [Show full text]
  • The Mathemathics of Secrets.Pdf
    THE MATHEMATICS OF SECRETS THE MATHEMATICS OF SECRETS CRYPTOGRAPHY FROM CAESAR CIPHERS TO DIGITAL ENCRYPTION JOSHUA HOLDEN PRINCETON UNIVERSITY PRESS PRINCETON AND OXFORD Copyright c 2017 by Princeton University Press Published by Princeton University Press, 41 William Street, Princeton, New Jersey 08540 In the United Kingdom: Princeton University Press, 6 Oxford Street, Woodstock, Oxfordshire OX20 1TR press.princeton.edu Jacket image courtesy of Shutterstock; design by Lorraine Betz Doneker All Rights Reserved Library of Congress Cataloging-in-Publication Data Names: Holden, Joshua, 1970– author. Title: The mathematics of secrets : cryptography from Caesar ciphers to digital encryption / Joshua Holden. Description: Princeton : Princeton University Press, [2017] | Includes bibliographical references and index. Identifiers: LCCN 2016014840 | ISBN 9780691141756 (hardcover : alk. paper) Subjects: LCSH: Cryptography—Mathematics. | Ciphers. | Computer security. Classification: LCC Z103 .H664 2017 | DDC 005.8/2—dc23 LC record available at https://lccn.loc.gov/2016014840 British Library Cataloging-in-Publication Data is available This book has been composed in Linux Libertine Printed on acid-free paper. ∞ Printed in the United States of America 13579108642 To Lana and Richard for their love and support CONTENTS Preface xi Acknowledgments xiii Introduction to Ciphers and Substitution 1 1.1 Alice and Bob and Carl and Julius: Terminology and Caesar Cipher 1 1.2 The Key to the Matter: Generalizing the Caesar Cipher 4 1.3 Multiplicative Ciphers 6
    [Show full text]
  • An Archeology of Cryptography: Rewriting Plaintext, Encryption, and Ciphertext
    An Archeology of Cryptography: Rewriting Plaintext, Encryption, and Ciphertext By Isaac Quinn DuPont A thesis submitted in conformity with the requirements for the degree of Doctor of Philosophy Faculty of Information University of Toronto © Copyright by Isaac Quinn DuPont 2017 ii An Archeology of Cryptography: Rewriting Plaintext, Encryption, and Ciphertext Isaac Quinn DuPont Doctor of Philosophy Faculty of Information University of Toronto 2017 Abstract Tis dissertation is an archeological study of cryptography. It questions the validity of thinking about cryptography in familiar, instrumentalist terms, and instead reveals the ways that cryptography can been understood as writing, media, and computation. In this dissertation, I ofer a critique of the prevailing views of cryptography by tracing a number of long overlooked themes in its history, including the development of artifcial languages, machine translation, media, code, notation, silence, and order. Using an archeological method, I detail historical conditions of possibility and the technical a priori of cryptography. Te conditions of possibility are explored in three parts, where I rhetorically rewrite the conventional terms of art, namely, plaintext, encryption, and ciphertext. I argue that plaintext has historically been understood as kind of inscription or form of writing, and has been associated with the development of artifcial languages, and used to analyze and investigate the natural world. I argue that the technical a priori of plaintext, encryption, and ciphertext is constitutive of the syntactic iii and semantic properties detailed in Nelson Goodman’s theory of notation, as described in his Languages of Art. I argue that encryption (and its reverse, decryption) are deterministic modes of transcription, which have historically been thought of as the medium between plaintext and ciphertext.
    [Show full text]
  • Index-Of-Coincidence.Pdf
    The Index of Coincidence William F. Friedman in the 1930s developed the index of coincidence. For a given text X, where X is the sequence of letters x1x2…xn, the index of coincidence IC(X) is defined to be the probability that two randomly selected letters in the ciphertext represent, the same plaintext symbol. For a given ciphertext of length n, let n0, n1, …, n25 be the respective letter counts of A, B, C, . , Z in the ciphertext. Then, the index of coincidence can be computed as 25 ni (ni −1) IC = ∑ i=0 n(n −1) We can also calculate this index for any language source. For some source of letters, let p be the probability of occurrence of the letter a, p be the probability of occurrence of a € b the letter b, and so on. Then the index of coincidence for this source is 25 2 Isource = pa pa + pb pb +…+ pz pz = ∑ pi i=0 We can interpret the index of coincidence as the probability of randomly selecting two identical letters from the source. To see why the index of coincidence gives us useful information, first€ note that the empirical probability of randomly selecting two identical letters from a large English plaintext is approximately 0.065. This implies that an (English) ciphertext having an index of coincidence I of approximately 0.065 is probably associated with a mono-alphabetic substitution cipher, since this statistic will not change if the letters are simply relabeled (which is the effect of encrypting with a simple substitution). The longer and more random a Vigenere cipher keyword is, the more evenly the letters are distributed throughout the ciphertext.
    [Show full text]
  • Automating the Development of Chosen Ciphertext Attacks
    Automating the Development of Chosen Ciphertext Attacks Gabrielle Beck∗ Maximilian Zinkus∗ Matthew Green Johns Hopkins University Johns Hopkins University Johns Hopkins University [email protected] [email protected] [email protected] Abstract In this work we consider a specific class of vulner- ability: the continued use of unauthenticated symmet- In this work we investigate the problem of automating the ric encryption in many cryptographic systems. While development of adaptive chosen ciphertext attacks on sys- the research community has long noted the threat of tems that contain vulnerable format oracles. Unlike pre- adaptive-chosen ciphertext attacks on malleable en- vious attempts, which simply automate the execution of cryption schemes [17, 18, 56], these concerns gained known attacks, we consider a more challenging problem: practical salience with the discovery of padding ora- to programmatically derive a novel attack strategy, given cle attacks on a number of standard encryption pro- only a machine-readable description of the plaintext veri- tocols [6,7, 13, 22, 30, 40, 51, 52, 73]. Despite repeated fication function and the malleability characteristics of warnings to industry, variants of these attacks continue to the encryption scheme. We present a new set of algo- plague modern systems, including TLS 1.2’s CBC-mode rithms that use SAT and SMT solvers to reason deeply ciphersuite [5,7, 48] and hardware key management to- over the design of the system, producing an automated kens [10, 13]. A generalized variant, the format oracle attack strategy that can entirely decrypt protected mes- attack can be constructed when a decryption oracle leaks sages.
    [Show full text]
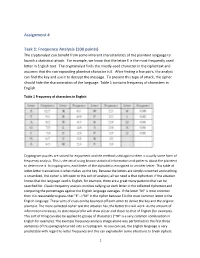
  • Assignment 4 Task 1: Frequency Analysis (100 Points)
    Assignment 4 Task 1: Frequency Analysis (100 points) The cryptanalyst can benefit from some inherent characteristics of the plaintext language to launch a statistical attack. For example, we know that the letter E is the most frequently used letter in English text. The cryptanalyst finds the mostly-used character in the ciphertext and assumes that the corresponding plaintext character is E. After finding a few pairs, the analyst can find the key and use it to decrypt the message. To prevent this type of attack, the cipher should hide the characteristics of the language. Table 1 contains frequency of characters in English. Table 1 Frequency of characters in English Cryptogram puzzles are solved for enjoyment and the method used against them is usually some form of frequency analysis. This is the act of using known statistical information and patterns about the plaintext to determine it. In cryptograms, each letter of the alphabet is encrypted to another letter. This table of letter-letter translations is what makes up the key. Because the letters are simply converted and nothing is scrambled, the cipher is left open to this sort of analysis; all we need is that ciphertext. If the attacker knows that the language used is English, for example, there are a great many patterns that can be searched for. Classic frequency analysis involves tallying up each letter in the collected ciphertext and comparing the percentages against the English language averages. If the letter "M" is most common then it is reasonable to guess that "E"-->"M" in the cipher because E is the most common letter in the English language.
    [Show full text]
  • Chap 2. Basic Encryption and Decryption
    Chap 2. Basic Encryption and Decryption H. Lee Kwang Department of Electrical Engineering & Computer Science, KAIST Objectives • Concepts of encryption • Cryptanalysis: how encryption systems are “broken” 2.1 Terminology and Background • Notations – S: sender – R: receiver – T: transmission medium – O: outsider, interceptor, intruder, attacker, or, adversary • S wants to send a message to R – S entrusts the message to T who will deliver it to R – Possible actions of O • block(interrupt), intercept, modify, fabricate • Chapter 1 2.1.1 Terminology • Encryption and Decryption – encryption: a process of encoding a message so that its meaning is not obvious – decryption: the reverse process • encode(encipher) vs. decode(decipher) – encoding: the process of translating entire words or phrases to other words or phrases – enciphering: translating letters or symbols individually – encryption: the group term that covers both encoding and enciphering 2.1.1 Terminology • Plaintext vs. Ciphertext – P(plaintext): the original form of a message – C(ciphertext): the encrypted form • Basic operations – plaintext to ciphertext: encryption: C = E(P) – ciphertext to plaintext: decryption: P = D(C) – requirement: P = D(E(P)) 2.1.1 Terminology • Encryption with key If the encryption algorithm should fall into the interceptor’s – encryption key: KE – decryption key: K hands, future messages can still D be kept secret because the – C = E(K , P) E interceptor will not know the – P = D(KD, E(KE, P)) key value • Keyless Cipher – a cipher that does not require the
    [Show full text]
  • Shift Cipher Substitution Cipher Vigenère Cipher Hill Cipher
    Lecture 2 Classical Cryptosystems Shift cipher Substitution cipher Vigenère cipher Hill cipher 1 Shift Cipher • A Substitution Cipher • The Key Space: – [0 … 25] • Encryption given a key K: – each letter in the plaintext P is replaced with the K’th letter following the corresponding number ( shift right ) • Decryption given K: – shift left • History: K = 3, Caesar’s cipher 2 Shift Cipher • Formally: • Let P=C= K=Z 26 For 0≤K≤25 ek(x) = x+K mod 26 and dk(y) = y-K mod 26 ʚͬ, ͭ ∈ ͔ͦͪ ʛ 3 Shift Cipher: An Example ABCDEFGHIJKLMNOPQRSTUVWXYZ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 • P = CRYPTOGRAPHYISFUN Note that punctuation is often • K = 11 eliminated • C = NCJAVZRCLASJTDQFY • C → 2; 2+11 mod 26 = 13 → N • R → 17; 17+11 mod 26 = 2 → C • … • N → 13; 13+11 mod 26 = 24 → Y 4 Shift Cipher: Cryptanalysis • Can an attacker find K? – YES: exhaustive search, key space is small (<= 26 possible keys). – Once K is found, very easy to decrypt Exercise 1: decrypt the following ciphertext hphtwwxppelextoytrse Exercise 2: decrypt the following ciphertext jbcrclqrwcrvnbjenbwrwn VERY useful MATLAB functions can be found here: http://www2.math.umd.edu/~lcw/MatlabCode/ 5 General Mono-alphabetical Substitution Cipher • The key space: all possible permutations of Σ = {A, B, C, …, Z} • Encryption, given a key (permutation) π: – each letter X in the plaintext P is replaced with π(X) • Decryption, given a key π: – each letter Y in the ciphertext C is replaced with π-1(Y) • Example ABCDEFGHIJKLMNOPQRSTUVWXYZ πBADCZHWYGOQXSVTRNMSKJI PEFU • BECAUSE AZDBJSZ 6 Strength of the General Substitution Cipher • Exhaustive search is now infeasible – key space size is 26! ≈ 4*10 26 • Dominates the art of secret writing throughout the first millennium A.D.
    [Show full text]
  • I Islander Readers I Say the Damdest I Things... 7A ARTS » LEISURE: Life's
    mm ARTS » LEISURE: EVERY WEEK: i Islander readers Life's a beach 1B Calendar 27A I say the damdest Ostrich eggs, . Classifieds 18C i things... 7A anyone? 4B Island map 25A 1961-1986 Still first after 25 years VOL. 26, NO. 13 TUESDAY, MARCH 3>, 1987 THREE SECTIONS, 76 PAGES 50 CENTS Who's the wiser? Michael Welngart, staff member at Care and ed howl back in Its nest on Captiva last weekend. The strong winds last week. Story on page 1C. Photo by Rehabilitation of Wildlife, placed this baby great horn- owl was one of two that was blown from the nest by Rlcki Kosakow Cooper. INDEX2 •-,•.•. ALSO THIS WEEK How do you Executive women Westall isn't discouraged Arts-Leisure 4B organize new chapter when osprey parents Brldae 13B combine computers Club news 14B with seashells? of service club on Sanibel vent their indignation Fishing tips 10C Long-time Island, shellers President Kappy King Cole in- In his first osprey chick banding Nature programs 3C Margaret Thorsen and Ede vites interested Island business expedition of the season, Mark Obituary 15A Mugridge have found a way - and women to learn more about the "Bird" Westall suffered minor in- juries to his arm when an angry Police beat 4A their efforts will benefit the Sanibel fledgling Sanibel-Captiva Zonta Club. osprey mother dove at him. Shelling tips 11C Shell Museum and Research Foundation. 23B 10A The ISLANDER Tuesday, March 31, 1987 3A City hopes to gain endorsement of Realtors Tuesday for sales tax to help purchase sensitive wetlands 2A Island Shorts March 31,1987 By BARBARA BRUNDAGE directors, as do city councilmen, view a recreational facilities would not be inherent obligation and responsibility Islander staff writer real estate transaction tax as the most included.
    [Show full text]
  • Can You Keep a Secret?
    Codes and Ciphers 20 Can You Keep a Secret? Codes and ciphers have been around just about as long as there has been written language. The ability to communicate in secret – as well as the ability to peer into the secret communications of others – has been central to a surprising number of major world events throughout history, often with nations as well as lives hanging in the balance. A word first about the difference between a code and a cipher: • A code is a secret language used to disguise the meaning of a message. The simplest form is a “jargon code,” where a particular phrase corresponds to a previously defined message. “The milkman comes in the morning,” for example, could mean “the invasion begins at dawn.” • A cipher conceals what is referred to as a “plaintext” message by substituting (a “substitu- tion cipher”) and/or scrambling (a “transposition cipher”) the letters. As we shall see later, a simple substitution cipher may encrypt the message “Call me tomorrow morning” as “FDO OPH WRP RUU RZP RUQ LQJ.” For our purposes, we will use such general terms as “code,” Cryptography, sometimes called “cryptology,” is “code breaker,” “encryp- tion” and “decryption” to from the Greek, meaning “hidden writing,” and its refer both to codes and ci- use has been documented for over 2,000 years. phers, rather than repeatedly drawing the distinction between the two. Hidden Writing Cryptography, sometimes called “cryptology,” is from the Greek, meaning “hidden writing” and its use has been documented for over 2,000 years. From the beginning, codes have always been of greatest use in matters of war and diplomacy.
    [Show full text]
  • Substitution Ciphers
    Foundations of Computer Security Lecture 40: Substitution Ciphers Dr. Bill Young Department of Computer Sciences University of Texas at Austin Lecture 40: 1 Substitution Ciphers Substitution Ciphers A substitution cipher is one in which each symbol of the plaintext is exchanged for another symbol. If this is done uniformly this is called a monoalphabetic cipher or simple substitution cipher. If different substitutions are made depending on where in the plaintext the symbol occurs, this is called a polyalphabetic substitution. Lecture 40: 2 Substitution Ciphers Simple Substitution A simple substitution cipher is an injection (1-1 mapping) of the alphabet into itself or another alphabet. What is the key? A simple substitution is breakable; we could try all k! mappings from the plaintext to ciphertext alphabets. That’s usually not necessary. Redundancies in the plaintext (letter frequencies, digrams, etc.) are reflected in the ciphertext. Not all substitution ciphers are simple substitution ciphers. Lecture 40: 3 Substitution Ciphers Caesar Cipher The Caesar Cipher is a monoalphabetic cipher in which each letter is replaced in the encryption by another letter a fixed “distance” away in the alphabet. For example, A is replaced by C, B by D, ..., Y by A, Z by B, etc. What is the key? What is the size of the keyspace? Is the algorithm strong? Lecture 40: 4 Substitution Ciphers Vigen`ere Cipher The Vigen`ere Cipher is an example of a polyalphabetic cipher, sometimes called a running key cipher because the key is another text. Start with a key string: “monitors to go to the bathroom” and a plaintext to encrypt: “four score and seven years ago.” Align the two texts, possibly removing spaces: plaintext: fours corea ndsev enyea rsago key: monit orsto gotot hebat hroom ciphertext: rcizl qfkxo trlso lrzet yjoua Then use the letter pairs to look up an encryption in a table (called a Vigen`ere Tableau or tabula recta).
    [Show full text]