DOCSLIB.ORG

Cryptanalysis of the ``Kindle'' Cipher

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Cryptanalysis of the ``Kindle'' Cipher Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . Cryptanalysis of the “Kindle” Cipher Alex Biryukov, Gaëtan Leurent, Arnab Roy University of Luxembourg SAC 2012 A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 1 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . Cryptography: theory and practice In theory In practice ▶ Random Oracle ▶ Algorithms ▶ ▶ Ideal Cipher AES ▶ SHA2 ▶ Perfect source of ▶ RSA randomness ▶ Modes of operation ▶ CBC ▶ OAEP ▶ ... ▶ . Random Number Generators ▶ Hardware RNG ▶ PRNG A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 2 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . Cryptography in the real world Several examples of flaws in industrial cryptography: ▶ Bad random source ▶ SLL with 16bit entropy (Debian) ▶ ECDSA with fixed k (Sony) ▶ Bad key size ▶ RSA512 (TI) ▶ Export restrictions... ▶ Bad mode of operation ▶ CBCMAC with the RC4 streamcipher (Microsoft) ▶ TEA with DaviesMeyer (Microsoft) ▶ Bad (proprietary) algorithm ▶ A5/1 (GSM) ▶ CSS (DVD forum) ▶ Crypto1 (MIFARE/NXP) ▶ KeeLoq (Microchip) A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 3 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . Amazon Kindle ▶ Ebook reader by Amazon ▶ Most popular ebook reader (≈ 50% share) ▶ 4 generations, 7 devices ▶ Software reader for 7 OS, plus cloud reader ▶ Several million devices sold ▶ Amazon sells more ebooks than paper books ▶ Uses crypto for DRM (Digital Rights Management) A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 4 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . Digital Rights Management ▶ Company sells media (music, video, ebook, game, ...) ▶ Wants to prevent sharing . ▶ Customer should read but not copy Charly DRM scheme ▶ Encipher media ▶ Bob Give player to users ▶ Hardware or software Alice ▶ Player contains the key A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 5 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . Digital Rights Management ▶ Company sells media (music, video, ebook, game, ...) ▶ Wants to prevent sharing . ▶ Customer should read but not copy Charly DRM scheme ▶ Encipher media ▶ ? Bob Give player to users ▶ Hardware or software Alice ▶ Player contains the key A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 5 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . Breaking DRM ▶ Copy the media while being played . ▶ Extract the key from the player, decipher media . Tamperproof hardware? Obfuscation? Whitebox crypto? ▶ No need to break the crypto! ▶ Pirates break once, copy... A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 6 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . Digital Rights Management Legal User ▶ Can only use authorized player ▶ Collection lockedin . ▶ DRM can restrict user rights ▶ Lending, reselling, ... Charly ▶ No format shifting: ▶ play DVD on tablet ▶ read ebook w/ speech synth. Bob Illegal User Alice ▶ Can still find illegal copies ▶ Can do anything with the media A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 7 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . DRM on the Kindle ▶ Kindle ebooks use DRM ▶ Like any DRM system, it is bound to fail ▶ In practice, it is easy to extract the key (Google for details...) Overview ▶ In this talk, we study the cipher used in this DRM system We don’t study the DRM system itself ▶ The DRM system uses a cipher called PC1 ▶ It’s a really weak cipher... A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 8 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . Outline Introduction Cryptography in the real world Digital Rights Management The PC1 Cipher Description Weaknesses Known-plaintext key-recovery Collision detection Key recovery Ciphertext only key-recovery Bias with independent keys Recovering the plaintext A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 9 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . The PC1 Cipher ▶ Designed by Pukall in 1991 ▶ Posted on Usenet p π s 8 ▶ Kindle DRM based on PC1 8 16 ▶ Selfsynchronizing stream cipher No IV! w . ▶ k 128 햪향 8 × 16 햲향 16bit arithmetic: add, mult, xor Main loop (햪향 and 햲향) σk σs 16 16 for 0 ≤ i < 8 do 16 w ← w ⊕ ki ⊕ (π × 257) 햿허헅햽 x ← 346 × w 8 σ w ← 20021 × w + 1 p c s ← s + x σ ← σ ⊕ w ⊕ s s ← 20021 × (s + (i+1 mod 8)) + x A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 10 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . Weakness 1: T-functions Weakness This is a Tfunction p π s 8 ▶ Low bits of the output 8 16 depend only on the low bits of the input . w ▶ Add, mult, xor k 8 × 16 햪향 8 × 16 햲향 ▶ Guess 8 × 9 bits of the key σk σs 16 16 ▶ Get 9 bits before the fold 16 ▶ Get 1 bit after the fold 햿허헅햽 ▶ Verify with known plaintext 8 σ p c ▶ Complexity: 272 some bytes of known plaintext A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 11 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . Weakness 2: small state Weakness The state is very small p π s 8 s 16bit 8 16 π 8bit, keyindependent . w k 8 × 16 햪향 8 × 16 햲향 ▶ Build a set of plaintexts xi‖y, xi’s with fixed xorsum σk σs ▶ With high probability the 16 16 16 state collides after xi and xj 햿허헅햽 ▶ Same encryption of y 8 σ p c ▶ Complexity: 28 CP (distinguisher) A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 12 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . Outline Introduction Cryptography in the real world Digital Rights Management The PC1 Cipher Description Weaknesses Known-plaintext key-recovery Collision detection Key recovery Ciphertext only key-recovery Bias with independent keys Recovering the plaintext A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 13 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . Collision detection Can we use state collisions in a knownplaintext attack? How much wood could a woodchuck chuck gfecuhaupmaqcdlvtognfgdhisqghugbrfqvc if a woodchuck could chuck wood? ghxadiaphjjxicwpidkasqghugbqsjbf ▶ In a natural language text, some words will be repeated. ▶ With some probability (p ≈ 2−24), two instances of a repeated word begin with the same state. ▶ This gives a repetition in the ciphertext. ▶ When we detect a repetition in the plaintext and ciphertext, we can assume that the state is colliding. A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 14 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . Collision detection Can we use state collisions in a knownplaintext attack? How much wood could a woodchuck chuck gfecuhaupmaqcdlvtognfgdhisqghugbrfqvc if a woodchuck could chuck wood? ghxadiaphjjxicwpidkasqghugbqsjbf ▶ In a natural language text, some words will be repeated. ▶ With some probability (p ≈ 2−24), two instances of a repeated word begin with the same state. ▶ This gives a repetition in the ciphertext. ▶ When we detect a repetition in the plaintext and ciphertext, we can assume that the state is colliding. A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 14 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . Collision detection Can we use state collisions in a knownplaintext attack? How much wood could a woodchuck chuck gfecuhaupmaqcdlvtognfgdhisqghugbrfqvc if a woodchuck could chuck wood? ghxadiaphjjxicwpidkasqghugbqsjbf ▶ In a natural language text, some words will be repeated. ▶ With some probability (p ≈ 2−24), two instances of a repeated word begin with the same state. ▶ This gives a repetition in the ciphertext. ▶ When we detect a repetition in the plaintext and ciphertext, we can assume that the state is colliding. A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 14 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . Collision detection Can we use state collisions in a knownplaintext attack? How much wood could a woodchuck chuck gfecuhaupmaqcdlvtognfgdhisqghugbrfqvc if a woodchuck could chuck wood? ghxadiaphjjxicwpidkasqghugbqsjbf ▶ In a natural language text, some words will be repeated. ▶ With some probability (p ≈ 2−24), two instances of a repeated word begin with the same state. ▶ This gives a repetition in the ciphertext. ▶ When we detect a repetition in the plaintext and ciphertext, we can assume that the state is colliding. A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 14 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . Collision Based Key-recovery p π s ▶ Use state collisions to 8 8 16 test key guess ▶ Skip output part . w k 8 × 16 햪향 8 × 16 햲향 Weakness This is a Tfunction σk σs ▶ 16 16 Guess 8 × 1 bits of the key 16 ▶ Compute 1 bit of s, 햿허헅햽 check collisions in s 8 σ ▶ Repeat with 2nd bit, ... p c A. Biryukov, G. Leurent, A. Roy (uni.lu) Cryptanalysis of the “Kindle” Cipher SAC 2012 15 / 22 Introduction PC1 Known-plaintext key-recovery Ciphertext only key-recovery Conclusion . Collision Based Key-recovery p π s ▶ Use state collisions to 8 8 16 test key guess ▶ Skip output part .
Load more

Recommended publications
  • Improved Cryptanalysis of the Reduced Grøstl Compression Function, ECHO Permutation and AES Block Cipher
    Improved Cryptanalysis of the Reduced Grøstl Compression Function, ECHO Permutation and AES Block Cipher Florian Mendel1, Thomas Peyrin2, Christian Rechberger1, and Martin Schl¨affer1 1 IAIK, Graz University of Technology, Austria 2 Ingenico, France [email protected],[email protected] Abstract. In this paper, we propose two new ways to mount attacks on the SHA-3 candidates Grøstl, and ECHO, and apply these attacks also to the AES. Our results improve upon and extend the rebound attack. Using the new techniques, we are able to extend the number of rounds in which available degrees of freedom can be used. As a result, we present the first attack on 7 rounds for the Grøstl-256 output transformation3 and improve the semi-free-start collision attack on 6 rounds. Further, we present an improved known-key distinguisher for 7 rounds of the AES block cipher and the internal permutation used in ECHO. Keywords: hash function, block cipher, cryptanalysis, semi-free-start collision, known-key distinguisher 1 Introduction Recently, a new wave of hash function proposals appeared, following a call for submissions to the SHA-3 contest organized by NIST [26]. In order to analyze these proposals, the toolbox which is at the cryptanalysts' disposal needs to be extended. Meet-in-the-middle and differential attacks are commonly used. A recent extension of differential cryptanalysis to hash functions is the rebound attack [22] originally applied to reduced (7.5 rounds) Whirlpool (standardized since 2000 by ISO/IEC 10118-3:2004) and a reduced version (6 rounds) of the SHA-3 candidate Grøstl-256 [14], which both have 10 rounds in total.
    [Show full text]
  • Key-Dependent Approximations in Cryptanalysis. an Application of Multiple Z4 and Non-Linear Approximations
    KEY-DEPENDENT APPROXIMATIONS IN CRYPTANALYSIS. AN APPLICATION OF MULTIPLE Z4 AND NON-LINEAR APPROXIMATIONS. FX Standaert, G Rouvroy, G Piret, JJ Quisquater, JD Legat Universite Catholique de Louvain, UCL Crypto Group, Place du Levant, 3, 1348 Louvain-la-Neuve, standaert,rouvroy,piret,quisquater,[email protected] Linear cryptanalysis is a powerful cryptanalytic technique that makes use of a linear approximation over some rounds of a cipher, combined with one (or two) round(s) of key guess. This key guess is usually performed by a partial decryp- tion over every possible key. In this paper, we investigate a particular class of non-linear boolean functions that allows to mount key-dependent approximations of s-boxes. Replacing the classical key guess by these key-dependent approxima- tions allows to quickly distinguish a set of keys including the correct one. By combining different relations, we can make up a system of equations whose solu- tion is the correct key. The resulting attack allows larger flexibility and improves the success rate in some contexts. We apply it to the block cipher Q. In parallel, we propose a chosen-plaintext attack against Q that reduces the required number of plaintext-ciphertext pairs from 297 to 287. 1. INTRODUCTION In its basic version, linear cryptanalysis is a known-plaintext attack that uses a linear relation between input-bits, output-bits and key-bits of an encryption algorithm that holds with a certain probability. If enough plaintext-ciphertext pairs are provided, this approximation can be used to assign probabilities to the possible keys and to locate the most probable one.
    [Show full text]
  • Classical Encryption Techniques
    CPE 542: CRYPTOGRAPHY & NETWORK SECURITY Chapter 2: Classical Encryption Techniques Dr. Lo’ai Tawalbeh Computer Engineering Department Jordan University of Science and Technology Jordan Dr. Lo’ai Tawalbeh Fall 2005 Introduction Basic Terminology • plaintext - the original message • ciphertext - the coded message • key - information used in encryption/decryption, and known only to sender/receiver • encipher (encrypt) - converting plaintext to ciphertext using key • decipher (decrypt) - recovering ciphertext from plaintext using key • cryptography - study of encryption principles/methods/designs • cryptanalysis (code breaking) - the study of principles/ methods of deciphering ciphertext Dr. Lo’ai Tawalbeh Fall 2005 1 Cryptographic Systems Cryptographic Systems are categorized according to: 1. The operation used in transferring plaintext to ciphertext: • Substitution: each element in the plaintext is mapped into another element • Transposition: the elements in the plaintext are re-arranged. 2. The number of keys used: • Symmetric (private- key) : both the sender and receiver use the same key • Asymmetric (public-key) : sender and receiver use different key 3. The way the plaintext is processed : • Block cipher : inputs are processed one block at a time, producing a corresponding output block. • Stream cipher: inputs are processed continuously, producing one element at a time (bit, Dr. Lo’ai Tawalbeh Fall 2005 Cryptographic Systems Symmetric Encryption Model Dr. Lo’ai Tawalbeh Fall 2005 2 Cryptographic Systems Requirements • two requirements for secure use of symmetric encryption: 1. a strong encryption algorithm 2. a secret key known only to sender / receiver •Y = Ek(X), where X: the plaintext, Y: the ciphertext •X = Dk(Y) • assume encryption algorithm is known •implies a secure channel to distribute key Dr.
    [Show full text]
  • Related-Key Cryptanalysis of 3-WAY, Biham-DES,CAST, DES-X, Newdes, RC2, and TEA
    Related-Key Cryptanalysis of 3-WAY, Biham-DES,CAST, DES-X, NewDES, RC2, and TEA John Kelsey Bruce Schneier David Wagner Counterpane Systems U.C. Berkeley kelsey,schneier @counterpane.com [email protected] f g Abstract. We present new related-key attacks on the block ciphers 3- WAY, Biham-DES, CAST, DES-X, NewDES, RC2, and TEA. Differen- tial related-key attacks allow both keys and plaintexts to be chosen with specific differences [KSW96]. Our attacks build on the original work, showing how to adapt the general attack to deal with the difficulties of the individual algorithms. We also give specific design principles to protect against these attacks. 1 Introduction Related-key cryptanalysis assumes that the attacker learns the encryption of certain plaintexts not only under the original (unknown) key K, but also under some derived keys K0 = f(K). In a chosen-related-key attack, the attacker specifies how the key is to be changed; known-related-key attacks are those where the key difference is known, but cannot be chosen by the attacker. We emphasize that the attacker knows or chooses the relationship between keys, not the actual key values. These techniques have been developed in [Knu93b, Bih94, KSW96]. Related-key cryptanalysis is a practical attack on key-exchange protocols that do not guarantee key-integrity|an attacker may be able to flip bits in the key without knowing the key|and key-update protocols that update keys using a known function: e.g., K, K + 1, K + 2, etc. Related-key attacks were also used against rotor machines: operators sometimes set rotors incorrectly.
    [Show full text]
  • Impossible Differential Cryptanalysis of TEA, XTEA and HIGHT
    Preliminaries Impossible Differential Attacks on TEA and XTEA Impossible Differential Cryptanalysis of HIGHT Conclusion Impossible Differential Cryptanalysis of TEA, XTEA and HIGHT Jiazhe Chen1;2 Meiqin Wang1;2 Bart Preneel2 1Shangdong University, China 2KU Leuven, ESAT/COSIC and IBBT, Belgium AfricaCrypt 2012 July 10, 2012 1 / 27 Preliminaries Impossible Differential Attacks on TEA and XTEA Impossible Differential Cryptanalysis of HIGHT Conclusion Preliminaries Impossible Differential Attack TEA, XTEA and HIGHT Impossible Differential Attacks on TEA and XTEA Deriving Impossible Differentials for TEA and XTEA Key Recovery Attacks on TEA and XTEA Impossible Differential Cryptanalysis of HIGHT Impossible Differential Attacks on HIGHT Conclusion 2 / 27 I Pr(∆A ! ∆B) = 1, Pr(∆G ! ∆F) = 1, ∆B 6= ∆F, Pr(∆A ! ∆G) = 0 I Extend the impossible differential forward and backward to attack a block cipher I Guess subkeys in Part I and Part II, if there is a pair meets ∆A and ∆G, then the subkey guess must be wrong P I A B F G II C Preliminaries Impossible Differential Attacks on TEA and XTEA Impossible Differential Cryptanalysis of HIGHT Conclusion Impossible Differential Attack Impossible Differential Attack 3 / 27 I Pr(∆A ! ∆B) = 1, Pr(∆G ! ∆F) = 1, ∆B 6= ∆F, Pr(∆A ! ∆G) = 0 I Extend the impossible differential forward and backward to attack a block cipher I Guess subkeys in Part I and Part II, if there is a pair meets ∆A and ∆G, then the subkey guess must be wrong P I A B F G II C Preliminaries Impossible Differential Attacks on TEA and XTEA Impossible
    [Show full text]
  • Recommendation for Block Cipher Modes of Operation Methods
    NIST Special Publication 800-38A Recommendation for Block 2001 Edition Cipher Modes of Operation Methods and Techniques Morris Dworkin C O M P U T E R S E C U R I T Y ii C O M P U T E R S E C U R I T Y Computer Security Division Information Technology Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899-8930 December 2001 U.S. Department of Commerce Donald L. Evans, Secretary Technology Administration Phillip J. Bond, Under Secretary of Commerce for Technology National Institute of Standards and Technology Arden L. Bement, Jr., Director iii Reports on Information Security Technology The Information Technology Laboratory (ITL) at the National Institute of Standards and Technology (NIST) promotes the U.S. economy and public welfare by providing technical leadership for the Nation’s measurement and standards infrastructure. ITL develops tests, test methods, reference data, proof of concept implementations, and technical analyses to advance the development and productive use of information technology. ITL’s responsibilities include the development of technical, physical, administrative, and management standards and guidelines for the cost-effective security and privacy of sensitive unclassified information in Federal computer systems. This Special Publication 800-series reports on ITL’s research, guidance, and outreach efforts in computer security, and its collaborative activities with industry, government, and academic organizations. Certain commercial entities, equipment, or materials may be identified in this document in order to describe an experimental procedure or concept adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the entities, materials, or equipment are necessarily the best available for the purpose.
    [Show full text]
  • Polish Mathematicians Finding Patterns in Enigma Messages
    Fall 2006 Chris Christensen MAT/CSC 483 Machine Ciphers Polyalphabetic ciphers are good ways to destroy the usefulness of frequency analysis. Implementation can be a problem, however. The key to a polyalphabetic cipher specifies the order of the ciphers that will be used during encryption. Ideally there would be as many ciphers as there are letters in the plaintext message and the ordering of the ciphers would be random – an one-time pad. More commonly, some rotation among a small number of ciphers is prescribed. But, rotating among a small number of ciphers leads to a period, which a cryptanalyst can exploit. Rotating among a “large” number of ciphers might work, but that is hard to do by hand – there is a high probability of encryption errors. Maybe, a machine. During World War II, all the Allied and Axis countries used machine ciphers. The United States had SIGABA, Britain had TypeX, Japan had “Purple,” and Germany (and Italy) had Enigma. SIGABA http://en.wikipedia.org/wiki/SIGABA 1 A TypeX machine at Bletchley Park. 2 From the 1920s until the 1970s, cryptology was dominated by machine ciphers. What the machine ciphers typically did was provide a mechanical way to rotate among a large number of ciphers. The rotation was not random, but the large number of ciphers that were available could prevent depth from occurring within messages and (if the machines were used properly) among messages. We will examine Enigma, which was broken by Polish mathematicians in the 1930s and by the British during World War II. The Japanese Purple machine, which was used to transmit diplomatic messages, was broken by William Friedman’s cryptanalysts.
    [Show full text]
  • Partly-Pseudo-Linear Cryptanalysis of Reduced-Round SPECK
    cryptography Article Partly-Pseudo-Linear Cryptanalysis of Reduced-Round SPECK Sarah A. Alzakari * and Poorvi L. Vora Department of Computer Science, The George Washington University, 800 22nd St. NW, Washington, DC 20052, USA; [email protected] * Correspondence: [email protected] Abstract: We apply McKay’s pseudo-linear approximation of addition modular 2n to lightweight ARX block ciphers with large words, specifically the SPECK family. We demonstrate that a pseudo- linear approximation can be combined with a linear approximation using the meet-in-the-middle attack technique to recover several key bits. Thus we illustrate improvements to SPECK linear distinguishers based solely on Cho–Pieprzyk approximations by combining them with pseudo-linear approximations, and propose key recovery attacks. Keywords: SPECK; pseudo-linear cryptanalysis; linear cryptanalysis; partly-pseudo-linear attack 1. Introduction ARX block ciphers—which rely on Addition-Rotation-XOR operations performed a number of times—provide a common approach to lightweight cipher design. In June 2013, a group of inventors from the US’s National Security Agency (NSA) proposed two families of lightweight block ciphers, SIMON and SPECK—each of which comes in a variety of widths and key sizes. The SPECK cipher, as an ARX cipher, provides efficient software implementations, while SIMON provides efficient hardware implementations. Moreover, both families perform well in both hardware and software and offer the flexibility across Citation: Alzakari, S.; Vora, P. different platforms that will be required by future applications [1,2]. In this paper, we focus Partly-Pseudo-Linear Cryptanalysis on the SPECK family as an example lightweight ARX block cipher to illustrate our attack.
    [Show full text]
  • Index-Of-Coincidence.Pdf
    The Index of Coincidence William F. Friedman in the 1930s developed the index of coincidence. For a given text X, where X is the sequence of letters x1x2…xn, the index of coincidence IC(X) is defined to be the probability that two randomly selected letters in the ciphertext represent, the same plaintext symbol. For a given ciphertext of length n, let n0, n1, …, n25 be the respective letter counts of A, B, C, . , Z in the ciphertext. Then, the index of coincidence can be computed as 25 ni (ni −1) IC = ∑ i=0 n(n −1) We can also calculate this index for any language source. For some source of letters, let p be the probability of occurrence of the letter a, p be the probability of occurrence of a € b the letter b, and so on. Then the index of coincidence for this source is 25 2 Isource = pa pa + pb pb +…+ pz pz = ∑ pi i=0 We can interpret the index of coincidence as the probability of randomly selecting two identical letters from the source. To see why the index of coincidence gives us useful information, first€ note that the empirical probability of randomly selecting two identical letters from a large English plaintext is approximately 0.065. This implies that an (English) ciphertext having an index of coincidence I of approximately 0.065 is probably associated with a mono-alphabetic substitution cipher, since this statistic will not change if the letters are simply relabeled (which is the effect of encrypting with a simple substitution). The longer and more random a Vigenere cipher keyword is, the more evenly the letters are distributed throughout the ciphertext.
    [Show full text]
  • Automating the Development of Chosen Ciphertext Attacks
    Automating the Development of Chosen Ciphertext Attacks Gabrielle Beck∗ Maximilian Zinkus∗ Matthew Green Johns Hopkins University Johns Hopkins University Johns Hopkins University [email protected] [email protected] [email protected] Abstract In this work we consider a specific class of vulner- ability: the continued use of unauthenticated symmet- In this work we investigate the problem of automating the ric encryption in many cryptographic systems. While development of adaptive chosen ciphertext attacks on sys- the research community has long noted the threat of tems that contain vulnerable format oracles. Unlike pre- adaptive-chosen ciphertext attacks on malleable en- vious attempts, which simply automate the execution of cryption schemes [17, 18, 56], these concerns gained known attacks, we consider a more challenging problem: practical salience with the discovery of padding ora- to programmatically derive a novel attack strategy, given cle attacks on a number of standard encryption pro- only a machine-readable description of the plaintext veri- tocols [6,7, 13, 22, 30, 40, 51, 52, 73]. Despite repeated fication function and the malleability characteristics of warnings to industry, variants of these attacks continue to the encryption scheme. We present a new set of algo- plague modern systems, including TLS 1.2’s CBC-mode rithms that use SAT and SMT solvers to reason deeply ciphersuite [5,7, 48] and hardware key management to- over the design of the system, producing an automated kens [10, 13]. A generalized variant, the format oracle attack strategy that can entirely decrypt protected mes- attack can be constructed when a decryption oracle leaks sages.
    [Show full text]
  • Secure Communications One Time Pad Cipher
    Cipher Machines & Cryptology © 2010 – D. Rijmenants http://users.telenet.be/d.rijmenants THE COMPLETE GUIDE TO SECURE COMMUNICATIONS WITH THE ONE TIME PAD CIPHER DIRK RIJMENANTS Abstract : This paper provides standard instructions on how to protect short text messages with one-time pad encryption. The encryption is performed with nothing more than a pencil and paper, but provides absolute message security. If properly applied, it is mathematically impossible for any eavesdropper to decrypt or break the message without the proper key. Keywords : cryptography, one-time pad, encryption, message security, conversion table, steganography, codebook, message verification code, covert communications, Jargon code, Morse cut numbers. version 012-2011 1 Contents Section Page I. Introduction 2 II. The One-time Pad 3 III. Message Preparation 4 IV. Encryption 5 V. Decryption 6 VI. The Optional Codebook 7 VII. Security Rules and Advice 8 VIII. Appendices 17 I. Introduction One-time pad encryption is a basic yet solid method to protect short text messages. This paper explains how to use one-time pads, how to set up secure one-time pad communications and how to deal with its various security issues. It is easy to learn to work with one-time pads, the system is transparent, and you do not need special equipment or any knowledge about cryptographic techniques or math. If properly used, the system provides truly unbreakable encryption and it will be impossible for any eavesdropper to decrypt or break one-time pad encrypted message by any type of cryptanalytic attack without the proper key, even with infinite computational power (see section VII.b) However, to ensure the security of the message, it is of paramount importance to carefully read and strictly follow the security rules and advice (see section VII).
    [Show full text]
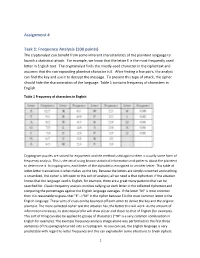
  • Assignment 4 Task 1: Frequency Analysis (100 Points)
    Assignment 4 Task 1: Frequency Analysis (100 points) The cryptanalyst can benefit from some inherent characteristics of the plaintext language to launch a statistical attack. For example, we know that the letter E is the most frequently used letter in English text. The cryptanalyst finds the mostly-used character in the ciphertext and assumes that the corresponding plaintext character is E. After finding a few pairs, the analyst can find the key and use it to decrypt the message. To prevent this type of attack, the cipher should hide the characteristics of the language. Table 1 contains frequency of characters in English. Table 1 Frequency of characters in English Cryptogram puzzles are solved for enjoyment and the method used against them is usually some form of frequency analysis. This is the act of using known statistical information and patterns about the plaintext to determine it. In cryptograms, each letter of the alphabet is encrypted to another letter. This table of letter-letter translations is what makes up the key. Because the letters are simply converted and nothing is scrambled, the cipher is left open to this sort of analysis; all we need is that ciphertext. If the attacker knows that the language used is English, for example, there are a great many patterns that can be searched for. Classic frequency analysis involves tallying up each letter in the collected ciphertext and comparing the percentages against the English language averages. If the letter "M" is most common then it is reasonable to guess that "E"-->"M" in the cipher because E is the most common letter in the English language.
    [Show full text]