Download Download
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Universal Declaration of Human Rights
Hattak Móma Iholisso Ishtaa-aya Ámmo'na Holisso Hattakat yaakni' áyya'shakat mómakat ittíllawwi bíyyi'ka. Naalhpisa'at hattak mómakat immi'. Alhínchikma hattak mómakat ishtayoppa'ni. Hookya nannalhpisa' ihíngbittooka ittimilat taha. Himmaka hattakat aa- áyya'shahookano ilaapo' nanna anokfillikakoot nannikchokmoho anokfillihootokoot yammako yahmichi bannahoot áyya'sha. Nannalhpisa' ihíngbittookookano kaniya'chi ki'yo. Immoot maháa'chi hattakat áyya'sha aalhlhika. Nannalhpisa' ihíngbittooka immoot maháahookya hattakat ikayoppa'chokmat ibaachaffa ikbannokmat ilaapo' nanna aanokfillikakoot yahmichi bannahoot áyya'sha. Hattak mómakat nannaka ittibaachaffa bíyyi'kakma chokma'ni. Hattak yaakni' áyya'shakat nannalhpisa'a naapiisa' alhihaat mómakat ittibaachaffa bíyyi'kakma nanna mómakat alhpi'sa bíyyi'ka'ni. Yaakni' hattak áyya'shakat mómakat nannaka yahmi bannahoot áyya'shakat holisso holissochi: Chihoowaat hattak ikbikat ittiílawwi bíyyi'kaho Chihoowaat naalhpisa' ikbittooka yammako hattakat kanihmihoot áyya'sha bannakat yámmohmihoot áyya'sha'chi. Hattak yaakni' áyya'shakat mómakat yammookano ittibaachaffahookmaka'chi nannakat alhpi'sa bíyyi'ka'chika. Hattak mómakat ithánahookmaka'chi. Himmaka' nittak áyya'shakat General Assemblyat Nanna mómaka nannaka ithánacha ittibaachaffahookmakoot nannaka alhíncha'chikat holisso ikbi. AnompaKanihmo'si1 Himmaka' nittakookano hattak yokasht toksalicha'nikat ki'yo. Hattak mómakat ittíllawwi bíyyi'kacha nanna mómaka ittibaachaffa'hitok. AnompaKanihmo'si2 Hattakat pisa ittimilayyokhacha kaniyaho aamintihookya -
![Hilbert H. Graves S/ ]'Forhert Peace S/ Pressly S](https://docslib.b-cdn.net/cover/9864/hilbert-h-graves-s-forhert-peace-s-pressly-s-99864.webp)
Hilbert H. Graves S/ ]'Forhert Peace S/ Pressly S
Ji REG'UIJ~R MEE'l'II~G Februar}' 2, 1960 TH"B C0!1L"iWN" C01J?'fCIL OF THJ~ CI'l'Y OJ!' B.1.iOON!.lNtxTON, IND.wlJ\Ul, met in the Council Chambers in Cj.ty Hall, on Tuesaa.y, February 2, 1960, at the hour o:r seven-tlurty-o'c!ock {7:30 P.1r. o.s.T.) in reg,111<'.r session with Mayor Thos. L. Lemon presiding. l!Iembers present: Chitwood, Peace, Graves, Stikeleather, Faucett, and Ma,rxson. !,{embers absent: Sili::es. Councilman Gra:ves opened the meeting 1vi th a, prayer. Councilman Graves moved, seconded by Councilman Peace that the minutes of the last regular meeting or January 19, 1960 be approved as submitted to each ind1vidual councilman; motion unuimously carried. Councl.lma,n Graves presented Ordina,nce No.' 4,, 1960 for second' reading an.ct moved., seconded by Councilman Pea,ce that Orctinance No. 4, 196op be reaii by title only." Uponca roll call vote the motion was unanimously ca,rried. After second reacling by t1 tle only, Councilman Graves moved, ~~·"~~.1 seconded by Councilman Ch1twood. that Ordinance No. 4, 1960 be daly adop·tecl. Upon a :roll call vote, Ordin?-nce No. 4, 1960 was unanimously ~'}.'._ adopted. ·~:t' , Council man Graves presented Ordin<u1.:ie No. 5, 1960 for second. reading and moved, seconde;i by Councilinan Pei1ce that Ordinance 7fo. 5, 1960 be gi,ven second i·eading ~yti tle only. Upon a :roll ca.i.l vote the moti on unanimously carried. After second readrng by title only, Councilman Graves moved, seconded by Councilman Peace that Ordinance No. -

Unicode Request for Cyrillic Modifier Letters Superscript Modifiers
Unicode request for Cyrillic modifier letters L2/21-107 Kirk Miller, [email protected] 2021 June 07 This is a request for spacing superscript and subscript Cyrillic characters. It has been favorably reviewed by Sebastian Kempgen (University of Bamberg) and others at the Commission for Computer Supported Processing of Medieval Slavonic Manuscripts and Early Printed Books. Cyrillic-based phonetic transcription uses superscript modifier letters in a manner analogous to the IPA. This convention is widespread, found in both academic publication and standard dictionaries. Transcription of pronunciations into Cyrillic is the norm for monolingual dictionaries, and Cyrillic rather than IPA is often found in linguistic descriptions as well, as seen in the illustrations below for Slavic dialectology, Yugur (Yellow Uyghur) and Evenki. The Great Russian Encyclopedia states that Cyrillic notation is more common in Russian studies than is IPA (‘Transkripcija’, Bol’šaja rossijskaja ènciplopedija, Russian Ministry of Culture, 2005–2019). Unicode currently encodes only three modifier Cyrillic letters: U+A69C ⟨ꚜ⟩ and U+A69D ⟨ꚝ⟩, intended for descriptions of Baltic languages in Latin script but ubiquitous for Slavic languages in Cyrillic script, and U+1D78 ⟨ᵸ⟩, used for nasalized vowels, for example in descriptions of Chechen. The requested spacing modifier letters cannot be substituted by the encoded combining diacritics because (a) some authors contrast them, and (b) they themselves need to be able to take combining diacritics, including diacritics that go under the modifier letter, as in ⟨ᶟ̭̈⟩BA . (See next section and e.g. Figure 18. ) In addition, some linguists make a distinction between spacing superscript letters, used for phonetic detail as in the IPA tradition, and spacing subscript letters, used to denote phonological concepts such as archiphonemes. -

ZONING CERTIFICATE 0006Parcel Depth440
Queen Anne s County 160 Coursevall Drive Centreville MD 21617 Zoning Certificate Z 09 0 7 79 Date 09 14 2009 ZONING CERTIFICATE Location Building 00605 MAIN ST STEVENSVILLE Tax Tax Acct 1804069579 Card 4187 Acreage 76 Subdiv Lot Block Sect Tax Block Zone Map 0056 0006Parcel 0062 VC Frontage 80 Depth440 Owner s Name Home KENT ISLAND STATION LLC Work 410490tl722 10614 BEAVER DAM RD Mailing Address HUNT VALLEY MD 21030 0000 City State Zip Code EXisting Use Proposed Use VACANT UNIT NEW BUSINESS Building Value Application Fee 0 130 00 Type of Sewage Disposal Type of Water Supply PUBLIC SEPTIC Use Permit Critical Area YES I NO I Staked Proposed Work USE PERMIT FOR HOLLAND BROWNLEY ESQUIRE COMMERCIAL OFFICE SUITE 207 250 S F 2 EMPLOYEES 2ND FLR Minimum Yard Requirements Front Rear Side Side ST Heieht Approvals SHA N A DPW fK ELEC I j li Ot RICHARD L CHINA Applicants Name Phone 4104908722 10614 BEAVER DAM RD Address HUNT VALLEY MD 21030 Comments NO NOTES RENOVATION B09 0955 CERTIFICATE OF OCCUPANCY ISSUED 2 22 10 FIRE MARSHAL APPROVAL GJE 2 19 10 This is to certify that this Zoning Certificate is granted this date Administrator Queen Anne s County 160 Coursevall Drive Centreville MD 21617 Zoning Certificate Z09 l780 Date 09 14 2009 ZONING CERTIFICATE Location Building 00605 MAIN ST STEVENSVILLE Tax Acct Tax Card Acreage 1804069579 4187 76 Sect Subdiv Lot Block Tax Block Parcel Zone Frontage Map 0056 0006 0062 VC Owner s Name Home KENT ISLAND STATION LLC Work 4104908722 Mailing Address 10614 BEAVER DAM RD City State Zip Code HUNT VALLEY MD 21030 -

Outboard Motor Safety
02/04/02 16:44:54 31ZW6601_001 The engine exhaust from this product contains chemicals known to the State of California to cause cancer, birth defects, or other reproductive harm. Keep this owner’s manual handy, so you can refer to it at any time. This owner’s manual is considered a permanent part of the outboard motor and should remain with the outboard motor if resold. The information and specifications included in this publication were in effect at the time of approval for printing. Honda Motor Co., Ltd. reserves the right, however, to discontinue or change specifications or design at any time without notice and without incurring any obligation whatever. No part of this publication may be reproduced without written permission. 02/04/02 16:45:01 31ZW6601_002 INTRODUCTION Congratulations on your selection of We suggest you read the warranty a Honda outboard motor. We are policy to fully understand its certain you will be pleased with your coverage and your responsibilities of purchase of one of the finest ownership. The warranty policy is a outboard motors on the market. separate document that should have been given to you by your dealer. We want to help you get the best results from your new outboard When your outboard motor needs motor and to operate it safely. This scheduled maintenance, keep in mind manual contains the information on that your Honda marine dealer is how to do that; please read it specially trained in servicing Honda carefully. outboard motors. Your Honda marine dealer is dedicated to your As you read this manual you will satisfaction and will be pleased to find information preceded by a answer your questions and concerns. -

Whpr19750225-011
Digitized from Box 8 of the White House Press Releases at the Gerald R. Ford Presidential Library FOR IMMEDIATE RELEASE FEBRUARY 25, 1975 OFFICE OF THE 'WHITE HousE PRESSBECRETARY THE WHITE HOUSE," REMARKS OF THE PRESIDENT TO THE \VOMENtS FORUM ON NATIONAL SECURITY WASHINGTON HILTON HOTEL 9: 45 A.M. EDT Mrs. Kubby, la~ies and gentlemen: • ':.."- ,- ,:t 1,;;, It ~s a great pr~v~lege and honop for me,to be here and, to participate in the w6m~n· s' ,r.o~,um on National Security,. and' I thank youvfi,r¥ much for the opportunity. ' , , ~ As I look around the room on thi~ occasion, .-'. -,"- .. ' :.: :.,- .".','. ~t br~ngs back to me, the memor~e~ of pr~v~ous occa$.~ons., So, I know at the' very outset'that; '?e ,sha:rethe ~~~, .' . vision for America, a free rising democracy, and wea:lso share the awareness that only a strong America'can'stay free. 's:'i; I am greatly impressed with the theme of your gathe:ring'-- Peace, a Common Purpose. This· is the link, thaj:brings us together on this occasion and,will be, a link as we move forward to keep America strong and ' prepared to keep the peace. ' Let me expre.ss from the bottom of my heart my than~ for your past efforts to bolster our national. security. As I said earlier, I recall very vividly meeting with your group on previous occasions. You and the two and one-half million women in all of our fifty states, the Philippines, Puerto Rico, Panama-- which all of you represent -- are one of the most potent and effective grass roots lobby we have for a peaceful, , and secure.America, and I congratulate,You for being,here, and for your 'never ending efforts in this yery Jlig;h purpose. -

Language Specific Peculiarities Document for Halh Mongolian As Spoken in MONGOLIA
Language Specific Peculiarities Document for Halh Mongolian as Spoken in MONGOLIA Halh Mongolian, also known as Khalkha (or Xalxa) Mongolian, is a Mongolic language spoken in Mongolia. It has approximately 3 million speakers. 1. Special handling of dialects There are several Mongolic languages or dialects which are mutually intelligible. These include Chakhar and Ordos Mongol, both spoken in the Inner Mongolia region of China. Their status as separate languages is a matter of dispute (Rybatzki 2003). Halh Mongolian is the only Mongolian dialect spoken by the ethnic Mongolian majority in Mongolia. Mongolian speakers from outside Mongolia were not included in this data collection; only Halh Mongolian was collected. 2. Deviation from native-speaker principle No deviation, only native speakers of Halh Mongolian in Mongolia were collected. 3. Special handling of spelling None. 4. Description of character set used for orthographic transcription Mongolian has historically been written in a large variety of scripts. A Latin alphabet was introduced in 1941, but is no longer current (Grenoble, 2003). Today, the classic Mongolian script is still used in Inner Mongolia, but the official standard spelling of Halh Mongolian uses Mongolian Cyrillic. This is also the script used for all educational purposes in Mongolia, and therefore the script which was used for this project. It consists of the standard Cyrillic range (Ux0410-Ux044F, Ux0401, and Ux0451) plus two extra characters, Ux04E8/Ux04E9 and Ux04AE/Ux04AF (see also the table in Section 5.1). 5. Description of Romanization scheme The table in Section 5.1 shows Appen's Mongolian Romanization scheme, which is fully reversible. -

Global Journal of Engineering and Technology Review High
Global Journal of Engineering and Technology Review Journal homepage: www.gjetr.org Global J. Eng. Tec. Review 4 (4) 73 – 81 (2019) High-Throughput of SHA-256 Hash Function with Unfolding Transformation 1* 2 Shamsiah binti Suhaili , Takahiro Watanabe 1 Faculty of Engineering, Universiti Malaysia Sarawak, 94300 Kota Samarahan, Sarawak, Malaysia 2 Graduate School of Information, production and Systems, Waseda University, 2-7 Hibikino, Wakamatsu-ku, Kitakyushu-shi, Fukuoka 808-0135, Japan ABSTRACT Hash Function in cryptography algorithms is used to encrypt the message by giving the appropriate output based on the structure of the hash function itself. This algorithm is important for security application such as Keyed-Hash Message Authentication Code (HMAC), digital signature and others. There are different types of hash function such as MD5, SHA-1, RIPEMD-160, SHA-256, SHA-224, SHA-384, SHA-512 and others. In this paper, the unfolding transformation method was proposed to improve the throughput of the SHA-256 hash function. Three types of SHA-256 hash function were designed namely SHA-256 design, SHA-256 design inner pipelining with unfolding factor 2 and SHA-256 design inner pipelining with unfolding factor 4. The designs were written in Verilog code and the output simulations were verified using ModelSim. The simulation results showed that the proposed SHA-256 inner pipelining unfolding with factor 4 provided the highest throughput which is 4196.30 Mbps, and with factor 2 was superior in terms of maximum frequency and was better than the conventional SHA-256 design. Type of Paper: other. Keywords: Cryptography algorithm; FPGA; SHA-256 Hash Function; Unfolding transformation, Verilog __________________________________________________________________________________ 1. -
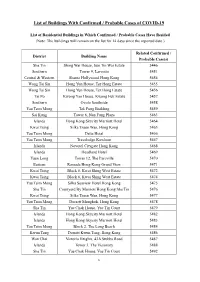
List of Buildings with Confirmed / Probable Cases of COVID-19
List of Buildings With Confirmed / Probable Cases of COVID-19 List of Residential Buildings in Which Confirmed / Probable Cases Have Resided (Note: The buildings will remain on the list for 14 days since the reported date.) Related Confirmed / District Building Name Probable Case(s) Sha Tin Shing Wai House, Sun Tin Wai Estate 5446 Southern Tower 9, Larvotto 5451 Central & Western Shama Hollywood Hong Kong 5454 Wong Tai Sin Hong Yun House, Tsz Hong Estate 5455 Wong Tai Sin Hong Yun House, Tsz Hong Estate 5456 Tai Po Kwong Yan House, Kwong Fuk Estate 5457 Southern Ovolo Southside 5458 Yau Tsim Mong Tak Fung Building 5459 Sai Kung Tower 6, Nan Fung Plaza 5463 Islands Hong Kong Skycity Marriott Hotel 5464 Kwai Tsing Silka Tsuen Wan, Hong Kong 5465 Yau Tsim Mong Delta Hotel 5466 Yau Tsim Mong Travelodge Kowloon 5467 Islands Novotel Citygate Hong Kong 5468 Islands Headland Hotel 5469 Yuen Long Tower 12, The Parcville 5470 Eastern Ramada Hong Kong Grand View 5471 Kwai Tsing Block 6, Kwai Shing West Estate 5472 Kwai Tsing Block 6, Kwai Shing West Estate 5474 Yau Tsim Mong Silka Seaview Hotel Hong Kong 5475 Sha Tin Courtyard By Marriott Hong Kong Sha Tin 5476 Kwai Tsing Silka Tsuen Wan, Hong Kong 5477 Yau Tsim Mong Dorsett Mongkok, Hong Kong 5478 Sha Tin Yue Chak House, Yue Tin Court 5479 Islands Hong Kong Skycity Marriott Hotel 5482 Islands Hong Kong Skycity Marriott Hotel 5483 Yau Tsim Mong Block 2, The Long Beach 5484 Kwun Tong Dorsett Kwun Tong, Hong Kong 5486 Wan Chai Victoria Heights, 43A Stubbs Road 5487 Islands Tower 3, The Visionary 5488 -

Piecing Together Sha Po: Archaeological Investigations and Landscape Reconstruction
BOOK REVIEWS 321 and abstract ideas. As such, Pristine Affluence HORKY,PHILLIP S. provides a lesson to us all, not in how to escape 2009 Persian cosmos and Greek philosophy: Plato’s associates and the Zoroastrian society, but in how we might work to magoi. Oxford Studies in Ancient strengthen the community of academe. Philosophy 37:47–103. LEE,RICHARD B., AND IRVEN DEVORE REFERENCES CITED 1968 Man the Hunter. New York: Transaction Publishers. ASHMAN ATHARINE AND HANE RONIN C ,K V. , S J. C SAHLINS,MARSHALL 2008 Welcoming a monster to the world: 1972 Stone Age Economics. London: Tavi- Myths, oral tradition, and modern stock. societal response to volcanic disasters. Journal of Volcanology and Geothermal SCHNAPP,ALAIN Research 176(3):407–418. 1996 The Discovery of the Past. London: British Museum Press. ELTSOV,PIOTR A. 2016 The ghost of the state in deep antiquity: SCOTT,JAMES C. A closer look at the Harappan Civiliza- 2017 Against the Grain: A Deep History of tion from the viewpoint of Sanskrit the Earliest States. New Haven: Yale literature, in Connections and Complex- University Press. ity: New Approaches to the Archaeology of – VERELLEN,FRANCISCUS, ED. South Asia: 299 314, ed. S. A. 1998 Culte des sites et culte des saints en Abraham, P. Gullapalli, T. P. Raczek, Chine [Worship sites and cults of saints and U. Z. Rizvi. Walnut Creek, CA: in China]. Cahiers d’Extrême-Asie, Left Coast Press. special issue 10(1). Piecing Together Sha Po: Archaeological Investigations and Landscape Reconstruction. Mick Atha and Kennis Yip. Hong Kong: Hong Kong University Press, 2016. -

1 Phün Tsok Ge Lek Che Wai Trün Pey Ku Thar
SONGS OF SPIRITUAL EXPERIENCE - Condensed Points of the Stages of the Path - lam rim nyams mgur - by Je Tsongkapa 1 PHÜN TSOK GE LEK CHE WAI TRÜN PEY KU THAR YE DRO WAI RE WA KONG WEY SUNG MA LÜ SHE JA JI ZHIN ZIK PEY THUK SHA KYEY TSO WO DE LA GO CHAK TSEL Your body is created from a billion perfect factors of goodness; Your speech satisfies the yearnings of countless sentient beings; Your mind perceives all objects of knowledge exactly as they are – I bow my head to you O chief of the Shakya clan. 2 DA ME TÖN PA DE YI SE KYI CHOK GYAL WAI DZE PA KÜN GYI KUR NAM NE DRANG ME ZHING DU TRÜL WAI NAM RÖL PA MI PAM JAM PAI YANG LA CHAK TSEL LO You’re the most excellent sons of such peerless teacher; You carry the burden of the enlightened activities of all conquerors, And in countless realms you engage in ecstatic display of emanations – I pay homage to you O Maitreya and Manjushri. 3 SHIN TU PAK PAR KAR WA GYAL WAI YUM JI ZHIN GONG PA DREL DZE DZAM LING GYEN LU DRUB THOK ME CHE NI SA SUM NA YONG SU TRAK PEY ZHAB LA DAG CHAK TSEL So difficult to fathom is the mother of all conquerors, You who unravel its contents as it is are the jewels of the world; You’re hailed with great fame in all three spheres of the world – I pay homage to you O Nagarjuna and Asanga. -

Oregon Oddities
IRER (1) 4- OREGON ODDITIES and ITEMS OF INTEREST For us by teachers, students, libraries,and. publications Please iv credit to th inforxiatioi rvice of The Fedra1 Writrs' and HistoricalRecords Survey Projects of the 1QV5PROGRESS ADirISTRATION OF CRE&3N 4OElks Euildin Portland, Oregon The itens in this bulletin, selected from the matorial compiled by the Feera1 Writers' Projectaid the t Ristorical Records Survey of the Works ProgressAdministration, t are representative of the àignificant pollections being made by these rationwide progreins. The Historical Records Survey isinventorying all sources of earlr Oregon history, including county andstate record, church archives, historic cemeteries, old manuscripts and imprints, - old printingrezses, monuments and relics, private diaries,letter, s and memoirs, historic buildings, and Indianrecords and lore. T-he chief undertaking of the FederalWriters' Project has been theerican Guide Series of books.In Oregon as in all other states the work includes the state Guide,designed to ac- 2 quaintnericans Withnerica and to present. to the visitor the history, indistry,ecreati onal advantages- and scenic attractions of the state. A- The Oregon Guide,now in thefinal stages of editing LC will soon be added to the list of thosealready published which et includes Idaho:A Guide in Word and Picture; Maine:A Guide "Down East"; Massachusetts:A Guide to its Places and People; New Hamp- DIE shire:A Guide to the Graite State; Washington:City and Capital; PC Philadelphia:A Guide to the Birthplace ofa Nation. tI A HI SIQFI C Vr0NUMENT S While livir-g at Salemhe hauled " don't know anything about toib- helped to trans- 3tones.We deal in monuments," declared freight to Portland, and .H.