DOCSLIB.ORG

P2.2. Music Temperaments Evaluation Based on Triads

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
P2.2. Music Temperaments Evaluation Based on Triads Music Temperaments Evaluation Based on Triads Tong Meihui Tojo Satoshi JAIST JAIST [email protected] [email protected] ABSTRACT Ogata [4] has proposed the idea of consonance value among chords, calculating the consonance value of each two tones It is impossible for one temperament to achieve optimally in the triads and adding them up, and then drew a 3D dis- both of consonance and modulation. The dissonance level sonance curve of the chords. Also, Cook [5] showed the has been calculated by the ratio of two pitch frequencies, acoustical properties of triads, claiming the perception of however in the current homophonic music, the level should harmony is not simply a sum of inner consonance. In this be measured by chords, especially by triads. In this re- research, we revise the Ogata’s calculation and formalize search, we propose to quantify them as Dissonance Index the dissonance level in a more rigorous way. of Triads (DIT). We select eight well-known temperaments This paper is organized as follows. In the following sec- and calculate seven diatonic chords in 12 keys and compare tion, we show preliminaries including the introduction of the weighted average and standard deviation to quantify various temperaments. Thereafter, we propose our formal- the consonance, and then we visualize our experimental re- ization and show its visualization. Then, we analyze the sults in a two-dimensional chart to compare the trade-offs results, and finally conclude. between consonance and modulation. 2. PRELIMINARIES 1. INTRODUCTION 2.1 Scale and Temperaments Nowadays, 12-tone equal temperament is prevalent and other temperaments has fallen to only historical and math- A set of notes employed in a music piece is, when arranged ematical interests. However, even now in the actual perfor- in a pitch order in an octave, is called a scale. The ratio of mance, string and wind instruments are played in an ad hoc frequency of two pitches is fixed by natural science disci- adjustment of pitches unless accompanied by keyboard in- plines such as physical science, acoustics, and psychology, struments. In this age, those electronic instruments ease among which mathematics plays the most important role, us in using any scale more freely. Then, our motivation in and one fixed series of ratios in a scale gives the notion of this paper is to give quantitative understanding to the dis- temperament. sonance level in various temperament in terms of triads. Pythagoras in ancient Greece discovered that the perfect The difference of temperaments has been often mentioned fifth interval with the frequency ratio of 3:2 as the most by the ratio of two pitch frequencies and such web site as consonant, next to the octave of 2:1, around 550 BC [6]. Pianoteq 1 provides us a very convincing interface to ex- The Sanfen Sunyi-fa by Jing Fang in China (BC77–BC37) perience the difference of temperaments; however, there is considered to have invented the same temperament with were no mathematical formulation to evaluate the conso- Pythagorean tuning [7]. nance and modulation 2 of a chord. Since then, musicologists have been constantly exploring Consonance and dissonance are ambiguous psychologi- how to solve the problem of Pythagorean comma, that is cal notions. The purpose of this research is to explore the the error which slightly exceeds the octave when the 12th mathematical model of Dissonance Index of Triads (DIT). tone is introduced by multiples of 3/2. If we perempto- In 1863, Helmholtz [1] proposed the mathematical model rily regard the 12th locates at the octave, the interval be- of consonance and dissonance in tones in terms of beats tween the 11th and the 12th becomes narrower than the and roughness. In 1965, Plomp and Levelt [2] defined the other fifths. In later years, Pythagoras pitch was amended dissonance curve between two pure tones. Later, the math- to place the narrow fifth, so called the wolf fifth 3 , between ematical formula of the curve has been improved, and Vas- G] and D] where the fifth is rarely used. silakis [3] claimed that the formula he proposed had been The ultimate temperament for consonance is the just in- believed to be most reliable; and thus, we employ it also in tonation, introducing the multiple by 5 in addition to 3/2, this paper, though adding the effect of overtones. where the ratio between the intervals can be expressed all by small integers [8]. However, in contrast, the just intona- 1 https://www.pianoteq.com/ 2 In this paper, the modulation means a key transposition. tion is very clumsy in modulation. The scale evolved into the mean-tone systems [9, 10], well-temperaments by An- dreas Werckmeister (1645–1706) [11] or by Johann Philipp Copyright: c 2019 Tong Meihui et al. This is an open-access article distributed Kirnberger (1721–1783) [12], and since then there exist under the terms of the Creative Commons Attribution 3.0 Unported License, which hundreds or even thousands of music temperaments. permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. 3 It is named after the unpleasant sound like the roaring of wolves. C bDD bEEF #FG bAA bBB 37 9 39 81 311 729 3 212 27 215 243 Sanfen Sunyi-fa 1 211 8 214 64 217 512 2 38 16 310 128 256 9 32 81 4 729 3 128 27 16 243 Pythagorean Tuning 1 243 8 27 64 3 512 2 81 16 9 128 16 9 6 5 4 45 3 8 5 16 15 Just Intonation 1 15 8 5 4 3 32 2 5 3 9 8 1 6 3 5 3 2 2 4 1 4 2 4 2 5 2 5 2 5 4 8 5 2 5 Quarter-Comma Meantone 1 5 2 3 4 1 23 5 5 2 1 22 5 4 5 4 5 4 5 2 7 1 6 3 5 4 2 2 4 1 2 4 2 4 5 5 2 5 2 5 4 5 5 2 5 Conventional QC Meantone 1 24 2 3 4 1 23 5 24 2 1 22 5 4 5 4 5 2 p p p p p 28 64 2 32 213 4 2 4 210 8 4 8 128 210 4 2 16 128 4 2 Werckmeister 1 35 81 27 38 3 36 9 81 36 9 81 p 135 9 32 5 4 45 3 128 3 5 16 15 Kirnberger 1 128 8 27 4 3 32 2 81 4 9 8 1 2 3 4 5 6 7 8 9 10 11 Equal Temperament 1 2 12 2 12 2 12 2 12 2 12 2 12 2 12 2 12 2 12 2 12 2 12 Table 1: Ratios of Temperaments in Fractions The equal temperament has been the product of compro- mise, which systematically compensated the Pythagorean comma, defining each half tone to be the 12th root of 2. Then, the temperament perfectly eased the modulation, that is, to enable us to change from one key to another freely, and was applied to the tuning of most modern musical in- struments around the world. But we can never say that the equal temperament is satisfactory because it rejects the original intention of the temperament, viz., the consonance between intervals. Table1 lists the frequency ratios of some typical music temperaments introduced above. 2.2 Helmholtz’s Theory of Beats In physics, the superposition of two simple sinusoidal waves with similar but slightly different frequency will cause pe- Figure 1: Dissonance Curve From a Fixed Tone to Another riodic fluctuation in strength through time. This phenomenon Tone [2] is known to piano tuners as beats. Hermann Helmholtz [1] concluded that dissonance is produced by the beats be- tween two pure tones (without overtones) or between a pair of dissonance, and the interval is from 0 to 1 from top to of partials of two complex sounds. bottom. The lower the vertical value is in this figure, the When the difference in frequency is small, the beats can more dissonant. The horizontal axis is the frequency dif- be easily heard. As the difference is increased to 20-30 ference between higher tone and the base tone, divided by Hz, the beats will create the impression like ‘jarring and the value of the critical bandwidth. As the frequency dif- rough’ described by Helmholtz. Beyond this approximate ference gradually becomes larger, we can observe the re- point, the beats gradually become too rapid to be identified sult of the dissonance value d between the two pure tones and the sensation of roughness disappears. varying. The most dissonant position (d = 1) is said to be about a quarter of the critical band. When the frequency of the tone is too high or too low 2.3 Dissonance Curve to be heard by human ears, the identification of the tones In 1965, Plomp and Levelt confirmed Helmholtz’s hypoth- becomes not that easy. When the horizontal axis of the dis- esis by several experiments [2]. They plotted the disso- sonance curve only takes the frequency difference (without nance curve and proposed the concept of critical band- divided by critical bandwidth), we need to draw many dif- width. Note that though the sound produced by the mu- ferent graphs according to the difference of base tones. sical instruments has a complex timbre this psychologi- cal experiment employed only pure tones with the simplest 2.4 Numerical Calculation of Dissonance in Two spectrum. The combined experimental results is shown in Tones Figure1, and nowadays this result is widely accepted.
Load more

Recommended publications
  • John Corigliano's Fantasia on an Ostinato, Miguel Del Aguila's Conga for Piano, and William Bolcom's Nine New Bagatelles
    Graduate Theses, Dissertations, and Problem Reports 2016 Pedagogical and Performance Aspects of Three American Compositions for Solo Piano: John Corigliano's Fantasia on an Ostinato, Miguel del Aguila's Conga for Piano, and William Bolcom's Nine New Bagatelles Tse Wei Chai Follow this and additional works at: https://researchrepository.wvu.edu/etd Recommended Citation Chai, Tse Wei, "Pedagogical and Performance Aspects of Three American Compositions for Solo Piano: John Corigliano's Fantasia on an Ostinato, Miguel del Aguila's Conga for Piano, and William Bolcom's Nine New Bagatelles" (2016). Graduate Theses, Dissertations, and Problem Reports. 5331. https://researchrepository.wvu.edu/etd/5331 This Dissertation is protected by copyright and/or related rights. It has been brought to you by the The Research Repository @ WVU with permission from the rights-holder(s). You are free to use this Dissertation in any way that is permitted by the copyright and related rights legislation that applies to your use. For other uses you must obtain permission from the rights-holder(s) directly, unless additional rights are indicated by a Creative Commons license in the record and/ or on the work itself. This Dissertation has been accepted for inclusion in WVU Graduate Theses, Dissertations, and Problem Reports collection by an authorized administrator of The Research Repository @ WVU. For more information, please contact [email protected]. Pedagogical and Performance Aspects of Three American Compositions for Solo Piano: John Corigliano’s Fantasia on an Ostinato, Miguel del Aguila’s Conga for Piano, and William Bolcom’s Nine New Bagatelles Tse Wei Chai A Doctoral Research Project submitted to The College of Creative Arts at West Virginia University in partial fulfillment of the requirements for the degree of Doctor of Musical Arts in Piano Performance James Miltenberger, D.M.A., Committee Chair & Research Advisor Peter Amstutz, D.M.A.
    [Show full text]
  • Computational Methods for Tonality-Based Style Analysis of Classical Music Audio Recordings
    Fakult¨at fur¨ Elektrotechnik und Informationstechnik Computational Methods for Tonality-Based Style Analysis of Classical Music Audio Recordings Christof Weiß geboren am 16.07.1986 in Regensburg Dissertation zur Erlangung des akademischen Grades Doktoringenieur (Dr.-Ing.) Angefertigt im: Fachgebiet Elektronische Medientechnik Institut fur¨ Medientechnik Fakult¨at fur¨ Elektrotechnik und Informationstechnik Gutachter: Prof. Dr.-Ing. Dr. rer. nat. h. c. mult. Karlheinz Brandenburg Prof. Dr. rer. nat. Meinard Muller¨ Prof. Dr. phil. Wolfgang Auhagen Tag der Einreichung: 25.11.2016 Tag der wissenschaftlichen Aussprache: 03.04.2017 urn:nbn:de:gbv:ilm1-2017000293 iii Acknowledgements This thesis could not exist without the help of many people. I am very grateful to everybody who supported me during the work on my PhD. First of all, I want to thank Prof. Karlheinz Brandenburg for supervising my thesis but also, for the opportunity to work within a great team and a nice working enviroment at Fraunhofer IDMT in Ilmenau. I also want to mention my colleagues of the Metadata department for having such a friendly atmosphere including motivating scientific discussions, musical activity, and more. In particular, I want to thank all members of the Semantic Music Technologies group for the nice group climate and for helping with many things in research and beyond. Especially|thank you Alex, Ronny, Christian, Uwe, Estefan´ıa, Patrick, Daniel, Ania, Christian, Anna, Sascha, and Jakob for not only having a prolific working time in Ilmenau but also making friends there. Furthermore, I want to thank several students at TU Ilmenau who worked with me on my topic. Special thanks go to Prof.
    [Show full text]
  • Music Theory Syllabus (With Introduction to Music) Frenship
    Music Theory Syllabus (with Introduction to Music) 1306.030 Frenship High School Blue Days 12:54-2:24pm 2020-2021 Instructor: Angela Bradford Office: Room 1316 Phone: 806-866-4440, ext. 1028 Email: [email protected] Remind: Text to 81010 and message @329a99b Conference Times: 2:30-4:00pm, Blue and Gold days Course Text: Tonal Harmony by Stefan Kostka, Dorothy Payne and Byron Almen, 7th Edition. (Provided) Supplemental Material: Barron’s AP Music Theory by Nancy Scoggin (Optional) Course Purpose: The purpose of this Dual Credit course is to teach the language of Music Theory to students and help them develop the skills and knowledge to build students music literacy (reading, writing, hearing intelligently, and respond or performing) through analysis and composition. Course Overview: A) Oral Quizzes B) Score analysis C) Error Detection D) Aural association E) Association with familiar music Grading: 50% Written theory and composition- Daily Work (Fundamentals and Analysis) and Assessment Grades – 25% Composition 1 – 5%, Composition 2 – 5%, Composition 3 - 15% 30% Ear training – Intervals, Inversions, Chords, Scales on Assessment and quiz grades 20% Oral training (Sight-Reading), music literature and history (composers and music periods), and piano fundamentals in practice (chords, scales in major and minor, intervals) Course Outline: 1st Six Weeks Week 1 (2-3 class meetings - 1hr. 30 minutes class) Chap. 1 Elements of Pitch and Chap. 2 Elements of Rhythm 1 Notation a) The aspects of sound: pitch, amplitude, timbre, envelope (articulation) and duration. b) After a brief explanation of each, discuss aspects of notation as they relate to aspects of sound.
    [Show full text]
  • Tonality and Modulation
    Theory Dr. Crist Tonality and Modulation Tonality - The hierarchical relationship of tones to a pitch center or "tonic." Tonal music involves the use of twelve major and twelve minor keys, the scales that comprise these keys, and the tertian harmonies generated from the notes of these scales. A harmony may be constructed on each of the seven diatonic scale degrees resulting in seven different harmonic functions. The seven different functions exhibit varying levels of strength but all serve to support the tonic which is embodied in the tonic triad. Tonality is achieved through a variety of means. The strongest tonality would involve: (1) Only diatonic pitches. (2) A pitch center (tonic) which exhibits a sense of stability and to which all tonal movement flows. (3) Strong cadences. Perfect authentic cadences (PAC) especially. (4) Begin and end with the tonic key. (5) Pedal points and ostinatos which involve reiteration of the tonic scale degree. (6) Strong harmonic progressions. In particular, dominant to tonic progressions which involve the leading-tone resolution to tonic. (7) Doubling of the tonic pitch. The tonic is given long rhythmic durations. The tonic appears in the outer voices. The tonic is framed by neighboring tones. The following progression employs many of the above mentioned techniques creating a strong sense of C major. PAC I IVP I V7 I I6 IV V7 I Modulation - The process of moving from one key to another. There must be a distinct aural shift from the original key to some other key center. A modulation consists of three parts: (1) a tonality is confirmed, (2) the tonal center changes, (3) a new tonality is confirmed by a cadence in that tonality.
    [Show full text]
  • Parallel Keys and Remote Modulation in Selected String
    1 MacKay, James. “Another Look at Chromatic Third-Related Key Relationships in Late Haydn: Parallel Keys and Remote Modulation in Selected String Quartet Minuets.”.” HAYDN: Online Journal of the Haydn Society of North America 8.2 (Fall 2018), http://haydnjournal.org. © RIT Press and Haydn Society of North America, 2018. Duplication without the express permission of the author, RIT Press, and/or the Haydn Society of North America is prohibited. Another Look at Chromatic Third-Related Key Relationships in Late Haydn: Parallel Keys and Remote Modulation in Selected String Quartet Minuets by James MacKay Loyola University Abstract As asserted by Ethan Haimo in a 1990 article, Joseph Haydn’s Piano Trio in A-flat major, Hob. XV: 14 (1789-90), comprises his first use of a chromatic third relationship between movements of an instrumental work, with a I—flat VI—I tonal plan. This harmonic strategy, immediately taken up by Beethoven in his Piano Trio in G major, Op. 1 no. 2 (slow movement in E, VI) and his Piano Sonata in C major, Op. 2 no. 3 (slow movement in E, III), quickly became a conventional feature of early 19th-century tonality. Such third-related shifts in Haydn’s instrumental music occur earlier than 1790, especially in his string quartet Minuet-Trio movements, often built around a parallel major-parallel minor pairing of keys and their relatives. For instance, in Haydn’s String Quartet in F major, Op. 50 no. 5 (Der Traum), third movement, Haydn effects a chromatic third modulation in two stages: touching briefly upon the parallel key (f minor) in the trio, then moving immediately to its relative major, A-flat (i.e.
    [Show full text]
  • Enharmonic Paradoxes in Classical, Neoclassical, and Popular Music By
    Enharmonic Paradoxes in Classical, Neoclassical, and Popular Music by Haley Britt Beverburg Reale A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy (Music: Theory) in The University of Michigan 2011 Doctoral Committee: Associate Professor Ramon Satyendra, Chair Professor Walter T. Everett Professor Kevin E. Korsyn Professor Herbert Graves Winful Associate Professor Wayne C. Petty © Haley Britt Beverburg Reale 2011 Dedication36B To my husband ii Acknowledgements37B I could not have completed this dissertation without the support of numerous people. I would especially like to thank my adviser, Ramon Satyendra, for his encouragement and boundless optimism through the whole process. He never failed to receive my ideas with enthusiasm and give me the confidence to pursue them, and his wide-ranging knowledge and helpful suggestions sparked many bursts of creativity over the past several years. I would also like to thank the other members of my dissertation committee— Kevin Korsyn, Wayne Petty, Walter Everett, and Herbert Winful—for their advice and support. Their expertise in diverse subjects was invaluable to me, and they were always willing and able to answer my many questions. I also had the privilege of working with and being inspired by many other faculty members at the University of Michigan. Special thanks to Karen Fournier for being a sounding board for many of my research ideas and for being a great listener. Additionally, I would like to acknowledge the Rackham School of Graduate Studies, especially Dean Steven M. Whiting, for financial support throughout my time at the University of Michigan. The teaching assistantships, fellowships, and travel grants for presenting at conferences gave me the means to pursue my research.
    [Show full text]
  • 131 with G in the Bass, Shown Below in Example 4.9. As with the G Minor
    with G in the bass, shown below in Example 4.9. As with the G minor that never arrived, C minor would have been closely related to the home key. This time, however, it would have been as its submediant instead of its mediant. Finally, landing on C minor instead of C major would have avoided the enharmonic paradox on pitch-class 4. Beginning of B section mm. 32 – 33 c: VI V11 I C minor anticipated C major arrives (A¼ and E¼) Example 4.9 Poulenc, Piano Concerto, second movement, first part of B section, mm. 32–33, anticipation of the minor mode and unexpected arrival of C major The primary key areas of this first part of the B section, C major, E major, and A¼ major, are summarized in Example 4.10. The keys tonicized for a shorter duration, shown as quarter notes, are included to show relationships with the main keys. Justification for relating C major back to G major, instead of giving it its own major- minor complex, will be given below. 131 B section (part 1): Mm. 33 35 37 40 45 46 transition first theme 1 2 E¼/e¼: (key of IV or iv……………..........) G/g: IV A¼/a¼: ii i VI i I Example 4.10 Poulenc, Piano Concerto, second movement, key relations in the first part of the B section Parallel modes and the chromatic mediants they support thwart expectations and emerge as the main point of tension for the entire movement. The second half of the B section has the loudest dynamics in the movement thus far, with fortissimo and fortississimo entrances of the theme, double-dotted rhythms, flights into the high registers in the solo part, and frequent harmonic moves to remote keys.
    [Show full text]
  • Neoclassicism 8 Copy
    THREE NEOCLASSICAL COMPOSITIONS FOR VIOLIN AND PIANO: STRAVINSKY’S DUO CONCERTANTE, PROKOFIEV’S VIOLIN SONATA NO. 2 IN D MAJOR, AND POULENC’S VIOLIN SONATA OP. 119 by JONG AH MOON (Under the Direction of Levon Ambartsumian) ABSTRACT In the early part of the twentieth century, the Neoclassical style was a strong influence on violin works by composers such as Igor Stravinsky, Francis Poulenc, and Sergei Prokofiev. Through a recording project and an accompanying document, I will introduce distinctive styles of Neoclassical violin music within three works: Stravinsky’s Duo concertante (1932), Prokofiev’s Violin Sonata No. 2 in D Major, Op. 94 bis (1943), and Poulenc’s Violin Sonata, Op. 119 (1942-1943). Through the performance and discussion, I explore ways to interpret these works in light of their Neoclassical elements. INDECX WORDS: Neoclassicism, Neoclassical violin music, Igor Stravinsky, Sergei Prokofiev, Francis Poulenc, Duo concertante, Violin Sonata No. 2, Violin Sonata Op. 119. THREE NEOCLASSICAL COMPOSITIONS FOR VIOLIN AND PIANO: STRAVINSKY’S DUO CONCERTANTE, PROKOFIEV’S VIOLIN SONATA NO. 2 IN D MAJOR, AND POULENC’S VIOLIN SONATA OP. 119 by JONG AH MOON B. Mus., Ewha Womans University, South Korea, 2006 M.M., New England Conservatory, 2008 A Document Submitted to the Graduate Faculty of The University of Georgia in Partial Fulfillment of the Requirements for the Degree DOCTOR OF MUSICAL ARTS ATHENS, GEORGIA 2013 © 2013 Jong Ah Moon All Rights Reserved THREE NEOCLASSICAL COMPOSITIONS FOR VIOLIN AND PIANO: STRAVINSKY’S DUO CONCERTANTE, PROKOFIEV’S VIOLIN SONATA NO. 2 IN D MAJOR, AND POULENC’S VIOLIN SONATA OP.
    [Show full text]
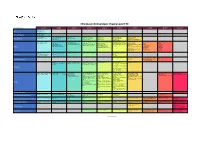
  • Elite Music Online Music Theory Level 1-10
    Elite Music Online Music Theory Level 1-10 Last published: July 2020 Level 1 Level 2 Level 3 Level 4 Level 5 Level 6 Level 7 Level 8 Level 9 Level 10 • Note Values and Rhythm • Note Names Notes • The Grand Staff • Accidentals • 5-Finger Patterns 5-Finger Patterns • 5-Finger Triads • Key Signatures • Order of Sharps and Flats • Major Keys: B, E♭ • Parallel Key Signatures • Enharmonics • Double Accidentals • The Circle of Fifths • Major Keys: C, G, D, F • Major Keys: A, E, B♭ • Minor Keys: E, D • Major Keys: F♯, A♭, D♭, G♭ • Major Keys: C♯, C♭ • Basics of Modulation • All Major Keys Key Signatures • Minor Keys: A • Minor Keys: B, G, C • Minor Keys: F • All Major Keys • Minor Keys: C♯, D♯, E♭, G♯, A♭, • Minor Keys: F♯, B♭ A♯ • Basics of Major Scales • Basics of Natural and Harmonic • Major Scales: B, E♭ • Scale Degrees • Basics of Melodic Minor Scales • Natural Minor Scales: F♯, B♭ • Whole-tone Scales • Modal Scales: • Modal Scales: • Major Scales: C, G, D, F Minor Scales • Natural Minor Scales: E, D • Major Scales: F♯, A♭, D♭, G♭ • Chromatic Scales • Harmonic Minor Scales: F♯, B♭ • Basics of Modes G Ionian F Ionian • Major Scales: A, E, B♭ • Harmonic Minor Scales: E, D • Natural Minor Scales: B, G, C • Major Scales: C♯, C♭ • Melodic Minor Scales: B, E, D, • Natural Minor Scales: C♯, D♯, E♭, A Dorian G Dorian E and B Phrygian A Phrygian • Natural Minor Scales: A • Harmonic Minor Scales: B, G, C • Natural Minor Scales: F G, F♯, B♭ G♯, A♭, A♯ • Harmonic Minor Scales: A • Harmonic Minor Scales: F • Harmonic Minor Scales: C♯, D♯, C and F Lydian
    [Show full text]
  • High School Music Theory Curriculum BOE Adopted
    Content Area Course: Music Theory Grade Level: 9-12 Music Theory R14 The Seven Cs of Learning Collaboration Character Communication Critical Citizenship Thinking Creativity Curiosity Unit Titles Length of Unit • The Basics of Music Theory • 2-3 Weeks • Rhythm & Meter • 2-3 Weeks • Scales & Key Signatures • 3-4 Weeks • Intervals • 3- 4 Weeks • Chords • 3-4 Weeks 1 Region 14 Curriculum: High School Music Theory Curriculum BOE Adopted Strands Course Level Expectations Create • The understanding that creative ideas, concepts, and feelings that influence musicians’ work emerge from a variety of sources. • Musicians’ creative choices are influenced by their expertise, context, and expressive intent. • Musicians evaluate, and refine their work through openness to new ideas, persistence, and the application of appropriate criteria. • Musicians’ presentation of creative work is the culmination of a process of creation and communication. Perform • Performers’ interest in and knowledge of musical works, understanding of their own technical skill, and the context for a performance influence the selection of repertoire. • Analyzing creators’ context and how they manipulate elements of music provides insight into their intent and informs performance. • Performers make interpretive decisions based on their understanding of context and expressive intent. • To express their musical ideas, musicians analyze, evaluate, and refine their performance over time through openness to new ideas, persistence, and the application of appropriate criteria. • Musicians judge performance based on criteria that vary across time, place, and cultures. Respond • Individuals' selection of musical works is influenced by their interests, experiences, understandings, and purposes. • Can respond to music that is informed by analyzing context (social, cultural, and historical) and how creators and performers manipulate the elements of music.
    [Show full text]
  • Formal Mixture in the Sonata-Form Movements of Middle- and Late-Period Beethoven James S
    Document generated on 09/27/2021 3:30 a.m. Intersections Canadian Journal of Music Revue canadienne de musique Formal Mixture in the Sonata-Form Movements of Middle- and Late-Period Beethoven James S. MacKay Contemplating Caplin Article abstract Volume 31, Number 1, 2010 Modal mixture is defined as a local colouration of a diatonic progression by borrowing tones or chords from the parallel major or minor tonality. In his URI: https://id.erudit.org/iderudit/1009287ar efforts to expand tonal resources, Beethoven took this technique further: he DOI: https://doi.org/10.7202/1009287ar borrowed large-scale tonal processes from a composition’s parallel tonality, a technique that I term formal mixture. After tracing its origin to certain works See table of contents by J. S. Bach, C. P. E Bach, Domenico Scarlatti, and Joseph Haydn, I demonstrate how Beethoven built upon his predecessors’ use of the technique throughout his career, thereby expanding and diversifying the tonal resources of late classical era sonata forms. Publisher(s) Canadian University Music Society / Société de musique des universités canadiennes ISSN 1911-0146 (print) 1918-512X (digital) Explore this journal Cite this article MacKay, J. S. (2010). Formal Mixture in the Sonata-Form Movements of Middle- and Late-Period Beethoven. Intersections, 31(1), 77–99. https://doi.org/10.7202/1009287ar All Rights Reserved © Canadian University Music Society / Société de musique This document is protected by copyright law. Use of the services of Érudit des universités canadiennes, 2012 (including reproduction) is subject to its terms and conditions, which can be viewed online. https://apropos.erudit.org/en/users/policy-on-use/ This article is disseminated and preserved by Érudit.
    [Show full text]
  • White Paper Feather Keys
    White Paper Feather Keys: The forgotten and ignored drive component Copyright 2009 by Rino Mechanical See us at www.rinomechanical.com Mechanical Components Inc. 216 North Main Street, Freeport, NY 11520 Phone: (516) 867-5665 Fax: (516) 867-5656 Feather Keys: The Forgotten and Ignored Drive Component With all of the unique components and unique materials coming at engineers these days, some of the simple but very effective ways of the past have been pushed aside. Some of these approaches, such as the Feather Key, must be re-examined to show why they should be considered again. Shaft Keys, sometimes called Sunk Keys are used in power transmission to trans- mit torque between a shaft and a shaft mounted component such as a gear or pulley. Both the shaft and the component must be machined with a keyway of the appropriate size and style for the key to be used. Shaft keys are available in a variety of types and include Parallel Keys, Square Keys, Flat Keys, Rectangular Keys, Woodruff Keys, Plain Taper Keys, Gib-Head Taper Keys, Perpendicular Pins and the Feather Key. Parallel Keys Parallel Keys are sometimes called Straight Keys. These include Square Keys, Rect- angular Keys. They are the most common keys used in industry. When Parallel keys are used the shaft is usually key slotted for the full length of the shaft or slot- ted from the end of the shaft and along the length of the shaft for a distance greater than the length of the key to be used. Parallel keys can be installed by lining up the keyslots in the shaft and the component and then pressing the parallel key between the slots.
    [Show full text]