DOCSLIB.ORG

A Solution and Solid State Study of Niobium Complexes University Of

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Solution and Solid State Study of Niobium Complexes University Of A solution and solid state study of niobium complexes by Leandra Herbst A dissertation submitted to meet the requirements for the degree of Magister Scientiae in the Department of Chemistry Faculty of Natural- and Agricultural Sciences at the University of the Free State Supervisor: Prof. Andreas Roodt Co-Supervisor: Prof. Hendrik G. Visser January 2012 Acknowledgements First and foremost, I thank God Almighty for the countless blessings he has given me. Thank you to Prof. Roodt for all the opportunities, patience and endless enthusiasm for chemistry, inspiring me to learn as much as I can. It is truly an honour to be known as one of your students. To Prof. Deon Visser, thank you for all your guidance and encouragement. Your neverending patience and willingness to give advice is what kept me motivated throughout my studies. To Dr. Linette Bennie, thank you for your guidance with the niobium NMR throughout this project. Thank you to all my colleagues in the Inorganic group for all the laughter and jokes. Thank you for sharing your knowledge and for your patience when having to explain something several times. Every one of you contributed to this study in some way and for that I thank you. To my father, Lucas Herbst, my sister, Shané Herbst, and my grandmother, Nellie Grobler, without your love, support, faith, sacrifices, understanding and continuous encouragement this would not be possible. Financial assistance from the Advanced Metals Initiative (AMI) of the Department of Science and Technology (DST) of South Africa, through The New Metals Development Network (NMDN) coordinated by the South African Nuclear Energy Corporation Limited (Necsa), and the University of the Free State are gratefully acknowledged. Table of contents Abbreviations and Symbols………………………………………………………………………………… V Abstract…………………………………………………………………………………………………………….. VI Opsomming……………………………………………………………………………………………….……. VIII 1 Introduction ......................................................................................... 1 1.1 History of Niobium .............................................................................................. 1 1.2 The Aim of this Study ......................................................................................... 2 2 Literature Review of Niobium ............................................................ 4 2.1 Introduction ........................................................................................................ 4 2.1.1 Properties of Niobium .................................................................................. 5 2.1.2 Uses ............................................................................................................ 8 2.2 Separation of Niobium and Tantalum………………………………………………..10 2.2.1 Marignac Process ...................................................................................... 10 2.2.2 Solvent Extraction ...................................................................................... 10 2.2.3 Current Research ...................................................................................... 11 2.3 Purification ....................................................................................................... 12 2.4 Chemistry of Niobium ....................................................................................... 13 2.4.1 Oxides ....................................................................................................... 13 2.4.2 Halides....................................................................................................... 14 2.4.3 Borides ...................................................................................................... 15 2.4.4 Carbides .................................................................................................... 15 2.4.5 Nitrides ...................................................................................................... 15 2.4.6 Water absorption ....................................................................................... 16 2.4.7 Silicates ..................................................................................................... 16 I 2.4.8 Cyclopentadienes ...................................................................................... 17 2.4.9 Phosphates ................................................................................................ 17 2.5 Niobium as Catalyst ......................................................................................... 18 2.6 β-diketone Complexes of Niobium ................................................................... 20 2.6.1 Tetrakis( β-diketonate) niobium(IV) complexes .......................................... 21 2.6.1.1 [Nb(thd) 4].............................................................................21 2.6.1.2 [Nb(hfacac)4]........................................................................22 2.6.2 Bis( β-diketonate) niobium(IV) complexes .................................................. 23 2.6.2.1 trans-[NbCl 2(thd) 2]...............................................................23 2.6.3 Mono( β-diketonate) niobium(V) complexes ............................................... 24 2.6.3.1 fac -[Nb(NCS)(Opr) 3(dbm)] and trans -[Nb (NCS) 2(OEt) 2(dbm)].............................................................24 2.6.3.2 [Nb(OEt)4(dbm)]...................................................................25 - 2.6.3.3 [NbCl 3O(ttbd) ].....................................................................26 2.6.3.4 trans-[NbCl 2(OEt)2(dbm)].....................................................26 2.6.4 Bridged niobium β-diketonate complexes .................................................. 27 2.6.4.1 [Nb 2(µ-S2)2(acac) 4] and [Nb 2(µ-S2)(acac) 4]..........................27 2.6.4.2 [Sr 2Nb 2O(thd) 3(OEt) 9(EtOH) 3] and n n [Sr 2Nb 2O(thd) 3(O Pr) 9( PrOH) 3]...........................................28 2.7 Alkoxides .......................................................................................................... 30 2.7.1 Preparation of Metal alkoxides .................................................................. 30 2.7.2 Niobium alkoxides ..................................................................................... 32 2.7.3 93 Nb NMR Studies ..................................................................................... 33 2.8 Kinetic Studies of Niobium Complexes ............................................................ 36 2.9 Conclusion ....................................................................................................... 41 3 Synthesis and Characterisation of Niobium(V) Complexes ........... 42 3.1 Introduction ...................................................................................................... 42 3.2 Nuclear Magnetic Resonance Spectroscopy (NMR) ........................................ 42 3.3 Ultraviolet-visible Spectroscopy (UV/Vis) ......................................................... 45 II 3.4 Infrared Spectroscopy (IR) ............................................................................... 45 3.5 X-Ray Diffraction (XRD) ................................................................................... 47 3.5.1 Bragg’s law ................................................................................................ 48 3.5.2 Structure factor .......................................................................................... 49 3.5.3 ‘Phase problem’ ......................................................................................... 50 3.5.3.1 Direct method......................................................................50 3.5.3.2 Patterson method................................................................50 3.5.4 Least-squares refinement .......................................................................... 51 3.6 Chemical Kinetics ............................................................................................. 51 3.6.1 Reaction rate and rate laws ....................................................................... 52 3.7 Synthesis and Spectroscopic Characterisation of Compounds ........................ 54 3.7.2 Synthetic Procedures ................................................................................ 54 3.7.2.1 Synthesis of [NbCl(acac)(OMe) 3].........................................54 3.7.2.2 Synthesis of [Nb(acac)(OEt) 2(O)] 4.......................................55 3.7.2.3 Synthesis of [NbCl(phacac)(OMe) 3] and [NbCl 2(phacac)(OMe) 2]........................................................55 3.7.2.4 Synthesis of [NbCl 4(acac)]...................................................55 3.7.2.5 Synthesis of [NbCl 4(hfacac)]................................................56 3.7.2.6 Synthesis of [NbCl(trop)(OMe) 3]..........................................56 3.7.3 Discussion ................................................................................................. 57 3.7.4 Conclusion ................................................................................................. 57 4 Crystallographic Characterisation of Niobium(V) β-diketonate Complexes .............................................................................................. 58 4.1 Introduction ...................................................................................................... 58 4.2 Experimental .................................................................................................... 59 2 4.3 Crystal Structure of [NbCl(acac-К
Load more

Recommended publications
  • Molecular Beam Epitaxy in the Lithium-Niobium-Oxygen System
    MOLECULAR BEAM EPITAXY IN THE LITHIUM-NIOBIUM-OXYGEN SYSTEM by Mario Petrucci Department of Electrical and Electronic Engineering, University College London. A thesis submitted to University College, University of London for the degree of Doctor of Philosophy. October, 1989 1 ProQuest Number: 10610929 All rights reserved INFORMATION TO ALL USERS The quality of this reproduction is dependent upon the quality of the copy submitted. In the unlikely event that the author did not send a com plete manuscript and there are missing pages, these will be noted. Also, if material had to be removed, a note will indicate the deletion. uest ProQuest 10610929 Published by ProQuest LLC(2017). Copyright of the Dissertation is held by the Author. All rights reserved. This work is protected against unauthorized copying under Title 17, United States C ode Microform Edition © ProQuest LLC. ProQuest LLC. 789 East Eisenhower Parkway P.O. Box 1346 Ann Arbor, Ml 48106- 1346 To the memory of my father, Vincenzo Petrucci. 'We work not only to produce But to give value to time." Eugene Delacroix "Oh, Mr. Scientist: you take what you see And fashion a wondrous soliloquy; But greater magic is forged in what you write: Where night becomes day and day becomes night!" 2 ABSTRACT The N b -L i-0 materials system offers an extensive combination of properties useful to integrated optics. N b ^ and L iN b 03 already have applications in waveguiding devices, such as electro-optic modulators, Fresnel lenses, and SAW transducers. In several cases, however, it would be desirable to grow these oxides on lattice-matched substrates as epitaxial thin films of controlled composition, crystallinity, and thickness: this thesis describes work aimed at achieving this goal.
    [Show full text]
  • Official Journal of the Patent Office
    ¯Öê™ëü™ü úÖµÖÖÔ»ÖµÖ úÖ ¿ÖÖÃÖúßµÖ •Ö−ÖÔ»Ö OFFICIAL JOURNAL OF THE PATENT OFFICE (SUPPLEMENT TO THE OFFICIAL JOURNAL DATED 27/03/2009) ×−ÖÖÔ´Ö−Ö ÃÖÓ. 13/2009 ¿ÖãÎú¾ÖÖ¸ ü פü−ÖÖÓú: 27/03/2009 ISSUE NO. 13/2009 FRIDAY DATE: 27/03/2009 ¯Öê™ëü™ü úÖµÖÖÔ»ÖµÖ úÖ ‹ú ¯ÖÏúÖ¿Ö−Ö PUBLICATION OF THE PATENT OFFICE The Patent Office Journal 27/03/2009 16607 CONTENTS SUBJECT PAGE NUMBER JURISDICTION : 16609-16610 PUBLICATION UNDER SECTION 43(2) IN RESPE CT : 16611-16776 OF THE GRANT (DELHI) PUBLICATION UNDER SECTION 43(2) IN RESPEC T : 16777-16779 OF THE GRANT (MUMBAI) PUBLICATION UNDER SECTION 43(2) IN RESPE CT : 16780-16788 OF THE GRANT (CHENNAI) The Patent Office Journal 27/03/2009 16608 THE PATENT OFFICE KOLKATA, 27/03/2009 Address of the Patent Offices/Jurisdictions The following are addresses of all the Patent Offices located at different places having their Territorial Jurisdiction on a Zonal basis as shown below:- 1 Office of the Controller General of Patents, 4 The Patent Office, Designs & Trade Marks, Government of India, Boudhik Sampada Bhavan, Intellectual Property Rights Building, Near Antop Hill Post Office,S.M.Road,Antop Hill, G.S.T. Road, Guindy, Mumbai – 400 037 Chennai – 600 032. Phone: (91)(22) 24123311, Phone: (91)(44) 2250 2081-84 Fax : (91)(22) 24123322 Fax : (91)(44) 2250 2066 E-mail: [email protected] E-mail: [email protected] The States of Andhra Pradesh, Karnataka, Kerala, Tamil Nadu and the Union Territories of Puducherry and Lakshadweep. 2 The Patent Office, Government of India, 5 The Patent Office (Head Office), Boudhik Sampada
    [Show full text]
  • Open Thesis.Pdf
    The Pennsylvania State University The Graduate School Department of Chemistry ALKYNYLIODONIUM SALTS IN ORGANIC SYNTHESIS. APPLICATION TOWARDS THE SYNTHESIS OF THE CORE OF (±)-HALICHLORNIE. and ATTEMPTS TOWARDS THE SYNTHESIS OF KINAMYCIN F. A Thesis in Chemistry by Angela Lyn Perkins © 2005 Angela Lyn Perkins Submitted in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy August 2005 The thesis of Angela Lyn Perkins was reviewed and approved* by the following: Ken S. Feldman Professor of Chemistry Thesis Advisor Chair of Committee Blake R. Peterson Associate Professor of Chemistry Raymond L. Funk Professor of Chemistry Squire J. Booker Assistant Professor of Biochemistry and Molecular Biology Ayusman Sen Professor of Chemistry Head of the Department of Chemistry *Signatures are on file in the Graduate School iii ABSTRACT Alkynyliodonium salts are synthetically useful intermediates that serve as electrophilic acetylene equivalents due to the electron withdrawing nature of the hypervalent iodine. In one example, reaction of an alkynyliodonium salt with soft nucleophiles via conjugate addition, followed by loss of iodobenzene, generates alkylidenecarbenes. Alkylidenecarbenes are divalent, short lived intermediates capable of participating in a various bond-forming processes depending upon the functionality present within the molecule. Due to the wide variety of possible reactions, alkylidenecarbenes are useful reactive intermediates in natural product synthesis. The application of alkynyliodonium salts to generate alkylidenecarbenes is described in the first part of this thesis. Chapter 1 discusses the formation of alkynyliodonium salts and their application towards the generation of alkylidenecarbenes. The total synthesis of radermachol, a natural product target, was examined utilizing an alkylidenecarbene addition to a double bond as a key step.
    [Show full text]
  • The Effect of Stress on the Low-Temperature Oxidation of Niobium Lawrence John Weirick Iowa State University
    Iowa State University Capstones, Theses and Retrospective Theses and Dissertations Dissertations 1969 The effect of stress on the low-temperature oxidation of niobium Lawrence John Weirick Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/rtd Part of the Metallurgy Commons Recommended Citation Weirick, Lawrence John, "The effect of stress on the low-temperature oxidation of niobium " (1969). Retrospective Theses and Dissertations. 3617. https://lib.dr.iastate.edu/rtd/3617 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Retrospective Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. This dissertation has been microfihned exactly as received 69-20,683 WEIRICK, Lawrence John, 1941- THE EFFECT OF STRESS ON THE LOW- TEMPERATURE OXIDATION OF NIOBIUM. Iowa State University, Ph.D., 1969 Engineering, metallurgy University Microfilms, Inc., Ann Arbor, Michigan THE EFFECT OF STRESS ON THE LOW-TEMPERATURE OXIDATION OF NIOBIUM by Lawrence John Weirick A Dissertation Submitted to the Graduate Faculty in Partial Fulfillment of The Requirements for the Degree of DOCTOR OF PHILOSOPHY Major Subject: Metallurgy Approved: Signature was redacted for privacy. In Charge of Major Work Signature was redacted for privacy. Signature was redacted for privacy. uate
    [Show full text]
  • EELS Investigations of Different Niobium Oxide Phases
    Microsc. Microanal. 12, 416–423, 2006 / DOI: 10.1017 S1431927606060521 Microscopy AND Microanalysis © MICROSCOPY SOCIETY OF AMERICA 2006 EELS Investigations of Different Niobium Oxide Phases D. Bach,1,* H. Störmer,1 R. Schneider,1 D. Gerthsen,1 and J. Verbeeck2 1Laboratorium für Elektronenmikroskopie, Universität Karlsruhe (TH), D-76128 Karlsruhe, Germany 2Electron Microscopy for Materials Research (EMAT), University of Antwerp, Groenenborgerlaan 171, 2020 Antwerp, Belgium Abstract: Electron energy loss spectra in conjunction with near-edge fine structures of purely stoichiometric niobium monoxide ~NbO! and niobium pentoxide ~Nb2O5! reference materials were recorded. The structures of the niobium oxide reference materials were checked by selected area electron diffraction to ensure a proper assignment of the fine structures. NbO and Nb2O5 show clearly different energy loss near-edge fine structures of the Nb-M4,5 and -M2,3 edges and of the O-K edge, reflecting the specific local environments of the ionized atoms. To distinguish the two oxides in a quantitative manner, the intensities under the Nb-M4,5 as well as Nb-M2,3 edges and the O-K edge were measured and their ratios calculated. k-factors were also derived from these measurements. Key words: niobium monoxide, niobium pentoxide, EELS, ELNES, quantification, stoichiometry INTRODUCTION nanoscale dielectric oxide layers in capacitor structures is essential. Such studies are of importance to understand the mechanisms of leakage currents, which might be due to Niobium and niobium-based compounds have been stud- n-type semiconducting behavior of parts of the dielectric ied for several decades. They find many technological appli- oxide layer as a result of oxygen deficiencies.
    [Show full text]
  • Transition Metal Oxides
    . _ ^ ^ „ OCT 14 1975 175118 '-cy NSRDS-NBS 49 Transition Metal Oxides U.S. DEPARTMENT OF COMMERCE/National Bureau of Standards NSRDS Ice dat* Crystal Chemistry, Phase Transition and Related Aspects NATIONAL BUREAU OF STANDARDS The National Bureau of Standards 1 was established by an act of Congress March 3, 1901. The Bureau’s overall goal is to strengthen and advance the Nation’s science and technology and facilitate their effective application for public benefit. To this end, the Bureau conducts research and provides: (1) a basis for the Nation’s physical measurement system, (2) scientific and technological services for industry and government, (3) a technical basis for equity in trade, and (4) technical services to promote public safety. The Bureau consists of the Institute for Basic Standards, the Institute for Materials Research, the Institute for Applied Technology, the Institute for Computer Sciences and Technology, and the Office for Information Programs. THE INSTITUTE FOR BASIC STANDARDS provides the central basis within the United States of a complete and consistent system of physical measurement; coordinates that system with measurement systems of other nations; and furnishes essential services leading to accurate and uniform physical measurements throughout the Nation’s scientific community, industry, and commerce. The Institute consists of a Center for Radiation Research, an Office of Meas- urement Services and the following divisions: Applied Mathematics — Electricity — Mechanics — Heat — Optical Physics — Nuclear Sciences 2 — Applied Radiation 2 — Quantum Electronics 3 — Electromagnetics 3 — Time 3 3 3 and Frequency — Laboratory Astrophysics — Cryogenics . THE INSTITUTE FOR MATERIALS RESEARCH conducts materials research leading to improved methods of measurement, standards, and data on the properties of well-characterized materials needed by industry, commerce, educational institutions, and Government; provides advisory and research services to other Government agencies; and develops, produces, and distributes standard reference materials.
    [Show full text]
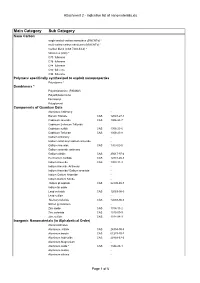
  • Attachment 2 - Indicative List of Nanomaterials.Xls
    Attachment 2 - Indicative list of nanomaterials.xls Main Category Sub Category Nano Carbon single-walled carbon nanotubes (SWCNTs) * multi-walled carbon nanotubes (MWCNTs) * Carbon black (CAS 7440-44-0) * fullerenes (C60) * C70 fullerene C76 fullerene C84 fullerene C90 fullerene C94 fullerene Polymers specifically synthesized to exploit nanoproperties Polystyrene * Dendrimers * Polyamidoamine (PAMAM) Polyethylene imine Ferrocenyl Polyglycerol Components of Quantum Dots Aluminum Antinomy - Barium Titanate CAS 12047-27-7 Cadmium selenide CAS 1306-24-7 Cadmium Selenium Telluride Cadmium sulfide CAS 1306-23-6 Cadmium Telluride CAS 1306-25-8 Gallium Antimony - Gallium antimony/ Gallium arsenide - Gallium Arsenide CAS 1303-00-0 Gallium arsenide antimony Gallium nitride CAS 25617-97-4 Germanium carbide CAS 12334-26-8 Indium Arsenide CAS 1303-11-3 Indium Arsenide Antimony - Indium Arsenide/ Gallium arsenide - Indium Gallium Arsenide - Indium Gallium Nitride - Indium phosphide CAS 22398-80-7 Indium tin oxide - Lead selenide CAS 12069-00-0 Lead sulfide - Mercury telluride CAS 12068-90-5 Silicon germanium - Zinc oxide CAS 1314-13-2 Zinc selenide CAS 1315-09-9 Zinc sulfide CAS 1314-98-3 Inorganic Nanomaterials (in Alphabetical Order) Aluminosilicates - Aluminum nitride CAS 24304-00-5 Aluminum borate CAS 61279-70-7 Aluminum hydroxide CAS 20768-67-6 Aluminum Magnesium - Aluminum oxide * CAS 1344-28-1 Aluminum oxides - Aluminum silicate - Page 1 of 6 Attachment 2 - Indicative list of nanomaterials.xls Main Category Sub Category Aluminum Titanium Oxide
    [Show full text]
  • Highly-Correlated Electron Behavior in Niobium and Niobium Compound Thin Films
    W&M ScholarWorks Dissertations, Theses, and Masters Projects Theses, Dissertations, & Master Projects Winter 2017 Highly-Correlated Electron Behavior in Niobium and Niobium Compound Thin Films Melissa R. Beebe College of William and Mary, [email protected] Follow this and additional works at: https://scholarworks.wm.edu/etd Part of the Physics Commons Recommended Citation Beebe, Melissa R., "Highly-Correlated Electron Behavior in Niobium and Niobium Compound Thin Films" (2017). Dissertations, Theses, and Masters Projects. Paper 1499450045. http://doi.org/10.21220/S2K95B This Dissertation is brought to you for free and open access by the Theses, Dissertations, & Master Projects at W&M ScholarWorks. It has been accepted for inclusion in Dissertations, Theses, and Masters Projects by an authorized administrator of W&M ScholarWorks. For more information, please contact [email protected]. Highly-Correlated Electron Behavior in Niobium and Niobium Compound Thin Films Melissa R. Beebe Chesapeake, Virginia Master of Science, College of William & Mary, 2014 Bachelor of Science, Old Dominion University, 2012 Bachelor of Arts, Old Dominion University, 2012 ADissertationpresentedtotheGraduateFaculty of The College of William & Mary in Candidacy for the Degree of Doctor of Philosophy Department of Physics College of William & Mary May 2017 c 2017 Melissa R. Beebe All rights reserved. ABSTRACT Electron correlations are the root of many interesting phenomena in materials, including phase transitions such as superconductivity and insulator-to-metal transitions, which are of great interest both for scientific understanding and for many applications. Such phase transitions can often be tailored in thin films, in which the geometry of the material is limited in one dimension.
    [Show full text]
  • Aec-Nasa Tech Brief
    March 1967 Brief 67-10062 O AEC-NASA TECH BRIEF YES AEC-NASA Tech Briefs describe innovations resulting from the research and development program of the U.S. AEC or from AEC-NASA interagency efforts. They are issued to encourage commercial application. Tech Briefs are published by NASA and may be purchased, at 15 cents each, from the Clearinghouse for Federal Scientific and Technical Information, Springfield, Virginia 22151. Recommended Values of the Thermophysical Properties of Eight Alloys, Their Major Constituents and Oxides Technical personnel who design, fabricate, and of the materials studied. An effort was made to fill in manufacture products, components, processes, and these gaps wherever feasible through theoretical or systems which involve extreme temperature environ- semiempirical considerations. Some of the data were ments such as cryogenic and high temperatures to and also extrapolated whenever it was believed justifiable beyond the melting range require the knowledge of the within the limits of tolerances set for most engineering thermophysical properties of the basic alloys, their applications. constituents and oxides that would be utilized. A Note: single reference work has been prepared that provides Copies of the report are available from: in tabular and graphical form the . recommended Technology Utilization Officer properties of specific heat, thermal conductivity, vis- AEC-NASA Space Nuclear Propulsion cosity, thermal emissivity, thermal diffusivity, density, Office and surface tension of aluminum, aluminum alloys, U.S. Atomic Energy Commission inconel, titanium, beryllium and stainless steel. Washington, D.C. 20545 The data are contained in the technical report: Reference: B67-10062 "Recommended Values of the Thermophysical Prop- erties of Eight Alloys, Major Constituents and their Patent status: Oxides," edited by Y.S.
    [Show full text]
  • Niobium Oxide Catalysts As Emerging Material for Textile Wastewater Reuse: Photocatalytic Decolorization of Azo Dyes
    catalysts Article Niobium Oxide Catalysts as Emerging Material for Textile Wastewater Reuse: Photocatalytic Decolorization of Azo Dyes Alexsandro Jhones dos Santos 1 , Luana Márcia Bezerra Batista 2, Carlos Alberto Martínez-Huitle 1,*, Ana Paula de Melo Alves 3,* and Sergi Garcia-Segura 4,* 1 Laboratório de Eletroquímica Ambiental e Aplicada (LEAA), Institute of Chemistry, Federal University of Rio Grande do Norte, Lagoa Nova, 59078-970 Natal, Brazil; [email protected] 2 Instituto Federal de Pernambuco, Campus Afogados da Ingazeira, Rua Edson Barbosa de Araújo, s/n, Bairro Manoela Valadares, 56800-000 Afogados da Ingazeira-PE, Brazil; [email protected] 3 Laboratório de Combustíveis e Materiais (LACOM), Department of Chemistry, Federal University of Paraíba, Campus I—Lot. Cidade Universitária, 58051-900 João Pessoa, Brazil 4 Nanosystems Engineering Research Center for Nanotechnology-Enabled Water Treatment, School of Sustainable Engineering and the Built Environment, Arizona State University, Tempe, AZ 85287-3005, USA * Correspondence: [email protected] (C.A.M.-H.); [email protected] (A.P.d.M.A.); [email protected] (S.G.-S.) Received: 2 December 2019; Accepted: 12 December 2019; Published: 14 December 2019 Abstract: Niobium-based metal oxides are emerging semiconductor materials with barely explored properties for photocatalytic wastewater remediation. Brazil possesses the greatest reserves of niobium worldwide, being a natural resource that is barely exploited. Environmental applications of solar active niobium photocatalysts can provide opportunities in the developing areas of Northeast Brazil, which receives over 22 MJ m2 of natural sunlight irradiation annually. The application of photocatalytic treatment could incentivize water reuse practices in small and mid-sized textile businesses in the region.
    [Show full text]
  • NBO 2016 – 2008 References Compiled by Ariel Andrea on 8/31/2018
    NBO 2016 – 2008 references Compiled by Ariel Andrea on 8/31/2018 Aal, S. A. Reactivity of boron- and nitrogen-doped carbon nanotubes functionalized by (Pt, Eu) atoms toward O-2 and CO: A density functional study International Journal of Modern Physics C, (27) 2016. 10.1142/s0129183116500753 Abbat, S.; Bharatam, P. V. Electronic structure and conformational analysis of P218: An antimalarial drug candidate International Journal of Quantum Chemistry, (116): 1362-1369. 2016. 10.1002/qua.25189 Abbenseth, J.; Finger, M.; Wurtele, C.; Kasanmascheff, M.; Schneider, S. Coupling of terminal iridium nitrido complexes Inorganic Chemistry Frontiers, (3): 469-477. 2016. 10.1039/c5qi00267b Abboud, J. L. M.; Alkorta, I.; Davalos, J. Z.; Koppel, I. A.; Koppel, I.; Lenoir, D.; Martinez, S.; Mishima, M. The Thermodynamic Stability of Adamantylideneadamantane and Its Proton- and Electron-Exchanges. Comparison with Simple Alkenes Bulletin of the Chemical Society of Japan, (89): 762-769. 2016. 10.1246/bcsj.20160026 Abdalrazaq, S. M.; Cabir, B.; Gumus, S.; Agirtas, M. S. Synthesis of metallophthalocyanines with four oxy-2,2-diphenylacetic acid substituents and their structural and electronic properties Heterocyclic Communications, (22): 275-280. 2016. 10.1515/hc-2016-0120 Abdelmoulahi, H.; Ghalla, H.; Nasr, S.; Bahri, M.; Bellissent-Funel, M. C. Hydrogen-bond network in liquid ethylene glycol as studied by neutron scattering and DFT calculations Journal of Molecular Liquids, (220): 527-539. 2016. 10.1016/j.molliq.2016.04.111 Abdelmoulahi, H.; Ghalla, H.; Nasr, S.; Darpentigny, J.; Bellissent-Funel, M. C. Intermolecular associations in an equimolar formamide-water solution based on neutron scattering and DFT calculations Journal of Chemical Physics, (145) 2016.
    [Show full text]
  • 61581939.Pdf
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Cork Open Research Archive Title Asymmetric oxidation of sulfides Author(s) O'Mahony, Graham E.; Ford, Alan; Maguire, Anita R. Publication date 2012-10-16 Original citation O'Mahony, G. E., Ford, A. and Maguire, A. R. (2013) 'Asymmetric oxidation of sulfides'. Journal of Sulfur Chemistry, 34(3), pp. 301-341. http://dx.doi.org/10.1080/17415993.2012.725247 Type of publication Article (peer-reviewed) Link to publisher's http://dx.doi.org/10.1080/17415993.2012.725247 version Access to the full text of the published version may require a subscription. Rights © 2013 Taylor and Francis Group, LLC. This is a Submitted Manuscript of an article published by Taylor & Francis in Journal of Sulfur Chemistry on 16 Oct 2012, available online: http://www.tandfonline.com/10.1080/17415993.2012.725247. Item downloaded http://hdl.handle.net/10468/2996 from Downloaded on 2017-02-12T09:56:30Z Asymmetric Oxidation of Sulfides Graham E. O’Mahonya, Alan Forda and Anita R. Maguireb* aDepartment of Chemistry, Analytical and Biological Chemistry Research Facility, University College Cork, Cork, Ireland. bDepartment of Chemistry and School of Pharmacy, Analytical and Biological Chemistry Research Facility, University College Cork, Cork, Ireland. [email protected] Abstract This review discusses synthesis of enantiopure sulfoxides through the asymmetric oxidation of prochiral sulfides. The use of metal complexes to promote asymmetric sulfoxidation is described in detail, with a particular emphasis on the synthesis of biologically active sulfoxides. The use of non-metal based systems, such as oxaziridines, chiral hydroperoxides and peracids, as well as biologically-catalyzed sulfoxidations is also examined.
    [Show full text]