NEMS-Based Infrared Metamaterial Via Tuning Nanocantilevers Within Complementary Split Ring Resonators Qiugu Wang, Depeng Mao, Peng Liu, Thomas Koschny, Costas M
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Bending Back Light the Science of Negative Index Materials
Bending Back Light The Science of Negative Index Materials Costas M. Soukoulis Using the right type of man-made materials, light can be made to bend, or refract, backwards. After years of painstakingly developing and testing the necessary materials, hen light enters specially engineered materials scientists are now called metamaterials, it takes a sharp turn to the looking to translate W left—a negative turn—bending in the opposite direction of light going through natural materials. Scientists fre- negative refraction into quently refer to these unique synthetic materials as left-handed positive applications materials (LHMs) or negative index materials (NIMs). Since the first demonstration of an artificial negative refrac- such as sub-wavelength, tive index material in 2000, metamaterials have drawn consid- high-resolution erable attention from scientists because of their broad range of potential applications. For example, they may one day lead to imaging across the the development of a flat superlens that operates in the visible electromagnetic spectrum, which would offer superior resolution over conven- tional technology and provide images much smaller than one spectrum. wavelength of light. Photo by Timothy Finegan 16 | OPN June 2006 1047-6938/06/06/0016/6-$15.00 ©OSA Costas Soukoulis examines one of the photonic crystals that was construct- ed to observe negative refraction and superlensing in the microwave region of the electromagnetic spectrum. Photo by Dennis Sailsbury, Ames Lab They also have many promising applications for defense magnetic responses in materials naturally occur over different and security. Because NIMs can match the impedance, or the frequency ranges, making their overlap unlikely. -

A Policy for Success
bponline.amcham.gr MAY-JUNE 2014 Vol. XIII | No. 72 Thought Leaders Golden Bullets in Technolgy BUSINESS MATTERS— JIM DAVIS OF NEW BALANCE ▼ PANAGIOTIS G. MIHALOS, SECRETARY GENERAL, MFA ▼ GOOGLE, THE INTERNET, AND IMPACTING SOCIETY ▼ PLUS BIZ BUZZ TRENDS & TRADE MAKERS VIEWPOINT MetLife— AMERICAN-HELLENIC A Policy For Success CHAMBER OF COMMERCE www.amcham.gr Dimitris Mazarakis Vice Chairman BoD & Managing Director, MetLife Register Now Greek Investment June 11-12, 2014 Forum The Athens Exchange and the AEGEAN AIRLINES American-Hellenic Chamber of Commerce ALPHA BANK are pleased to invite you to this year’s ATTICA BANK Investment Forum: CORINTH PIPEWORKS ELLAKTOR Participants: GR for Growth EUROBANK EUROBANK PROPERTIES JUNE 11-12, 2014 FOLLI FOLLIE GROUP Harmonie Club, 4 East 60th St, GEK TERNA New York, NY 10022 GR. SARANTIS HELLENIC EXCHANGES The Forum will bring together HELLENIC PETROLEUM key government of cials and INTRALOT leading Greek and U.S. LAMDA DEVELOPMENT business leaders to explore Greece’s MARFIN INVESTMENT GROUP improving investment climate, METKA key privatization initiatives MOTOR OIL MYTILINEOS and investment opportunities. NATIONAL BANK of GREECE Institutional investors OPAP will also have the opportunity to meet PIRAEUS BANK with senior executives PLAISIO of Greece’s leading listed companies. TERNA ENERGY THRACE PLASTICS The Forum will take place on June 11. TITAN One-on-one investor meetings will take HELLENIC REPUBLIC ASSET place on June 11-12. DEVELOPMENT FUND Gold sponsors: Silver sponsors: Hellenic American -

Negative-Index Materials: New Frontiers in Optics**
REVIEW DOI: 10.1002/adma.200600106 Negative-Index Materials: New Frontiers in Optics** By Costas M. Soukoulis,* Maria Kafesaki, and Eleftherios N. Economou A lot of recent interest has been focused on a new class of materials, the so-called left-handed materials (LHMs) or negative-index materials, which exhibit highly unusual electromagnetic properties and hold prom- ise for new device applications. These materials do not exist in nature and can only be fabricated artificially; for this reason, they are called meta- materials. Their unique properties are not determined by the fundamental physical properties of their constituents, but rather by the shape and distribution of the specific patterns included in them. Metamaterials can be designed to exhibit both electric and magnetic resonances that can be separately tuned to occur in frequency bands from megahertz to terahertz frequencies, and hope- fully to the visible region of the electromagnetic spectrum. This article presents a short history of the field, describes the underlying physics, and reviews the experimental and theoretical status of the field at present. Many interesting questions on how to fabricate more isotropic LHMs, on how to push the operational frequency to optical wavelengths, how to reduce the losses, and how to incorporate active or nonlinear materials in LHMs remain to be explored further. – 1. Introduction [*] Prof. C. M. Soukoulis Department of Physics and Ames Laboratory Iowa State University 1.1. History of Negative-Index Materials (or Left-Handed Ames, IA 50011(USA) E-mail: [email protected] Materials) Prof. C. M. Soukoulis, Dr. M. Kafesaki Foundation for Research and Technology, Hellas (FORTH) Electromagnetic metamaterials are artificially structured Institute of Electronic Structure and Laser (IESL) media with unique and distinct properties that are not ob- P.O. -

Union Radio-Scientifique Internationale
Appendix 2 – page 1 1. NAME OF CANDIDATE: Pendry, John, Brian Last, First, Middle PRESENT OCCUPATION: Chair in Theoretical Solid State Physics, Imperial College London Position, Organization BUSINESS ADDRESS: Room 808, Blackett, Imperial College London, South Kensington Campus, London SW7 2AZ, United Kingdom HOME ADDRESS: Metchley, Knipp Hill, Cobham, Surrey, KT11 2PE, United Kingdom BIRTHDATE: 4th July, 1943 NATIONALITY: UK SEX: male - female (Underline the appropriate) 2. EDUCATION (Honorary degrees denoted by H) Educational Institution Location Degrees Year University of Cambridge Cambridge, UK BA Physics 1965 University of Cambridge Cambridge, UK MA Physics 1969 University of Cambridge Cambridge, UK PhD Physics 1969 Universität Erlangen Nürnberg, Germany Doctorate H 2009 Duke University USA Doctor of Science H 2010 Hong Kong Baptist University Hong Kong Doctor of Science H 2010 3. PROPOSED CITATION (not more than thirty words) For work on electromagnetic and optical metamaterials, the perfect lens and transformation optics 4. NOMINATOR: Dr Constantinos Constantinou, Chair, UK URSI Panel ADDRESS: School of Electronic, Electrical and Computer Engineering, The University of Birmingham, Edgbaston, Birmingham, B15 2TT, United Kingdom PHONE: +44-121-414-4303 FAX: +44-121-414-4291 E-MAIL : [email protected] Appendix 2 – page 2 5. PROFESSIONAL HISTORY - Present position first. Limit copy to this page. From (year) to (year) Name of Company/Institution Position and Responsibilities 1981 present Imperial College London, UK Professor -

SPPM2021 Online International Conference
ONLINE INTERNATIONAL CONFERENCE ORGANISERS On behalf of the Organising Committee we take great pleasure in welcoming you for the 1st edition of the “SPPM2021” Online Conference (Spintronics, Photonics, Phononics & Magneto- Optics): June 10, 2021. The SPPM2021 Online conference will present the most recent advances in fundamental research and related applications in Photonics, Phononics, Spintronics or Magneto-Optics. This online event aim is to bring together top researchers and future leaders encouraging interactions between students, young speakers, and senior figures in the field. The topics will cover the experimental and theoretical aspects of light interaction with nanoscale objects and nanostructured materials. SPPM2021 will also explore different cutting edge research topics where phonons play a central role such as quantum photonics, nanoscale thermal transport, topological phononics, nanophononics and optomechanics. We are indebted to IFIMAC/UAM (Spain) for their help and financial support. We also would like to thank all the speakers and participants that join us this year. Hope to see you in-person in Bilbao (Spain) for the 3PM2021 International Conference organised within Imaginenano2021 (www.imaginenano.com/2021/PPM2021.php). rganising ommittee 2021 International Online Conference 2 Organising Committee Antonio Correia (Phantoms Foundation, Spain) - Chairperson Francisco José García Vidal (UAM / IFIMAC, Spain) Alejandro Martinez (Nanophotonics Technology Center, Spain) Lluis F. Marsal (Universitat Rovira i Virgili, Spain) -

LASER-FOCUSED Grant Luhmann Laura Millsaps Breehan Gerlemanlucchesi Kerry Gibson Steve Karsjen Educating Andtrainingtomorrow’S Scientifictalent
Science & Technology at the Ames Laboratory 2014 Issue 2 NEW MATERIALS VIA 3D PRINTING Boosting NMR sensitivity with microwaves Ionic liquids for rare-earth recovery Shielding sensitive instruments LASER-FOCUSED CMI, Year One Listening to Industry PA8GE 4 Awards Schwartz 10 Reflects SIF NEARING COMPLETION 6 Learning the 12 Language of Cell Life Anja Mudring Ionic Liquids, High Hopes 14 Ames Laboratory’s16 3D Printing Technology Education Contents 19 Steve Karsjen: Public Affairs Director Copyright 2014 by the Ames Laboratory. All rights Editor, Inquiry Kerry Gibson: Editor reserved. For additional information about the Ames Ames Laboratory Laboratory or topics covered in this publication, 111 TASF Breehan Gerleman Lucchesi: Contributing Editor please contact: Ames, Iowa 50011-3020 Laura Millsaps: Contributing Editor 515-294-9557 Grant Luhmann: Art Director www.ameslab.gov The Ames Laboratory is a U.S. Department of Energy national laboratory seeking solutions to energy-related Inquiry is published biannually by the Ames problems through the exploration of chemical, engineering, materials and mathematical sciences, and physics. Laboratory Office of Public Affairs. Iowa Established in the 1940s with the successful development of the most efficient process to produce high-purity State University operates the Laboratory uranium metal for atomic energy, Ames Lab now pursues much broader priorities than the materials research that for the U.S. Department of Energy under has given the Lab international credibility. Responding to issues of national concern, Ames Laboratory scientists contract DE AC02 07CH11358. are actively involved in innovative research, science education programs, the development of applied technologies and the quick transfer of such technologies to industry. -

Manolis Antonoyiannakis Editor, Physical Review Le�Ers Ling Miao (缪凌) Editor, Physical Review X
Editors’ Session Manolis Antonoyiannakis Editor, Physical Review Le;ers Ling Miao (缪凌) Editor, Physical Review X Outline • Physical Review X • The editors’ point of view: • Editors’ role and challenges • What papers we are looking for • Some key quesHons in the field • Editorial standards: do they evolve? • Top-quality papers: fast-tracking, highlighHng • Unsuitable papers: editorial rejecHon • Impact stasHcs Why PR High Profile Gold Open Access Commercial Society NJP Nature Physics (good quality, well regarded) Nature Materials PRL P Nature Photonics R Nature AIP Advances Nanotechnology (For publicaon: only technical correctness) Physical Review X • all areas of physics • highly selective standards: eXceptional in originality, quality & substance, significance • eXpress editorial/review process • well-informed, responsible editorial judgment • no length limit • online only; integrated multimedia • eXpanded access h;p://prx.aps.org Highlighted in Physics Today Physical Review X Editorial Board Broad, International, Distinguished Marcela Carena, Theoretical particle physics Fermilab/University of Chicago To Learn More Visit PRX’s Website at http://prx.aps.org The editors and the Editorial Board invite you to submit your eXceptional work to PRX The APS Editorial Office • Editor in Chief : Research areas: Gene D. Sprouse Nuclear Physics Atomic Physics Stony Brook Univ. • In-house editors: 42 (predominantly for PRL, PRB) • Remote editors (mostly acHve researchers): 61 PRA, PRC, PRD, PRE, and RMP • Technical supporHng staff: 100 37,000 papers A -
E-Mail: [email protected] , Phone Number: 2810391128
Aggelos Xomalis - Curriculum Vitae Personal data: Name: Aggelos Xomalis Nationality: Greek Home address: Mixelidaki 21, Heraklion, Crete Greece Contact info: Address: Institute of Electronic Structure and Laser, Foundation for Research and Technology - Hellas, P.O. Box 1385, 71110 Heraklion, Crete E-mail: [email protected] , phone number: 2810391128 Current position: MSc Candidate Dept. of Materials Science and Technology, Univ. of Crete / Research Assistant at IESL-FORTH Education: 2013: Bachelor: Department of Materials Science and Technology, University of Crete, Greece. 2013-…: Master studies: Department of Materials Science and Technology, University of Crete, Greece. Experience: 2011-12: 3 months work experience in the microelectronics lab. I was involved in: Construction and characterization of pn diode-Construction of thin films with dc magnetron sputtering. 2010-2011: 3 months work experience in the soft matter lab. I was involved in: Synthesis and characterization on polymeric materials (styrene). 01/02/2013-01/08/2013: Undergraduate research assistant at Non-linear lithography lab at the IESL-FORTH. 2012-13: Carrying out a project concerning the negative index materials, under the supervision of Professor Maria Kafesaki (Associate Professor at the Department of Material Science and Technology) - Training in non-linear lithography with the team of Dr. Maria Farsari at the IESL-FORTH. Conference: June 9-11, 2011: Participation on Wave-Pro symposium, on the occasion of Costas Soukoulis 60th birthday, Crete, Greece. School: June 17-21, 2013: EUPROMETA – European Doctoral Programmes on Metamaterials: 22nd school, Glasgow, Scotland, UK July 15-19, 2013: “The Onassis Foundation Science Lecture Series’’. The 2013 Lectures in Physics and Chemistry: Nanoscience and Nanotechnology, Heraklion, Crete Computer and Language skills: -Linux/ UNIX, FORTRAN 77, AUTOCAD, Control and Automation Metering Systems, Microsoft office, CST microwave studio. -

Page 1 JB PENDRY - CV & PUBLICATION LIST
J.B. PENDRY - CURRICULUM VITAE at 2 January 2017 Address: Department of Physics, Imperial College London, Prince Consort Road, London SW7 2AZ, UK telephone: 020-7594-7606 email: [email protected] Date of Birth: 4th July, 1943 Degrees: 1965 BA, Cantab (Physics) 1969 MA, PhD,Cantab (Solid State Theory) 1962-65 Scholar of Downing College, Cambridge 1965-66 Part III Mathematics - postgraduate course 1966-69 Research student, Cavendish Laboratory, Cambridge 1969-73 Research Fellowship in Physics, Downing College, Cambridge 1969-71 ICI post-doctoral Fellow 1972-73 Member of Technical Staff in the Theoretical Physics Department, Bell Laboratories, Murray Hill, USA 1973-75 Senior Assistant in Research, Cavendish Laboratory, Cambridge 1973-75 Fellow in Physics and Praelector, Downing College 1975-81 Senior Principal Scientific Officer: Head of Theory Group, SERC Daresbury Laboratory 1981- Professor of Theoretical Solid State Physics, Imperial College of Science and Technology, and Head of the Condensed Matter Theory Group 1983-85 Head of Experimental Solid State Physics Group 1984 FRS 1984 F. Inst. P. 1984-92 Associate Head of Physics Department 1992-93 Member, SERC Science Board, SERC Nuclear Physics Board 1992-94 Member of Council, Royal Society. 1993-96 Dean, Royal College of Science 1996-2002 Editor, Proceedings A of the Royal Society 1996-97 Leverhulme Trust Senior Research Fellowship 1997-1998 EPSRC Senior Research 5-Year Fellowship (resigned April 1998) 1998-2001 Head of Physics Department, Imperial College London 1998-2002 Member -

Near Infrared and Optical Beam Steering and Frequency Splitting In
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Digital Repository @ Iowa State University Ames Laboratory Accepted Manuscripts Ames Laboratory 9-28-2017 Near infrared and optical beam steering and frequency splitting in air holes-in-silicon inverse photonic crystals Anna Tasolamprou Foundation for Research and Technology - Hellas Thomas Koschny Iowa State University and Ames Laboratory Maria Kafesaki Foundation for Research and Technology - Hellas and University of Crete Costas Soukoulis Ames Laboratory and Foundation for Research and Technology - Hellas Follow this and additional works at: http://lib.dr.iastate.edu/ameslab_manuscripts Part of the Condensed Matter Physics Commons, and the Semiconductor and Optical Materials Commons Recommended Citation Tasolamprou, Anna; Koschny, Thomas; Kafesaki, Maria; and Soukoulis, Costas, "Near infrared and optical beam steering and frequency splitting in air holes-in-silicon inverse photonic crystals" (2017). Ames Laboratory Accepted Manuscripts. 27. http://lib.dr.iastate.edu/ameslab_manuscripts/27 This Article is brought to you for free and open access by the Ames Laboratory at Iowa State University Digital Repository. It has been accepted for inclusion in Ames Laboratory Accepted Manuscripts by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. Near infrared and optical beam steering and frequency splitting in air holes-in-silicon inverse photonic crystals Abstract We present the design of a dielectric inverse photonic crystal structure that couples line-defect waveguide propagating modes into highly directional beams of controllable directionality. The trs ucture utilizes a triangular lattice made of air holes drilled in an infinitely thick Si slab, and it is designed for operation in the near-infrared and optical regime. -

Ames Lab Physicist Wins European Union's Highest Science Prize 9 December 2005
Ames Lab physicist wins European Union's highest science prize 9 December 2005 Costas Soukoulis leads team that will share portion "Our EXEL team was able to demonstrate the of 1 million euro Descartes Prizes experimental reality of LHMs and their consistency Costas Soukoulis, a senior physicist at the U.S. with the laws of physics," said Soukoulis. "This Department of Energy's Ames Laboratory and an realization opened up the possibility of Iowa State University Distinguished Professor of unprecedented applications and devices." The physics and astronomy, coordinates the research team has already shown how the ability to focus team that has won the Descartes Prize for radio waves could lead to smaller, better- Excellence in Scientific Collaborative Research, performing magnetic resonance imaging machines the European Union's highest honor in the field of for medical and biomedical diagnostics. Numerous science. He and his collaborators received the applications in the cellular communications industry prestigious award for creating a novel class of are also envisioned, including antennas and artificial metamaterials called left-handed waveguides that are 100 times smaller and much materials, or LHMs, which exhibit fascinating lighter than those of today. Even slight properties that cannot be found in naturally improvements to these types of devices can make occurring materials. a significant financial impact. LHMs exhibit negative refraction, bending light in Ames Laboratory Director Tom Barton praised the the opposite direction to that seen in natural work of Soukoulis and the EXEL team, saying, "It materials. They can be fabricated to have zero probably would be difficult to overstate the potential reflectance for all angles hit by incoming importance of this historic scientific achievement to electromagnetic waves. -
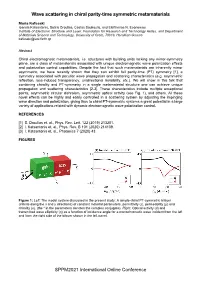
Wave Scattering in Chiral Parity-Time Symmetric Metamaterials
Wave scattering in chiral parity-time symmetric metamaterials Maria Kafesaki Ioannis Katsantonis, Sotiris Droulias, Costas Soukoulis, and Eleftherios N. Economou Institute of Electronic Structure and Laser, Foundation for Research and Technology Hellas, and Department of Materials Science and Technology, University of Crete, 70013, Heraklion Greece [email protected] Abstract Chiral electromagnetic metamaterials, i.e. structures with building units lacking any mirror-symmetry plane, are a class of metamaterials associated with unique electromagnetic wave polarization effects and polarization control capabilities. Despite the fact that such metamaterials are inherently mirror asymmetric, we have recently shown that they can exhibit full parity-time (PT) symmetry [1], a symmetry associated with peculiar wave propagation and scattering characteristics (e.g. asymmetric reflection, loss-induced transparency, unidirectional invisibility, etc.). We will show in this talk that combining chirality and PT-symmetry in a single metamaterial structure one can achieve unique propagation and scattering characteristics [2-3]. These characteristics include multiple exceptional points, asymmetric circular dichroism, asymmetric optical activity (see Fig. 1), and others. All these novel effects can be highly and easily controlled in a scattering system by adjusting the impinging wave direction and polarization, giving thus to chiral PT-symmetric systems a great potential in a large variety of applications related with dynamic electromagnetic wave polarization control. REFERENCES [1] S. Droulias et. al., Phys. Rev. Lett. 122 (2019) 213201. [2] I. Katsantonis et. al., Phys. Rev. B 101 (2020) 214109. [3] I. Katsantonis et. al., Photonics 7 (2020) 43. FIGURES Figure 1: Left: The model system discussed in the present study: A simple chiral PT-symmetric bilayer (infinite along the x and y directions) of constant material parameters, permittivity (ε), permeability (μ) and chirality (κ).