Passive Tomography of Turbulence Strength
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Israel: Growing Pains at 60
Viewpoints Special Edition Israel: Growing Pains at 60 The Middle East Institute Washington, DC Middle East Institute The mission of the Middle East Institute is to promote knowledge of the Middle East in Amer- ica and strengthen understanding of the United States by the people and governments of the region. For more than 60 years, MEI has dealt with the momentous events in the Middle East — from the birth of the state of Israel to the invasion of Iraq. Today, MEI is a foremost authority on contemporary Middle East issues. It pro- vides a vital forum for honest and open debate that attracts politicians, scholars, government officials, and policy experts from the US, Asia, Europe, and the Middle East. MEI enjoys wide access to political and business leaders in countries throughout the region. Along with information exchanges, facilities for research, objective analysis, and thoughtful commentary, MEI’s programs and publications help counter simplistic notions about the Middle East and America. We are at the forefront of private sector public diplomacy. Viewpoints are another MEI service to audiences interested in learning more about the complexities of issues affecting the Middle East and US rela- tions with the region. To learn more about the Middle East Institute, visit our website at http://www.mideasti.org The maps on pages 96-103 are copyright The Foundation for Middle East Peace. Our thanks to the Foundation for graciously allowing the inclusion of the maps in this publication. Cover photo in the top row, middle is © Tom Spender/IRIN, as is the photo in the bottom row, extreme left. -

Return of Organization Exempt from Income
Return of Organization Exempt From Income Tax Form 990 Under section 501 (c), 527, or 4947( a)(1) of the Internal Revenue Code (except black lung benefit trust or private foundation) 2005 Department of the Treasury Internal Revenue Service ► The o rganization may have to use a copy of this return to satisfy state re porting requirements. A For the 2005 calendar year , or tax year be and B Check If C Name of organization D Employer Identification number applicable Please use IRS change ta Qachange RICA IS RAEL CULTURAL FOUNDATION 13-1664048 E; a11gne ^ci See Number and street (or P 0. box if mail is not delivered to street address) Room/suite E Telephone number 0jretum specific 1 EAST 42ND STREET 1400 212-557-1600 Instruo retum uons City or town , state or country, and ZIP + 4 F nocounwro memos 0 Cash [X ,camel ded On° EW YORK , NY 10017 (sped ► [l^PP°ca"on pending • Section 501 (Il)c 3 organizations and 4947(a)(1) nonexempt charitable trusts H and I are not applicable to section 527 organizations. must attach a completed Schedule A ( Form 990 or 990-EZ). H(a) Is this a group return for affiliates ? Yes OX No G Website : : / /AICF . WEBNET . ORG/ H(b) If 'Yes ,* enter number of affiliates' N/A J Organization type (deckonIyone) ► [ 501(c) ( 3 ) I (insert no ) ] 4947(a)(1) or L] 527 H(c) Are all affiliates included ? N/A Yes E__1 No Is(ITthis , attach a list) K Check here Q the organization' s gross receipts are normally not The 110- if more than $25 ,000 . -

APF Newsletter, Winter 2006 – 2007
Winter 2006-2007 APF A Newsletter of the From The President AmericanEmergency Physicians andFellowship Disaster Preparednessfor Medicine in Israel Course News in Israel From The President Israel in Crisis Mission August 2006 would like to share with our members and donors the important by Dr. Dan Moskowitz I APF activities of the past 6 months. his past August, I had the privilege of being invited to par- 1. APF ISRAEL CRISIS FUND REPORT After placing on our T ticipate in an Emergency APF Mission to Israel with APF website and sending a special crisis appeal from Dr. Danny Laor, Board members Drs. Mike Frogel, Paul Liebman and Charles the Deputy Minister for Emergency Preparedness, on the critical Kurtzer. Dr. Boaz Tadmor organized an incredible, whirlwind needs of the Northern hospitals, it was very gratifying indeed that over $100,000 tour for us, only two days after the cessation of hostilities in was received for our Crisis Fund. All of this will be distributed to hospitals such as Israel. We were provided with a unique glimpse of the Israeli Sieff Hospital in Safed, Poriya in Tiberias, Western Galilee Medical Center in Nahariya, and Rambam Medical Center in Haifa, with the hospital CEO’s given the healthcare system under stress, including face-to-face meet- discretion as to how best to utilize these funds to help their hospital in light of the ings with top healthcare officials, as well as visits to the trau- recent crisis. matized hospitals in northern Israel. Perhaps most importantly, we visited 2. MISSION TO ISRAEL Three APF Board members, Drs. -

United Nations Conciliation.Ccmmg3sionfor Paiestine
UNITED NATIONS CONCILIATION.CCMMG3SIONFOR PAIESTINE RESTRICTEb Com,Tech&'Add; 1 ORIGINAL: ENGLISH APPENDIX J$ NON - JlXWISHPOPULATION WITHIN THE BOUNDARXESHELD BY THE ISRAEL DBFENCEARMY ON X5.49 AS ON 1;4-,45 IN ACCORDANCEWITH THE PALESTINE GOVERNMENT VILLAGE STATISTICS, APRIL 1945. CONTENTS Pages SUMMARY..,,... 1 ACRE SUB DISTRICT . , , . 2 - 3 SAPAD II . c ., * ., e .* 4-6 TIBERIAS II . ..at** 7 NAZARETH II b b ..*.*,... 8 II - 10 BEISAN l . ,....*. I 9 II HATFA (I l l ..* a.* 6 a 11 - 12 II JENIX l ..,..b *.,. J.3 TULKAREM tt . ..C..4.. 14 11 JAFFA I ,..L ,r.r l b 14 II - RAMLE ,., ..* I.... 16 1.8 It JERUSALEM .* . ...* l ,. 19 - 20 HEBRON II . ..r.rr..b 21 I1 22 - 23 GAZA .* l ..,.* l P * If BEERSHEXU ,,,..I..*** 24 SUMMARY OF NON - JEWISH'POPULATION Within the boundaries held 6~~the Israel Defence Army on 1.5.49 . AS ON 1.4.45 Jrr accordance with-. the Palestine Gp~ernment Village ‘. Statistics, April 1945, . SUB DISmICT MOSLEMS CHRISTIANS OTHERS TOTAL ACRE 47,290 11,150 6,940 65,380 SAFAD 44,510 1,630 780 46,920 TJBERIAS 22,450 2,360 1,290 26,100 NAZARETH 27,460 Xl, 040 3 38,500 BEISAN lT,92o 650 20 16,590 HAXFA 85,590 30,200 4,330 120,520 JENIN 8,390 60 8,450 TULJSAREM 229310, 10 22,320' JAFFA 93,070 16,300 330 1o9p7oo RAMIIEi 76,920 5,290 10 82,220 JERUSALEM 34,740 13,000 I 47,740 HEBRON 19,810 10 19,820 GAZA 69,230 160 * 69,390 BEERSHEBA 53,340 200 10 53,m TOT$L 621,030 92,060 13,710 7z6,8oo . -

Run Water Management
Economic Analysis of Long- Run Water Management by Eli Feinerman (Hebrew University) Israel Finkelshtain (Hebrew University) Franklin Fisher (MIT) Annette Huber-Lee (SEI) Brian Joyce (SEI) Iddo Kan (Hebrew University) Ami Reznik (Hebrew University) Funded by the Parsons Water Fund Water Management in Israel Property rights: By law, all water sources are state property, centrally managed by the Water Authority. Managing water supply: . Extraction licenses and fees based on metering; . Contracts with desalination plants and wastewater- treatment plants. Preparing a long-run program of infrastructural development. Managing water consumption: Prices and quotas (increasing block-rate tariffs) of freshwater, treated wastewater and brackish water, for urban, industrial, agricultural and environmental uses. Management considerations: Supply reliability, cost recovery, equity, efficiency, externalities. The Multi- Year Water Allocation System model Topology Model Topology Sea Water and Urban Waste Water National Brackish and Water Sources Agricultural Ground Water Natural Fresh Demand Treatment Carrier Surface Water Demand Nodes Desalination Water Sources Nodes Plants Junctions Sources Plants 3100 3000 1100 1000 Golan 1200 5000 Golan Sea of Galilee Golan Carmel • 16 aquifers Golan Zalmon Coast Local 3001 Eastern 3101 Galilee 1201 1001 Tzfat Tzfat Golan 3002 Western • 19 wastewater treatment plants Galilee 1202 3102 Kineret 1002 Kineret Western Kineret 3003 GW Lower Jordan 1101 River Hadera 3103 1203 5001 Menashe WG Acco Beit Shean • 3 surface -

List of Cities of Israel
Population Area SNo Common name District Mayor (2009) (km2) 1 Acre North 46,300 13.533 Shimon Lancry 2 Afula North 40,500 26.909 Avi Elkabetz 3 Arad South 23,400 93.140 Tali Ploskov Judea & Samaria 4 Ariel 17,600 14.677 Eliyahu Shaviro (West Bank) 5 Ashdod South 206,400 47.242 Yehiel Lasri 6 Ashkelon South 111,900 47.788 Benny Vaknin 7 Baqa-Jatt Haifa 34,300 16.392 Yitzhak Veled 8 Bat Yam Tel Aviv 130,000 8.167 Shlomo Lahiani 9 Beersheba South 197,300 52.903 Rubik Danilovich 10 Beit She'an North 16,900 7.330 Jacky Levi 11 Beit Shemesh Jerusalem 77,100 34.259 Moshe Abutbul Judea & Samaria 12 Beitar Illit 35,000 6.801 Meir Rubenstein (West Bank) 13 Bnei Brak Tel Aviv 154,400 7.088 Ya'akov Asher 14 Dimona South 32,400 29.877 Meir Cohen 15 Eilat South 47,400 84.789 Meir Yitzhak Halevi 16 El'ad Center 36,300 2.756 Yitzhak Idan 17 Giv'atayim Tel Aviv 53,000 3.246 Ran Kunik 18 Giv'at Shmuel Center 21,800 2.579 Yossi Brodny 19 Hadera Haifa 80,200 49.359 Haim Avitan 20 Haifa Haifa 265,600 63.666 Yona Yahav 21 Herzliya Tel Aviv 87,000 21.585 Yehonatan Yassur 22 Hod HaSharon Center 47,200 21.585 Hai Adiv 23 Holon Tel Aviv 184,700 18.927 Moti Sasson 24 Jerusalem Jerusalem 815,600 125.156 Nir Barkat 25 Karmiel North 44,100 19.188 Adi Eldar 26 Kafr Qasim Center 18,800 8.745 Sami Issa 27 Kfar Saba Center 83,600 14.169 Yehuda Ben-Hemo 28 Kiryat Ata Haifa 50,700 16.706 Ya'akov Peretz 29 Kiryat Bialik Haifa 37,300 8.178 Eli Dokursky 30 Kiryat Gat South 47,400 16.302 Aviram Dahari 31 Kiryat Malakhi South 20,600 4.632 Motti Malka 32 Kiryat Motzkin Haifa -
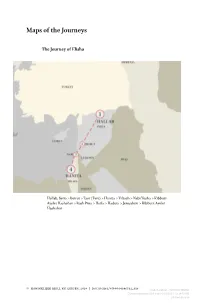
Downloaded from Brill.Com10/03/2021 12:34:51AM Via Free Access Maps of the Journeys 323
Maps of the Journeys The Journey of Elisha Hallab, Syria > Beirut > Tsor (Tyre) > Hanita > Yiftach > Nebi Yusha > Kibbutz Ayelet Hashahar > Rosh Pina > Haifa > Hadera > Jerusalem > Kibbutz Ayelet Hashahar © koninklijke brill nv, leiden, 2019 | doi:10.1163/9789004396562_018 Gadi BenEzer - 9789004396562 Downloaded from Brill.com10/03/2021 12:34:51AM via free access Maps of the Journeys 323 The Journey of Yirmi Varlista, Poland > Lutza > Drohobych > Stryy > Buluchov > Siberia > Toms > Asimo > Bukhara > Kazakhstan, Karleshods > Pahlavi > Albroz Mountains > Teheran > Abadan > Karachi > Aden > Seuz > Kantara > Sinai > Hadera > Atlit > Jerusalem > Degania Gadi BenEzer - 9789004396562 Downloaded from Brill.com10/03/2021 12:34:51AM via free access 324 Maps of the Journeys The Journey of Bracha San’ah > Yemen > Aden > Egypt, Sinai > Port Sa’yid > Atlit > Tel Aviv Gadi BenEzer - 9789004396562 Downloaded from Brill.com10/03/2021 12:34:51AM via free access Maps of the Journeys 325 The Journey of Yair Czernowitz > Rumania > Radowitz > Bucharest > Tamishawar > Zagreb, Yugoslavia > Port of Split, Yugoslavia > Port of Haifa > Cyprus > Atlit > Kiryat Shmuel > Kiryat Binyamin > Magdiel Gadi BenEzer - 9789004396562 Downloaded from Brill.com10/03/2021 12:34:51AM via free access 326 Maps of the Journeys The Journey of Oscar Baghdad > Shatt Al Arab > Persia, Teheran > Shhar Ha’Aliyah, Haifa > Jerusalem > Menahamia > Tel Aviv > Kibbutz Sasa > Nahariya > Rambam Hospital in Haifa > Hadassa in Jerusalem > Tel Aviv > Kiryat Arie Gadi BenEzer - 9789004396562 Downloaded -

APF H N P D N a F R C I I E R
Winter 2011-2012 sicians y a APF h n P d n a F r c i i e r n e A Newsletter of the d m s News American Physicians and Friends A for Medicine in Israel APF - Supporters of Medicine in Israel 2001 Beacon Street, Suite 210, Boston, MA 02135 617-232-5382 [email protected] From the President 2. The Fellowship Awards Program Since 1950 APF has awarded over 1500 fellowship awards totaling over $4 million. As I’ve indicated in past columns, if one looks at the past and current roster of leaders of Israeli medicine, the vast majority of them have been APF fellows in the past. 3. The Student Programs Under the very able leadership of Drs. Alan Menkin and Charles Kurtzer each year up to 40 North American medical It has been a pleasure and an honor to students have gone to Israel for 10 days serve as APF President from 2006 to under the joint sponsorship of Taglit/ 2011. As my term of office draws to a birthright. This has included two days of close I would like to highlight some of the activities with the Israel Defense Force important events of the past five years. Medical Corps, The Israeli Ministry of Health, and the Computer Simulation 1. Emergency Medical Volunteer (EMV) Center at Tel HaShomer Hospital. Courses and Registry In the last five years the EMV Registry 4. Corporate Membership has become fully operational. Working in Under the visionary leadership of Dr. close association with the Israeli Defense Paul Scherer, APF now has Corporate Forces Medical Corps and The Ministry Members and we are grateful for their of Health we now have records of over continued support. -

Price Tag and Extremist Attacks in Israel
Price Tag and Extremist Attacks in Israel Since 2008, there have been repeated attacks carried out by extremist Israeli Jews against Israeli Arabs and Palestinians, often in reprisal for Israeli government action against illegal settlement activity. These attacks, which are frequently labeled “price tag” incidents, target mosques, churches, Arab and Jewish homes and property, Israeli military bases and vehicles, as well as other Israeli Jews. They involve the desecration of property with anti-Arab and anti-government slogans. Most of these attacks include the phrase “price tag” and are accompanied by hateful and racist slogans, the name of an illegal settlement, or a reference to an Israeli casualty of Palestinian terrorism, the implication being that the violent incident is the “cost” of Israeli government action on settlements or for anti-Israeli violence. There have also been a number of violent and deadly arson attacks carried out by extremists who, according to Israeli law enforcement, seek to destabilize the country and overthrow the Israeli government in order to establish a new regime to be based on Jewish law. The Israeli police have established a special unit tasked with cracking down on those committing price tag assaults. Many top Israeli leaders have condemned the price tag phenomenon and other extremist attacks, including Prime Minister Netanyahu, former President Peres and President Rivlin and other senior elected officials, religious leaders and members of civil society. ADL has also taken a strong public position on the issue, and has repeatedly issued unqualified condemnations of price tag attacks, called on law enforcement 1 / 9 officials to investigate suspected incidents and prosecute those responsible, and encouraged prominent Israel political, religious and societal leaders to speak out against the underlying hatred and racism that motivates price tag attacks. -

Leviathan Project: Supplemental Lender Information Package – Overarching Environmental and Social Assessment Document
Prepared for: Leviathan Project: Supplemental Noble Energy Lender Information Package – Overarching Environmental and Social Assessment Document September 2016 Environmental Resources Management 1776 I St NW Suite 200 Washington, DC 20006 www.erm.com The business of sustainability FINAL Prepared for: Noble Energy Leviathan Project: Supplemental Lender Information Package – Overarching Environmental and Social Assessment Document September 2016 Peter Rawlings Partner Environmental Resources Management 1776 I St NW Suite 200 Washington, DC 20006 202.466.9090(p) 202.466.9191(f) DISCLAIMER: This document has been created and is submitted as part of the application made by NOBLE ENERGY INTERNATIONAL LTD for OPIC's political risk insurance for the Leviathan project; The sole purpose of this document is to demonstrate alignment with applicable lender standards; This document is not intended to create nor does it create any legally binding obligation and/or commitment by NOBLE ENERGY INTERNATIONAL LTD or any of its subsidiaries or affiliates towards any third parties under applicable laws, including, without limitation, US and Israeli laws. ERM LEVIATHAN PROJECT-NOBLE ENERGY-SEPTEMBER 2016 TABLE OF CONTENTS 1.0 SUMMARY 1 2.0 INTRODUCTION 0 2.1 BACKGROUND 0 2.2 PURPOSE OF DOCUMENT 1 2.3 RELEVANT DOCUMENTS AND INFORMATION 1 2.4 STRUCTURE OF THIS DOCUMENT 2 3.0 PROJECT DESCRIPTION AND OVERVIEW 4 3.1 PROJECT DESCRIPTION 4 3.1.1 Offshore Components 4 3.1.2 Onshore Components 5 3.2 ASSOCIATED FACILITIES 8 3.2.1 Gas Transportation in Existing INGL Network -

Politically Or Personally Motivated Appointments and Engagements in Local Authorities After the 2013 Elections
Local Authorities Report 2016 Politically or Personally Motivated Appointments and Engagements in Local Authorities after the 2013 Elections Summary General Background On October 22, 2013, elections were held in 187 local authorities for head of the local authority and its council. A second round of elections was held on November 5, 2013 in 38 local authorities where no candidate for mayor received 40% of the legitimate votes1 in the first round. Following the two election rounds, the mayor was replaced in some 90 local authorities. In most local authorities where a new mayor was voted in, many new workers were hired to staff either existing or new positions. Civil service in Israel is based on a conception formulated in the early days of the State of Israel: a service of a national, professional nature devoid of any political interest, which implements the policy of the elected civil servants. The officials in the service are not replaced following a change in the local government. Regarding the negative phenomenon of political appointments, the Israel Supreme Court had this to say2: "A public authority which appoints a worker in the civil service, acts as a trustee of the public interest, the overarching rule being that such a trusteeship must be exercised with fairness and integrity, devoid of all extraneous considerations and in the interest of the public by virtue of which and for the benefit of which the power of appointment is given to the appointing authority… When a civil servant appoints a worker in the civil service based on extraneous considerations of political/partisan interests, such an appointment is not legitimate, as it is a breach of trust of the public which empowered the appointing authority." The employee hiring procedure in a municipality was established by the Minister of Finance in the Municipalities Regulations [Tenders for Hiring Employees], 5740-1979 (hereinafter: "hiring regulations"). -

HAIFA 527 Natanson — Neuer
HAIFA 527 Natanson — Neuer Natanson Dr lit it.1 Internal Diseases Navon Josel & Miriam Neiger Abraham & Rachel NESHER IContd) 61 Moriya 8 29 44 55c Derech Tzorfat 52 62 03 4 Sederot Sinai 8 85 04 D Givon Res 8 16 77 Natanzon Shelomo Navon Pinchas 83 Hanita 6 72 68 Neiger Dr David 1 5 David Pinsky. 8 32 15 L Klavansky Res 8 53 47 18 Sederot Rothschild 52 75 19 Navon Sima 19 Aliya 52 16 49 Neiger Itzhak & Tamar Dr L Loewenstein Res 8 53 49 Nath Hans Meir Advct Navot Jechiel 5 Ilanot 8 31 77 2a Netiv Hen 6 29 86 M Muller Res 8 18 05 6 Habrecha 6 87 80 Navot Shimon 6a Eder 8 36 45 Neiger Nehama D Oreg Res 7 24 36 Navot Dr Yisrael 14 Sederot Mapu8 64 98 Shikun Gilboa 17/4 6 08 17 D Rapaport Res 52 30 41 Nathan Dr II Advct & Notary Neikrug Moshe 27 Pevsner 6 22 25 B Shapiro Res 8 17 79 33 Herzl 6 47 03 Navoth Pesach Chem Eng E Solowieiczyk Res 6 63 46 Res 41 Hayarkon 8 16 79 56 Shoshanat Hacarmel 8 35 53 Neilinger Geula Nesher Meir 27 Ilanot 8 60 60 Nathan Gertrud 55 Derech Hayani8 66 77 Navratzki Dr Curt Economic Adviser 3 Atzmaut Kiryat Yam B' 7 50 57 Neiman Izaak Nesher Yisrael Nathan H & Y 5 Melchett 6 29 17 710b Denya Hod Hacarmel 8 79 35 20a Sederot Trumpeldor 6 99 07 Navy Yaacov 47 Moriya 8 29 63 8 Leonardo Da Vinci 8 91 58 Nathan Isaac Advct 60 Abbas...52 49 98 Naymarke Nahum Driver 26 Sederot NeisserRosa 6 Ayalon 8 48 65 Neshling Dov Wei/man Kiryat Motzkin 7 42 28 Neistat Dr Lacaro 6a Hantke 8 91 56 46 Yod-Het Kiryat Hayim 7 52 69 Nathan Istried NEAR EAST BONDED LTD Neiwirth Sonia 17a Rabbi Akiva .