DOCSLIB.ORG

Ionic Interactions in Lanthanide Halides

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Ionic Interactions in Lanthanide Halides Ionic Interactions in Lanthanide Halides Z. Akdeniz, Z. Çiçek, and M. P. Tosia Department of Physics, University of Istanbul, Istanbul, Turkey and Abdus Salam International Centre for Theoretical Physics, 1-34014 Trieste, Italy a INFM and Classe di Scienze, Scuola Normale Superiore, 1-56126 Pisa, Italy Reprint requests to Prof. M. P. T.; Fax: +39-050-563513; E-mail: [email protected] Z. Naturforsch. 55 a, 861-866 (2000); received September 27, 2000 We determine a model of the ionic interactions in RX3 compounds (where R is a metal in the rare-earth series from La to Lu and X = CI, Br or I) by an analysis of data on the static and dynamic structure of their molecular monomers. The potential energy function that we adopt is patterned after earlier work on Aluminium trichloride [Z. Akdeniz and M. P. Tosi, Z. Naturforsch. 54a, 180 (1999)], but includes as an essential element the electric polarizability of the trivalent metal ion to account for a pyramidal shape of RX3 molecules. From data referring mostly to trihalides of elements at the ends and in the middle of the rare-earth series (/. e. LaX3, GdX3 and LuX3), we propose systematic variations for the effective valence, ionic radius and electric polarizability of the metal ions across the series. As a first application of our results we predict the structure of the Dy2Cl6 and Dy2Br6 molecular dimers and demonstrate by comparison with electron diffraction data that lanthanide-ion polarizability plays a quantitative role also in this state of tetrahedral-like coordination. Key words: Ionic Clusters; Molten Salts. 1. Introduction a number of years a matter of controversy. Although the majority of the data supports slightly pyramidal Industrial and technical applications have moti- shapes for RX3 gaseous molecules, the question as to vated interest in rare-earth halides for a number of which of these are planar (D3h symmetry) and which years. Great attention has been given to their vapours are pyramidal (C3v symmetry) does not seem to be and to the volatile vapour complexes that are formed fully settled experimentally [1]. The assignment of with complexing agents such as the alkali halides vibrational frequencies on the basis of C3v symmetry or the Al trihalides, in view of a series of poten- [1] yields relatively low values for the frequency of tial applications related to new energy sources, en- the u2 mode, indicating that these molecules are quite ergy conservation, and recycling or separation pro- floppy. cesses [ 1 ]. The extraction and processing of rare-earth On the theoretical side, extended Hiickel calcula- metals are based on molten-salt technologies, giv- tions by Myers et al. [5] predicted a pyramidal config- ing incentive to current efforts at determining ther- uration for all these molecules, with the X-R-X bond modynamic and structural properties of rare-earth angle increasing both across the lanthanide series and halide melts by both experimental and simulational across the halogen series from 91° in LaF3 to 119° methods [2], in Lul3. Attention has also been drawn to the role In attempting to develop a refined model for the of ionic polarizabilities in determining the molecular ionic interactions in rare-earth halides it seems natural shape [6]. Within a simple ionic model the distortion to follow the approach developed by two of us [3] for of an RX3 molecule from a planar to a pyramidal Al chlorides and alkali chloroaluminates: that is, to shape is driven by the energy gain from electric po- start by examining the static and dynamic structure larization of the rare-earth ion: a pyramidal shape is of the simplest molecular units, which are the RX3 then favoured by a high polarizability of the rare-earth monomers. As evidenced in the work of Molnär and ion and by a short X-R bond length. This prediction Hargittai [4], the shape of these molecules has been for is in accord with the trends revealed by the molecu- 0932-0784 / 2000 / 0900-1100 $ 06.00 © Verlag der Zeitschrift für Naturforschung, Tübingen • www.znaturforsch.com 862 Z. Akdeniz et al. • Ionic Interactions in Lanthanide Halides lar orbital calculations of Myers et al. [5]. However, 2. Interionic Force Model and Evaluation of for quantitative purposes the available value of the Model Parameters lanthanide-ion polarizability obtained by Pauling [7] is likely to be much too low. The rare-earth ions do not Following our earlier study of the Al-based chlo- seem to have been considered in the re-assessments rides [3], the microscopic model that we use for lan- of the Pauling polarizability scale due to Tessman, thanide halide clusters incorporates the Born model Kahn and Shockley [8] and to later workers [9]. The of cohesion [10] and the shell model for vibrational work of these authors led to a very sizable increase of motions and crystal defects [11]. Electron-shell de- the polarizability over the Pauling values for all other formability is described through (i) effective valences positive ions, and in particular to an increase by about Zi subject to overall charge compensation; (ii) the a factor of two for the doubly charged alkaline-earth electric and overlap polarizabilities of the halogens ions. (denoted by a\ and as, respectively); and (iii) the electric polarizability OR of the lanthanide ions. Over- Therefore, our first task in the present work is to lap repulsions of exponential form involve ionic radii obtain a new estimate for the electric polarizability of Ri and stiffness parameters p . Van der Waals dipole- the lanthanide ions. We focus for this purpose on those x dipole interactions are included for the halogens. gaseous RX3 molecules for which electron diffraction data are available to provide evidence for a pyramidal For convenience we report here the form of the shape and a value for the X-R-X bond angle. These potential energy [/({r^}, {Pj}) as a function of the mainly are the chloride, bromide and iodide of La, bond vectors r^ and of the electric dipole moments pz carried by the ions. This is Gd and Lu (excepting Lal3), and their study presents two evident advantages: (i) these elements are at the beginning, in the middle and at the end of the rare- f({r«}, b,}) = E +*«ovi) - earth series, so that their inclusion in the analysis i<j Tij facilitates an assessment of trends ; and (ii) the elec- c tron distribution in the f-shell of these elements in the + t/p ;i({rlj},{pj)+t/shell({rl,},{pj).(l) isolated state is spherically symmetrical, thus exclud- ing that f-shell anisotropy may be relevant in driving The overlap repulsive energy in (1) is taken in the a pyramidal distortion as discussed by Molnär and Busing form [12] Hargittai [4]. In view of the presumable uncertainties in the mea- #ij(r) = f(Pi + Pj) exp[(i?i + Rj - r)/(pi + Pj)l (2) sured pyramidal bond angles, our main aim is the as- The reader is referred to our earlier work [3] for ex- sessment of trends in the ionic-model parameters for pressions of the classical polarization energy and the trivalent ions across the rare-earth series, rather of the shell deformation energy Usht\\. than their individual values in each system. These A very helpful aspect of the model (1) is that trans- parameters are the electric polarizability, the effec- ferability of the parameters describing the halogen tive valence and the ionic radius entering the core ions and direct proportionality between the charac- repulsion. In Sect. 2, after a brief reminder of the teristic radius RR and the hardness parameter pR of essence of our model as developed in [3], we list the the metal ion are approximately valid. We expect input values of the other model parameters and the (and, as we shall see below, find) that the rare-earth available evidence on bond lengths, bond angles and compounds of present interest are rather highly ionic vibrational mode frequencies in each of the gaseous molecules that we have taken into consideration. The Table 1. Input of interionic force parameters for rare-earth trends of the model parameters for the lanthanide ions trihalidesa. across the series of rare-earth trihalides are presented X 2 2 R 3 3 5 2 and discussed in Sect. 3. A first test of our results / (e /Ä ) r'PR ax(A ) as (A ) Cx (eÄ / ) is reported in Sect. 4, by giving a prediction of the CI 0.05 18.6 3.00 0.83 5.50 structure of the Dy chloride and bromide dimers and Br 0.05 18.6 4.17 1.2 7.17 comparing it with evidence from electron diffraction I 0.05 18.6 6.29 1.7 10.1 experiments. Finally, Sect. 5 ends the paper with a a The polarizability ax is taken from [9], the other parameters brief summary and outlook. from [13]. Z. Akdeniz et al. • Ionic Interactions in Lanthanide Halides 863 Table 2. Bond lengths rRX (Ä), bonds angles ZX-R-X (de- Table 2 also includes the values that we have ob- -1 grees) and vibrational frequencies (cm ) of selected RX3 tained for the other vibrational frequencies of these d molecules . molecules. It should be noted that many of the mode Molecule R ZX-R-X U frequencies reported in the literature are mere esti- RX "1 2 "3 mates and that there is a very appreciable spread in 14,22 LaCl3' ' 2.56 116.5 336.8 52.1 332.5 72.6 the frequencies from different experiments and differ- 333 26 63 1 LaBr,' -^] 2.74 115.5 190 35 220 47 ent sources, as discussed for instance by Koväcs et al.
Load more

Recommended publications
  • Additional Teacher Background Chapter 4 Lesson 3, P. 295
    Additional Teacher Background Chapter 4 Lesson 3, p. 295 What determines the shape of the standard periodic table? One common question about the periodic table is why it has its distinctive shape. There are actu- ally many different ways to represent the periodic table including circular, spiral, and 3-D. But in most cases, it is shown as a basically horizontal chart with the elements making up a certain num- ber of rows and columns. In this view, the table is not a symmetrical rectangular chart but seems to have steps or pieces missing. The key to understanding the shape of the periodic table is to recognize that the characteristics of the atoms themselves and their relationships to one another determine the shape and patterns of the table. ©2011 American Chemical Society Middle School Chemistry Unit 303 A helpful starting point for explaining the shape of the periodic table is to look closely at the structure of the atoms themselves. You can see some important characteristics of atoms by look- ing at the chart of energy level diagrams. Remember that an energy level is a region around an atom’s nucleus that can hold a certain number of electrons. The chart shows the number of energy levels for each element as concentric shaded rings. It also shows the number of protons (atomic number) for each element under the element’s name. The electrons, which equal the number of protons, are shown as dots within the energy levels. The relationship between atomic number, energy levels, and the way electrons fill these levels determines the shape of the standard periodic table.
    [Show full text]
  • ELECTRONEGATIVITY D Qkq F=
    ELECTRONEGATIVITY The electronegativity of an atom is the attracting power that the nucleus has for it’s own outer electrons and those of it’s neighbours i.e. how badly it wants electrons. An atom’s electronegativity is determined by Coulomb’s Law, which states, “ the size of the force is proportional to the size of the charges and inversely proportional to the square of the distance between them”. In symbols it is represented as: kq q F = 1 2 d 2 where: F = force (N) k = constant (dependent on the medium through which the force is acting) e.g. air q1 = charge on an electron (C) q2 = core charge (C) = no. of protons an outer electron sees = no. of protons – no. of inner shell electrons = main Group Number d = distance of electron from the nucleus (m) Examples of how to calculate the core charge: Sodium – Atomic number 11 Electron configuration 2.8.1 Core charge = 11 (no. of p+s) – 10 (no. of inner e-s) +1 (Group i) Chlorine – Atomic number 17 Electron configuration 2.8.7 Core charge = 17 (no. of p+s) – 10 (no. of inner e-s) +7 (Group vii) J:\Sciclunm\Resources\Year 11 Chemistry\Semester1\Notes\Atoms & The Periodic Table\Electronegativity.doc Neon holds onto its own electrons with a core charge of +8, but it can’t hold any more electrons in that shell. If it was to form bonds, the electron must go into the next shell where the core charge is zero. Group viii elements do not form any compounds under normal conditions and are therefore given no electronegativity values.
    [Show full text]
  • Periodic Table of the Elements Notes
    Periodic Table of the Elements Notes Arrangement of the known elements based on atomic number and chemical and physical properties. Divided into three basic categories: Metals (left side of the table) Nonmetals (right side of the table) Metalloids (touching the zig zag line) Basic Organization by: Atomic structure Atomic number Chemical and Physical Properties Uses of the Periodic Table Useful in predicting: chemical behavior of the elements trends properties of the elements Atomic Structure Review: Atoms are made of protons, electrons, and neutrons. Elements are atoms of only one type. Elements are identified by the atomic number (# of protons in nucleus). Energy Levels Review: Electrons are arranged in a region around the nucleus called an electron cloud. Energy levels are located within the cloud. At least 1 energy level and as many as 7 energy levels exist in atoms Energy Levels & Valence Electrons Energy levels hold a specific amount of electrons: 1st level = up to 2 2nd level = up to 8 3rd level = up to 8 (first 18 elements only) The electrons in the outermost level are called valence electrons. Determine reactivity - how elements will react with others to form compounds Outermost level does not usually fill completely with electrons Using the Table to Identify Valence Electrons Elements are grouped into vertical columns because they have similar properties. These are called groups or families. Groups are numbered 1-18. Group numbers can help you determine the number of valence electrons: Group 1 has 1 valence electron. Group 2 has 2 valence electrons. Groups 3–12 are transition metals and have 1 or 2 valence electrons.
    [Show full text]
  • Periodic Table 1 Periodic Table
    Periodic table 1 Periodic table This article is about the table used in chemistry. For other uses, see Periodic table (disambiguation). The periodic table is a tabular arrangement of the chemical elements, organized on the basis of their atomic numbers (numbers of protons in the nucleus), electron configurations , and recurring chemical properties. Elements are presented in order of increasing atomic number, which is typically listed with the chemical symbol in each box. The standard form of the table consists of a grid of elements laid out in 18 columns and 7 Standard 18-column form of the periodic table. For the color legend, see section Layout, rows, with a double row of elements under the larger table. below that. The table can also be deconstructed into four rectangular blocks: the s-block to the left, the p-block to the right, the d-block in the middle, and the f-block below that. The rows of the table are called periods; the columns are called groups, with some of these having names such as halogens or noble gases. Since, by definition, a periodic table incorporates recurring trends, any such table can be used to derive relationships between the properties of the elements and predict the properties of new, yet to be discovered or synthesized, elements. As a result, a periodic table—whether in the standard form or some other variant—provides a useful framework for analyzing chemical behavior, and such tables are widely used in chemistry and other sciences. Although precursors exist, Dmitri Mendeleev is generally credited with the publication, in 1869, of the first widely recognized periodic table.
    [Show full text]
  • • What I Hope to Convey to You Is That Rare Earths Are Uniquely Required for High Performance Magnets
    • What I hope to convey to you is that rare earths are uniquely required for high performance magnets. • First a quick introduction to Arnold – the company I’ve worked for since 1992. • Arnold’s history in magnetics and magnetic materials extends back to 1895 and has included almost every commercially supplied permanent and soft magnetic product. • Today Arnold is focused on: SmCo, Alnico and bonded permanent magnets; precision thin metals – both magnetic and non-magnetic; magnetic assemblies for motors, magnetic levitation, sensing and separation technologies; and most recently we have responded to customer requests to develop and supply ultra-high performance permanent magnet motors for select applications. • Let’s start by answering this question: What makes rare earth elements so special? • The rare earth elements consist of the 15 lanthanide elements (lanthanum to lutetium) plus yttrium and scandium. • Yttrium and scandium are directly above lanthanum in the periodic table and have chemical properties that are very similar to the lanthanides – that is why they are usually included with them. • Note cesium and barium precede lanthanum in row 6 of the periodic table and that hafnium, element number 72, continues row 6 right after lutetium, the lanthanide with the highest atomic number, 71. • Note too, row 4 of the table which contains the transition elements including iron, cobalt and nickel. We’ll be making some comparison between the two groups of elements in later slides. • Rare earth elements (REEs) have considerable chemical similarities thus making them difficult to separate from each other. • That is one reason they were late in being discovered, isolated and incorporated in alloys and compounds.
    [Show full text]
  • 24. SOLUTION CHEMISTRY of the LANTHANIDE ELEMENTS Gregory
    .24. SOLUTION CHEMISTRY OF THE LANTHANIDE ELEMENTS Gregory R. Choppin Department of Chemistry Florida State University Tallahassee, Florida 32306,U.S.A. ABSTRACT Complexes of the lanthanide elements provide insight into the factors which are important in ionically bonded systems. The enthalpy and entropy terms of complexation are a measure of the role of hydration effects while the free energy measures the metal-ligand interaction. The role of ligand basicity in the nature of the complex as an inner sphere or a solvent- separated outer sphere species is reviewed. An equation which has been used successfully to calculate stability constants which agree with experimental values is described and shown to be useful in establishing models for lanthanide complexing. The stability of complexes as a function of canonical structure of organic ligands and of ligand ring size is discussed. A study of charge polarization in conjugated organic ligands complexed by lanthanide cations is described. .25. SOLUTION CHEMISTRY OF THE LANTHANIDE ELEMENTS I. INTRODUCTION The development of separation methods using ion exchange resins has provided chemists with large quantities of very pure individual lanthanide elements. As a result, in the last 30 years research in lanthanide chemistry has been relatively intensive and has led to a rather satisfactory understanding of the chemical behavior of these elements as well as to the growing utilization of them in a variety of technological applications. A central feature of lanthanide chemistry is the strongly ionic character of the bonding between lanthanide cations and other atoms. As a result of this ionicity, they can be classified as "hard" (strongly acidic) cations.
    [Show full text]
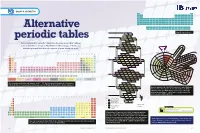
  • Alternative Periodic Tables Have Been Proposed That Address Mn Fe 25 28 Cr P S Co Some of the Shortcomings of Mendeleev’S Table (See Pp
    GROUP 4: CHEMISTRY H He Li Be B C N O F Ne Na Mg Al Si P S Cl Ar K Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Kr Rb Sr Y Zr Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb Te I Xe Cs Ba La Hf Ta W Re Os Ir Pt Au Hg Tl Pb Bi Po At Rn Fr Ra Ac Rf Db Sg Bh Hs Mt Ds Rg Cn Nh Fl Mc Lv Ts Og Ce Pr Nd Pm Sm Eu Gd Td Dy Ho Er Tm Yb Lu Alternative Th Pa U Np Pu Am Cm Bk Cf Es Fm Md No Lr n=1 Simplified periodic table H He* 1 2 N O n=2 7 8 C Li Be F• periodic tables 6 3 4 9 B Ne* 5 10 Several alternative periodic tables have been proposed that address Mn Fe 25 28 Cr P S Co some of the shortcomings of Mendeleev’s table (see pp. 2–6). Do you n=3 24 15 16 27 V Si Na Mg Cl• Ni PERIODICPERIODIC 23 14 11 12 17 28 DIVIDE think they work better than the version on your classroom wall? Ti Al Ar* Cu 22 2 2 29 ALKALI Sc Zn 21 30 METALS NOBLE 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Gd Tb GASES Uue 2 65 Og Ubn Cm 1 H He Eu Tc Ru Dy Fr SUPERACTINIDES Am Bk 63 43 44 66 Rn Pu Sm Mo As Se Rh Ho Np Gd Tb 2 Li Be B C N O F Ne Ra U Eu 62 42 33 34 45 67 Xe Cs n=4 Pa Sm Dy Cf Pm Nb Ge K Ca Br• Pb Er Th Pm 3 Na Mg Al Si P S Cl Ar 61 41 32 19 20 35 46 68 Ts Kr Rb Ba Ac Nd Ho Pr Er Es Nd Zr Ga Kr* Ag Tm At K Sr Tm 4 K Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Kr 60 40 31 36 47 69 I Ar Ce Fm La Yb Md Pr Y Cd Yb Br Na Ca Lu 59 39 48 70 Cl Ne No 5 Rb Sr Y Zr Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb Te I Xe He Li LANTHANIDES & ACTINIDESLr F Mg Y Ce Lu Be Hf Rf 58 71 O H Sc Zr 6 Cs Ba La Ce Pr Nd Pm Sm Eu Gd Td Dy Ho Er Tm Yb Lu Hf Ta W Re Os Ir Pt Au Hg Tl Pb Bi Po At Rn S Ta Db Se
    [Show full text]
  • I Anomalous Properties of Elements I That MOW "Long Periods" of Elements
    James E. Huheey and Caroline L. Huheey I Anomalous Properties of Elements University of Maryland College Park, 20742 I that MOW"Long Periods" of Elements The phenomenon known as the lantha- difficulties in their separation are well-documented (3). nide contraction has long been appreciated as an impor- Less well-explored are the cases in which the lanthanide tant factor in determining the properties of the lan- contraction results in different properties for the post- thanide and post-lanthanide elements. Appreciation lanthanide elements (4). In general, these may be re- of this phenomenon is of obvious heuristic value with lated to greater effective nuclear charge and attraction regard to research efforts directed towards these ele- for electrons in the heavier elements. ments. In addition there is an implicit pedagogical Table I lists the ground state ionization energies (6) value that has been discussed at some length (1) and for the elements rubidium-xenon (Period Five) and which is included in most descriptive discussions of these cesium-radon (Period Six). The pre-lanthanide ele- elements. It is the purpose of this paper to examine ments cesium, barium, and lanthanum have ionization the physical nature of this phenomenon and extend the energies less than their lighter congeners as expected for concept to other parts of the periodic table. the main group elements. The effect of the addition of fourteen protons to the nucleus and fourteen poorly shielding 4f electrons is a higher ionization energy for hafnium than for zirconium. 811 of the following sixth period transition elements have higher ionization ener- gies than their lighter congeners and the trend persists as far as lead.
    [Show full text]
  • Excited State Properties of Lanthanide Complexes: Beyond Ff States
    Inorganica Chimica Acta 359 (2006) 4130–4138 www.elsevier.com/locate/ica Excited state properties of lanthanide complexes: Beyond ff states Arnd Vogler *, Horst Kunkely Institut fu¨r Anorganische Chemie, Universita¨t Regensburg, D-93040 Regensburg, Germany Received 3 May 2006; accepted 27 May 2006 Available online 7 June 2006 Abstract Generally, metal-centered ff states dominate the discussion of the excited state properties of lanthanide complexes. In particular, the luminescence properties of Eu(III) and Tb(III) compounds have been studied in great detail for many decades. However, other types of excited states such as MC fd, MLCT, LMCT, MMCT and IL are also of interest. In this context, we have recently examined the excited state behavior of selected Ce(III), Ce(IV), Eu(II) and Gd(III) complexes which are luminescent and/or photoreactive. Ó 2006 Elsevier B.V. All rights reserved. Keywords: Electronic spectra; Luminescence; Photochemistry; Lanthanides; Cerium; Europium; Gadolinium 1. Introduction coefficients and the radiative lifetimes of ff states are rather large (10À3 s). Owing to the small absorption coefficients Lanthanide (Ln) compounds play an important role in of Ln3+, the excitation can be facilitated by suitable ligands the field of luminescence spectroscopy. In the ground which absorb the light and subsequently transfer the exci- states, the electron configuration of lanthanide cations tation energy to the emissive Ln3+ ion. In addition, appro- extends from f0 to f14. All lanthanides form stable com- priate ligands may prevent radiationless deactivations. This pounds in the oxidation state III, representing the ground behavior is illustrated by various Eu3+ and Tb3+ com- state configuration f1 (Ce3+)tof14 (Lu3+).
    [Show full text]
  • (A) Lanthanide (Ln) Zinc Telluride by Means of Experimental and Quantum-Chemical Techniques
    crystals Article Revealing the Bonding Nature in an ALnZnTe3-Type Alkaline-Metal (A) Lanthanide (Ln) Zinc Telluride by Means of Experimental and Quantum-Chemical Techniques Katharina Eickmeier and Simon Steinberg * Institute of Inorganic Chemistry, RWTH Aachen University, Landoltweg 1, D-52074 Aachen, Germany; [email protected] * Correspondence: [email protected]; Tel.: +49-241-80-92075 Received: 17 September 2020; Accepted: 8 October 2020; Published: 10 October 2020 Abstract: Tellurides have attracted an enormous interest in the quest for materials addressing future challenges, because many of them are at the cutting edge of basic research and technologies due to their remarkable chemical and physical properties. The key to the tailored design of tellurides and their properties is a thorough understanding of their electronic structures including the bonding nature. While a unique type of bonding has been recently identified for post-transition-metal tellurides, the electronic structures of tellurides containing early and late-transition-metals have been typically understood by applying the Zintl Klemm concept; yet, does the aforementioned formalism actually − help us in understanding the electronic structures and bonding nature in such tellurides? To answer this question, we prototypically examined the electronic structure for an alkaline metal lanthanide zinc telluride, i.e., RbDyZnTe3, by means of first-principles-based techniques. In this context, the crystal structures of RbLnZnTe3 (Ln = Gd, Tb, Dy),
    [Show full text]
  • Lanthanide Chalcogenolate Complexes: Syntheses, Structures
    中国科技论文在线 http://www.paper.edu.cn Coordination Chemistry Reviews 250 (2006) 2059–2092 Review Lanthanide chalcogenolate complexes: Syntheses, structures and applications in organic chemistry Hong-Xi Li a, Yan-Jun Zhu a, Mei-Ling Cheng a, Zhi-Gang Ren a, Jian-Ping Lang a,b,∗, Qi Shen a a Key Laboratory of Organic Synthesis of Jiangsu Province, School of Chemistry and Engineering, Suzhou University, Suzhou 215123, Jiangsu, PR China b State Key Laboratory of Coordination Chemistry, Nanjing University, Nanjing 210093, Jiangsu, PR China Received 18 October 2005; accepted 9 February 2006 Available online 23 February 2006 Contents 1. Introduction ........................................................................................................... 2060 2. Methods of preparation ................................................................................................. 2060 2.1. Protonolysis reaction ............................................................................................. 2060 2.2. Salt metathesis reaction........................................................................................... 2062 2.3. Oxidation–reduction reaction ..................................................................................... 2063 2.3.1. Oxidation reaction of divalent lanthanocene complexes ...................................................... 2063 2.3.2. Reaction of elemental lanthanide and REER ................................................................ 2065 2.3.3. Reaction of Ln/M amalgam with REER and trans-metallation
    [Show full text]
  • Organic Frameworks Based on 1,2,4,5-Benzenetetracarboxylic
    DESIGN, SYNTHESIS AND APPLICATIONS OF LANTHANIDE METAL- ORGANIC FRAMEWORKS BASED ON 1,2,4,5-BENZENETETRACARBOXYLIC ACID by Joseph William Dixon III A Thesis Submitted to the Faculty of The Charles E. Schmidt College of Science In Partial Fulfillment of the Requirements for the Degree of Master of Science Florida Atlantic University Boca Raton, FL December 2015 Copyright 2015 by Joseph William Dixon III ii ACKNOWLEDGEMENTS Firstly, I acknowledge the Department of Chemistry and Biochemistry accepting me into this program, giving me the opportunity to work with some of the best faculty, professors and researchers around, whom I learned a great deal from. Evelyn Hall and Helena Szczesny are especially thanked for their kindness, helpfulness and overall general support provided to me throughout the past few years. Above all, I express sincere gratitude to my advisor, Dr. Daniel Thomas de Lill for his exceptional patience, motivation and guidance in both my classroom studies and research studies. I’ve learned and acquired so much information/knowledge from him that will without a doubt be helpful to me in my academic endeavors as well as everyday life. In addition, I thank the other two members of my thesis committee, Dr. Deguo Du and Dr. Patricia Snyder for their insightful comments, suggestions and support of my thesis studies. Last but certainly not least, I thank my family and close friends for their love, support and encouragement throughout writing this thesis. Everyone acknowledged helped my dreams become a reality and I am forever grateful. iv ABSTRACT Author: Joseph William Dixon III Title: Design, Synthesis and Applications of Lanthanide Metal-Organic Frameworks based on 1,2,4,5-benzenetetracarboxylic acid Institution: Florida Atlantic University Thesis Advisor: Dr.
    [Show full text]