DOCSLIB.ORG

Contents 1. the Riemann and Lebesgue Integrals. 1 2. the Theory of the Lebesgue Integral

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Contents 1. the Riemann and Lebesgue Integrals. 1 2. the Theory of the Lebesgue Integral Contents 1. The Riemann and Lebesgue integrals. 1 2. The theory of the Lebesgue integral. 7 2.1. The Monotone Convergence Theorem. 7 2.2. Basic theory of Lebesgue integration. 9 2.3. Lebesgue measure. Sets of measure zero. 12 2.4. Nonmeasurable sets. 13 2.5. Lebesgue measurable sets and functions. 14 3. More on the Riemann integral. 18 3.1. The fundamental theorems of calculus. 21 3.2. Characterization of Riemann integrability. 22 1. The Riemann and Lebesgue integrals. Fix a positive integer n. Recall that Rn and Mn are the family of rectangles in Rn and the algebra of multirectangles in Rn, respec- tively. Definition 1.1. We let F + F B n ; n; n; be the set of [0; 1] valued functions on Rn; the vector space of real valued functions n on R ; the vector space of f 2 Fn such that ff =6 0g[rng f is bounded, respectively. We let S B \S M ⊂ F S+ S \F + ⊂ S+ M n = n ( n) n and we let n = n n ( n): n Thus s 2 Sn if and only if s : R ! R, rng s is finite, fs = yg is a multirectangle 2 R f 6 g 2 S+ 2 S ≥ for each y and s = 0 is bounded and s n if and only if s n and s 0. S+ S+ 2 S+ We let n;" be the set of nondecreasing sequences in n . For each s n;" we let 2 F + sup s n be such that n sup s(x) = supfsν (x): ν 2 Ng for x 2 R and we let n f + 2 N+g In;"(s) = sup In (sν ): ν : 2 S+ Remark 1.1. We shall prove below the nontrivial Theorem that if s; t n;" and n n sup s = sup t then In;"(s) = In;"(t). 2 1 2 S+ Proposition 1.1. Suppose c [0; ) and s; t n;". Then 2 S+ n n (i) cs n;" and In;"(cs) = cIn;"(s); 2 n n n n (ii) s + t In;" and In;"(s + t) = In;"(s) + In;"(t); ≤ n ≤ n (iii) if s t then In;"(s) In;"(t). Proof. Straightforward exercise for the reader. □ 1 2 2 F + Definition 1.2. For each f n we let f + 2 S+ ≤ g r(f) = inf In (s): s n and f s and we let f n 2 S+ ≤ g l(f) = inf In;"(s): s n;" and f sup s : Proposition 1.2. We have + 2 S+ r(s) = In (s) whenever s n . Proof. This should be obvious. □ Corollary 1.1. We have jIn(s)j ≤ r(jsj) whenever s 2 Sn. 2 S j j ≤ + j j □ Proof. Indeed, for any s n we have In(s) In ( s ). Remark 1.2. We also have + 2 S+ l(s) = In (s) whenever s n . We shall prove this nontrivial fact shortly. 2 F + 1 2 B Proposition 1.3. Suppose f n and r(f) < . Then f n. 2 S+ ≤ [ f g ⊂ Proof. There is s n such that f s and this implies rng f f > 0 rng s [ fs > 0g. □ 2 Rn 1 2 F + Remark 1.3. On the other hand, if a and f = 1fag n and f = supν ν1fag so l(f) = 0. Proposition 1.4. We have l ≤ r: 2 F + 2 S+ ≤ S+ Proof. Suppose f n , s n and f s. Let t be the sequence in n whose range equals s; that is, tν = s for all ν 2 N. Then sup t = s so ≤ n + l(f) In;"(t) = In (s) + 2 S+ which is to say l(f) is a lower bound for the set of In (u) corresponding to t n with f ≤ t. □ Proposition 1.5. Fn 3 f 7! r(jfj) and Fn 3 f 7! l(jfj) are extended seminorms on Fn. Proof. Straightforward exercise for the reader. □ Example 1.1. Let Q = (0; 1) \ Q: We will show that r(1Q) = 1 and that l(1Q) = 0: ≤ 2 S+ Since 1Q 1(0;1) n we find that ≤ + jj jj r(1Q) In (1(0;1)) = (0; 1) = 1: ≤ 2 + 2 1 Suppose 1Q s In . Let y [0; ]. Obviously, s(x) = s(q) ≥ 1 whenever x 2 s−1[fyg] and q 2 (0; 1) \ Q \ s−1[fyg]. 3 It follows that y ≥ 1 whenever (0; 1) \ int s−1[fyg] =6 ; since, in this case, Q \ s−1[fyg] =6 ;. Therefore, X + jj −1 f g jj In (s) = y s [ y ] 2 y Xrng s = yjjint s−1[fyg]jj 2 y Xrng s ≥ yjj(0; 1) \ int s−1[fyg]jj 2 y Xrng s ≥ jj(0; 1) \ int s−1[fyg]jj 2 y Xrng s = jj(0; 1) \ s−1[fyg]jj y2rng s = 1: Thus r(1Q) ≥ 1: Let q : N ! Q \ [0; 1] be univalent with range Q \ [0; 1]. For each ν 2 N let Xν 2 S+ sν = 1fqµg n : µ=0 2 S+ S+ Note that s n;" is a nondecreasing sequence in n , that Xν + jjf gjj I1 (sν ) = qµ = 0 µ=0 and that 1Q = sup s ≤ sup s: Thus ≤ n l(1Q) In;"(s) = 0: Theorem 1.1. Suppose A 2 Mn, B is a nondecreasing sequence in Mn and ⊂ [1 A ν=0Bν . Then jjAjj ≤ sup jjBν jj: ν + Proof. We define the sequence C in Mn by letting C0 = B0 and for each ν 2 N ∼ [ν 2 N letting Cν = Bν Bν−1. Then C is disjointed and Bν = µ=0Cµ for each ν . Suppose 1 < λ < 1. Choose a compact multirectangle K such that K ⊂ A and jjAjj ≤ λjjKjj. For each ν 2 N choose an open multirectangle Uν such that Cν ⊂ Uν jj jj ≤ jj jj ⊂ [1 2 N ⊂ [N and Uν λ Cν . Then K ν=0Uν so there is N such that K µ=0Uµ. Thus XN XN −1jj jj ≤ jj jj ≤ jj [N jj ≤ jj jj ≤ jj jj jj jj λ A K µ=0 Uµ Uµ λ Cµ = λ BN : µ=0 µ=0 Owing to the arbitrariness of λ the Lemma is proved. □ 4 Corollary 1.2. Suppose A 2 Mn, B is a countable subfamily of Mn and A ⊂ [B. Then X jjAjj ≤ jjBjj: B2B Proof. In case B is finite this follows from earlier work. So suppose B is infinite, B 2 N [ν let B be an enumeration of and, for each ν , let Cν = µ=0Bµ. Then C is a nondecreasing sequence in Mn whose union contains A so that, by the preceding Theorem, Xν X1 jjAjj ≤ sup jjCν jj ≤ sup jjBµjj = jjBν jj: ν ν µ=0 ν=0 □ Theorem 1.2. We have + 2 S+ l(s) = In (s) for any s n . 2 S+ ≤ + Proof. Suppose s n . Obviously, l(s) In (s) S+ ≤ ∼ Suppose t is a nondecreasing sequence in n and s supν tν . Let Y = (rng s) n f0g and for each y 2 Y let Ay = fx 2 R : s(x) = yg. Suppose 0 < λ < 1 and for 2 2 N f 2 g ⊂ [1 each y Y and ν let By,ν = x Ay : λy < tν (y) . Then Ay ν=0By,ν jj jj ≤ jj jj 2 2 N so Ay supν By,ν by the preceding Theorem. For each y Y and ν we have λy1B ≤ 1A tν and this implies that y,ν y ( ) jj jj ≤ jj jj jj jj ≤ λy Ay λy sup B ν = sup λy B ν In 1Ay tν : ν ν Thus X λIn(s) = λyjjAyjj 2 yXY ≤ sup In(1Ay tν ) 2 ν y Y 0 1 X @ A = sup In 1Ay tν ν y2Y ≤ sup In(tν ) Letting λ " 1 we find that In(s) ≤ sup In(tν ). Thus In(s) ≤ l(s). □ Corollary 1.3. We have jIn(s)j ≤ l(jsj) for any s 2 Sn. j j ≤ + j j Proof. This follows from the preceding Theorem since In(s) In ( s ) for any s 2 Sn. □ Definition 1.3. We let Riemn be the set of f 2 Fn such that for each ϵ > 0 there is s 2 Sn such that r(jf −sj) < ϵ. Thus Riemn is the closure of Sn with respect to the extended seminormFn 3 f 7! r(jfj). We say f 2 Fn is Riemann integrable if f 2 Riemn. 5 We let Lebn be the set of f 2 Fn such that for each ϵ > 0 there is s 2 Sn such that l(jf −sj) < ϵ. Thus Lebn is the closure of Sn with respect to the extended seminorm Fn 3 f 7! l(jfj) of Sn. We say f 2 Fn is Lebesgue integrable if f 2 Lebn. Proposition 1.6. Suppose f 2 Fn. Then f 2 Riemn if and only if for each ϵ > 0 there is g 2 Riemn such that r(jf − gj) < ϵ and f 2 Lebn if and only if for each ϵ > 0 there is g 2 Lebn such that r(jf − gj) < ϵ. Proof. This should be obvious. It boils down to the fact the the closure of the closure equals the closure. □ Theorem 1.3. Riemn is a linear subspace of Fn and there is one and only one linear function R : Riemn ! R such that (i) R(s) = In(s) whenever s 2 Sn; (ii) jR(f)j ≤ r(jfj) whenever f 2 Riemn. Lebn is a linear subspace of Fn and there is one and only one linear function L : Lebn ! R such that (i) L(s) = In(s) whenever s 2 Sn; (ii) jL(f)j ≤ l(jfj) whenever f 2 Lebn.
Load more

Recommended publications
  • The Fundamental Theorem of Calculus for Lebesgue Integral
    Divulgaciones Matem´aticasVol. 8 No. 1 (2000), pp. 75{85 The Fundamental Theorem of Calculus for Lebesgue Integral El Teorema Fundamental del C´alculo para la Integral de Lebesgue Di´omedesB´arcenas([email protected]) Departamento de Matem´aticas.Facultad de Ciencias. Universidad de los Andes. M´erida.Venezuela. Abstract In this paper we prove the Theorem announced in the title with- out using Vitali's Covering Lemma and have as a consequence of this approach the equivalence of this theorem with that which states that absolutely continuous functions with zero derivative almost everywhere are constant. We also prove that the decomposition of a bounded vari- ation function is unique up to a constant. Key words and phrases: Radon-Nikodym Theorem, Fundamental Theorem of Calculus, Vitali's covering Lemma. Resumen En este art´ıculose demuestra el Teorema Fundamental del C´alculo para la integral de Lebesgue sin usar el Lema del cubrimiento de Vi- tali, obteni´endosecomo consecuencia que dicho teorema es equivalente al que afirma que toda funci´onabsolutamente continua con derivada igual a cero en casi todo punto es constante. Tambi´ense prueba que la descomposici´onde una funci´onde variaci´onacotada es ´unicaa menos de una constante. Palabras y frases clave: Teorema de Radon-Nikodym, Teorema Fun- damental del C´alculo,Lema del cubrimiento de Vitali. Received: 1999/08/18. Revised: 2000/02/24. Accepted: 2000/03/01. MSC (1991): 26A24, 28A15. Supported by C.D.C.H.T-U.L.A under project C-840-97. 76 Di´omedesB´arcenas 1 Introduction The Fundamental Theorem of Calculus for Lebesgue Integral states that: A function f :[a; b] R is absolutely continuous if and only if it is ! 1 differentiable almost everywhere, its derivative f 0 L [a; b] and, for each t [a; b], 2 2 t f(t) = f(a) + f 0(s)ds: Za This theorem is extremely important in Lebesgue integration Theory and several ways of proving it are found in classical Real Analysis.
    [Show full text]
  • Shape Analysis, Lebesgue Integration and Absolute Continuity Connections
    NISTIR 8217 Shape Analysis, Lebesgue Integration and Absolute Continuity Connections Javier Bernal This publication is available free of charge from: https://doi.org/10.6028/NIST.IR.8217 NISTIR 8217 Shape Analysis, Lebesgue Integration and Absolute Continuity Connections Javier Bernal Applied and Computational Mathematics Division Information Technology Laboratory This publication is available free of charge from: https://doi.org/10.6028/NIST.IR.8217 July 2018 INCLUDES UPDATES AS OF 07-18-2018; SEE APPENDIX U.S. Department of Commerce Wilbur L. Ross, Jr., Secretary National Institute of Standards and Technology Walter Copan, NIST Director and Undersecretary of Commerce for Standards and Technology ______________________________________________________________________________________________________ This Shape Analysis, Lebesgue Integration and publication Absolute Continuity Connections Javier Bernal is National Institute of Standards and Technology, available Gaithersburg, MD 20899, USA free of Abstract charge As shape analysis of the form presented in Srivastava and Klassen’s textbook “Functional and Shape Data Analysis” is intricately related to Lebesgue integration and absolute continuity, it is advantageous from: to have a good grasp of the latter two notions. Accordingly, in these notes we review basic concepts and results about Lebesgue integration https://doi.org/10.6028/NIST.IR.8217 and absolute continuity. In particular, we review fundamental results connecting them to each other and to the kind of shape analysis, or more generally, functional data analysis presented in the aforeme- tioned textbook, in the process shedding light on important aspects of all three notions. Many well-known results, especially most results about Lebesgue integration and some results about absolute conti- nuity, are presented without proofs.
    [Show full text]
  • An Introduction to Measure Theory Terence
    An introduction to measure theory Terence Tao Department of Mathematics, UCLA, Los Angeles, CA 90095 E-mail address: [email protected] To Garth Gaudry, who set me on the road; To my family, for their constant support; And to the readers of my blog, for their feedback and contributions. Contents Preface ix Notation x Acknowledgments xvi Chapter 1. Measure theory 1 x1.1. Prologue: The problem of measure 2 x1.2. Lebesgue measure 17 x1.3. The Lebesgue integral 46 x1.4. Abstract measure spaces 79 x1.5. Modes of convergence 114 x1.6. Differentiation theorems 131 x1.7. Outer measures, pre-measures, and product measures 179 Chapter 2. Related articles 209 x2.1. Problem solving strategies 210 x2.2. The Radamacher differentiation theorem 226 x2.3. Probability spaces 232 x2.4. Infinite product spaces and the Kolmogorov extension theorem 235 Bibliography 243 vii viii Contents Index 245 Preface In the fall of 2010, I taught an introductory one-quarter course on graduate real analysis, focusing in particular on the basics of mea- sure and integration theory, both in Euclidean spaces and in abstract measure spaces. This text is based on my lecture notes of that course, which are also available online on my blog terrytao.wordpress.com, together with some supplementary material, such as a section on prob- lem solving strategies in real analysis (Section 2.1) which evolved from discussions with my students. This text is intended to form a prequel to my graduate text [Ta2010] (henceforth referred to as An epsilon of room, Vol. I ), which is an introduction to the analysis of Hilbert and Banach spaces (such as Lp and Sobolev spaces), point-set topology, and related top- ics such as Fourier analysis and the theory of distributions; together, they serve as a text for a complete first-year graduate course in real analysis.
    [Show full text]
  • Definition of Riemann Integrals
    The Definition and Existence of the Integral Definition of Riemann Integrals Definition (6.1) Let [a; b] be a given interval. By a partition P of [a; b] we mean a finite set of points x0; x1;:::; xn where a = x0 ≤ x1 ≤ · · · ≤ xn−1 ≤ xn = b We write ∆xi = xi − xi−1 for i = 1;::: n. The Definition and Existence of the Integral Definition of Riemann Integrals Definition (6.1) Now suppose f is a bounded real function defined on [a; b]. Corresponding to each partition P of [a; b] we put Mi = sup f (x)(xi−1 ≤ x ≤ xi ) mi = inf f (x)(xi−1 ≤ x ≤ xi ) k X U(P; f ) = Mi ∆xi i=1 k X L(P; f ) = mi ∆xi i=1 The Definition and Existence of the Integral Definition of Riemann Integrals Definition (6.1) We put Z b fdx = inf U(P; f ) a and we call this the upper Riemann integral of f . We also put Z b fdx = sup L(P; f ) a and we call this the lower Riemann integral of f . The Definition and Existence of the Integral Definition of Riemann Integrals Definition (6.1) If the upper and lower Riemann integrals are equal then we say f is Riemann-integrable on [a; b] and we write f 2 R. We denote the common value, which we call the Riemann integral of f on [a; b] as Z b Z b fdx or f (x)dx a a The Definition and Existence of the Integral Left and Right Riemann Integrals If f is bounded then there exists two numbers m and M such that m ≤ f (x) ≤ M if (a ≤ x ≤ b) Hence for every partition P we have m(b − a) ≤ L(P; f ) ≤ U(P; f ) ≤ M(b − a) and so L(P; f ) and U(P; f ) both form bounded sets (as P ranges over partitions).
    [Show full text]
  • Generalizations of the Riemann Integral: an Investigation of the Henstock Integral
    Generalizations of the Riemann Integral: An Investigation of the Henstock Integral Jonathan Wells May 15, 2011 Abstract The Henstock integral, a generalization of the Riemann integral that makes use of the δ-fine tagged partition, is studied. We first consider Lebesgue’s Criterion for Riemann Integrability, which states that a func- tion is Riemann integrable if and only if it is bounded and continuous almost everywhere, before investigating several theoretical shortcomings of the Riemann integral. Despite the inverse relationship between integra- tion and differentiation given by the Fundamental Theorem of Calculus, we find that not every derivative is Riemann integrable. We also find that the strong condition of uniform convergence must be applied to guarantee that the limit of a sequence of Riemann integrable functions remains in- tegrable. However, by slightly altering the way that tagged partitions are formed, we are able to construct a definition for the integral that allows for the integration of a much wider class of functions. We investigate sev- eral properties of this generalized Riemann integral. We also demonstrate that every derivative is Henstock integrable, and that the much looser requirements of the Monotone Convergence Theorem guarantee that the limit of a sequence of Henstock integrable functions is integrable. This paper is written without the use of Lebesgue measure theory. Acknowledgements I would like to thank Professor Patrick Keef and Professor Russell Gordon for their advice and guidance through this project. I would also like to acknowledge Kathryn Barich and Kailey Bolles for their assistance in the editing process. Introduction As the workhorse of modern analysis, the integral is without question one of the most familiar pieces of the calculus sequence.
    [Show full text]
  • Worked Examples on Using the Riemann Integral and the Fundamental of Calculus for Integration Over a Polygonal Element Sulaiman Abo Diab
    Worked Examples on Using the Riemann Integral and the Fundamental of Calculus for Integration over a Polygonal Element Sulaiman Abo Diab To cite this version: Sulaiman Abo Diab. Worked Examples on Using the Riemann Integral and the Fundamental of Calculus for Integration over a Polygonal Element. 2019. hal-02306578v1 HAL Id: hal-02306578 https://hal.archives-ouvertes.fr/hal-02306578v1 Preprint submitted on 6 Oct 2019 (v1), last revised 5 Nov 2019 (v2) HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Worked Examples on Using the Riemann Integral and the Fundamental of Calculus for Integration over a Polygonal Element Sulaiman Abo Diab Faculty of Civil Engineering, Tishreen University, Lattakia, Syria [email protected] Abstracts: In this paper, the Riemann integral and the fundamental of calculus will be used to perform double integrals on polygonal domain surrounded by closed curves. In this context, the double integral with two variables over the domain is transformed into sequences of single integrals with one variable of its primitive. The sequence is arranged anti clockwise starting from the minimum value of the variable of integration. Finally, the integration over the closed curve of the domain is performed using only one variable.
    [Show full text]
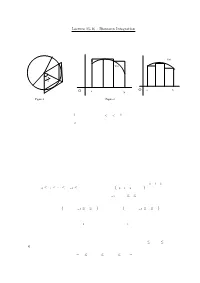
  • Lecture 15-16 : Riemann Integration Integration Is Concerned with the Problem of finding the Area of a Region Under a Curve
    1 Lecture 15-16 : Riemann Integration Integration is concerned with the problem of ¯nding the area of a region under a curve. Let us start with a simple problem : Find the area A of the region enclosed by a circle of radius r. For an arbitrary n, consider the n equal inscribed and superscibed triangles as shown in Figure 1. f(x) f(x) π 2 n O a b O a b Figure 1 Figure 2 Since A is between the total areas of the inscribed and superscribed triangles, we have nr2sin(¼=n)cos(¼=n) · A · nr2tan(¼=n): By sandwich theorem, A = ¼r2: We will use this idea to de¯ne and evaluate the area of the region under a graph of a function. Suppose f is a non-negative function de¯ned on the interval [a; b]: We ¯rst subdivide the interval into a ¯nite number of subintervals. Then we squeeze the area of the region under the graph of f between the areas of the inscribed and superscribed rectangles constructed over the subintervals as shown in Figure 2. If the total areas of the inscribed and superscribed rectangles converge to the same limit as we make the partition of [a; b] ¯ner and ¯ner then the area of the region under the graph of f can be de¯ned as this limit and f is said to be integrable. Let us de¯ne whatever has been explained above formally. The Riemann Integral Let [a; b] be a given interval. A partition P of [a; b] is a ¯nite set of points x0; x1; x2; : : : ; xn such that a = x0 · x1 · ¢ ¢ ¢ · xn¡1 · xn = b.
    [Show full text]
  • Computing the Bayes Factor from a Markov Chain Monte Carlo
    Computing the Bayes Factor from a Markov chain Monte Carlo Simulation of the Posterior Distribution Martin D. Weinberg∗ Department of Astronomy University of Massachusetts, Amherst, USA Abstract Computation of the marginal likelihood from a simulated posterior distribution is central to Bayesian model selection but is computationally difficult. The often-used harmonic mean approximation uses the posterior directly but is unstably sensitive to samples with anomalously small values of the likelihood. The Laplace approximation is stable but makes strong, and of- ten inappropriate, assumptions about the shape of the posterior distribution. It is useful, but not general. We need algorithms that apply to general distributions, like the harmonic mean approximation, but do not suffer from convergence and instability issues. Here, I argue that the marginal likelihood can be reliably computed from a posterior sample by careful attention to the numerics of the probability integral. Posing the expression for the marginal likelihood as a Lebesgue integral, we may convert the harmonic mean approximation from a sample statistic to a quadrature rule. As a quadrature, the harmonic mean approximation suffers from enor- mous truncation error as consequence . This error is a direct consequence of poor coverage of the sample space; the posterior sample required for accurate computation of the marginal likelihood is much larger than that required to characterize the posterior distribution when us- ing the harmonic mean approximation. In addition, I demonstrate that the integral expression for the harmonic-mean approximation converges slowly at best for high-dimensional problems with uninformative prior distributions. These observations lead to two computationally-modest families of quadrature algorithms that use the full generality sample posterior but without the instability.
    [Show full text]
  • Problem Set 6
    Richard Bamler Jeremy Leach office 382-N, phone: 650-723-2975 office 381-J [email protected] [email protected] office hours: office hours: Mon 1:00pm-3pm, Thu 1:00pm-2:00pm Thu 3:45pm-6:45pm MATH 172: Lebesgue Integration and Fourier Analysis (winter 2012) Problem set 6 due Wed, 2/22 in class (1) (20 points) Let X be an arbitrary space, M a σ-algebra on X and λ a measure on M. Consider an M-measurable function ρ : X ! [0; 1] which only takes non-negative values. (a) Show that the function, Z µ : M! [0; 1];A 7! (ρχA)dλ is a measure on M. We will also denote this measure by µ = (ρλ). (b) Show that any M-measurable function f : X ! R is integrable with respect to µ if and only if fρ is integrable with respect to λ. In this case we have Z Z Z fdµ = fd(ρλ) = fρdλ. (Hint: Show first that this is true for simple functions, then for non-negative functions, then for general functions). (c) Show that if A 2 M is a nullset with respect to λ, then it is also a nullset with respect to µ = ρλ. (Remark: A measure µ with this property is called absolutely continuous with respect to λ in symbols µ λ.) (d) Assume that X = Rn, M = L and λ is the Lebesgue measure. Give an example for a measure µ0 on M such that there is no non-negative, M- measurable function ρ : X ! [0; 1] with µ0 = ρλ.
    [Show full text]
  • Intuitive Mathematical Discourse About the Complex Path Integral Erik Hanke
    Intuitive mathematical discourse about the complex path integral Erik Hanke To cite this version: Erik Hanke. Intuitive mathematical discourse about the complex path integral. INDRUM 2020, Université de Carthage, Université de Montpellier, Sep 2020, Cyberspace (virtually from Bizerte), Tunisia. hal-03113845 HAL Id: hal-03113845 https://hal.archives-ouvertes.fr/hal-03113845 Submitted on 18 Jan 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Intuitive mathematical discourse about the complex path integral Erik Hanke1 1University of Bremen, Faculty of Mathematics and Computer Science, Germany, [email protected] Interpretations of the complex path integral are presented as a result from a multi-case study on mathematicians’ intuitive understanding of basic notions in complex analysis. The first case shows difficulties of transferring the image of the integral in real analysis as an oriented area to the complex setting, and the second highlights the complex path integral as a tool in complex analysis with formal analogies to path integrals in multivariable calculus. These interpretations are characterised as a type of intuitive mathematical discourse and the examples are analysed from the point of view of substantiation of narratives within the commognitive framework.
    [Show full text]
  • General Riemann Integrals and Their Computation Via Domain
    Louisiana State University LSU Digital Commons LSU Historical Dissertations and Theses Graduate School 1999 General Riemann Integrals and Their omputC ation via Domain. Bin Lu Louisiana State University and Agricultural & Mechanical College Follow this and additional works at: https://digitalcommons.lsu.edu/gradschool_disstheses Recommended Citation Lu, Bin, "General Riemann Integrals and Their omputC ation via Domain." (1999). LSU Historical Dissertations and Theses. 7001. https://digitalcommons.lsu.edu/gradschool_disstheses/7001 This Dissertation is brought to you for free and open access by the Graduate School at LSU Digital Commons. It has been accepted for inclusion in LSU Historical Dissertations and Theses by an authorized administrator of LSU Digital Commons. For more information, please contact [email protected]. INFORMATION TO USERS This manuscript has been reproduced from the microfilm master. UMI films the text directly from the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while others may be from any type of computer printer. The quality of this reproduction is dependent upon the quality of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, phnt bleedthrough, substandard margins, and improper alignment can adversely affect reproduction. In the unlikely event that the author did not send UMI a complete manuscript and there are missing pages, these will be noted. Also, if unauthorized copyright material had to be removed, a note will indicate the deletion. Oversize materials (e.g., maps, drawings, charts) are reproduced by sectioning the original, beginning at the upper left-hand comer and continuing from left to right in equal sections with small overlaps.
    [Show full text]
  • More Information About Line and Contour Integrals
    More information about line and contour integrals. Real line integrals. Let P (x, y)andQ(x, y) be continuous real valued functions on the plane and let γ be a smooth directed curve. We wish to define the line integral Z P (x, y) dx + Q(x, y) dy. γ This can be done in several ways. One of which is to partition the curve γ by a very large number of points, define Riemann sums for the partition, and then take a limit as the “mesh” of the partition gets finer and finer. However an argument like the one we did in class for complex line integrals shows that if c(t)=(x(t),y(t)) with a ≤ t ≤ b is a smooth parameterization of γ then Z Z b P (x, y) dx + Q(x, y) dy = P (x(t),y(t))x0(t)+Q(x(t),y(t)) dt. γ a R This reduces computing γ P (x, y) dx + Q(x, y) dy to first finding a parameterization of γ and then computing a standard Riemann integral such as we have all seen in calculus. Here is an example. Let γ be the upper half of the circle |z| =1 transversed counter clockwise. Then compute Z (1) xy2 dx − (x + y + x3y) dy. γ This half circle is parameterized by x(t)=cos(t),y(t)=sin(t) with 0 ≤ t ≤ π. Now the calculation proceeds just as if we were doing a change of variables. That is dx = − sin(t) dt, dy = cos(t) dt 1 2 Using these formulas in (1) gives Z xy2 dx − (x + y + x3y) dy γ Z π = cos(t)sin2(t)(− sin(t)) dt − (cos(t)+sin(t)+cos3(t)sin(t)) cos(t) dt Z0 π = cos(t)sin2(t)(− sin(t)) − (cos(t)+sin(t)+cos3(t)sin(t)) cos(t) dt 0 With a little work1 this can be shown to have the value −(2/5+π/2).
    [Show full text]