DOCSLIB.ORG

Ed 040 737 Institution Available from Edrs Price

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Ed 040 737 Institution Available from Edrs Price DOCUMENT RESUME ED 040 737 LI 002 060 TITLE Automatic Data Processing Glossary. INSTITUTION Bureau of the Budget, Washington, D.C. NOTE 65p. AVAILABLE FROM Reprinted and distributed by Datamation Magazine, 35 Mason St., Greenwich, Conn. 06830 ($1.00) EDRS PRICE EDRS Price MF-$0.50 HC-$3.35 DESCRIPTORS *Electronic Data Processing, *Glossaries, *Word Lists ABSTRACT The technology of the automatic information processing field has progressed dramatically in the past few years and has created a problem in common term usage. As a solution, "Datamation" Magazine offers this glossary which was compiled by the U.S. Bureau of the Budget as an official reference. The terms appear in a single alphabetic sequence, ignoring commas or hyphens. Definitions are given only under "key word" entries. Modifiers consisting of more than one word are listed in the normally used sequence (record, fixed length). In cases where two or more terms have the same meaning, only the preferred term is defined, all synonylious terms are given at the end of the definition.Other relationships between terms are shown by descriptive referencing expressions. Hyphens are used sparingly to avoid ambiguity. The derivation of an acronym is shown by underscoring the appropriate letters in the words from which the acronym is formed. Although this glossary is several years old, it is still considered the best one available. (NH) Ns U.S DEPARTMENT OF HEALTH, EDUCATION & WELFARE OFFICE OF EDUCATION THIS DOCUMENT HAS BEEN REPRODUCED EXACTLY AS RECEIVED FROM THE PERSON OR ORGANIZATION ORIGINATING IT POINTS OF VIEW OR OPINIONS STATED DO NOT NECES- SARILY REPRESENT OFFICIAL OFFICE OF EDU- CATION POSITION OR POLICY automatic data processing GLOSSA 1 I.R DATAMATION Magazine reprints this Glossary of Terms as a service to the data processing field. As with any new and dynamic field, standardization and common terminology are generally after- thoughts: The technology of the automatic information processing field has progressed dramatically in the past few years and now is the time that we should address ourselves to the problem of common terms. Towards this end we offer this glossary, which was compiled by the i U. S. Bureau of the Budget as an official reference. Although sev- eral years old, it is to our knowledge the best glossary available. It is our hope that this will contribute to a greater interchange of information and standardization within this vastly expanding field. GARDNER F. LANDON Publisher A GUIDE TO USERS 1.Typography and General Format. Terms in this glossary appear in a single alphabetic sequence, ignoring commas or hyphens. Lower case, bold characters are used for terms, except acronyms and the initial letters of proper nouns, for which capital, bold letters are used. Lighter facecharacters are used for definitions and for cross referencing or clarifying terms. 2.Key Words and Modifiers. Definitions are given only under key word entries. Such entries may be either single word or multiple word terms, and may be nouns or other parts of speech. For example: address (noun) address, direct (noun, multiple term) algorithmic (adjective) assemble (verb) auto-abstract (noun; verb) Modifiers consisting of more than one word are listed in spoken or normally used sequence. For example: program, internally stored record, fixed length 3.Preferred Terminology. When two or more terms have the same meaning, definitions are given only under the preferred term. The phrase, "same as ..." is used to indicate the term under which the definition appears. For example: quantizer, same as (digitizer). All synonymous terms are given at the end of the definition. For example: digitizer, a device which converts an analog measurement into digital form, Synony- mous with (quantizer). 4.Cross Referencing. Other relationships_ between terms are shown by descriptive referencing expressions. The following are examples; similar to, contrasted with,.and clarified by. The expression "see ...", is used only with terms appearing in an inverted word order, and serves to lead the user to the term where the definition appears. 5.Use of Hyphens. Hyphens have been used sparingly, and chiefly to avoid ambiguity. For example, in the term "data-reduction", the hyphen indicates that the term is a single concept and does not appear in the inverted word form. 6.Acronyms. The derivation of an acronym is shown by underscoring the appropriate letters in the words from whiCh the acronym is formed. For example: COBOL, Common Business Oriented Language. ii A as long as the input signals are present. Re- lated to (accumulator) (2). absolute address, see (address, absolute). address, (1) an identification, represented by absolute code, see (code, absolute). a name, label or number, for a register or absolute error, see (error, absolute). location in storage. Addresses are also a absolute value computer, see (computer, abso- part of an instruction word along with com- lute value). mands, tags, and other symbols. (2) The part a. c. dump, see (dump, a. c.). of an instruction which specifies an operand acceleration time, see (time, acceleration). for the 'instruction. access, immediate, pertaining to the ability to address, absolute, an address which indicates obtain data from or place data in a storage the exact storage location where the ref. device, or register directly without serial erenced operand is to be found or stored in delay due to other units of data, and usually the actual machine code address numbering in a relatively short period of time. system. Synonymous with (specific address) access, parallel, the process of obtaining in- and related to (code, absolute). formation from or placing information into address, base, (1) a number which appears as storage where the time required for such an address in a computer instruction, but access isdependent on the simultaneous which serves as the base, index, initial or transfer of all elements of a word from a starting point for subsequent addresses to be given stor a ge location. Synonymous with m o d i f i e d. Synonymous with (presumptive (simultaneous access). address) and (reference address). (2) A num- access, random, (1) pertaining to the process ber used in symbolic coding in conjunction ofobtaining information from or placing with a relative address. information into storage where the time re- address, direct, an address which indicates the quired for such access is independent of the location where the referenced operand is to location of the information most recently ob- be found or stored with no reference to an tained or placed in storage; (2) pertaining to index register or B-Box. Synonymous with a device in which random access, as defined (first level address). in definition 1, can be achieved without ef- address, effective, (1) a modified address. fective penalty in time. (2) The address actually considered to be access, serial, pertainingtothe process of used in a particular execution of a computer obtaining information from or placing infor- instruction. mation into storage where the time required address, first level, same as (address, direct). for such access is dependent on the necessity address, floating, formerly, an address written for waiting while nondesired storage locations in such a way that it can easily be converted are processed in turn. to a machine address by indexing, assembly, access, simultaneous, sameas(access, or by some other means. parallel). address, four, a method of specifying the loca- access, time,see (time, access.). tion of operands and instructions in which the accounting machine, same as (tabulator). storage location of the two operands and the accumulator, (1) theregister and associated storage location of the results of the opera- equipment in the arithmetic unit of the com- tion are cited, and the storage location of the puter in which arithmetical and logical op- next instruction to be executed are cited. erations are performed. (2) A unit in a digital address, immediate, an instruction address in computer where numbers are totaled; i.e., which the address part of the instruction is accumulated. Often the accumulator stores theoperand. Synonymous with (zero level 11 one operand and upon receipt of .any second address). operand, it forms and stores the result of address, indexed, an address thatisto be performing the indicated operation on the modified or has been modified by an index first and second operands. Related to (adder). register or similar device. Synonymous with fJ accuracy, the degree of exactness of an ap- (variable address). proximation or measurement. High accuracy address, indirect, an address in a computer fi thus implies low error. Accuracy normally instruction which indicates a location where denotes absolute quality of computed results; the address of the referenced operand is to precision usually refers to the amount of de- be found. In some computers the machine tail used in representing those results. Thus, address indicated can itself be indirect. Such four place results are less precise than six multiple levels of addressing are terminated place results; nevertheless a four place table either by prior control or by a termination might be more accurate than an erroneously s ymb o 1. Synonymous with(second level computed six place table. address). acoustic delay line, see (line, acoustic delay). address, machine, an absolute, direct, unin- action, rate, a type of control action in which dexed address expressed as such, or result- the rate of correction is made proportionalto ing after indexing and other processing has how fast the condition is going awry. This is been completed. also called derivative action. address, multi, same as (address, multiple). add subtract time, see (time, add subtract). address, multiple, a type of instruction which adder, a device which forms, as output, the specifies the addresses of two or more items sum of two, or more numbers presented as which may be the addresses of locations of inputs.
Load more

Recommended publications
  • Dynamical Directions in Numeration Tome 56, No 7 (2006), P
    R AN IE N R A U L E O S F D T E U L T I ’ I T N S ANNALES DE L’INSTITUT FOURIER Guy BARAT, Valérie BERTHÉ, Pierre LIARDET & Jörg THUSWALDNER Dynamical directions in numeration Tome 56, no 7 (2006), p. 1987-2092. <http://aif.cedram.org/item?id=AIF_2006__56_7_1987_0> © Association des Annales de l’institut Fourier, 2006, tous droits réservés. L’accès aux articles de la revue « Annales de l’institut Fourier » (http://aif.cedram.org/), implique l’accord avec les conditions générales d’utilisation (http://aif.cedram.org/legal/). Toute re- production en tout ou partie cet article sous quelque forme que ce soit pour tout usage autre que l’utilisation à fin strictement per- sonnelle du copiste est constitutive d’une infraction pénale. Toute copie ou impression de ce fichier doit contenir la présente mention de copyright. cedram Article mis en ligne dans le cadre du Centre de diffusion des revues académiques de mathématiques http://www.cedram.org/ Ann. Inst. Fourier, Grenoble 56, 7 (2006) 1987-2092 DYNAMICAL DIRECTIONS IN NUMERATION by Guy BARAT, Valérie BERTHÉ, Pierre LIARDET & Jörg THUSWALDNER (*) Abstract. — This survey aims at giving a consistent presentation of numer- ation from a dynamical viewpoint: we focus on numeration systems, their asso- ciated compactification, and dynamical systems that can be naturally defined on them. The exposition is unified by the fibred numeration system concept. Many examples are discussed. Various numerations on rational integers, real or complex numbers are presented with special attention paid to β-numeration and its gener- alisations, abstract numeration systems and shift radix systems, as well as G-scales and odometers.
    [Show full text]
  • High Performance Decimal Floating-Point Units
    UNIVERSIDADE DE SANTIAGO DE COMPOSTELA DEPARTAMENTO DE ELECTRONICA´ E COMPUTACION´ PhD. Dissertation High-Performance Decimal Floating-Point Units Alvaro´ Vazquez´ Alvarez´ Santiago de Compostela, January 2009 To my family A´ mina˜ familia Acknowledgements It has been a long way to see this thesis successfully concluded, at least longer than what I imagined it. Perhaps the moment to thank and acknowledge everyone’s contributions is the most eagerly awaited. This thesis could not have been possible without the support of several people and organizations whose contributions I am very grateful. First of all, I want to express my sincere gratitude to my thesis advisor, Elisardo Antelo. Specially, I would like to emphasize the invaluable support he offered to me all these years. His ideas and contributions have a major influence on this thesis. I would like to thank all people in the Departamento de Electronica´ e Computacion´ for the material and personal help they gave me to carry out this thesis, and for providing a friendly place to work. In particular, I would like to mention to Prof. Javier D. Bruguera and the other staff of the Computer Architecture Group. Many thanks to Paula, David, Pichel, Marcos, Juanjo, Oscar,´ Roberto and my other workmates for their friendship and help. I am very grateful to IBM Germany for their financial support though a one-year research contract. I would like to thank Ralf Fischer, lead of hardware development, and Peter Roth and Stefan Wald, team managers at IBM Deutchland Entwicklung in Boblingen.¨ I would like to extend my gratitude to the FPU design team, in special to Silvia Muller¨ and Michael Kroner,¨ for their help and the warm welcome I received during my stay in Boblingen.¨ I would also like to thank Eric Schwarz from IBM for his support.
    [Show full text]
  • Fully Redundant Decimal Arithmetic
    2009 19th IEEE International Symposium on Computer Arithmetic Fully Redundant Decimal Arithmetic Saeid Gorgin and Ghassem Jaberipur Dept. of Electrical & Computer Engr., Shahid Beheshti Univ. and School of Computer Science, institute for research in fundamental sciences (IPM), Tehran, Iran [email protected], [email protected] Abstract In both decimal and binary arithmetic, partial products in multipliers and partial remainders in Hardware implementation of all the basic radix-10 dividers are often represented via a redundant number arithmetic operations is evolving as a new trend in the system (e.g., Binary signed digit [11], decimal carry- design and implementation of general purpose digital save [5], double-decimal [6], and minimally redundant processors. Redundant representation of partial decimal [9]). Such use of redundant digit sets, where products and remainders is common in the the number of digits is sufficiently more than the radix, multiplication and division hardware algorithms, allows for carry-free addition and subtraction as the respectively. Carry-free implementation of the more basic operations that build-up the product and frequent add/subtract operations, with the byproduct of remainder, respectively. In the aforementioned works enhancing the speed of multiplication and division, is on decimal multipliers and dividers, inputs and outputs possible with redundant number representation. are nonredundant decimal numbers. However, a However, conversion of redundant results to redundant representation is used for the intermediate conventional representations entails slow carry partial products or remainders. The intermediate propagation that can be avoided if the results are kept additions and subtractions are semi-redundant in redundant format for later use as operands of other operations in that only one of the operands as well as arithmetic operations.
    [Show full text]
  • Basic Computer Arithmetic
    BASIC COMPUTER ARITHMETIC TSOGTGEREL GANTUMUR Abstract. First, we consider how integers and fractional numbers are represented and manipulated internally on a computer. The focus is on the principles behind the algorithms, rather than on implementation details. Then we develop a basic theoretical framework for analyzing algorithms involving inexact arithmetic. Contents 1. Introduction 1 2. Integers 2 3. Simple division algorithms 6 4. Long division 11 5. The SRT division algorithm 16 6. Floating point numbers 18 7. Floating point arithmetic 21 8. Propagation of error 24 9. Summation and product 29 1. Introduction There is no way to encode all real numbers by using finite length words, even if we use an alphabet with countably many characters, because the set of finite sequences of integers is countable. Fortunately, the real numbers support many countable dense subsets, and hence the encoding problem of real numbers may be replaced by the question of choosing a suitable countable dense subset. Let us look at some practical examples of real number encodings. ● Decimal notation. Examples: 36000, 2:35(75), −0:000072. ● Scientific notation. Examples: 3:6⋅104, −72⋅10−6. The general form is m⋅10e. In order to have a unique (or near unique) representation of each number, one can impose a normalization, such as requiring 1 ≤ ∣m∣ < 10. 2 −1 ● System with base/radix β. Example: m2m1m0:m−1 = m2β +m1β +m0 +m−1β . The dot separating the integer and fractional parts is called the radix point. ● Binary (β = 2), octal (β = 8), and hexadecimal (β = 16) numbers. ● Babylonian hexagesimal (β = 60) numbers.
    [Show full text]
  • Algorithms and Architectures for Decimal Transcendental Function Computation
    Algorithms and Architectures for Decimal Transcendental Function Computation A Thesis Submitted to the College of Graduate Studies and Research in Partial Fulfillment of the Requirements for the degree of Doctor of Philosophy in the Department of Electrical and Computer Engineering University of Saskatchewan Saskatoon, Saskatchewan, Canada By Dongdong Chen c Dongdong Chen, January, 2011. All rights reserved. Permission to Use In presenting this thesis in partial fulfilment of the requirements for a Postgraduate degree from the University of Saskatchewan, I agree that the Libraries of this University may make it freely available for inspection. I further agree that permission for copying of this thesis in any manner, in whole or in part, for scholarly purposes may be granted by the professor or professors who supervised my thesis work or, in their absence, by the Head of the Department or the Dean of the College in which my thesis work was done. It is understood that any copying or publication or use of this thesis or parts thereof for financial gain shall not be allowed without my written permission. It is also understood that due recognition shall be given to me and to the University of Saskatchewan in any scholarly use which may be made of any material in my thesis. Requests for permission to copy or to make other use of material in this thesis in whole or part should be addressed to: Head of the Department of Electrical and Computer Engineering 57 Campus Drive University of Saskatchewan Saskatoon, Saskatchewan Canada S7N 5A9 i Abstract Nowadays, there are many commercial demands for decimal floating-point (DFP) arith- metic operations such as financial analysis, tax calculation, currency conversion, Internet based applications, and e-commerce.
    [Show full text]
  • History of Binary and Other Nondecimal Numeration
    HISTORY OF BINARY AND OTHER NONDECIMAL NUMERATION BY ANTON GLASER Professor of Mathematics, Pennsylvania State University TOMASH PUBLISHERS Copyright © 1971 by Anton Glaser Revised Edition, Copyright 1981 by Anton Glaser All rights reserved Printed in the United States of America Library of Congress Cataloging in Publication Data Glaser, Anton, 1924- History of binary and other nondecimal numeration. Based on the author's thesis (Ph. D. — Temple University), presented under the title: History of modern numeration systems. Bibliography: p. 193 Includes Index. 1. Numeration — History. I. Title QA141.2.G55 1981 513'.5 81-51176 ISBN 0-938228-00-5 AACR2 To My Wife, Ruth ACKNOWLEDGMENTS THIS BOOK is based on the author’s doctoral dissertation, History of Modern Numeration Systems, written under the guidance of Morton Alpren, Sara A. Rhue, and Leon Steinberg of Temple University in Philadelphia, Pa. Extensive help was received from the libraries of the Academy of the New Church (Bryn Athyn, Pa.), the American Philosophical Society, Pennsylvania State University, Temple University, the University of Michigan, and the University of Pennsylvania. The photograph of Figure 7 was made available by the New York Public Library; the library of the University of Pennsylvania is the source of the photographs in Figures 2 and 6. The author is indebted to Harold Hanes, Joseph E. Hofmann, Donald E. Knuth, and Brian J. Winkel, who were kind enough to communicate their comments about the strengths and weaknesses of the original edition. The present revised edition is the better for it. A special thanks is also owed to John Wagner for his careful editorial work and to Adele Clark for her thorough preparation of the Index.
    [Show full text]
  • The Mayan Long Count Calendar Thomas Chanier
    The Mayan Long Count Calendar Thomas Chanier To cite this version: Thomas Chanier. The Mayan Long Count Calendar. 2015. hal-00750006v11 HAL Id: hal-00750006 https://hal.archives-ouvertes.fr/hal-00750006v11 Preprint submitted on 8 Dec 2015 (v11), last revised 16 Dec 2015 (v12) HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. The Mayan Long Count Calendar Thomas Chanier∗1 1 Universit´ede Brest, 6 avenue Victor le Gorgeu, F-29285 Brest Cedex, France The Mayan Codices, bark-paper books from the Late Postclassic period (1300 to 1521 CE) contain many astronomical tables correlated to ritual cycles, evidence of the achievement of Mayan naked- eye astronomy and mathematics in connection to religion. In this study, a calendar supernumber is calculated by computing the least common multiple of 8 canonical astronomical periods. The three major calendar cycles, the Calendar Round, the Kawil and the Long Count Calendar are shown to derive from this supernumber. The 360-day Tun, the 365-day civil year Haab’ and the 3276-day Kawil-direction-color cycle are determined from the prime factorization of the 8 canonical astronomical input parameters.
    [Show full text]
  • Non-Power Positional Number Representation Systems, Bijective Numeration, and the Mesoamerican Discovery of Zero
    Non-Power Positional Number Representation Systems, Bijective Numeration, and the Mesoamerican Discovery of Zero Berenice Rojo-Garibaldia, Costanza Rangonib, Diego L. Gonz´alezb;c, and Julyan H. E. Cartwrightd;e a Posgrado en Ciencias del Mar y Limnolog´ıa, Universidad Nacional Aut´onomade M´exico, Av. Universidad 3000, Col. Copilco, Del. Coyoac´an,Cd.Mx. 04510, M´exico b Istituto per la Microelettronica e i Microsistemi, Area della Ricerca CNR di Bologna, 40129 Bologna, Italy c Dipartimento di Scienze Statistiche \Paolo Fortunati", Universit`adi Bologna, 40126 Bologna, Italy d Instituto Andaluz de Ciencias de la Tierra, CSIC{Universidad de Granada, 18100 Armilla, Granada, Spain e Instituto Carlos I de F´ısicaTe´oricay Computacional, Universidad de Granada, 18071 Granada, Spain Keywords: Zero | Maya | Pre-Columbian Mesoamerica | Number rep- resentation systems | Bijective numeration Abstract Pre-Columbian Mesoamerica was a fertile crescent for the development of number systems. A form of vigesimal system seems to have been present from the first Olmec civilization onwards, to which succeeding peoples made contributions. We discuss the Maya use of the representational redundancy present in their Long Count calendar, a non-power positional number representation system with multipliers 1, 20, 18× 20, :::, 18× arXiv:2005.10207v2 [math.HO] 23 Mar 2021 20n. We demonstrate that the Mesoamericans did not need to invent positional notation and discover zero at the same time because they were not afraid of using a number system in which the same number can be written in different ways. A Long Count number system with digits from 0 to 20 is seen later to pass to one using digits 0 to 19, which leads us to propose that even earlier there may have been an initial zeroless bijective numeration system whose digits ran from 1 to 20.
    [Show full text]
  • Report Association for Computing Machinery
    June 1954 REPORT TO THE ASSOCIATION FOR COMPUTING MACHINERY FIRST GLOSSARY of PROGRAMMING TERMINOLOGY Committee on Nomenclature 'Co Wo Adams R. FoOsborn J 0 W 0 Backus G. W. Patterson J 0 W. Carr, III J. Svigals J. Wegstein Grace Murray Hopper, Chairman COPIES Copies of this glossary are available at 25, each. When ordered by mail, the price is 50~for the first copy and 25<'f for each 'additional copy sent to one address. Please address all orders, with cash or -check enclosed" to the Association for Computing Machinery" 2 East 63rd Street, New York 2'1" N.Y. ACKNOWLEDQ]lJIENT This (·programmer's glossary" had its ,inception in a glos­ sary compiled by Dr. Grace Murray Hopper for the Workshops on AutomaticOoding held in 1953 under the sponsorship of the Bur­ eau of Oensus, the Office of the Air Comptroller, and Remington Rand" Inc. '!he answers to the plea for criticisms and sugges­ tions made in that first version were most generous o Everyef­ fort has been made to include all of them or to arbitrate fairly those in conflict. Both versions have borrowed heavi~y from the "St1mdards on Electronic Computers: l)efinitionsof' Terms" 1950"" Proceedipgs of the I.R.E." Vol. 39 No.3" pp. 271-277" March 1951" and from the "Glossary", Computers and Automation~ Vol. 2" Nos. 2" 4 and 9" March" May, and December" 1953. The commit­ tee extends its thanks to the authors ,of those glossaries and to the many others who have contributed their time and thoughts to the preparation of this glossary.
    [Show full text]
  • Parallel Branch-And-Bound Revisited for Solving Permutation Combinatorial Optimization Problems on Multi-Core Processors and Coprocessors Rudi Leroy
    Parallel Branch-and-Bound revisited for solving permutation combinatorial optimization problems on multi-core processors and coprocessors Rudi Leroy To cite this version: Rudi Leroy. Parallel Branch-and-Bound revisited for solving permutation combinatorial optimization problems on multi-core processors and coprocessors. Distributed, Parallel, and Cluster Computing [cs.DC]. Université Lille 1, 2015. English. tel-01248563 HAL Id: tel-01248563 https://hal.inria.fr/tel-01248563 Submitted on 27 Dec 2015 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Ecole Doctorale Sciences Pour l’Ingénieur Université Lille 1 Nord-de-France Centre de Recherche en Informatique, Signal et Automatique de Lille (UMR CNRS 9189) Centre de Recherche INRIA Lille Nord Europe Maison de la Simulation Thèse présentée pour obtenir le grade de docteur Discipline : Informatique Parallel Branch-and-Bound revisited for solving permutation combinatorial optimization problems on multi-core processors and coprocessors. Défendue par : Rudi Leroy Novembre 2012 - Novembre 2015 Devant le jury
    [Show full text]
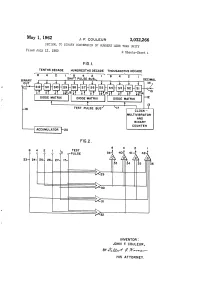
  • Is Hirihiti?H DECIMAL
    May 1, 1962 J. F. COULEUR 3,032,266 DECIMAL TO BINARY CONVERSION OF NUMBERS LESS THAN UNITY Filed July 12, l960 2 Sheets-Sheet l FG.I. TENTHS DECADE HUNDREDTHS DECADE THOUSANDTHS DECADE 4. 2 is hirihiti?h DECIMAL TERAF DODE MATRIX DODE MATRIX DODE MATRIX TEST PULSE BUS CLOCK - MULTIVBRATOR AND BNARY COUNTER ACCUMULATOR NVENTOR: JOHN F. COULEUR, BY (4-f (? W2----- HIS AT TORNEY. May 1, 1962 J. F. COULEUR 3,032,266 DECIMAL TO BINARY CONVERSION OF NUMBERS LESS THAN UNITY Filed July 12, 1960 2. Sheets-Sheet 2 F.G.3. BINARY BINARY CODED DECMAL TENTHS HUNDREDTHS THOUSANDTHS Row 3 2 8 NUMBER O O OOO OOO () OO OOO O T (2) O O O O O OO S (3) O OO OOO OO T (4) O OO OOO OOO S (5) O OO OOO OOO T (6) OO O O OOO OOO S (7) OO OO OOO OOO T (8) OO OOO OO O OOO S (9) OO OOO OOO O T (O) OOO OOO OO OO S (I) OOO OOO OO OO T (2) OOOO OO OO OOO S (3) OOOO OO OO OOO T (4) OOOO OO OOO OO O S (5) OOOO OO O OOO. T (6) OOOO OO OO OOO S (7) OOOO OO OO O T (8) OOOO OO OO O O S (9) OOOO OO OO OO T (20) OOOO OOO O OO O S (2) T MEANS TEST AND ADD THREE TO ANY DECADE 2 5 S MEANS SHIFT FIG.4. BINARY BNARY CODED DECMA -------------------IO- IO-2 IO-3 IO-4 10-5 O-6 (3) (2) (8) () (2) (5) OO OOO OOO OOO OOO OO OO OOO O OOO OOO OOO T O O O Oi Oi O O OOO O.
    [Show full text]
  • Design and Architecture of New 11:2 Decimal Compressors
    Sådhanå (2019) 44:125 Ó Indian Academy of Sciences https://doi.org/10.1007/s12046-019-1110-4Sadhana(0123456789().,-volV)FT3](0123456789().,-volV) Design and architecture of new 11:2 decimal compressors PRABIR SAHA* and PUJA SAMANTA National Institute of Technology Meghalaya, Shillong, India e-mail: [email protected]; [email protected] MS received 5 January 2018; revised 11 March 2019; accepted 19 March 2019; published online 25 April 2019 Abstract. Design and architectures of new 11:2 decimal compressors have been reported in this paper. Two design methodologies viz. delay and area optimized compressors have been introduced and implemented through tree structure of decimal number system. The architectures have been realized through vertical carry save addition algorithm, wherein to build up such addition of unconventional (4221 and 5211) binary coded decimal technique has been incorporated. Configurations of such compressors have been prototyped and tran- sistor level implementation have been carried out to evaluate performance parameters like speed (propagation delay), power dissipation, area and area delay product. The architecture has been validated by Cadence virtuoso platform using 90 nm, 65 nm and 45 nm CMOS technology which provides useful statistics to determine the compressor’s performance parameters. The propagation delay of the delay optimized compressor equals to *0.094 ns while the propagation delay of the area optimized compressor is *0.124 ns using 90 nm CMOS technology at 1 V supply voltage. The reported architectures are *24% and *41% faster from its counterpart. Keywords. Cadence; decimal compressor; layout area; power consumption; propagation delay. 1. Introduction multiplication; hence it reduces the overall delay of the multiplication.
    [Show full text]