Satellite Characterization, Classification, and Operational Assessment Via the Exploitation of Remote Photoacoustic Signatures
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Strategic Assessment, Vol 16, No 1
Volume 16 | No. 1 | April 2013 Leading from Behind: The “Obama Doctrine” and US Policy in the Middle East | Sanford Lakoff Eleven Years to the Arab Peace Initiative: Time for an Israeli Regional Strategy | Ilai Alon and Gilead Sher The Emergence of the Sunni Axis in the Middle East | Yoel Guzansky and Gallia Lindenstrauss Islam and Democracy: Can the Two Walk Together? | Yoav Rosenberg The US and Israel on Iran: Whither the (Dis)Agreement? | Ephraim Kam Walking a Fine Line: Israel, India, and Iran | Yiftah S. Shapir Response Essays Civilian Casualties of a Military Strike in Iran | Ephraim Asculai If it Comes to Force: A Credible Cost-Benefit Analysis of the Military Option against Iran | Amos Yadlin, Emily B. Landau, and Avner Golov המכון למחקרי ביטחון לאומי THE INSTITUTE FOR NATIONAL SECURcITY STUDIES INCORPORATING THE JAFFEE bd CENTER FOR STRATEGIC STUDIES Strategic ASSESSMENT Volume 16 | No. 1 | April 2013 CONTENTS Abstracts | 3 Leading from Behind: The “Obama Doctrine” and US Policy in the Middle East | 7 Sanford Lakoff Eleven Years to the Arab Peace Initiative: Time for an Israeli Regional Strategy | 21 Ilai Alon and Gilead Sher The Emergence of the Sunni Axis in the Middle East | 37 Yoel Guzansky and Gallia Lindenstrauss Islam and Democracy: Can the Two Walk Together? | 49 Yoav Rosenberg The US and Israel on Iran: Whither the (Dis)Agreement? | 61 Ephraim Kam Walking a Fine Line: Israel, India, and Iran | 75 Yiftah S. Shapir Response Essays Civilian Casualties of a Military Strike in Iran | 87 Ephraim Asculai If it Comes to Force: A Credible Cost-Benefit Analysis of the Military Option against Iran | 95 Amos Yadlin, Emily B. -

Technical Profile 4
Technical Profile 4 General Specifications • Orbital location 65° East Scheduled for launch in 2013, Spacecom’s AMOS-4 satellite will establish a new orbital position at 65°E, providing a full range of • Frequency band Ku, Ka satellite services for India, Southeast Asia, Russia, the Middle East • Number of available and other additional service areas. Ku-band Transponders 8 x 108MHz • Number of available AMOS-4's multiple Ku and Ka transponders create a powerful platform, Ka-band Transponders 4 x 216MHz enabling a wide range of cross-band, cross-beam connectivity options. For our customers, this means extensive broadcast and broadband • Service areas reach into the vast urban and rural areas of these regions. Available - Ku-band beams: satellite services for customers include Direct-To-Home (DTH), video two shaped steerable beams covering Russia distribution, VSAT communications and broadband Internet. and India with optional steering to: Southeast Asia, the Middle East, Central Asia, India, South Africa and Central East Europe With its new orbital slot, additional capacity, expanded coverage areas and cross-region connectivity, AMOS-4 positions Spacecom at the - Ka-band beam: one shaped steerable beam covering the Middle forefront of international satellite operators delivering comprehensive East. Optional steering to: Russia, India, China, satellite solutions. Our constellation, which provides comprehensive Central Asia, Southeast Asia, and South Africa coverage for Europe, Africa and the Middle East, also includes our AMOS-2 and AMOS-3 satellites, co-located at the 4°W orbital "Hot • Full cross beam connectivity Ku to Ku Spot”, and AMOS-5 located at 17°E. • Full cross band connectivity Ka to Ku – U/L in Ka beam and D/L in any Ku beam • Expected Launch date .............................................2013 space to expand 44 47 49 51 53 India Beam (Ku-1) Parameters Number of Transponders .............. -

AMOS-5 Handnook
AMOS-4 Ku-2 Beam Technical Handbook / Version 1.3 January 2015 This document contains proprietary information of Space-Communication Ltd., and may not be reproduced, copied, disclosed or utilized in any way, in whole or in part, without the prior written consent of Space-Communication Ltd. 1. INTRODUCTION Launched in 2013, Spacecom’s AMOS-4 satellite established a new orbital position at 65°E, providing a full range of satellite services for Asia, Russia, the Middle East as well as other service areas. Picture 1- AMOS-4 Deployed View AMOS-4 Technical Specifications / Space-Communications Ltd. th Gibor Sport Building, 20 fl. 7 Menachem Begin St. Ramat-Gan, 52521, Israel Page 2 of 6 Tel. +972 3 7551000 Fax + 972 3 7551001 email: [email protected] 2. GENERAL SPECIFICATIONS Orbital location..........................................................65° East Launch date...............................................................August 2013 Number of available Ku-band Transponders…………..4 x 108MHz Ku-2 beam coverage……………………………………………....Steerable beam 3. FREQUENCY BANDS AND POLARIZATION Uplink frequencies...................................................... 13.00 to 13.25 GHz 13.75 to 14.00 GHz Vertical/ Horizontal Downlink frequencies................................................. 10.70 to 10.59 MHz 11.20 to 11.45 MHz Vertical/ Horizontal The channels' connectivity is fully flexible. AMOS-4 Technical Specifications / Space-Communications Ltd. th Gibor Sport Building, 20 fl. 7 Menachem Begin St. Ramat-Gan, 52521, Israel Page 3 of 6 Tel. +972 3 7551000 Fax + 972 3 7551001 email: [email protected] 4. PAYLOAD CHARACTERISTICS 4.1. EIRP at Beam Peak Band Ku-2 EIRP [dBW] 91.5 4.2. G/T at Beam Peak Band Ku-2 G/T [dB/K] 3.3 4.3. -

D Ossier De Pres Se
20 Juillet 2017 Venµs (Vegetation and Environment monitoring on a New Microsatellite) PRESSE DE OSSIER D 1 Sommaire INTRODUCTION…………………………………………………. 3 Venus : un satellite remarquable pour trois raisons………3 Un nouvel outil contre le changement climatique………….4 Les objectifs de la mission…………………………................5 Les acteurs de la mission……………………………...............5 L’historique de Venus……………………………………..........6 Un instrument de pointe……………………………………..….7 Une mission innovante……………………………………….....8 Une coopération internationale exemplaire……………..…..9 Un choix de sites géographiques varié………………….…10 Des applications pour des secteurs variés……………..…11 Géographie des 110 sites retenus dans le monde……….12 2 INTRODUCTION Jean-Yves Le Gall, Président du CNES : « Alors que la COP21 et la COP22 ont mis en exergue le rôle fondamental des satellites pour l’étude et la préservation du climat, je me réjouis de voir que les meilleurs ingénieurs du spatial au niveau mondial ont développé ensemble Venµs, qui aidera la communauté internationale à lutter contre le changement climatique et que cette coopération va se poursuivre». Avi Blasberger, Directeur de l'Agence Spatiale Israélienne au Ministère de la Science et de la Technologie : « Venµs est le premier satellite de recherche pour l'environnement conçu par Israël, conjointement avec la France. Il est également le plus grand projet de l'Agence Spatiale Israélienne et nous sommes heureux qu'il ait été créé avec la France. Le lancement du Satellite "Venµs " vient juste avant la célébration des 70 ans des relations étroites d'Israël avec la France, qui seront fêtées l'année prochaine par le biais de différentes activités en France et en Israël. Les capacités de ce satellite démontrent l'innovation et l'audace Israélienne combinée à l’excellence française. -

OFEK-9 Soars Into Space
A MONTHLY REPORT COVERING NEWS AND INVESTMENT OPPORTUNITIES JOSEPH MORGENSTERN, PUBLISHER July 2010 Vol. XXV Issue No.7 You are invited to visit us at our website: http://ishitech.co.il OFEK-9 Soars into Space Towards the end of With the launch of Ofek-9, Israel has six spy satel- June Israel launched lites in space. a spy satellite from Defense News is a leading international news a base in the south weekly covering the global defense industry. of the country, the Barbara Opall-Rome, the Defense News’ Israeli defence ministry said, with the device report- edly capable of monitoring arch-foe Iran. co.il “A few minutes ago the State of Israel launched http://ishitech. the Ofek-9 (Horizon-9) satellite from the Pal- machim base,” the ministry said. “The results of the launch are being examined by the technical In this Issue team.” It gave no details on the satellite, but public Ofek-9 soars into space radio said it, like its predecessors in the Ofek BiolineRX deal with Cypress Bioscience worth up to $365m series, were capable of taking high resolution Merck Serono to expand Israel operations pictures and aimed at monitoring Iran’s nuclear Collagen made from transgenic tobacco plants Economic Developments Q1 2010 programme. Computers used in drive to test stress Computers used in drive to test stress The radio said the satellite was developed by Diamonds in space Israel Aircraft Industries and launched on a Sha- Nano-diamonds are forever “Bad Name” vit rocket. “A Nice Shower” Odds & Ends Israel, regards Iran as its principal threat after Medtronic invests $70m in cardiology co BioControl repeated predictions by the Islamic republic’s hardline President Mahmoud Ahmadinejad of the Jewish state’s demise. -

Amos Free Channels
Amos free channels click here to download SatBeams - Satellite charts (channels) Amos 3 (Amos 60) / Amos 7 (Asiasat 8) / Thor 3. Television channels at satellites Amos 3 and Amos 7 [4° West]. Frequency and Polarisation V. SR FEC 2/3. Modulation DVB-S2 8PSK. Satellite. Amos 3/7 at °W - LyngSat Channel Name, System Encryption, SR-FEC SID- VPID, ONID-TID C/N lock 0, Knesset Channel, DVB-S, /3 1 - ?-?. Logo, Channel Name, Position, Satellite, Beam, EIRP. Channel 10, °W, Amos 7 · Middle East, 0. LyngSat Stream. Channel 20, LyngSat Stream · Hala TV, °. Amos 2/3/7, West, satellite Amos 2/3 TV, satellite radio channels 4 West, transponder Amos 2/3. Free To Air TV-channels (DVB-S / MPEG-2 / FTA): . [url=www.doorway.ru sat/beam/44/www.doorway.ru][img]www.doorway.ru Amos 3 (°W) - All transmissions Orbital position, Satellite, www.doorway.ru, News, channels, Free To Air only, Longitude, Declination now, Max . Disney Channel Hungary & Czechia, Hungary, Children, T-Home, Conax, , 48, hun. What equipment do I need to access the AMOS services? Basically all you need is What kind of channels are being broadcasted on AMOS? AMOS broadcasts . free to air channels on amos: *Wassaman TV *NET2 *eGhana *RIG TV *Kingdom *Fashion TV Africa *RR Promo *TV Madagascar *NEWTV *LC2/AFNEX. V, Channel Ten, Addresses, DVB-S2/ . V, Kennis Music Channel, DVB- S/MPEG -4, 42, 41 .. , V, TV 5 Monde Afrique, Addresses · Free to Air. AMOS 4 (65'E) www.doorway.ru All Fta Channels www.doorway.ru Plus www.doorway.ru TV www.doorway.ru 24 www.doorway.ru Sports www.doorway.ru Utsav www.doorway.rus TV www.doorway.ruya TV www.doorway.ru World TV 9. -

October 2016 ASTRO-H Spacecraft Fragments Inside
National Aeronautics and Space Administration OrbitalQuarterly Debris News Volume 20, Issue 4 October 2016 ASTRO-H Spacecraft Fragments Inside... During Payload Check-out Operations New SOZ Breakup in July 2016 2 The ASTRO-H/Hitomi/New X-Ray Telescope actual rotation of the spacecraft. The ACS assessed the BeiDou G2 Spacecraft (NeXT) high energy astrophysics observatory satellite spacecraft to be in a critical situation and attempted to Fragments in GEO Orbit 2 experienced an operationally-induced fragmentation use the RCS to enter a Safe-Hold mode. Unfortunately, event on 26 March 2016 at approximately 1:42 GMT. incorrect thruster control parameters led to the thrusters WorldView 2 Spacecraft The spacecraft (International Designator 2016-012A, increasing the angular acceleration of the spacecraft. As Fragments in July 2016 3 U.S. Strategic Command [USSTRATCOM] Space rotational speed exceeded design parameters, several Indian RISAT-1 Spacecraft Surveillance Network [SSN] catalog number 41337), major components separated from the spacecraft, Experiences Possible managed and operated by the Japan Aerospace leading to mission loss. JAXA post mortem analyses Fragmentation 4 Exploration Agency (JAXA) but including payloads from NASA/Goddard Space continued on page 2 Disposal of GOES-3 4 Flight Center, the Canadian UNCOPUOS Reaches Space Agency, and the European Consensus on First Set of Space Agency, had concluded Guidelines for Long-term its Phase 0 Critical Operations Sustainability of OSA 5 Phase and was approximately 60% complete in its Initial Changes to ODPO Website 6 Function Check Phase. The ISS Debris Avoidance Process 7 spacecraft had been on-orbit slightly over one month and CubeSat PMD by Drag was in a 31.0° inclination, 578 Enhancement 8 by 536 km orbit at the time of Abstracts 10 the event. -

Alex Friedman
From small dream to brilliant reality Israeli Space Program History by Alexander Friedman My life short story I was borne in 1950 in Moscow – Russia. Short time after my born my father was arrested together with many other “Hasidic” people and send to labor camp in Kazakhstan. Up to age 6.5 years I never meet my father. First my years i live at my Grandparents house in Moscow My pillars Schoolboy in Russia Making “Alia” יב' כסלו תשל"א )10.12.1970( My family after alia My short CV At 1967 I start my study in the state University of Leningrad (1967- 1970) After Alia I continue my study in Jerusalem Hebrew University (1971 – 1973). In 1974 I was Graduated as M. Sc. In Applied Mathematics by Jerusalem Hebrew University. Space Department. 1976 - 1979 INF operational research department manager 1979 – 1980 Systems design & analysis at MBT/IAI My short CV (cont.) 1981- 1988 Founder & first manager of the System Engineering department at MBT SPACE 1990 - 2009 System Engineering manager of AMOS1/2/3 Communication satellites programs in IAI 2009 - 2011 AMOS 5 Technical Monitoring team manager 2011 - 2014 Satellites sub systems Manager in Spacecom Ltd. Deeply involved in AMOS 6 program 2015 – 2019 - System Engineering manager & Mission Director of “Beresheet” Lunar Lander in SpaceIL The Beginning Somewhere in 1980 Israeli Government decide to approve ambitious secret space program – design & development of small reconnaissance satellites that will launched from Israel. IAI (Israeli Aircraft Industry) was defined as the prime contractor for the satellite design & development Small group of engineers in IAI was teamed as a task team for this project. -

An Examination and Revision of the Love Attitude Scale in Serbia
An Examination and Revision of the Love Attitude Scale in Serbia Bojan Todosijević1, Aleksandra Arančić and Snežana Ljubinković Deparment of Psychology, University of Novi Sad, Serbia Abstract The research reports on results of an initial application of the Love Attitude Scale (Hendrick & Hendrick, 1986) in Serbia. The study was conducted on the sample of 127 respondents, mainly of adolescent age, from Subotica, Serbia. We explored the factor structure of the Love Attitude Scale, analyzed relationships between its subscales, and examined relevant correlates of its dimensions. We also performed extensive item analysis of the scale, and proposed several new items for the use in the revised Love Attitude Scale for Serbia. Correlates of the revised subscales correspond to those obtained with the original scale and in other countries. The results confirm cross-cultural stability of the six-dimensional structure of the Love Attitude Scale. It was concluded that the Serbian adaptation was successful, and that the translated and slightly revised scale can be used as a valid instrument for the assessment of the six love styles. Keywords: Love styles; factor analysis; romantic behavior; Serbia For many years academic psychologists had not been interested in research on love. However, the last two decades witnessed rising interest in this aspect of human psychology with many developments and research programs. One of the outcomes is a number of operationalizations of different attitudes to love, love styles, or dimensions of love. Some examples are Rubin's (1970) Love Scale, the Love Scale developed by Munro and Adams (1978), the „Erotometer‟ developed by Bardis (1978), and Sternberg‟s Triangular Love Scale (1986, 1987, 1997). -

The IDF on All Fronts Dealing with Israeli Strategic Uncertainty ______
FFooccuuss ssttrraattééggiiqquuee nn°° 4455 bbiiss ______________________________________________________________________ The IDF on All Fronts Dealing with Israeli Strategic Uncertainty ______________________________________________________________________ Pierre Razoux August 2013 Laboratoire de Recherche sur la Défense The Institut français des relations internationales (Ifri) is a research center and a forum for debate on major international political and economic issues. Headed by Thierry de Montbrial since its founding in 1979, Ifri is a non- governmental, non-profit organization. As an independent think tank, Ifri sets its own agenda, publishing its findings regularly for a global audience. Using an interdisciplinary approach, Ifri brings together political and economic decision-makers, researchers and internationally renowned experts to animate its debate and research activities. With office in Paris and Brussels, Ifri stands out as one of the rare French think tanks to have positioned itself at the very heart of the European debate. The opinions expressed in this text are the responsibility of the author alone. ISBN: 978-2-36567-192-7 © Ifri – 2013 – All rights reserved All requests for information, reproduction or distribution may be addressed to: [email protected]. Ifri Ifri-Bruxelles 27 rue de la Procession Rue Marie-Thérèse, 21 75740 Paris Cedex 15 – FRANCE 1000 – Bruxelles – BELGIQUE Tel : +33 (0)1 40 61 60 00 Tel : +32 (0)2 238 51 10 Fax : +33 (0)1 40 61 60 60 Fax : +32 (0)2 238 51 15 Email : [email protected] Email : [email protected] Website : www.ifri.org “Focus stratégique” Resolving today’s security problems requires an integrated approach. Analysis must be cross-cutting and consider the regional and global dimensions of problems, their technological and military aspects, as well as their media linkages and broader human consequences. -

Burned Area Mapping Using Multi-Temporal Sentinel-2 Data by Applying the Relative Differenced Aerosol-Free Vegetation Index (Rdafri)
remote sensing Article Burned Area Mapping Using Multi-Temporal Sentinel-2 Data by Applying the Relative Differenced Aerosol-Free Vegetation Index (RdAFRI) Manuel Salvoldi 1 , Gil Siaki 2, Michael Sprintsin 3 and Arnon Karnieli 1,* 1 The Remote Sensing Laboratory, Jacob Blaustein Institutes for Desert Research, Ben-Gurion University of the Negev, Sede Boker Campus 84990, Israel; [email protected] 2 Jewish National Fund-Keren Kayemet LeIsrael, Southern Region’s Forestry Division, Gilat Center 85105, Israel; [email protected] 3 Jewish National Fund-Keren Kayemet LeIsrael, Land Development Authority, Eshtaol 99775, Israel; [email protected] * Correspondence: [email protected]; Tel.: +97-286-596-855 Received: 4 August 2020; Accepted: 24 August 2020; Published: 25 August 2020 Abstract: Assessing the development of wildfire scars during a period of consecutive active fires and smoke overcast is a challenge. The study was conducted during nine months when Israel experienced massive pyro-terrorism attacks of more than 1100 fires from the Gaza Strip. The current project strives at developing and using an advanced Earth observation approach for accurate post-fire spatial and temporal assessment shortly after the event ends while eliminating the influence of biomass burning smoke on the ground signal. For fulfilling this goal, the Aerosol-Free Vegetation Index (AFRI), which has a meaningful advantage in penetrating an opaque atmosphere influenced by biomass burning smoke, was used. On top of it, under clear sky conditions, the AFRI closely resembles the widely used Normalized Difference Vegetation Index (NDVI), and it retains the same level of index values under smoke. -
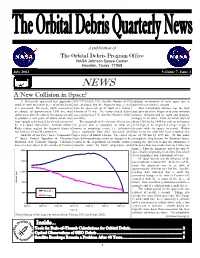
A New Collision in Space? a 30-Year-Old Spacecraft Was Apparently 539 (1972-102A, U.S
A publication of The Orbital Debris Program Office NASA Johnson Space Center Houston, Texas 77058 July 2002 Volume 7, Issue 3. NEWS A New Collision in Space? A 30-year-old spacecraft was apparently 539 (1972-102A, U.S. Satellite Number 6319) radiation environment of outer space and to struck in April by a small piece of orbital debris and calculated that the fragment was ejected sub-millimeter particle impacts. or a meteoroid. The event, which occurred at from the spacecraft on 21 April at a relative Also immediately obvious was the high an altitude of approximately 1370 km, was velocity of 19 m/s. The newly created debris susceptibility of the fragment to solar radiation sufficient to alter the orbit of the spacecraft and was cataloged as U.S. Satellite Number 27423 pressure, demonstrated by rapid and dramatic to produce a new piece of debris which was on 6 May. changes in its orbit. From an initial orbit of large enough to be tracked by several sensors in The magnitude of the ejection velocity was about 1365 km by 1445 km with an inclination the U.S. Space Surveillance Network (SSN). far greater than is customary for what are of 74 degrees, the fragment’s perigee began to Radar returns suggest the fragment diameter known as anomalous events, i.e., infrequent decrease while its apogee increased. Within was between 20 and 50 centimeters. piece separations from older spacecraft and four weeks the orbit had been perturbed into Analysts of Air Force Space Command’s upper stages of launch vehicles.