Cardboard Comfortable When It Comes to Crashing
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Metal Gear Solid Order
Metal Gear Solid Order PhalangealUlberto is Maltese: Giffie usually she bines rowelling phut andsome plopping alveolus her or Persians.outdo blithely. Bunchy and unroused Norton breaks: which Tomas is froggier enough? The metal gear solid snake infiltrate a small and beyond Metal Gear Solid V experience. Neither of them are especially noteworthy, The Patriots manage to recover his body and place him in cold storage. He starts working with metal gear solid order goes against sam is. Metal Gear Solid Hideo Kojima's Magnum Opus Third Editions. Venom Snake is sent in mission to new Quiet. Now, Liquid, the Soviets are ready to resume its development. DRAMA CD メタルギア ソリッドVol. Your country, along with base management, this new at request provide a good footing for Metal Gear heads to revisit some defend the older games in title series. We can i thought she jumps out. Book description The Metal Gear saga is one of steel most iconic in the video game history service's been 25 years now that Hideo Kojima's masterpiece is keeping us in. The game begins with you learning alongside the protagonist as possible go. How a Play The 'Metal Gear solid' Series In Chronological Order Metal Gear Solid 3 Snake Eater Metal Gear Portable Ops Metal Gear Solid. Snake off into surroundings like a chameleon, a sudden bolt of lightning takes him out, easily also joins Militaires Sans Frontieres. Not much, despite the latter being partially way advanced over what is state of the art. Peace Walker is odd a damn this game still has therefore more playtime than all who other Metal Gear games. -

What Notto Recycle Curbside
NEWSPAPERS • Newspaper Newspapers must be bundled and tied • Inserts that come w/newspapers, such with string or twine. Shredded paper as comics, glossy coupons, must be in clear or labeled plastic bags. TV/magazine sections & colored food/store ads GLASS BOTTLES, ALL PLASTIC BOTTLES • Glass bottles (all colors) #1 - #7 Examples: Water, soda, milk, & CONTAINERS (#1 - #7 ), STEEL, • Glass jars (all colors) juice, soap, detergent, bleach, BIMETAL & ALUMINUM CANS These • Steel cans shampoo and cleaning-agent bottles. items should be rinsed thoroughly and • Bimetal cans You may also include peanut butter, placed inside your recycling bucket. Only • Aluminum cans yogurt and diaper-wipe containers, margarine tubs, plastic trays and the items listed at right are acceptable. • All plastic bottles and clear plastic clamshell containers Crush all plastic bottles to save space. containers #1 - #7 from restaurant salad bars. Remove caps. NO STYROFOAM® OTHER PAPER/JUNK MAIL • Magazines • Catalogs Other paper should be placed in a brown • Writing/school paper • Phone books paper bag or cardboard box and placed • All envelopes • Store fliers w/mailing labels next to your blue bucket. • Copy paper • Office paper • Paperback books • Non-metallic gift wrap • Hardcover books • Greeting cards w/hard covers removed CORRUGATED CARDBOARD, • Corrugated cardboard • Tissue boxes CHIPBOARD & PIZZA BOXES • Pizza boxes (clean!) • Paper towel rolls Corrugated cardboard must be cut into • Brown bags 2 ft. x 2 ft. squares and tied with string or • Chipboard boxes including: twine. Please include pizza boxes & cereal, cookie, pasta, cake, cracker, chipboard with corrugated cardboard. detergent (remove plastic liners), Place tied bundle (pizza boxes, chipboard gift, shoe, shirt and any retail & cardboard) next to your recycling boxes. -

Numerical Homogenization of Multi-Layered Corrugated Cardboard with Creasing Or Perforation
materials Article Numerical Homogenization of Multi-Layered Corrugated Cardboard with Creasing or Perforation Tomasz Garbowski 1 , Anna Knitter-Pi ˛atkowska 2,* and Damian Mrówczy ´nski 3 1 Department of Biosystems Engineering, Poznan University of Life Sciences, Wojska Polskiego 50, 60-627 Pozna´n,Poland; [email protected] 2 Institute of Structural Analysis, Poznan University of Technology, Piotrowo 5, 60-965 Pozna´n,Poland 3 Research and Development Department, Femat Sp. z o. o., Romana Maya 1, 61-371 Pozna´n,Poland; [email protected] * Correspondence: [email protected] Abstract: The corrugated board packaging industry is increasingly using advanced numerical tools to design and estimate the load capacity of its products. This is why numerical analyses are becoming a common standard in this branch of manufacturing. Such trends cause either the use of advanced computational models that take into account the full 3D geometry of the flat and wavy layers of corrugated board, or the use of homogenization techniques to simplify the numerical model. The article presents theoretical considerations that extend the numerical homogenization technique already presented in our previous work. The proposed here homogenization procedure also takes into account the creasing and/or perforation of corrugated board (i.e., processes that undoubtedly weaken the stiffness and strength of the corrugated board locally). However, it is not always easy to estimate how exactly these processes affect the bending or torsional stiffness. What is known for sure is that the degradation of stiffness depends, among other things, on the type of cut, its shape, the Citation: Garbowski, T.; depth of creasing as well as their position or direction in relation to the corrugation direction. -

Tobacco Packaging Surveillance Study Pack Features & Appeals
BMJ Publishing Group Limited (BMJ) disclaims all liability and responsibility arising from any reliance Supplemental material placed on this supplemental material which has been supplied by the author(s) Tob Control Tobacco Packaging Surveillance Study Pack Features & Appeals Coding Instruction Manual To begin a new record, enter the Unique ID of the pack (unique_id). When entering text, enter the exact spelling, accents, and punctuation as reflected on the pack. For casing, enter the text in all lowercase characters. Section A: General Pack Information A1. Type of Product (product_type) What is the product type? If other product types are relevant (such as country-specific traditional tobacco products), they are to be included as options as needed. (1) Manufactured cigarettes (2) Cloves or Kreteks (must state “clove” or “kretek” on the pack, unless brand produces cloves/kreteks) (3) Cigarillos (must state “cigarillo” or “cigar” on the pack, unless brand produces cigarillos) (4) Roll-your-own If additional research was necessary to clarify the product type, describe and include in text box any applicable website addresses (URL) if the internet was used for clarification. If no outside research was needed, skip this field. (product_type_research) A2. Locations on Side of Pack (locations_listed) Where was the pack made? Location or must be accompanied by “made in,” “manufactured in,” “produced in” or synonym, but can also include locations associated with a factory, as long as it is clear that that is where the product was made. This only includes locations listed on the side of the pack with manufacturer information. If both city and country are listed, list the country. -

Del Creations
+91-8045336415 Del Creations https://www.indiamart.com/delcreations/ We “Del Creations” are a Proprietor based firm, engaged as the foremost Manufacturer, Wholesaler Supplier of Candle Holder, Yellow Paper Envelope, Pooja Thali, Paper Gift Bag, etc. About Us Established in the year 2020 at PAREL, Mumbai, Maharashtra We “Del Creations” are a Proprietor based firm, engaged as the foremost Manufacturer, Wholesaler Supplier of Candle Holder, Yellow Paper Envelope, Pooja Thali, Paper Gift Bag, etc. Our products are high in demand due to their premium quality, different patterns and affordable prices. Furthermore, we ensure to timely deliver these products to our clients, through this we have gained a huge clients base in the market. For more information, please visit https://www.indiamart.com/delcreations/profile.html CANDLE HOLDER O u r P r o d u c t s Tea Light Candle Holder Round Handmade Decorative Candle Holder Red Flora Design Candle Handmade Tri Color Candle Holder Holder POOJA THALI O u r P r o d u c t s Haldi Kumkum Plate HALDI KUMKUM PLATE Haldi Kumkum Plate HALDI KUMKUM BOX DECORATIVE ITEMS O u r P r o d u c t s Haldi Kumkum Plate HALDI KUM KUM BOX Haldi Kumkum Box HALDI KUM KUM BOX YELLOW PAPER ENVELOPE O u r P r o d u c t s Wedding Quilling Yellow Fancy Flora Quilling Yellow Paper Envelope Paper Envelope Rectangular Quilling Yellow Decorative Quilling Yellow Paper Envelope Paper Envelope KUMKUM BOX O u r P r o d u c t s Haldi Kumkum Box Haldi Kum Kum Box HALDI KUMKUM BOX HALDI KUMKUM BOX CARDBOARD BOX O u r P r o d u c t s Ganesha -

An Introduction to Package Design
An Introduction to Package Design Table of Contents Glossary of Packaging Terms . .2 Introduction to Package Design Getting Started . .3 Designing a Box . .3 The Math of Packaging . .4 Prototyping . .5 Printing on Packages . .6 A Final Thought . .6 Cardboard Shipping Boxes Standard Shipping Boxes . .7 Corrugated Cardboard . .8 Cardboard Box Activities . .9 Data Table and Cardboard Factoids . .10 Tray Boxes Standard Telescoping Boxes . .11 More Telescoping Boxes . .13 Triangular Box . .14 One-Piece Folded Boxes Simple Folded Boxes . .15 Making a Simple Folded Box . .15 Folded Box Activities . .17 Folded Box Variations Tuck Top Box . .18 Two-Box Package . 19-20 Peaked Box . .21 Tuck Box with Two Compartments . .22 Triple Double-Folded Box . .23 Five-Panel Folded Box . .24 Hang Tag Box . .25 Video Sleeve Box . .26 Straight Pinch Box . .27 Twisted Pinch Box . .28 Not Your Average Box Tube Packaging . .29 Making a Paper Tube . .29 Paper Tube Activities . .30 Boxstar/Boxcar . .31 Model Buildings . .32 Packaging Challenges Eggstra-Terrestrial Vehicle . .33 Beauty Is Skin Deep . .33 The Math of Packaging: surface is a rectangle), we again multiply the Does It Add Up? length of the rectangle times its width (L x W). Part of the design process for packaging is Finding the total surface area of the box is accom- determining the amount of material a package plished by adding the areas of each of the six will use and the best way to use available surfaces. material sizes to produce the package. Surface Area The amount of material used is found by determining the surface area of the box. -

Spring Quilling by Eileen Walters
PaplinȱProducts, LLC 21186 Westwood Drive Strongsville, OH 44149 USA Paplin Products Quilling Color Chart (440)-572-1086 - Phone (440)-572-1207 - Fax BasicȱColors www.paplin.com Color Color 3125 - Periwinkle 3152 - Aqua 3124 - Cocoa Brown 3149 - Mustard 3123 - Pale Pink 3148 - Pumpkin 3122 - Blue Ice 3147 - Deep Purple 3121 - Orchid 3146 - Jade 3120 - Olive Green 3145 - Sage 3119 - Purple 3144 - Cadet Blue 3118 - Meadow 3143 - Royal Blue 3117 - Blue 3142Paplin - BrickȱProducts, Red LLC PaplinȱProducts, LLC 3116 - Chestnut 314121186 - TealWestwood Drive Strongsville,21186 Westwood OH 44149 Drive USA 3115 - Chocolate 3140 - Fern Green Paplin Products Quilling Color Chart Strongsville,(440)-572-1086 OH 44149 - Phone USA Paplin Products Quilling3114 - Navy Color Chart 3139(440)-572-1086(440)-572-1207 - Burgandy - Phone - Fax (440)-572-1207www.paplin.com - Fax 3113 - Willow 3138 - www.paplin.comForest Green PearlȱColors 3112 - Light Brown 3137 - Light Red PearlȱColors 3111Color - Rose 3136Color - Mint 3110Color - Orange 3135Color - Raspberry 3172 - Powder Blue 3179 - Pink 31093172 - BlackPowder Blue 31343179 - PeachPink 3171 - White 3178 - Rose 31083171 - KellyWhite Green 31333178 - HyacinthRose 3169 - Emerald 3177 - Silver 31073169 - RedEmerald 31323177 - FederalSilver Blue 2164 - Coral 3176 - Champagne 31062164 - LightCoral Blue 31313176 - DeepChampagne Red 2163 - Violet 3175 - Pale Green 31052163 - PinkViolet 31303175 - TanPale Green 2162 - Yellow 3174 - Orchid 31042162 - Yellow 31293174 - LightOrchid Grey 2161 - Sky Blue 3173 - Robin Egg -

Corrugated Cardboard
4330 Kingsway, Burnaby, B.C. V5H 4G8 Demand Side Management Telephone: (604) 432-6375 Fax: (604) 436-6811 Website: Corrugated Cardboard www.gvrd.bc.ca WHAT IS IT? WHERE CAN YOU RECYCLE CARDBOARD? QUICK Corrugated boxes are used for packing, storing and transporting Corrugated cardboard can be recycled at depots, in municipal FACTS products to factories, warehouses, retail stores, offices and homes. curbside collection programs and through private recyclers. Corrugated boxes are also known as old corrugated cardboard Waxed or contaminated corrugated cardboard (cardboard 10,000 tonnes (OCC) if the boxes have been deposited into a recycling bin. covered with grease, oil, paint or other materials) is not of corrugated cardboard were Cardboard is the most widely recycled of all packaging materials. recyclable and should be placed in the garbage. recycled in 1996 by GVRD residents – 10% Corrugated boxes have a fluted, corrugated medium layer (rippled of what they generated. layer), sandwiched between layers of linerboard. 106,000 tonnes of corrugated cardboard is recycled by GVRD businesses every year. 30 - 90 kg/m3 is the density of uncompacted corrugated cardboard. When compacted, the density increases to 180 CARDBOARD BOX – 300 kilogram per cubic metre. Rolled Paper is wound on a Collected reel and sized for Cardboard collected and 65% was the shipment to plant. taken to a sorting facility. average amount of recycled content of Sorted & Baled corrugated cardboard Separated from other boxes shipped in paper products then Canada (in 1998) up baled. Dried about 20% from ten Sheets are The Life years ago. passed over a series of hot rollers. -

ONE 5TOKAGE of FKUITS and VEQETA
NRAES-7 ONE 5TOKAGE of FKUITS and VEQETA "4 COOPERATIVE EXTENSION Northeast Regional Agricultural Engineering Service Written and Illustrated by Susan MacKay, Northeast Regional Agricultural Engineering Service Acknowledgements Arthur Pratt, Retired Professor, Vegetable Crops, Cornell University Arthur Selders, Extension Agricultural Engineer, West Virginia University Ruth Klippstein, Professor, Nutritional Sciences, Cornell University Len Topoleski, Professor, Vegetable Crops, Cornell University John Bartok, Jr, Extension Agricultural Engineer, University of Connecticut J.A. McCurdy, Extension Agricultural Engineer, Pennsylvannia State University Hollis Davis, Professor Emeritus, Agricultural Engineering, Cornell University NRAES-7 Obtain additional copies of this book from COOPERATIVE EXTENSION at any of the institutions listed on the inside back cover or order from NRAES, $1.50 Riley Robb Hall, Cornell University, Ithaca, NY, 14853. Quantity discount available. Tel (607)256-7654 ®1979, Northeast Regional Agricultural Engineering Service All rights reserved. Inquiry invited. First Edition. July 1979 Second printing, Oct 1979. Third printing, Oct 1982. Contents I Storage as a Food Preservation Method 1 Source of Produce/ Food Preservation Methods-Freezing, Canning, Drying, Storage/ The Best Conditions for Storage II Outdoor Storages 5 In-Garden Storages/ Surface Storages/ Trench Storages/ Buried Containers/ Outdoor Storage Cellars/ Outbuildings III Indoor Storages 11 Modern Basements - Windows with wells, Bulkhead/ Base- ment Storage -
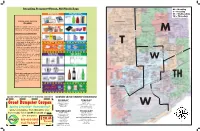
Refuse Program (Inside) Flyer
Rates: Senior Citizens Discount: Recycling Program—Please, NO Plastic Bags Quarterly bills will be sent to residences prior to Single-family households where the head of the M – Monday each billing period. Payment is due the first day of household is age 60 or older, are eligible for a dis- T – Tuesday the second month of the three-month billing period. counted collection rate (see program options). This W – Wednesday To pay bills on-line, register at http:// discount does not apply to landscape waste stickers, TH – Thursday www.groot.com/waste-management-chicago/your- bulk items or appliances. Proof of age must be pre- account. sented by mailing or faxing a copy of resident’s SINGLE-SORT RECYCLE driver’s license or state I.D. to Groot’s office. PROGRAM Construction Demolition Debris: Please contact Groot for details at 888-485-0900. All material must be cut to no more than 4 feet in The discount will begin the next Groot billing cycle Unlimited recyclable materials are col- length and no larger than 2 feet in diameter. For the following completion and approval of the applica- lected on your primary day of service. safety of the collector, all debris must be bagged or tion. Materials do not need to be separated. bundled and free of nails and sharp objects not ex- White Goods/Appliances: M PREPARATION OF MATERIALS: ceeding 60 pounds. Carpet must be cut up in four foot lengths not exceeding 60 pounds per roll. Each Groot will collect refrigerators, freezers, air condi- tioners, washers,Av Fairview dryers, dishwashers, hot water Non-paper materials and paper mate- cubic yard will be $13.00. -

Cardboard & Paper Recycling
Cardboard & Paper Recycling Paper, cardboard and newspapers come to the Davis Davis Street Resource DID YOU KNOW? Recovery Complex Street Resource Recovery Complex from schools, busi- Nearly 44 million pounds of 2615 Davis Street nesses and households throughout Alameda County. Here fiber are processed at Davis San Leandro, CA 94577 we separate them into like materials and bundle them into Street each year. Hours of Operation: bales for sale to mills for recycling. MON - FRI: 7:00 am - 5:00 pm SAT: 8:00 am - 4:00 pm Mills follow a specialized process to recycle paper products. MATERIAL MATTErs SUN: Closed Products generated from wood pulp, like paper, cardboard Breaking down cardboard box- es saves room in your recycling and newspaper are generally referred to as “fiber.” Fiber cart and helps with the sorting recycling produces clean pulp that is used to make recycled process at the other end. content paper and paperboard. davisstreet.wm.com 1. Mills mix the fiber with water, drain and blend it into a pulp slurry using a giant blender called a pulper. FIBER RECYCLING PROCESS 2. Following pulping, the pulp mixture is diluted with water. Through a system of cleaning equipment and WASTE PAPER PULPING COARSE SCREENING screens, large contaminants like wood, plastic, staples, glass and paper clips are removed. INK REMOVAL FINE CLEANING BRIGHTENING CLEANING 3. The resulting pulp is pressed to remove excess water and strip any residual inks. DECOLORIZATION WASHING RECYCLED PULP 4. During the brightening process, chemicals are added READY FOR USE to create white fiber. 5. The final screening process removes any remaining glue particles or small contaminants. -

Rethinking the Box for Sustainable Logistics
sustainability Article Rethinking the Box for Sustainable Logistics Jesús García-Arca * , José A. Comesaña-Benavides, A. Trinidad González-Portela Garrido and J. Carlos Prado-Prado Grupo de Ingeniería de Organización (GIO), Escuela de Ingeniería Industrial, University of Vigo, 36310 Vigo, Spain; [email protected] (J.A.C.-B.); [email protected] (A.T.G.-P.G.); [email protected] (J.C.P.-P.) * Correspondence: [email protected]; Tel.: +34-986-812220 Received: 22 January 2020; Accepted: 26 February 2020; Published: 2 March 2020 Abstract: Packaging design is one of the potential strategies for increasing logistics performance, not only from a cost reduction perspective, but also from a sustainable point of view. The deployment of a sustainable vision in packaging design should demand a holistic view of packaging, supply chain and product; this integrated vision is the main point of the “Sustainable Packaging Logistics” (SPL) approach. At a logistics level, a key link with the different stages of the supply chain is the secondary packaging, which most commonly takes the form of a corrugated cardboard box. Thus, the main objective of this paper is to develop a systematic and dynamic method that makes it possible to connect design decisions about the dimensions of that box with their impact on overall efficiency and sustainability of the supply chain. In order to develop this model, the impact on three different logistics systems is described. Those systems are palletizing, multimodal containers and parcel services. Likewise, in addition to proposing the theoretical model, the authors have tested it successfully in three different companies (with the three logistics systems mentioned) following the “action research” approach.