DOCSLIB.ORG

The Higgs Boson and Electroweak Symmetry Breaking

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

The Higgs Boson and Electroweak Symmetry Breaking 2. Models of EWSB M. E. Peskin SLAC Summer Institute, 2004 In the previous lecture, I discussed the simplest model of EWSB, the Minimal Standard Model. This model turned out to be a little too simple. It could describe EWSB, but it cold not explain its physical origin. In this lecture, I would like to discuss three models that have been put forward to explain the physics of EWSB: • Technicolor • Supersymmetry • Little Higgs I hope this will give you an idea of the variety of possiblities for the next scale in elementary particle physics. Technicolor: ϕ was introduced by Higgs in analogy to the theory of superconductivity. There, Landau and Ginzburg had introduced ϕ as a phenomenological charged quantum fluid. Their equations account for the Meissner effect, quantized flux tubes, critical fields and Type I-Type II transitions, ... Bardeen, Cooper, and Schrieffer showed that pairs of electrons near the Fermi surface can form bound states that condense into the macroscopic wavefunction ϕ at low temperatures. This suggests that we should build the Higgs field as a composite of some strongly interacting fermions that form bound states. Weinberg, Susskind: QCD has strong interactions, and also fermion pair condensation. For 2 flavors i i i i L = qLγ · DqL + qRγ · DqR has the global symmetry SU(2)xSU(2)xU(1). If quarks have strong interactions, scalar combinations of q and q should condense into a macroscopic wavefunction in the vacuum state: j i = ∆ = 0 !qLqR" δij ! Act with global symmetries. We find a manifold of vacuum states j i = ∆ !qLqR" Vij In any given state, SU(2)xSU(2)xU(1) is spontaneously broken to SU(2)xU(1). The degrees of freedom of V(x) are Goldstone bosons: a a V = eiπ σ /fπ a Identify π with the 3 pi mesons. m2 m2 Nambu and Jona-Lasinio: this is why π ! ρ The pions would be massless-exact Goldstones, if mu = md = 0 f π is the pion decay constant = 93 MeV µ5a b µ ab !0| J !π " = ip fπδ ! Now couple this system to SU(2)xU(1) gauge bosons 1 1 1 qL ( , Y ) uR (0, Y + ) dR (0, Y − ) 2 2 2 Only the gauge symmetry 3 3 iα(I +Y ) iα(I +Y ) qL → e qL qR → e qR is conserved. So, Q + I3+Y must correspond to a massless gauge boson. The 3 other generators must correspond to massive gauge bosons. The symmetry breaking occurs precisely because the W boson has a purely left-handed coupling. To compute the masses explicitly, write a a σ ! ! 1 DµV = ∂µV − igW V − ig BY V + ig BV (Y ± ) 1 2 2 L = 2 tr † µ 4fπ DµV D V for !V " = 1 " 2 1 2 g + + g − − g 3 3 g 3 = fπ tr W σ + W σ + W σ Bσ L 4 !√ √ 2 − 2 ! ! 2 2 ! 2 fπ ! − 1 " ! = g2W! +W + (gW 3 g B)2 ! (1) 4 " 2 − # This is the same structure as the MSM, where we found g2 g2 + g!2 m2 = v2 m2 = v2 W 4 Z 4 To obtain the correct masses, we need a scaled-up QCD - “technicolor” - in which v mT ρ ∼ mρ · ∼ 2 TeV fπ The analogue of the Higgs boson in this theory is the σ or a0 ++ 0 resonance of QCD. In technicolor, this appears as a peak (better, a shoulder) in S-wave WW and ZZ scattering at ~ 1600 GeV. ! A much better signal is the T ρ , which appears as a resonance in P-wave WW scattering and in e+e− → W +W − This resonance is already strongly constrained by LEP 2 data. 4.5 4 ALEPH 3.5 R 3 /M 2.5 R ' 2 1.5 1 excluded 0.5 95% CL 0 0 200 400 600 800 1000 1200 1400 1600 1800 MR (GeV) There are more serious phenomenological problems with technicolor. Mixing of the T ρ with W, Z alters the precision electroweak 2 predictions at the 2-3% level, increasing s in θ w and m W above the MSM expectation. Corrections of order 3% are also expected in Γ(Z → bb) Fermion masses are generated by higher-dimension operators 1 i Q q q uj M 2 L R L R There is no simple mechanism for flavor conservation, so we 0 0 expect large corrections to K , B mixing, b → sγ Fixes for these problems may exist if the strong-coupling theory has special properties (“walking technicolor”, “conformal fixed point”). Supersymmetry: Supersymmetry (SUSY) is a symmetry that relates bosons and fermions with the same SU(2)xU(1) quantum numbers. This is a very deep theoretical idea which will be explained at the school next week. You will hear then about a number of phenomenological advantages of supersymmetry as a theory of the next energy scale. SUSY is particularly interesting for the problem of EWSB because it gives a rationale and a restrictive theoretical framework for introducing elementary scalar fields. In this discussion, only a few aspects of SUSY will be important: • Every boson or fermion in the theory has a partner, with spin differing by 1/2 • Coupling constants in the renormalizable interactions of the partners are equal to the corresponding Standard Model parameters • SUSY must be spontaneously broken; this is parameterized by “soft” SU(2)xU(1)-invariant mass terms. • Quadratic divergences in boson mass terms cancel between loop diagrams with bosons and fermions ~ h h + ~ h The Higgs boson sector of SUSY is unexpectedly complex. 1 Y = ± There must be two Higgs doublet fields with 2 including only one gives an anomalous gauge theory SU(2) SU(2) U(1) + U(1) ~ ~h h1 2 SU(2) SU(2) quark-Higgs couplings are only of the form L = − ij − ij λd dRH1α"αβQβ λu uRH2α"αβQβ so it is still true that all flavor violation can be moved into the CKM matrix. (But, soft SUSY-breaking terms may provide new sources of flavor violation.) H 1 , H 2 have 8 degrees of freedom ➤ 0 0 ❨3 eaten Goldstones) + (CP even h , H ) − + (CP odd A 0 ) + ( H + , H ) The Higgs mass terms come from soft SUSY breaking: 2 2 2 2 L = −MH1|H1| − MH2|H2| These parameters do not have huge additive corrections, but they do evolve - on a log scale - due to RG effects. For example, the coupling to SU(2) gauginos gives w~ d 2 3 2 MH2 = − αwm(w!) − · · · d log Q 2π ~ H h2 2 A more important effect is the coupling to top quarks. ~ tL H2 t 2 R This sends M H 2 to negative values as Q decreases. 2 2 The same effect applies to M !t L , M !t R These fields compete with the Higgs field to go unstable. SUSY thus raises a new question about EWSB. SUSY rationalizes the elementary scalar field, but in the process it introduces many elementary scalars. Any one can obtain a vacuum expectation value. If ! H 2 " #= 0 , we break SU(2)xU(1). If ! t R # != 0 , we break color SU(3) but preserve SU(2). " Which behavior is predicted ? Assume that all soft scalar masses are equal at a very high mass scale; integrate the RG equations down: Here are the relevant RG equations. Notice that the Higgs boson is favored, both by color/SU(2) factors and by the influence of the gluino: 2 d 2 λt 2 2 2 2 8 2 M = + · 1 · (M + M + MH2 + At ) − αsm(g!) − · · · d log Q !tL (4π)2 !tL !tR 3π 2 d 2 λt 2 2 2 2 8 2 M = + · 2 · (M + M + MH2 + At ) − αsm(g!) − · · · d log Q !tR (4π)2 !tL !tR 3π 2 d 2 λt 2 2 2 2 MH2 = + · 3 · (M + M + MH2 + At ) (1) d log Q (4π)2 !tL !tR If the Higgs coupling to the top quark is the largest coupling in the theory, this effect is likely to dominate and drive EWSB. Little Higgs: Return to the idea that the Higgs boson is a composite of strongly-interacting fermions. The problems we met with this idea can be ameliorated by raising the strong- interaction scale. Then we can implement a different strategy (Kaplan-Georgi). Let the strong-interaction symmetry breaking preserve SU(2)xU(1). Let the multiplet of Goldstone bosons include the Higgs doublet ϕ . Then, by coupling to gauge fields or to new particles, break down the constraints that keep ϕ exactly massless. Here is a simple realization: Arkani-Hamed, Cohen, Katz, Nelson Consider a gauge theory with the symmetry SU(3)xSU(3)xU(1), broken by strong interactions to SU(3)xU(1). This gives an SU(3) octet of Goldstone bosons a a a a Φ H V = e2iΠ t /f 2iΠ t = ! −H† φ " in which the H is a doublet. We will want f ∼ 1 TeV , Mρ ∼ 10 TeV All fields in Π must be massless if the SU(3) symmetries † V → ΛRV ΛL are respected. Coupling this structure to the top quarks. We need to put top quarks into the representations u χL = b UR uR U L with an extra singlet quark. The Lagrangian is L = −λ1f ( 0 0 uR ) V χL − λ2fU RUL † The first term has the symmetry V → V ΛL χ → ΛLχ The second term has the symmetry V → ΛRV Either symmetry suffices to insure that H is exactly massless. Thus, to build a Higgs potential, we need to involve both interaction terms.
Recommended publications
  • Spacetime Geometry from Graviton Condensation: a New Perspective on Black Holes

    Spacetime Geometry from Graviton Condensation: a New Perspective on Black Holes

    Spacetime Geometry from Graviton Condensation: A new Perspective on Black Holes Sophia Zielinski née Müller München 2015 Spacetime Geometry from Graviton Condensation: A new Perspective on Black Holes Sophia Zielinski née Müller Dissertation an der Fakultät für Physik der Ludwig–Maximilians–Universität München vorgelegt von Sophia Zielinski geb. Müller aus Stuttgart München, den 18. Dezember 2015 Erstgutachter: Prof. Dr. Stefan Hofmann Zweitgutachter: Prof. Dr. Georgi Dvali Tag der mündlichen Prüfung: 13. April 2016 Contents Zusammenfassung ix Abstract xi Introduction 1 Naturalness problems . .1 The hierarchy problem . .1 The strong CP problem . .2 The cosmological constant problem . .3 Problems of gravity ... .3 ... in the UV . .4 ... in the IR and in general . .5 Outline . .7 I The classical description of spacetime geometry 9 1 The problem of singularities 11 1.1 Singularities in GR vs. other gauge theories . 11 1.2 Defining spacetime singularities . 12 1.3 On the singularity theorems . 13 1.3.1 Energy conditions and the Raychaudhuri equation . 13 1.3.2 Causality conditions . 15 1.3.3 Initial and boundary conditions . 16 1.3.4 Outlining the proof of the Hawking-Penrose theorem . 16 1.3.5 Discussion on the Hawking-Penrose theorem . 17 1.4 Limitations of singularity forecasts . 17 2 Towards a quantum theoretical probing of classical black holes 19 2.1 Defining quantum mechanical singularities . 19 2.1.1 Checking for quantum mechanical singularities in an example spacetime . 21 2.2 Extending the singularity analysis to quantum field theory . 22 2.2.1 Schrödinger representation of quantum field theory . 23 2.2.2 Quantum field probes of black hole singularities .
  • SLAC-PUB3031 January 1983 (T) SPONTANEOUS CP VIOLATION IN

    SLAC-PUB3031 January 1983 (T) SPONTANEOUS CP VIOLATION IN

    SLAC-PUB3031 January 1983 (T) - . SPONTANEOUS CP VIOLATION IN EXTENDED TECHNICOLOR MODELS WITH HORIZONTAL V(2)t @ U(~)R FLAVOR SYMMETRIES (II)* WILLIAM GOLDSTEIN Stanford Linear Accelerator Center Stanford University, Stanford, California S&l05 ABSTRACT -- The results presented in Part I of this paper are extended to-include previously neglected electro-weak degrees of freedom, and are illustrated in a toy model. A problem associated with colored technifermions is identified and discussed. Some hope is offered for the disappointing quark mass matrix obtained in Part I. Submitted to Nuclear Physics B * Work supported by the Department of Energy, contract DEAC03-76SF00515. 1. INTRODUCTION In a previous paper [l], hereafter referred to as I, we investigated sponta- neous CP violation in a class of extended technicolor (ETC) models [2,3,4,5]. We constructed the effective Hamiltonian generated by broken EZ’C interactions and minimized its contribution to the vacuum energy, as called for by Dashen’s - . Theorem [S]. As originally pointed out by Dashen, and more recently by Eichten, Lane and Preskill in the context of the EK’ program, this aligning of the chiral vacuum and Hamiltonian can lead to CP violation from an initially CP symmet- ric theory [7,8]. The ETC models analyzed in I were distinguished by the global flavor invari- ance of the color-technicolor forces: GF = n u(2)L @ u@)R (1) For-- these models, we found that, in general, the occurrence of spontaneous CP violation is tied to CP nonconservation in the strong interactions and, thus, - to an unacceptably large neutron electric dipole moment.
  • Composite Higgs Sketch

    Composite Higgs Sketch

    Composite Higgs Sketch Brando Bellazzinia; b, Csaba Cs´akic, Jay Hubiszd, Javi Serrac, John Terninge a Dipartimento di Fisica, Universit`adi Padova and INFN, Sezione di Padova, Via Marzolo 8, I-35131 Padova, Italy b SISSA, Via Bonomea 265, I-34136 Trieste, Italy c Department of Physics, LEPP, Cornell University, Ithaca, NY 14853 d Department of Physics, Syracuse University, Syracuse, NY 13244 e Department of Physics, University of California, Davis, CA 95616 [email protected], [email protected], [email protected], [email protected], [email protected] Abstract The couplings of a composite Higgs to the standard model fields can deviate substantially from the standard model values. In this case perturbative unitarity might break down before the scale of compositeness, Λ, is reached, which would suggest that additional composites should lie well below Λ. In this paper we account for the presence of an additional spin 1 custodial triplet ρ±;0. We examine the implications of requiring perturbative unitarity up to the scale Λ and find that one has to be close to saturating certain unitarity sum rules involving the Higgs and ρ couplings. Given these restrictions on the parameter space we investigate the main phenomenological consequences of the ρ's. We find that they can substantially enhance the h ! γγ rate at the LHC even with a reduced Higgs coupling to gauge bosons. The main existing LHC bounds arise from di-boson searches, especially in the experimentally clean channel ρ± ! W ±Z ! 3l + ν. We find that a large range of interesting parameter arXiv:1205.4032v4 [hep-ph] 30 Aug 2013 space with 700 GeV .
  • Technicolor Evolution Elizabeth H

    Technicolor Evolution Elizabeth H

    Technicolor Evolution Elizabeth H. Simmons∗ Physics Department, Boston University† This talk describes how modern theories of dynamical electroweak symmetry breaking have evolved from the original minimal QCD-like technicolor model in response to three key challenges: Rb, flavor-changing neutral currents, and weak isospin violation. 1. Introduction In order to understand the origin of mass, we must find both the cause of electroweak symme- try breaking, through which the W and Z bosons obtain mass, and the cause of flavor symmetry breaking, by which the quarks and leptons obtain their diverse masses and mixings. The Standard Higgs Model of particle physics, based on the gauge group SU(3)c × SU(2)W × U(1)Y accommo- dates both symmetry breakings by including a fundamental weak doublet of scalar (“Higgs”) + 2 = φ = † − 1 2 bosons φ φ0 with potential function V (φ) λ φ φ 2 v . However the Standard Model does not explain the dynamics responsible for the generation of mass. Furthermore, the scalar sector suffers from two serious problems. The scalar mass is unnaturally sensitive to the pres- ence of physics at any higher scale Λ (e.g. the Planck scale), as shown in fig. 1. This is known as the gauge hierarchy problem. In addition, if the scalar must provide a good description of physics up to arbitrarily high scale (i.e., be fundamental), the scalar’s self-coupling (λ) is driven to zero at finite energy scales as indicated in fig. 1. That is, the scalar field theory is free (or “trivial”). Then the scalar cannot fill its intended role: if λ = 0, the electroweak symmetry is not spontaneously broken.
  • Investigation of Theories Beyond the Standard Model

    Investigation of Theories Beyond the Standard Model

    Investigation of Theories beyond the Standard Model Sajid Ali1, Georg Bergner2, Henning Gerber1, Pietro Giudice1, Istvan´ Montvay3, Gernot Munster¨ 1, Stefano Piemonte4, and Philipp Scior1 1 Institut fur¨ Theoretische Physik, Universitat¨ Munster,¨ Wilhelm-Klemm-Str. 9, D-48149 Munster¨ E-mail: fsajid.ali, h.gerber, p.giudice, munsteg, [email protected] 2 Theoretisch-Physikalisches Institut, Universitat¨ Jena, Max-Wien-Platz 1, D-07743 Jena E-mail: [email protected] 3 Deutsches Elektronen-Synchrotron DESY, Notkestr. 85, D-22603 Hamburg E-mail: [email protected] 4 Fakultat¨ fur¨ Physik, Universitat¨ Regensburg, Universitatsstr.¨ 31, D-93053 Regensburg E-mail: [email protected] The fundamental constituents of matter and the forces between them are splendidly described by the Standard Model of elementary particle physics. Despite its great success, it will be superseded by more comprehensive theories that are able to include phenomena, which are not covered by the Standard Model. Among the attempts in this direction are supersymmetry and Technicolor models. We report about our non-perturbative investigations of the characteristic properties of such models by numerical simulations on high-performance computers. 1 Introduction The physics of elementary particles has a marvellous theoretical framework available, which is called the Standard Model. It accurately describes a vast number of phenom- ena and experiments. In the Standard Model the fundamental interactions among parti- cles are described in terms of gauge field theories, which are characterized by an infinite- dimensional group of symmetries. Despite its great success it is evident that the Standard Model does not offer a complete description of the fundamental constituents of matter and their interactions.
  • Little Higgs Model Limits from LHC Arxiv:1307.5010V2 [Hep-Ph] 5 Sep

    Little Higgs Model Limits from LHC Arxiv:1307.5010V2 [Hep-Ph] 5 Sep

    DESY 13-114 Little Higgs Model Limits from LHC Input for Snowmass 2013 Jurgen¨ Reuter1a, Marco Tonini2a, Maikel de Vries3a aDESY Theory Group, D{22603 Hamburg, Germany ABSTRACT The status of several prominent model implementations of the Little Higgs paradigm, the Littlest Higgs with and without discrete T-parity as well as the Simplest Little Higgs are reviewed. For this, we are taking into account a fit of 21 electroweak precision observables from LEP, SLC, Tevatron together with the full 25 fb−1 of Higgs data reported by ATLAS and CMS. For the Littlest Higgs with T-parity an outlook on corresponding direct searches at the 8 TeV LHC is included. We compare their competitiveness with the EW and Higgs data in terms of their exclusion potential. This contribution to the Snowmass procedure contains preliminary results of [1] and serves as a guideline for which regions in parameter space of Little Higgs models are still compatible for the upcoming LHC runs and future experiments at arXiv:1307.5010v2 [hep-ph] 5 Sep 2013 the energy frontier. For this purpose we propose two different benchmark scenarios for the Littlest Higgs with T-parity, one with heavy mirror quarks, one with light ones. [email protected] [email protected] [email protected] 1 Introduction: the Little Higgs Paradigm The first run of LHC at 2 TeV, 7 TeV, and 8 TeV centre of mass energies has brought as main results the discovery of a particle compatible with the properties of the Standard Model (SM) Higgs boson as well as with electroweak precision tests (EWPT), and no significant excesses that could be traced to new particles or forces.
  • Collider Signals of Bosonic Technicolor

    Collider Signals of Bosonic Technicolor

    W&M ScholarWorks Undergraduate Honors Theses Theses, Dissertations, & Master Projects 2013 Collider Signals of Bosonic Technicolor Jennifer Hays College of William and Mary Follow this and additional works at: https://scholarworks.wm.edu/honorstheses Part of the Physics Commons Recommended Citation Hays, Jennifer, "Collider Signals of Bosonic Technicolor" (2013). Undergraduate Honors Theses. Paper 625. https://scholarworks.wm.edu/honorstheses/625 This Honors Thesis is brought to you for free and open access by the Theses, Dissertations, & Master Projects at W&M ScholarWorks. It has been accepted for inclusion in Undergraduate Honors Theses by an authorized administrator of W&M ScholarWorks. For more information, please contact [email protected]. Abstract We propose a model of Electroweak Symmetry Breaking (EWSB) that includes a technicolor sector and a Higgs-like boson. The model includes a bound state of technifermions held together 0 by a new strong interaction, denoted πTC , which decays like a Standard Model (SM) higgs boson. By observing an excess in diphoton final states, the ATLAS and CMS collaborations have recently discovered a Higgs-like boson at 125 GeV. For m 0 < 200 GeV, we determine πTC bounds on our model from the Large Hadron Collider (LHC) search for new scalar bosons 0 decaying to γγ. For m 0 > 200 GeV, we consider the dominant decay mode πTC ! Zσ, πTC where σ is a scalar boson of the model. An excess in this channel could provide evidence of the new pseudoscalar. i Contents 1 Introduction 1 1.1 The Need for Electroweak Symmetry Breaking . .1 1.2 Technicolor Models . .2 1.3 Bosonic Technicolor .
  • Minimal Walking Technicolor: Phenomenology and Lattice Studies

    Minimal Walking Technicolor: Phenomenology and Lattice Studies

    Minimal Walking Technicolor: Phenomenology and Lattice Studies Kimmo Tuominen Department of Physics, University of Jyv¨askyl¨a, Finland Helsinki Institute of Physics, University of Helsinki, Finland 1 Introduction and a concrete model During recent years there has been lot of theoretical effort dedicated to understand the dynamics of (quasi)conformal gauge theories, i.e. theories in which the evolution of the coupling towards the infrared is governed by a (quasi)stable fixed point. Along these lines, important recent progress towards the understanding of the phase diagram of strongly coupled gauge theories as a function of the number of flavors, colors and matter representations was made in [1, 2]. These results, then, allowed one to uncover new walking technicolor theories where the walking behavior arises with minimal matter content and also led to concrete models of the unparticle concept [3] in terms of the underlying strong dynamics [4]. Particularly simple candidates for walking technicolor were identified in [1] as the ones with Nf = 2 either in the adjoint representation of SU(2) or in the sextet representation of SU(3). In this presentation we concentrate in detail on the first of the above mentioned two cases, i.e. the minimal walking technicolor (MWTC). As a specific technicolor model, this model resolves the naturality, hierarchy and triviality problems of the Standard Model (SM) in the usual way. Due to the proposed walking dynamics, if embedded within an extended technicolor (ETC) framework [5], this model allows one to suppress flavor changing neutral currents (FCNC) down to the observed level yet generating phenomenologically feasible quark mass spectrum.
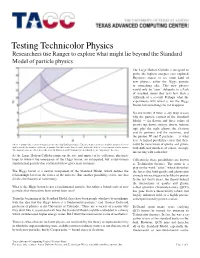
  • Testing Technicolor Physics

    Testing Technicolor Physics

    Testing Technicolor Physics Researchers use Ranger to explore what might lie beyond the Standard Model of particle physics The Large Hadron Collider is designed to probe the highest energies ever explored. Physicists expect to see some kind of new physics, either the Higgs particle or something else. This new physics would only be “seen” obliquely in a flash of smashed atoms that lasts less than a trillionth of a second. Perhaps what the experiments will reveal is not the Higgs Boson, but something else yet to appear. No one knows if there is any deep reason why the particle content of the Standard Model — six flavors and three colors of quarks (up, down, strange, charm, bottom, top), plus the eight gluons, the electron and its partners and the neutrinos, and the photon, W and Z particles — is what it is. A logical possibility exists that there Above is a map of the technicolor particles theories that DeGrand studies. The axes represent (horizontal) the number of colors could be more kinds of quarks and gluons, and (vertical) the number of flavors of quarks. The different colors describe different kinds of color structure for the quarks. with different numbers of colors, strongly The shaded bands are where these theorists (D. Dietrich and F. Sannino) predict that there are “unparticle” theories. interacting with each other. As the Large Hadron Collider ramps up the rate and impact of its collisions, physicists hope to witness the emergence of the Higgs boson, an anticipated, but as-yet-unseen Collectively, these possibilities are known fundamental particle that scientists believe gives mass to matter.
  • The Standard Model and Strings

    The Standard Model and Strings

    Future/present Experiments The Standard Model and Strings - Can They Be Connected? High energy colliders: the primary tool • 1 The standard model NMSSM – TEVThe AstandaTROrdN;mFoermildel ab, 1.96 TeV pp¯ , exploration nMSSM • • UMSSM 2 |N | in UMSSM – Large Hadron Collider (LHC); CERN, 14 TeV pp, high lum16 inosity, TesTtiesngtingthethestandastandard rmod modeldel 0.8 • • discovery (Discovery machine for ) supersymmetry, Rp violation, string 1 0 remnants (e.g., Z!, exotics, Higgs); o! r compositeness, dynamical symmetry ProblemProblems s • • breaking, Higgless theories, Little Higgs,0.6 large extra dimensions, ) · · · Bey– InternationalBeyondondthethestandastandaLirdnerdamor moColdedelliderl (ILC), in planning; • • + (Singlino in 0.4 2 500 GeV-1 TeV e e−, cold technol| ogy, high precision studies 15 Where(PreciNewaTsionreeVwpaephrametergoing?ysics suggess to maptedback to|N string scale) • • by string constructions 0.2 CP violation (B decays, electric dipole moments), CKM universality, • flavoWherer changingare we neutrgoing?al currents (e.g0., µ eγ, µN eN, B φK ), • 0 → 100 → 200 → 300s M 0 (GeV) B violation (proton decay, n n¯ oscillations), neutrin!o physics − 1 Chicago (12/1/2005) Paul Langacker (FNAL/Penn/IAS) Chicago (12/1/2005) Paul Langacker (FNAL/Penn/IAS) Chicago (12/1/2005) Paul Langacker (FNAL/Penn/IAS) Future/present Experiments The New Standard Model High energy colliders: the primary tool • Standard model, supplemented with neutrino mass (Dirac or • – TEVMajoATranROa)N;: Fermilab, 1.96 TeV pp¯ , exploration – Large HadronSUC(3)olliderSU(L(2)HCU);(1)CERNclas,
  • Preliminary Draft Introduction to Supersymmetry and Supergravity

    Preliminary Draft Introduction to Supersymmetry and Supergravity

    Preliminary draft Introduction to Supersymmetry and Supergravity Jan Louis Fachbereich Physik der Universit¨atHamburg, Luruper Chaussee 149, 22761 Hamburg, Germany ABSTRACT These lecture give a basic introduction to supersymmetry and supergravity. Lectures given at the University of Hamburg, winter term 2013/14 January 23, 2014 Contents 1 The Lorentz Group and the Supersymmetry Algebra 4 1.1 Introduction . .4 1.2 The Lorentz Group . .4 1.3 The Poincare group . .5 1.4 Representations of the Poincare Group . .5 1.5 Supersymmetry Algebra . .7 2 Representations of N = 1 Supersymmetry and the Chiral Multiplet 8 2.1 Representation of the Supersymmetry Algebra . .8 2.2 The chiral multiplet in QFTs . 10 3 Super Yang-Mills Theories 13 3.1 The massless vector multiplet . 13 3.2 Coupling to matter . 13 3.3 Mass sum rules and the supertrace . 14 4 Superspace and the Chiral Multiplet 17 4.1 Basic set-up . 17 4.2 Chiral Multiplet . 18 4.3 Berezin integration . 19 4.4 R-symmetry . 20 5 The Vector Multiplet in Superspace and non-Renormalization Theorems 21 5.1 The Vector Multiplet in Superspace . 21 5.2 Quantization and non-Renormalization Theorems . 22 6 The supersymmetric Standard Model 24 6.1 The Spectrum . 24 6.2 The Lagrangian . 25 7 Spontaneous Supersymmetry Breaking 26 7.1 Order parameters of supersymmetry breaking . 26 7.2 Goldstone's theorem for supersymmetry . 26 7.3 Models for spontaneous supersymmetry breaking . 27 7.3.1 F-term breaking . 27 1 7.3.2 D-term breaking . 28 8 Soft Supersymmetry Breaking 30 8.1 Excursion: The Hierarchy and Naturalness Problem .
  • Sangam@HRI March 25-30, 2013 Tao Han (PITT PACC) Pittsburgh

    Sangam@HRI March 25-30, 2013 Tao Han (PITT PACC) Pittsburgh

    Higgsology: ! Theory and Practice" Tao Han (PITT PACC) PITTsburgh Particle physics, Sangam@HRI Astrophysics and Cosmology Center March 25-30, 2013 1 Pheno 2013: May 6-8" 2 It is one of the most " exciting times:" 10000 - Selected diphoton sample Data 2011+2012 8000 Sig+Bkg Fit (m =126.8 GeV) H Bkg (4th order polynomial) 6000 ATLAS Preliminary Events / 2 GeV H"!! CMS Preliminary s = 7 TeV, L = 5.1 fb-1 ; s = 8 TeV, L = 19.6 fb-1 4000 35 s = 7 TeV, Ldt = 4.8 fb-1 Data 2000 # s = 8 TeV, #Ldt = 20.7 fb-1 30 Z+X * g 500 Z! ,ZZ 400 25 300 m =126 GeV 200 H Events / 3 GeV 100 0 20 -100 -200 100 110 120 130 140 15015 160 Events - Fitted bk m!! [GeV] 10 5 0 80 100 120 140 160 180 Tao Han 3 m4l [GeV] m = 125.5 GeV ATLAS Preliminary H W,Z H ! bb s = 7 TeV: %Ldt = 4.7 fb-1 s = 8 TeV: %Ldt = 13 fb-1 H ! $$ s = 7 TeV: %Ldt = 4.6 fb-1 s = 8 TeV: %Ldt = 13 fb-1 (*) H ! WW ! l#l# s = 7 TeV: %Ldt = 4.6 fb-1 s = 8 TeV: %Ldt = 20.7 fb-1 H ! "" s = 7 TeV: %Ldt = 4.8 fb-1 s = 8 TeV: %Ldt = 20.7 fb-1 (*) H ! ZZ ! 4l s = 7 TeV: %Ldt = 4.6 fb-1 s = 8 TeV: %Ldt = 20.7 fb-1 Combined ! = 1.30 " 0.20 s = 7 TeV: %Ldt = 4.6 - 4.8 fb-1 s = 8 TeV: %Ldt = 13 - 20.7 fb-1 -1 0 +1 Signal strength (!) 4 Fabiola Gianotti, ALTAS spokesperson Runner-up of 2012 Person of the year 9/30/13 This discovery opens up a new era in HEP! In these Lectures, I wish to convey to you: • This is truly an “LHC Revolution”, ever since the “November Revolution” in 1974 for the J/ψ discovery! • It strongly argues for new physics beyond the Standard Model (BSM).