MASSES of EXOPLANETS from ASTROMETRY. G. Fritz Benedict And, Barbara E
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Towards a Demonstrator for Autonomous Object Detection on Board Gaia Shan Mignot
Towards a demonstrator for autonomous object detection on board Gaia Shan Mignot To cite this version: Shan Mignot. Towards a demonstrator for autonomous object detection on board Gaia. Signal and Image processing. Observatoire de Paris, 2008. English. tel-00340279v2 HAL Id: tel-00340279 https://tel.archives-ouvertes.fr/tel-00340279v2 Submitted on 21 Nov 2008 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. OBSERVATOIRE DE PARIS ECOLE´ DOCTORALE ASTRONOMIE ET ASTROPHYSIQUE D'^ILE-DE-FRANCE Thesis ASTRONOMY AND ASTROPHYSICS Instrumentation Shan Mignot Towards a demonstrator for autonomous object detection on board Gaia (Vers un demonstrateur pour la d´etection autonome des objets `abord de Gaia) Thesis directed by Jean Lacroix then Albert Bijaoui Presented on January 10th 2008 to a jury composed of: Ana G´omez GEPI´ - Observatoire de Paris President Bertrand Granado ETIS - ENSEA Reviewer Michael Perryman ESTEC - Agence Spatiale Europ´eenne Reviewer Daniel Gaff´e LEAT - Universit´ede Nice Sophia-Antipolis Examiner Michel Paindavoine LE2I - Universit´ede Bourgogne Examiner Albert Bijaoui Cassiop´ee- Observatoire de la C^ote d'Azur Director Gregory Flandin EADS Astrium SAS Guest Jean Lacroix LPMA - Universit´eParis 6 Guest Gilles Moury Centre National d'Etudes´ Spatiales Guest Acknowledgements The journey to the stars is a long one. -

Astrometry with Hubble Space Telescope Fine Guidance Sensors a Review1
Astrometry with Hubble Space Telescope Fine Guidance Sensors A Review1 G. Fritz Benedict2, Barbara E. McArthur2, Edmund P. Nelan3, and Thomas E. Harrison4 ABSTRACT Over the last 20 years Hubble Space Telescope Fine Guidance Sensor interfero- metric astrometry has produced precise and accurate parallaxes of astrophysical interesting stars and mass estimates for stellar companions. We review paral- lax results, and binary star and exoplanet mass determinations, and compare a subset of these parallaxes with preliminary Gaia results. The approach to single- field relative astrometry described herein may continue to have value for targets fainter than the Gaia limit in the coming era of 20-30m telescopes. Subject headings: astrometry | instrumentation: interferometers | techniques: interferometric | stars:distances | stars:low-mass | stars:planetary systems | exoplanets:mass 1. Introduction With Gaia poised to expand the astrometric reach of our species by many orders of magnitude (Cacciari et al. 2015), this article serves to highlight the far more modest, but nonetheless useful contributions made by Hubble Space Telescope (HST ) over the past 25 years. Several Fine Guidance Sensors (FGS) aboard HST have consistently delivered sci- entific results with sub-millisecond of arc precision in nearly every astronomical arena to which astrometry could contribute. These include parallaxes for astrophysically interesting arXiv:1610.05176v1 [astro-ph.SR] 17 Oct 2016 2McDonald Observatory, University of Texas, Austin, TX 78712 4Department of Astronomy, New Mexico State University, Box 30001, MSC 4500, Las Cruces, NM 88003- 8001 3Space Telescope Science Institute, 3700 San Martin Dr., Baltimore, MD 21218 1Based on observations made with the NASA/ESA Hubble Space Telescope, obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. -

Double-Blind Test Program for Astrometric Planet Detection with Gaia
A&A 482, 699–729 (2008) Astronomy DOI: 10.1051/0004-6361:20078997 & c ESO 2008 Astrophysics Double-blind test program for astrometric planet detection with Gaia S. Casertano1,M.G.Lattanzi2,A.Sozzetti2,3, A. Spagna2, S. Jancart4, R. Morbidelli2, R. Pannunzio2, D. Pourbaix4, and D. Queloz5 1 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA 2 INAF – Osservatorio Astronomico di Torino, via Osservatorio 20, 10025 Pino Torinese, Italy e-mail: [email protected] 3 Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA 4 Institut d’Astronomie et d’Astrophysique, Université Libre de Bruxelles, CP 226, Boulevard du Triomphe, 1050 Bruxelles, Belgium 5 Observatoire de Genève, 51 Ch. de Maillettes, 1290 Sauveny, Switzerland Received 5 November 2007 / Accepted 1 February 2008 ABSTRACT Aims. The scope of this paper is twofold. First, it describes the simulation scenarios and the results of a large-scale, double-blind test campaign carried out to estimate the potential of Gaia for detecting and measuring planetary systems. The identified capabilities are then put in context by highlighting the unique contribution that the Gaia exoplanet discoveries will be able to bring to the science of extrasolar planets in the next decade. Methods. We use detailed simulations of the Gaia observations of synthetic planetary systems and develop and utilize independent software codes in double-blind mode to analyze the data, including statistical tools for planet detection and different algorithms for single and multiple Keplerian orbit fitting that use no a priori knowledge of the true orbital parameters of the systems. -

Microarcsecond Astrometry: Science Highlights from Gaia Arxiv
Microarcsecond Astrometry: Science Highlights from Gaia Anthony G.A. Brown Leiden Observatory, Leiden University, Niels Bohrweg 2, 2333 CA Leiden, The Netherlands; email: [email protected] Xxxx. Xxx. Xxx. Xxx. YYYY. AA:1{61 Keywords https://doi.org/10.1146/((please add astrometry, space vehicles: Gaia, catalogs, surveys article doi)) Copyright © YYYY by Annual Reviews. Abstract All rights reserved Access to microarcsecond astrometry is now routine in the radio, in- frared, and optical domains. In particular the publication of the sec- ond data release from the Gaia mission made it possible for every as- tronomer to work with easily accessible, high-precision astrometry for 1:7 billion sources to 21st magnitude over the full sky. • Gaia provides splendid astrometry but at the limits of the data small systematic errors are present. A good understanding of the Hipparcos/Gaia astrometry concept, and of the data collection and processing, provides insights into the origins of the systematic errors and how to mitigate their effects. • A selected set of results from Gaia highlight the breadth of excit- ing science and unexpected results, from the solar system to the distant universe, to creative uses of the data. • Gaia DR2 provides for the first time a dense sampling of Galactic phase space with high precision astrometry, photometry, and ra- dial velocities, allowing to uncover subtle features in phase space and the observational HR diagram. • In the coming decade, we can look forward to more accurate and richer Gaia data releases, and new photometric and spectroscopic surveys coming online that will provide essential complementary arXiv:2102.11712v2 [astro-ph.IM] 16 Sep 2021 data. -

CPCS 2.0 – New Automatic Tool for Time-Domain Astronomy P
Contrib. Astron. Obs. Skalnat´ePleso 49, 125 { 131, (2019) CPCS 2.0 { new automatic tool for time-domain astronomy P. Zieli´nski1,L.Wyrzykowski 1, K. Rybicki1, Z. Ko laczkowski2;3 y, P. Bru´s3 and P. Miko lajczyk3 1 Warsaw University Astronomical Observatory, Al. Ujazdowskie 4, 00-478 Warsaw, Poland, (E-mail: [email protected]) 2 Nicolaus Copernicus Astronomical Centre, Polish Academy of Sciences, ul. Bartycka 18, 00-716 Warsaw, Poland 3 Astronomical Institute, University of Wroc law, ul. Kopernika 11, 51-622 Wroc law, Poland Received: November 15, 2018; Accepted: February 25 Abstract. The Cambridge Photometric Calibration Server (CPCS) has been designed to respond to the need of automated rapid photometric data calibra- tion and dissemination for transient events, primarily from Gaia space mission. The Calibration Server has been in operation since 2013 and has been used to calibrate around 50 000 observations of hundreds of transients. We present the status of the tool and demonstrate improvements made in the newest ver- sion, which is enhanced with build-in profile photometric measurement. After tests and implementation on the dedicated website, the new Server will be able to combine imaging data from multiple telescopes and is intended to pro- vide science-ready photometric data within minutes from observations. We also present the OPTICON-supported network of telescopes for Gaia alerts follow- up. Key words: time-domain astronomy { photometry { automatic data reduction and calibration { Gaia Science Alerts 1. Introduction Time-Domain Astronomy (TDA) is a rapidly developing field of observational astronomy, which includes studies of both continuously variable (periodic and non-periodic) sources as well as temporally appearing or changing objects. -

Gaia: the Galaxy in Six (And More) Dimensions
Gaia: the Galaxy in six (and more) dimensions Elena Pancino∗ INAF { Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze, Italy SSDC { Space Science data Center, ASI, Via del Politecnico snc, 00133 Roma, Italy Based on the invited interdisciplinary lecture \Gaia: the Galaxy in 6D+ dimensions" given at the COSPAR 42nd assembly held in Pasadena, California, USA, in July 2018. Abstract The ESA cornerstone mission Gaia was successfully launched in 2013, and is now scanning the sky to accurately measure the positions and motions of about two billion point-like sources of 3.V.20.5 mag, with the main goal of reconstructing the 6D phase space structure of the Milky Way. The typical uncertainties in the astrometry will be in the range 30-500 µas. The sky will be repeatedly scanned (70 times on average) for five years or more, adding the time dimension, and the Gaia data are complemented by mmag photometry in three broad bands, plus line-of-sight velocities from medium resolution spectroscopy for brighter stars. This impressive dataset is having a large impact on various areas of astrophysics, from solar system objects to distant quasars, from nearby stars to unresolved galaxies, from binaries and extrasolar planets to light bending experiments. This invited review paper presents an overview of the Gaia mission and describes why, to reach the goal performances in astrometry and to adequately map the Milky Way kinematics, Gaia was also equipped with state-of-the-art photometers and spectrographs, enabling us to explore much more than the 6D phase-space of positions and velocities. -
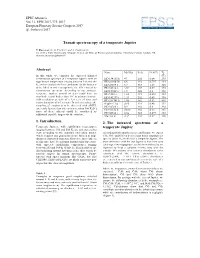
Transit Spectroscopy of a Temperate Jupiter Abstract 1. Introduction 2
EPSC Abstracts Vol. 11, EPSC2017-775, 2017 European Planetary Science Congress 2017 EEuropeaPn PlanetarSy Science CCongress c Author(s) 2017 Transit spectroscopy of a temperate Jupiter T. Encrenaz (1), G. Tinetti (2) and A. Coustenis (1) (1) LESIA, Paris Observatory, Meudon, France, (2) Dept. of Physics and Astronomy, University College London, UK ([email protected]) Abstract Name MP(MJ) P(d) D(AU) TP In this study, we consider the expected infrared (K) transmission spectrum of a temperate Jupiter, with an HD 134113 b 47 202 0.64 295 equilibrium temperature ranging between 350 and 500 HD 233604 b 6.6 192 0.747 434 K, and we analyse the best conditions for the host star HD 28185 b 5.7 383 1.03 320 to be filled in order to optimize the S/N ratio of its HD 32518 b 3.04 157 0.59 395 transmission spectrum. According to our analysis, HD 159243 c 1.9 248 0.8 338 temperate Jupiters around M stars could have an HD 9446 c 1.82 193 0.654 342 -4 amplitude signal higher than 10 in primary transits, HD 141399 c 1.33 202 0.69 390 with revolution periods of a few tens of days and HD 231701 b 1.08 142 0.53 419 transit durations of a few hours. In order to enlarge the Kepler-11 g 0.95 118 0.46 392 sampling of exoplanets to be observed with ARIEL HD 92788 c 0.9 162 0.6 392 (presently focussed on objects warmer than 500 K) [1], HD 37124 b 0.675 154 0.53 331 some of these objects could be considered as HD 45364 c 0.66 343 0.897 252 additional possible targets for the mission. -
![Arxiv:2101.12667V3 [Astro-Ph.EP] 11 May 2021 the Architectures of Stellar, Sub-Stellar, and Planetary Systems Are Relics of Their Formation and Evolutionary Processes](https://docslib.b-cdn.net/cover/4380/arxiv-2101-12667v3-astro-ph-ep-11-may-2021-the-architectures-of-stellar-sub-stellar-and-planetary-systems-are-relics-of-their-formation-and-evolutionary-processes-5124380.webp)
Arxiv:2101.12667V3 [Astro-Ph.EP] 11 May 2021 the Architectures of Stellar, Sub-Stellar, and Planetary Systems Are Relics of Their Formation and Evolutionary Processes
Draft version May 12, 2021 Typeset using LATEX default style in AASTeX63 The Census of Exoplanets in Visual Binaries: population trends from a volume-limited Gaia DR2 and literature search Clémence Fontanive1 and Daniella Bardalez Gagliuffi2 1Center for Space and Habitability, University of Bern, Bern, Switzerland 2American Museum of Natural History, New York, NY, USA (Received November 2, 2020; Accepted January 28, 2021) Submitted to Frontiers in Astronomy and Space Sciences - Exoplanets: The Effect of Stellar Multiplicity on Exoplanetary Systems ABSTRACT We present results from an extensive search in the literature and Gaia DR2 for visual co-moving binary companions to stars hosting exoplanets and brown dwarfs within 200 pc. We found 218 planet hosts out of the 938 in our sample to be part of multiple-star systems, with 10 newly discovered binaries and 2 new tertiary stellar components. This represents an overall raw multiplicity rate of 23:2 ± 1:6 % for hosts to exoplanets across all spectral types, with multi-planet systems found to have a lower stellar duplicity frequency at the 2.2-σ level. We found that more massive hosts are more often in binary configurations, and that planet-bearing stars in multiple systems are predominantly observed to be the most massive component of stellar binaries. Investigations of the multiplicity of planetary systems as a function of planet mass and separation revealed that giant planets with masses above 0.1 MJup are more frequently seen in stellar binaries than small sub-Jovian planets with a 3.6-σ difference, a trend enhanced for the most massive (>7 MJup) short-period (<0.5 AU) planets and brown dwarf companions. -

A Chemical and Kinematical Analysis of the Intermediate-Age Open Cluster IC 166 from APOGEE and Gaia DR2 J
A Chemical and Kinematical Analysis of the Intermediate-age Open Cluster IC 166 from APOGEE and Gaia DR2 J. Schiappacasse-Ulloa, B. Tang, J. Fernández-Trincado, O. Zamora, D. Geisler, P. Frinchaboy, M. Schultheis, F. Dell’agli, S. Villanova, T. Masseron, et al. To cite this version: J. Schiappacasse-Ulloa, B. Tang, J. Fernández-Trincado, O. Zamora, D. Geisler, et al.. A Chemical and Kinematical Analysis of the Intermediate-age Open Cluster IC 166 from APOGEE and Gaia DR2. Astronomical Journal, American Astronomical Society, 2018, 156 (3), pp.94. 10.3847/1538- 3881/aad048. hal-02023251 HAL Id: hal-02023251 https://hal.archives-ouvertes.fr/hal-02023251 Submitted on 8 Dec 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. The Astronomical Journal, 156:94 (14pp), 2018 September https://doi.org/10.3847/1538-3881/aad048 © 2018. The American Astronomical Society. A Chemical and Kinematical Analysis of the Intermediate-age Open Cluster IC 166 from APOGEE and Gaia DR2 J. Schiappacasse-Ulloa1 , B. Tang1,2, J. G. Fernández-Trincado1,3, O. Zamora4,5, D. Geisler1 , P. Frinchaboy6 , M. Schultheis7 , F. Dell’Agli4,5, S. Villanova1 , T. -

Gaia Factsheet
Gaia’s camera is the most powerful ever to be flown in space GAIA FACTSHEET • The accuracy of the camera is equivalent to being able to measure the width of "We have a mission, it is working and I am convinced that it will totally change astronomy" an astronauts’ thumbnail from Earth when the astronaut is on the Moon. Timo Prusti, Gaia Project Scientist (June 2014) • Gaia can measure the positions of objects that are 400 000 times fainter than can be seen with the naked eye. Gaia has started to make the largest, most precise • The Gaia pixel is one of the most complicated ever manufactured. 3D map of our Galaxy One billion stars • Gaia has a unique role to play in the global family of major telescopes. It is a survey telescope that will map the entire sky, rather than observing small patches of sky in depth. 8 megapixels 1000 megapixels (1 billion pixels) • Gaia will map the positions, velocities and properties of 1 billion stars - all the way to the galactic centre and beyond. 1 CCD the size of a fingernail 106 CCDs on board, each measuring • Each of those one billion stars will be observed about 70 times over the five year 6 cm x 4.5 cm, arranged in a focal plane mission – making an average of 40 million observations every day. half a square metre in area • 1 billion stars is about 1% of our Milky Way galaxy. • Gaia is likely to detect tens of thousands of asteroids, comets, failed stars, Gaia is a fully European mission variable stars, exploded stars, star clusters, visible galaxies and exoplanets. -

Gaia 8: Discovery of a Star Cluster Containing Β Lyrae U
A&A 630, L8 (2019) Astronomy https://doi.org/10.1051/0004-6361/201936595 & c ESO 2019 Astrophysics LETTER TO THE EDITOR Gaia 8: Discovery of a star cluster containing β Lyrae U. Bastian Zentrum für Astronomie (Center for Astronomy), Heidelberg University, Mönchhofstr. 14, 69120 Heidelberg, Germany e-mail: [email protected] Received 28 August 2019 / Accepted 11 September 2019 ABSTRACT Aims. The aim here is to try and clarify whether there are stars in the neighbourhood of β Lyrae which are physically connected to the famous prototype eclipsing binary. Methods. We scrutinised the astrometric and photometric data (from Hipparcos and Gaia DR2) of stars in a limited sky field around β Lyrae. Results. A star cluster of about 100 members was discovered, nicely centred on β Lyrae in five dimensions. There are clear indications that the newly discovered cluster belongs to a larger old (extinct) star formation complex, including two known star clusters and an extended, strewn field of stars at practically the same distance and space velocity. Conclusions. This discovery opens up the possibility of determining a precise distance and precise age for β Lyrae using the combined properties of the cluster members. This in turn may form an important basis for an improved astrophysical interpretation of the model binary β Lyrae and its kin. The larger old star formation complex is of scientific interest in its own right. Key words. binaries: general – stars: individual: β Lyrae – open clusters and associations: individual: Gaia 8 – open clusters and associations: individual: Stephenson 1 – open clusters and associations: individual: KPR2005 100 1. -
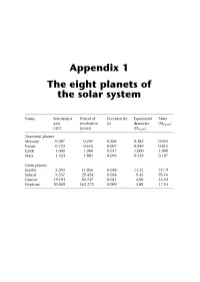
Appendix 1 the Eight Planets of the Solar System
Appendix 1 The eight planets of the solar system Name Semimajor Period of Eccentricity Equatorial Mass axis revolution ie) diameter (MEarth) (AU) (years) (DEarth) Terrestrial planets Mercury 0.387 0.241 0.206 0.382 0.055 Venus 0.723 0.615 0.007 0.949 0.815 Earth 1.000 1.000 0.017 1.000 1.000 Mars 1.524 1.881 0.093 0.532 0.107 Giant planets Jupiter 5.203 11.856 0.048 11.21 317.9 Saturn 9.537 29.424 0.054 9.45 95.16 Uranus 19.191 83.747 0.047 4.00 14.53 Neptune 30.069 163.273 0.009 3.88 17.14 Appendix 2 The first 200 extrasolar planets Name Mass Period Semimajor axis Eccentricity (Mj) (years) (AU) (e) 14 Her b 4.74 1,796.4 2.8 0.338 16 Cyg B b 1.69 798.938 1.67 0.67 2M1207 b 5 46 47 Uma b 2.54 1,089 2.09 0.061 47 Uma c 0.79 2,594 3.79 0 51 Pegb 0.468 4.23077 0.052 0 55 Cnc b 0.784 14.67 0.115 0.0197 55 Cnc c 0.217 43.93 0.24 0.44 55 Cnc d 3.92 4,517.4 5.257 0.327 55 Cnc e 0.045 2.81 0.038 0.174 70 Vir b 7.44 116.689 0.48 0.4 AB Pic b 13.5 275 BD-10 3166 b 0.48 3.488 0.046 0.07 8 Eridani b 0.86 2,502.1 3.3 0.608 y Cephei b 1.59 902.26 2.03 0.2 GJ 3021 b 3.32 133.82 0.49 0.505 GJ 436 b 0.067 2.644963 0.0278 0.207 Gl 581 b 0.056 5.366 0.041 0 G186b 4.01 15.766 0.11 0.046 Gliese 876 b 1.935 60.94 0.20783 0.0249 Gliese 876 c 0.56 30.1 0.13 0.27 Gliese 876 d 0.023 1.93776 0.0208067 0 GQ Lup b 21.5 103 HD 101930 b 0.3 70.46 0.302 0.11 HD 102117 b 0.14 20.67 0.149 0.06 HD 102195 b 0.488 4.11434 0.049 0.06 HD 104985 b 6.3 198.2 0.78 0.03 1 70 The first 200 extrasolar planets Name Mass Period Semimajor axis Eccentricity (Mj) (years) (AU) (e) HD 106252