DOCSLIB.ORG

From Planet Detection to Planet Parameters

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

From Planet Detection to Planet Parameters Michael Perryman Heidelberg (ZAH/MPIA), currently University of Bristol Heraeus Conference, 6 June 2011 Monday, June 6, 2011 1 Star accretion Total: 494 planets Planet Detection November 2010 Miscellaneous Colliding Methods planetesimals Radio Dynamical e!ects Photometry magnetospheresemission Microlensing Protoplanetary Timing disks Decreasing (ground) Astrometry Imaging planet mass Radial velocity Sub Doppler Re"ected dwarfs Pulsars Radio variability light White Binary Optical dwarfs eclipses masses, Transits Astrometric Photometric 10MJ Δi for multiples survival Space Ground 1 5 12 M J Ground sizes, densities, Slow (adaptive Free atmospheres 81 Bound optics) Space Ground "oating 10M๨ Millisec masses sin i, unbiasedGround/ host star Space × space statistics (coronagraphy/ 22 Timing M๨ 4 resonances interferometry) residuals Discovered: 10 planets 358 planets 11 planets 12 planets 103 planets 10 planets 461planets 4 planets 11 planets 12 planets 108 planets Detected: (6 systems, (390 systems, (10 systems, (10 systems, (7 systems, 3 multiple) 45 multiple) 1 multiple) 1 multiple) 1 multiple transit) existing capability projected (10–20 yr) n = planets known discoveries follow-up detections Monday, June 6, 2011 2 Topics • radial velocities • astrometry • transits • internal structure and composition • radio emission • population synthesis Monday, June 6, 2011 3 Monday, June 6, 2011 GJ 581 GJ 876 HD 40307 BD –08 2823 HD 181433 HD 45364 HD 128311 HD 69830 HD 37124 HD 155358 The distribution of multiple systems multiple distribution of The HD 215497 HD 147018 61 Vir increasing host star mass star host increasing HD 108874 55 Cnc HD 190360 HIP 14810 HD 47186 HD 9446 HD 168443 HD 73526 HD 187123 HD 134987 47 UMa HD 202206 HD 125612 HD 11964 HD 217107 HD 183263 HD 82943 HD 12661 µ Ara HAT–P–13 HD 74156 υ And HD 169830 HD 60532 HD 200964 HD 38529 24 Sex BD +20 2457 0.1 1 10 Semi-major axis, a (AU) 4 Numerous of these multiple systems are in resonance... For a heuristic physical description, see Peale (1976), ARA&A 14, 215 Many other types of resonance... An object’s mean motion, n ≣ 2π/P • spin-orbit mean motion resonances (P1/P2 ∼ i/j): • tidal locking (1:1) 2:1, 3:1, 4:1, 5:1, 5:2, etc • Mercury (3:2) • Kozai resonance (e versus i) • Lagrange (1:1) resonance • retrograde resonances... Monday, June 6, 2011 5 Mean motion resonances come in many different flavours, e.g. for the 2:1 (1) unstable 2:1 conjunctions at pericentre (2b) apsidal corotation apsidal alignment (2) stable 2:1 rotates (usually (aligned) conjunctions with libration) at apocentre aligned (symmetric) (3) stable 2:1 (anti-aligned) conjunctions or anti-aligned conjunctions (anti-symmetric) at pericentre aligned (symmetric) both may corotate and/or librate (4) stable 2:1 (2a) apsidal b libration apsidal libration (asymmetric) (small libration asymmetric a angle ⇔ deep apsidal a’ resonance) con!guration b’ Monday, June 6, 2011 6 ... and the first triple (Laplace) resonance (a) Galilean satellites of Jupiter PI = 1.769 138 d Ga PE = 3.551 181 d ny m PG = 7.154 553 d Eu e ro d I p e o a (a) Galilean satellites of Jupiter PI = 1.769 138 d Ga PE = 3.551 181 d ny m PG = 7.154 553 d Eu e ro d t = 0 Io p e t = 3P a t = PI t = 2PI I P = 30.4 d (b) GJ 876 planets b, c, e c n(Io) - 3n(Europa) + 2n(Ganymede) = 0 ... to 9 significant digits, Peale (1976), ARA&AP b14, = 61.1 215 d Pe = 126.6 d t = 0 t = P t = 2P t = 3PI c b I I P = 30.4 d e(b) GJ 876 planetsd b, c, e c 3.48˚ 6.97˚ 10.45˚Pb = 61.1 d Pe = 126.6 d t = 0 c b t = PC t = 2PC t = 3PC e d 3.48˚ 6.97˚ 10.45˚ t = 0 t = PC t = 2PC t = 3PC Rivera et al (2010): ApJ 719, 890 Monday, June 6, 2011 7 Question: how do planets get into resonance? Answer: differential (convergent) migration in the residual gas disk Sándor et al (2010), A&A 517, A31 Monday, June 6, 2011 8 Topics • radial velocities • astrometry • transits • internal structure and composition • radio emission • population synthesis Monday, June 6, 2011 9 Astrometry... 104 150 HR 8799d 1000 1 mas 2012.8 Gl 876 as) µ ( HD 162020 α 100 HD 41004 100 2011.6 pc 10–200 Jupiter Saturn 10–200 pc Saturn 10–200 10 PSR 1620–26 Declination (mas) Declination 50 OGLE-06-109 1 1 µas Astrometric signature, 0.2 yr 12 yr Earth 20 pc 0.1 OGLE–05–169 2010.4 0 Earth 100 pc OGLE–05–390 0.01 0 50 100 0.001 0.01 0.1 1 10 100 Right ascension (mas) Orbital period (years) Effect on the star’s motion around But the size of the effect is small... the barycentre Monday, June 6, 2011 10 ν And observed with the Hubble Space Telescope Fine Guidance Sensors radial velocity orbit + astrometric displacement = orbit inclination 2.0 4 (a) (b) (c) 2 2004 2 1.5 ν And d (mas) 0 α 1 X residuals (mas) X residuals –2 1.0 4 0 2005 2002 (mas) 2003 y 2006 ν And c 2 –1 0.5 0 Astrometric signature, signature, Astrometric ν And ν And b –2 Y residuals (mas) Y residuals –2 0.0 0 8 16 24 32 40 400 800 1200 1600 –2 –1 0 1 2 Inclination (˚) JD – 2 452 000 (d) x (mas) gives a (large) mutual inclination between planet orbits of Δcd = 29.9 deg McArthur et al (2010): ApJ 715, 1203 Important for determining statistics of co-planarity, as inputs to theories of formation and dynamical stability (in future: Gaia, PRIMA) Monday, June 6, 2011 11 Planet mandalas... .. and the nature of the solar dynamo (a) Sun 4 planets, 60 yr (b) µ Ara 4 planets, 30 yr (c) HD 37124 3 planets, 30 yr 2020 2010 1970 1990 2030 1980 2000 –0.008 –0.004 0 0.004 0.008 –0.01 0 0.01 –0.002 0 0.002 0.004 Displacement (AU) Displacement (AU) Displacement (AU) ... exoplanets may allow verification whether angular momentum changes are responsible for some of the solar activity modulations (Perryman & Schulze-Hartung (2011): A&A 525, 65) Monday, June 6, 2011 12 Topics • radial velocities • astrometry • transits • internal structure and composition • radio emission • population synthesis Monday, June 6, 2011 13 Transits 1 2 3 4 !ux b R* = a cos i !ux = star + planet secondary eclipse ux Increasing ! tT time ΔF transit tF The transiting systems have proven of great importance: for densities from absolute masses + accurate radii atmospheric probes from transits and secondary eclipses Monday, June 6, 2011 14 Transit photometry: example state-of-the-art WASP–17 b 0.0 ux ! 1.00 –0.01 0.99 erential magnitude erential ! Di 0.98 –0.02 Relative u’ (326-386 nm) CoRoT−1 1.0002 0.0 ux ! 1.0001 –0.01 erential magnitude erential ! Di 1.0000 Relative Relative –0.02 g’ (413-551 nm) 0.9999 0.0 0.0 0.2 0.4 0.6 0.8 1.0 Orbital phase –0.01 erential magnitude erential ! Di transit transit –0.02 eclipse r’ (557-695 nm) –0.06 –0.04 –0.02 0.0 0.02 0.04 0.06 Orbital phase ...from space, using CoRoT ...from the ground, using ULTRACAM Snellen et al (2009), Nature 459, 543 Bento et al 2011, in preparation Monday, June 6, 2011 15 Principle of transmission & emission spectroscopy Transit: Secondary eclipse: transmission = A−B emission = C−D A B C D star light star light absorbed by re"ected/re-emitted atmosphere by atmosphere area of planetary atmosphere intercepted: annulus of width ∼5H, where Many results (e.g. Spitzer) from, notably HD 209458 and HD 189733: H, H2O, CO2, CH4, Na, etc Monday, June 6, 2011 16 Other transit examples... ) WASP–1 2.520 d WASP–2 2.152 d XO–1 3.942 d ๬ R 1 ( ღ 0 R 1.00 0.98 Flux HAT–P–1 4.465 d HAT–P–2 5.633 d HAT–P–3 2.900 d ) ๬ 1 R ( 0 ღ R 1.00 0.98 Flux ) HAT–P–5 2.788 d HAT–P–6 3.853 d GJ 436 2.644 d ๬ R 1 ( ღ 0 R 1.00 Flux 0.98 –4 –2 0 2 4 –4 –2 0 2 4 –4 –2 0 2 4 Hours Hours Hours Torres et al (2008) ApJ 677, 1324 Monday, June 6, 2011 17 Higher-order effects • from transit light-curve: • stellar density, ρ∗ • planet surface gravity, gp=GMp/Rp • planet limb darkening • higher-order photometric effects: • planet: satellites, rings/comets, planet oblateness, rotation, weather, bow shocks • star: spots, effects of rapid rotation, ellipsoidal variations • higher-order spectroscopic effects: • projected angle between stellar spin axis and planet orbit (Rossiter-McLaughlin) • effects of atmospheric opacity, atmospheric winds • higher-order timing effects: • apsidal precession due to tidal bulges, rotational flattening, general relativity • nodal precession in the case of polar orbits (WASP-33) • effects of planet satellites • effects of other planets, including Trojans • perspective effects due to star’s parallax and proper motion • magnetic breaking, non-gravitational forces (Yarkovsky effect) Monday, June 6, 2011 18 Rossiter-McLaughlin effect Winn et al (2006), ApJ 653, L69 1.01 HD 189733 1.00 ux 0.99 ! 0.98 0.97 Relative Relative C – O b = – 0.5, λ = 0" b = – 0.5, λ = 30" b = – 0.5, λ = 60" –0.04 –0.02 0.0 0.02 0.04 ) 1 − Time since mid-transit (d) + 60 +200 0 ) 1 +100 − – 60 0 Rad (m s velocity –2 –1 0 1 2 –2 –1 0 1 2 –2 –1 0 1 2 #100 Time (h) Time (h) Time (h) #200 Radial (m s velocity O – C –1.0 –0.5 0.0 0.5 1.0 Time since mid-transit (d) +100 ) + 50 some orbits are retrograde 1 − statistics suggest scattering: Triaud et al (2010), A&A 524, 25 0 or scattering + migration: Marchi et al (2009), MNRAS 394, L93 # 50 but not migration alone O – C Monday, June 6, 2011 Radial (m s velocity 19 –0.10 –0.05 0.0 0.05 0.10 Time since mid-transit (d) Other transiting phenomena observed..
Recommended publications
  • Lurking in the Shadows: Wide-Separation Gas Giants As Tracers of Planet Formation

    Lurking in the Shadows: Wide-Separation Gas Giants As Tracers of Planet Formation

    Lurking in the Shadows: Wide-Separation Gas Giants as Tracers of Planet Formation Thesis by Marta Levesque Bryan In Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy CALIFORNIA INSTITUTE OF TECHNOLOGY Pasadena, California 2018 Defended May 1, 2018 ii © 2018 Marta Levesque Bryan ORCID: [0000-0002-6076-5967] All rights reserved iii ACKNOWLEDGEMENTS First and foremost I would like to thank Heather Knutson, who I had the great privilege of working with as my thesis advisor. Her encouragement, guidance, and perspective helped me navigate many a challenging problem, and my conversations with her were a consistent source of positivity and learning throughout my time at Caltech. I leave graduate school a better scientist and person for having her as a role model. Heather fostered a wonderfully positive and supportive environment for her students, giving us the space to explore and grow - I could not have asked for a better advisor or research experience. I would also like to thank Konstantin Batygin for enthusiastic and illuminating discussions that always left me more excited to explore the result at hand. Thank you as well to Dimitri Mawet for providing both expertise and contagious optimism for some of my latest direct imaging endeavors. Thank you to the rest of my thesis committee, namely Geoff Blake, Evan Kirby, and Chuck Steidel for their support, helpful conversations, and insightful questions. I am grateful to have had the opportunity to collaborate with Brendan Bowler. His talk at Caltech my second year of graduate school introduced me to an unexpected population of massive wide-separation planetary-mass companions, and lead to a long-running collaboration from which several of my thesis projects were born.
  • Arxiv:1809.07342V1 [Astro-Ph.SR] 19 Sep 2018

    Arxiv:1809.07342V1 [Astro-Ph.SR] 19 Sep 2018

    Draft version September 21, 2018 Preprint typeset using LATEX style emulateapj v. 11/10/09 FAR-ULTRAVIOLET ACTIVITY LEVELS OF F, G, K, AND M DWARF EXOPLANET HOST STARS* Kevin France1, Nicole Arulanantham1, Luca Fossati2, Antonino F. Lanza3, R. O. Parke Loyd4, Seth Redfield5, P. Christian Schneider6 Draft version September 21, 2018 ABSTRACT We present a survey of far-ultraviolet (FUV; 1150 { 1450 A)˚ emission line spectra from 71 planet- hosting and 33 non-planet-hosting F, G, K, and M dwarfs with the goals of characterizing their range of FUV activity levels, calibrating the FUV activity level to the 90 { 360 A˚ extreme-ultraviolet (EUV) stellar flux, and investigating the potential for FUV emission lines to probe star-planet interactions (SPIs). We build this emission line sample from a combination of new and archival observations with the Hubble Space Telescope-COS and -STIS instruments, targeting the chromospheric and transition region emission lines of Si III,N V,C II, and Si IV. We find that the exoplanet host stars, on average, display factors of 5 { 10 lower UV activity levels compared with the non-planet hosting sample; this is explained by a combination of observational and astrophysical biases in the selection of stars for radial-velocity planet searches. We demonstrate that UV activity-rotation relation in the full F { M star sample is characterized by a power-law decline (with index α ≈ −1.1), starting at rotation periods & 3.5 days. Using N V or Si IV spectra and a knowledge of the star's bolometric flux, we present a new analytic relationship to estimate the intrinsic stellar EUV irradiance in the 90 { 360 A˚ band with an accuracy of roughly a factor of ≈ 2.
  • Catalog of Nearby Exoplanets

    Catalog of Nearby Exoplanets

    Catalog of Nearby Exoplanets1 R. P. Butler2, J. T. Wright3, G. W. Marcy3,4, D. A Fischer3,4, S. S. Vogt5, C. G. Tinney6, H. R. A. Jones7, B. D. Carter8, J. A. Johnson3, C. McCarthy2,4, A. J. Penny9,10 ABSTRACT We present a catalog of nearby exoplanets. It contains the 172 known low- mass companions with orbits established through radial velocity and transit mea- surements around stars within 200 pc. We include 5 previously unpublished exo- planets orbiting the stars HD 11964, HD 66428, HD 99109, HD 107148, and HD 164922. We update orbits for 90 additional exoplanets including many whose orbits have not been revised since their announcement, and include radial ve- locity time series from the Lick, Keck, and Anglo-Australian Observatory planet searches. Both these new and previously published velocities are more precise here due to improvements in our data reduction pipeline, which we applied to archival spectra. We present a brief summary of the global properties of the known exoplanets, including their distributions of orbital semimajor axis, mini- mum mass, and orbital eccentricity. Subject headings: catalogs — stars: exoplanets — techniques: radial velocities 1Based on observations obtained at the W. M. Keck Observatory, which is operated jointly by the Uni- versity of California and the California Institute of Technology. The Keck Observatory was made possible by the generous financial support of the W. M. Keck Foundation. arXiv:astro-ph/0607493v1 21 Jul 2006 2Department of Terrestrial Magnetism, Carnegie Institute of Washington, 5241 Broad Branch Road NW, Washington, DC 20015-1305 3Department of Astronomy, 601 Campbell Hall, University of California, Berkeley, CA 94720-3411 4Department of Physics and Astronomy, San Francisco State University, San Francisco, CA 94132 5UCO/Lick Observatory, University of California, Santa Cruz, CA 95064 6Anglo-Australian Observatory, PO Box 296, Epping.
  • Super Earths and Dynamical Stability of Planetary Systems: First Parallel GPU Simulations Using GENGA

    Super Earths and Dynamical Stability of Planetary Systems: First Parallel GPU Simulations Using GENGA

    Mon. Not. R. Astron. Soc. 000, 000{000 (0000) Printed 27 January 2021 (MN LATEX style file v2.2) Super Earths and Dynamical Stability of Planetary Systems: First Parallel GPU Simulations Using GENGA S. Elser,1 S. L. Grimm,1 J. G. Stadel1 1Universit¨atZ¨urich,Winterthurerstrasse 190, CH-8057 Z¨urich,Switzerland 27 January 2021 ABSTRACT We report on the stability of hypothetical Super-Earths in the habitable zone of known multi-planetary systems. Most of them have not yet been studied in detail concerning the existence of additional low-mass planets. The new N-body code GENGA developed at the UZH allows us to perform numerous N-body simulations in parallel on GPUs. With this numerical tool, we can study the stability of orbits of hypothetical planets in the semi-major axis and eccentricity parameter space in high resolution. Massless test particle simulations give good predictions on the extension of the stable region and show that HIP 14180 and HD 37124 do not provide stable orbits in the habitable zone. Based on these simulations, we carry out simulations of 10M⊕ planets in several systems (HD 11964, HD 47186, HD 147018, HD 163607, HD 168443, HD 187123, HD 190360, HD 217107 and HIP 57274). They provide more exact information about orbits at the location of mean motion resonances and at the edges of the stability zones. Beside the stability of orbits, we study the secular evolution of the planets to constrain probable locations of hypothetical planets. Assuming that planetary systems are in general closely packed, we find that apart from HD 168443, all of the systems can harbor 10 M⊕ planets in the habitable zone.
  • Naming the Extrasolar Planets

    Naming the Extrasolar Planets

    Naming the extrasolar planets W. Lyra Max Planck Institute for Astronomy, K¨onigstuhl 17, 69177, Heidelberg, Germany [email protected] Abstract and OGLE-TR-182 b, which does not help educators convey the message that these planets are quite similar to Jupiter. Extrasolar planets are not named and are referred to only In stark contrast, the sentence“planet Apollo is a gas giant by their assigned scientific designation. The reason given like Jupiter” is heavily - yet invisibly - coated with Coper- by the IAU to not name the planets is that it is consid- nicanism. ered impractical as planets are expected to be common. I One reason given by the IAU for not considering naming advance some reasons as to why this logic is flawed, and sug- the extrasolar planets is that it is a task deemed impractical. gest names for the 403 extrasolar planet candidates known One source is quoted as having said “if planets are found to as of Oct 2009. The names follow a scheme of association occur very frequently in the Universe, a system of individual with the constellation that the host star pertains to, and names for planets might well rapidly be found equally im- therefore are mostly drawn from Roman-Greek mythology. practicable as it is for stars, as planet discoveries progress.” Other mythologies may also be used given that a suitable 1. This leads to a second argument. It is indeed impractical association is established. to name all stars. But some stars are named nonetheless. In fact, all other classes of astronomical bodies are named.
  • Download This Article in PDF Format

    Download This Article in PDF Format

    A&A 562, A92 (2014) Astronomy DOI: 10.1051/0004-6361/201321493 & c ESO 2014 Astrophysics Li depletion in solar analogues with exoplanets Extending the sample, E. Delgado Mena1,G.Israelian2,3, J. I. González Hernández2,3,S.G.Sousa1,2,4, A. Mortier1,4,N.C.Santos1,4, V. Zh. Adibekyan1, J. Fernandes5, R. Rebolo2,3,6,S.Udry7, and M. Mayor7 1 Centro de Astrofísica, Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal e-mail: [email protected] 2 Instituto de Astrofísica de Canarias, C/ Via Lactea s/n, 38200 La Laguna, Tenerife, Spain 3 Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain 4 Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto, 4169-007 Porto, Portugal 5 CGUC, Department of Mathematics and Astronomical Observatory, University of Coimbra, 3049 Coimbra, Portugal 6 Consejo Superior de Investigaciones Científicas, CSIC, Spain 7 Observatoire de Genève, Université de Genève, 51 ch. des Maillettes, 1290 Sauverny, Switzerland Received 18 March 2013 / Accepted 25 November 2013 ABSTRACT Aims. We want to study the effects of the formation of planets and planetary systems on the atmospheric Li abundance of planet host stars. Methods. In this work we present new determinations of lithium abundances for 326 main sequence stars with and without planets in the Teff range 5600–5900 K. The 277 stars come from the HARPS sample, the remaining targets were observed with a variety of high-resolution spectrographs. Results. We confirm significant differences in the Li distribution of solar twins (Teff = T ± 80 K, log g = log g ± 0.2and[Fe/H] = [Fe/H] ±0.2): the full sample of planet host stars (22) shows Li average values lower than “single” stars with no detected planets (60).
  • Arxiv:2105.11583V2 [Astro-Ph.EP] 2 Jul 2021 Keck-HIRES, APF-Levy, and Lick-Hamilton Spectrographs

    Arxiv:2105.11583V2 [Astro-Ph.EP] 2 Jul 2021 Keck-HIRES, APF-Levy, and Lick-Hamilton Spectrographs

    Draft version July 6, 2021 Typeset using LATEX twocolumn style in AASTeX63 The California Legacy Survey I. A Catalog of 178 Planets from Precision Radial Velocity Monitoring of 719 Nearby Stars over Three Decades Lee J. Rosenthal,1 Benjamin J. Fulton,1, 2 Lea A. Hirsch,3 Howard T. Isaacson,4 Andrew W. Howard,1 Cayla M. Dedrick,5, 6 Ilya A. Sherstyuk,1 Sarah C. Blunt,1, 7 Erik A. Petigura,8 Heather A. Knutson,9 Aida Behmard,9, 7 Ashley Chontos,10, 7 Justin R. Crepp,11 Ian J. M. Crossfield,12 Paul A. Dalba,13, 14 Debra A. Fischer,15 Gregory W. Henry,16 Stephen R. Kane,13 Molly Kosiarek,17, 7 Geoffrey W. Marcy,1, 7 Ryan A. Rubenzahl,1, 7 Lauren M. Weiss,10 and Jason T. Wright18, 19, 20 1Cahill Center for Astronomy & Astrophysics, California Institute of Technology, Pasadena, CA 91125, USA 2IPAC-NASA Exoplanet Science Institute, Pasadena, CA 91125, USA 3Kavli Institute for Particle Astrophysics and Cosmology, Stanford University, Stanford, CA 94305, USA 4Department of Astronomy, University of California Berkeley, Berkeley, CA 94720, USA 5Cahill Center for Astronomy & Astrophysics, California Institute of Technology, Pasadena, CA 91125, USA 6Department of Astronomy & Astrophysics, The Pennsylvania State University, 525 Davey Lab, University Park, PA 16802, USA 7NSF Graduate Research Fellow 8Department of Physics & Astronomy, University of California Los Angeles, Los Angeles, CA 90095, USA 9Division of Geological and Planetary Sciences, California Institute of Technology, Pasadena, CA 91125, USA 10Institute for Astronomy, University of Hawai`i,
  • Arxiv:0809.1275V2

    Arxiv:0809.1275V2

    How eccentric orbital solutions can hide planetary systems in 2:1 resonant orbits Guillem Anglada-Escud´e1, Mercedes L´opez-Morales1,2, John E. Chambers1 [email protected], [email protected], [email protected] ABSTRACT The Doppler technique measures the reflex radial motion of a star induced by the presence of companions and is the most successful method to detect ex- oplanets. If several planets are present, their signals will appear combined in the radial motion of the star, leading to potential misinterpretations of the data. Specifically, two planets in 2:1 resonant orbits can mimic the signal of a sin- gle planet in an eccentric orbit. We quantify the implications of this statistical degeneracy for a representative sample of the reported single exoplanets with available datasets, finding that 1) around 35% percent of the published eccentric one-planet solutions are statistically indistinguishible from planetary systems in 2:1 orbital resonance, 2) another 40% cannot be statistically distinguished from a circular orbital solution and 3) planets with masses comparable to Earth could be hidden in known orbital solutions of eccentric super-Earths and Neptune mass planets. Subject headings: Exoplanets – Orbital dynamics – Planet detection – Doppler method arXiv:0809.1275v2 [astro-ph] 25 Nov 2009 Introduction Most of the +300 exoplanets found to date have been discovered using the Doppler tech- nique, which measures the reflex motion of the host star induced by the planets (Mayor & Queloz 1995; Marcy & Butler 1996). The diverse characteristics of these exoplanets are somewhat surprising. Many of them are similar in mass to Jupiter, but orbit much closer to their 1Carnegie Institution of Washington, Department of Terrestrial Magnetism, 5241 Broad Branch Rd.
  • The Maunder Minimum and the Variable Sun-Earth Connection

    The Maunder Minimum and the Variable Sun-Earth Connection

    The Maunder Minimum and the Variable Sun-Earth Connection (Front illustration: the Sun without spots, July 27, 1954) By Willie Wei-Hock Soon and Steven H. Yaskell To Soon Gim-Chuan, Chua Chiew-See, Pham Than (Lien+Van’s mother) and Ulla and Anna In Memory of Miriam Fuchs (baba Gil’s mother)---W.H.S. In Memory of Andrew Hoff---S.H.Y. To interrupt His Yellow Plan The Sun does not allow Caprices of the Atmosphere – And even when the Snow Heaves Balls of Specks, like Vicious Boy Directly in His Eye – Does not so much as turn His Head Busy with Majesty – ‘Tis His to stimulate the Earth And magnetize the Sea - And bind Astronomy, in place, Yet Any passing by Would deem Ourselves – the busier As the Minutest Bee That rides – emits a Thunder – A Bomb – to justify Emily Dickinson (poem 224. c. 1862) Since people are by nature poorly equipped to register any but short-term changes, it is not surprising that we fail to notice slower changes in either climate or the sun. John A. Eddy, The New Solar Physics (1977-78) Foreword By E. N. Parker In this time of global warming we are impelled by both the anticipated dire consequences and by scientific curiosity to investigate the factors that drive the climate. Climate has fluctuated strongly and abruptly in the past, with ice ages and interglacial warming as the long term extremes. Historical research in the last decades has shown short term climatic transients to be a frequent occurrence, often imposing disastrous hardship on the afflicted human populations.
  • Today in Astronomy 106: Exoplanets

    Today in Astronomy 106: Exoplanets

    Today in Astronomy 106: exoplanets The successful search for extrasolar planets Prospects for determining the fraction of stars with planets, and the number of habitable planets per planetary system (fp and ne). T. Pyle, SSC/JPL/Caltech/NASA. 26 May 2011 Astronomy 106, Summer 2011 1 Observing exoplanets Stars are vastly brighter and more massive than planets, and most stars are far enough away that the planets are lost in the glare. So astronomers have had to be more clever and employ the motion of the orbiting planet. The methods they use (exoplanets detected thereby): Astrometry (0): tiny wobble in star’s motion across the sky. Radial velocity (399): tiny wobble in star’s motion along the line of sight by Doppler shift. Timing (9): tiny delay or advance in arrival of pulses from regularly-pulsating stars. Gravitational microlensing (10): brightening of very distant star as it passes behind a planet. 26 May 2011 Astronomy 106, Summer 2011 2 Observing exoplanets (continued) Transits (69): periodic eclipsing of star by planet, or vice versa. Very small effect, about like that of a bug flying in front of the headlight of a car 10 miles away. Imaging (11 but 6 are most likely to be faint stars): taking a picture of the planet, usually by blotting out the star. Of these by far the most useful so far has been the combination of radial-velocity and transit detection. Astrometry and gravitational microlensing of sufficient precision to detect lots of planets would need dedicated, specialized observatories in space. Imaging lots of planets will require 30-meter-diameter telescopes for visible and infrared wavelengths.
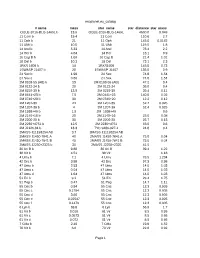
  • Exoplanet.Eu Catalog Page 1 # Name Mass Star Name

    Exoplanet.Eu Catalog Page 1 # Name Mass Star Name

    exoplanet.eu_catalog # name mass star_name star_distance star_mass OGLE-2016-BLG-1469L b 13.6 OGLE-2016-BLG-1469L 4500.0 0.048 11 Com b 19.4 11 Com 110.6 2.7 11 Oph b 21 11 Oph 145.0 0.0162 11 UMi b 10.5 11 UMi 119.5 1.8 14 And b 5.33 14 And 76.4 2.2 14 Her b 4.64 14 Her 18.1 0.9 16 Cyg B b 1.68 16 Cyg B 21.4 1.01 18 Del b 10.3 18 Del 73.1 2.3 1RXS 1609 b 14 1RXS1609 145.0 0.73 1SWASP J1407 b 20 1SWASP J1407 133.0 0.9 24 Sex b 1.99 24 Sex 74.8 1.54 24 Sex c 0.86 24 Sex 74.8 1.54 2M 0103-55 (AB) b 13 2M 0103-55 (AB) 47.2 0.4 2M 0122-24 b 20 2M 0122-24 36.0 0.4 2M 0219-39 b 13.9 2M 0219-39 39.4 0.11 2M 0441+23 b 7.5 2M 0441+23 140.0 0.02 2M 0746+20 b 30 2M 0746+20 12.2 0.12 2M 1207-39 24 2M 1207-39 52.4 0.025 2M 1207-39 b 4 2M 1207-39 52.4 0.025 2M 1938+46 b 1.9 2M 1938+46 0.6 2M 2140+16 b 20 2M 2140+16 25.0 0.08 2M 2206-20 b 30 2M 2206-20 26.7 0.13 2M 2236+4751 b 12.5 2M 2236+4751 63.0 0.6 2M J2126-81 b 13.3 TYC 9486-927-1 24.8 0.4 2MASS J11193254 AB 3.7 2MASS J11193254 AB 2MASS J1450-7841 A 40 2MASS J1450-7841 A 75.0 0.04 2MASS J1450-7841 B 40 2MASS J1450-7841 B 75.0 0.04 2MASS J2250+2325 b 30 2MASS J2250+2325 41.5 30 Ari B b 9.88 30 Ari B 39.4 1.22 38 Vir b 4.51 38 Vir 1.18 4 Uma b 7.1 4 Uma 78.5 1.234 42 Dra b 3.88 42 Dra 97.3 0.98 47 Uma b 2.53 47 Uma 14.0 1.03 47 Uma c 0.54 47 Uma 14.0 1.03 47 Uma d 1.64 47 Uma 14.0 1.03 51 Eri b 9.1 51 Eri 29.4 1.75 51 Peg b 0.47 51 Peg 14.7 1.11 55 Cnc b 0.84 55 Cnc 12.3 0.905 55 Cnc c 0.1784 55 Cnc 12.3 0.905 55 Cnc d 3.86 55 Cnc 12.3 0.905 55 Cnc e 0.02547 55 Cnc 12.3 0.905 55 Cnc f 0.1479 55
  • Ghost Imaging of Space Objects

    Ghost Imaging of Space Objects

    Ghost Imaging of Space Objects Dmitry V. Strekalov, Baris I. Erkmen, Igor Kulikov, and Nan Yu Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, California 91109-8099 USA NIAC Final Report September 2014 Contents I. The proposed research 1 A. Origins and motivation of this research 1 B. Proposed approach in a nutshell 3 C. Proposed approach in the context of modern astronomy 7 D. Perceived benefits and perspectives 12 II. Phase I goals and accomplishments 18 A. Introducing the theoretical model 19 B. A Gaussian absorber 28 C. Unbalanced arms configuration 32 D. Phase I summary 34 III. Phase II goals and accomplishments 37 A. Advanced theoretical analysis 38 B. On observability of a shadow gradient 47 C. Signal-to-noise ratio 49 D. From detection to imaging 59 E. Experimental demonstration 72 F. On observation of phase objects 86 IV. Dissemination and outreach 90 V. Conclusion 92 References 95 1 I. THE PROPOSED RESEARCH The NIAC Ghost Imaging of Space Objects research program has been carried out at the Jet Propulsion Laboratory, Caltech. The program consisted of Phase I (October 2011 to September 2012) and Phase II (October 2012 to September 2014). The research team consisted of Drs. Dmitry Strekalov (PI), Baris Erkmen, Igor Kulikov and Nan Yu. The team members acknowledge stimulating discussions with Drs. Leonidas Moustakas, Andrew Shapiro-Scharlotta, Victor Vilnrotter, Michael Werner and Paul Goldsmith of JPL; Maria Chekhova and Timur Iskhakov of Max Plank Institute for Physics of Light, Erlangen; Paul Nu˜nez of Coll`ege de France & Observatoire de la Cˆote d’Azur; and technical support from Victor White and Pierre Echternach of JPL.