El Modelo Lineal Sin T ´Ermino Independiente Y El Coeficiente De
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

STAT 3304/5304 Introduction to Statistical Computing
STAT 3304/5304 Introduction to Statistical Computing Statistical Packages Some Statistical Packages • BMDP • GLIM • HIL • JMP • LISREL • MATLAB • MINITAB 1 Some Statistical Packages • R • S-PLUS • SAS • SPSS • STATA • STATISTICA • STATXACT • . and many more 2 BMDP • BMDP is a comprehensive library of statistical routines from simple data description to advanced multivariate analysis, and is backed by extensive documentation. • Each individual BMDP sub-program is based on the most competitive algorithms available and has been rigorously field-tested. • BMDP has been known for the quality of it’s programs such as Survival Analysis, Logistic Regression, Time Series, ANOVA and many more. • The BMDP vendor was purchased by SPSS Inc. of Chicago in 1995. SPSS Inc. has stopped all develop- ment work on BMDP, choosing to incorporate some of its capabilities into other products, primarily SY- STAT, instead of providing further updates to the BMDP product. • BMDP is now developed by Statistical Solutions and the latest version (BMDP 2009) features a new mod- ern user-interface with all the statistical functionality of the classic program, running in the latest MS Win- dows environments. 3 LISREL • LISREL is software for confirmatory factor analysis and structural equation modeling. • LISREL is particularly designed to accommodate models that include latent variables, measurement errors in both dependent and independent variables, reciprocal causation, simultaneity, and interdependence. • Vendor information: Scientific Software International http://www.ssicentral.com/ 4 MATLAB • Matlab is an interactive, matrix-based language for technical computing, which allows easy implementation of statistical algorithms and numerical simulations. • Highlights of Matlab include the number of toolboxes (collections of programs to address specific sets of problems) available. -

Visualizing Multivariate Data: Graphs That Tell Stories
IASE 2020 Roundtable Paper – Refereed Engel, Campos, Nicholson, Ridgway & Teixeira VISUALIZING MULTIVARIATE DATA: GRAPHS THAT TELL STORIES Joachim Engel1, Pedro Campos2, James Nicholson3, Jim Ridgway3, and Sónia Teixeira2 1Ludwigsburg University of Education, Germany 2University of Porto, Portugal 3University of Durham, UK [email protected] Important statistical ideas can be introduced via visualizations without heavy mathematics, hence can become accessible to a broader citizenry. Along a few selected examples, from historical to modern, with technology-based data visualizations, we highlight the potential of data visualizations to enhance students’ capacity to reason with complex data and discuss the role of visualization as a tool to strengthen civic participation in democracy. BACKGROUND Visual representations are a central means of conveying information, illuminating facts, supporting the user in recognizing patterns and gaining insights into difficult concepts (see, e.g., Chambers et al., 1983; Chance et al., 2007; Tishkovskaja & Lancaster, 2012). A Graph can provide a compelling approach to statistical thinking that focuses on important concepts rather than formal mathematics and procedures (Biehler, 1993; Nolan & Perrett, 2016). Graphical methods provide powerful diagnostic tools for confirming assumptions, or, when assumptions are not met for suggesting corrective actions. Therefore, creating meaningful data visualizations to communicate information is an important skill in its own right. It is an important mean of informing citizens about governance and presenting evidence about the state of the world in order to raise awareness for injustices and structural social inequalities or burning problems like global warming or demographic change.The simulation to illustrate the outbreak of COVID-19 and the effect of social distancing, published by the Washington Post, is another striking example (see https://www.washingtonpost.com/graphics/2020/world/corona-simulator/). -

Recent Statistical Software
PRODUCT LISTING Recent Statistical Software The following infonnation is from press releases or other material provided by publishers. DOS SYSTAT Version 5.0 Documentation for DOS SYSTAT 5.0 is entirely re SYSTAT, Inc., announces the release ofSYSTAT Ver written and is in four paperback manuals-Getting Staned, sion 5.0, a comprehensive statistical analysis, data man Data, Graphics, and Statistics. Each chapter introduces agement, and graphics software package for ffiM PCIATs the statistical concepts behind the procedure, with step and DOS-compatible systems with 640K RAM and a by-step instructions and examples. Tips and shortcuts give hard disk. hints that make new users productive quickly. SYSTAT Version 5.0 integrates graphics and analysis SYSTAT Version 5.0 requires an ffiM-eompatible sys procedures through its menu-driven interface. New pull tem running MS/PC-DOS 3.0 or higher, with 640K RAM down hierarchical menus organize procedures intuitively, and at least a 20MB hard disk. SYSTAT supports all com with a command window available at any time should the mon video displays and popular hard-eopy devices such user wish to edit commands. Context-sensitive help is as the HP Laserjet, ffiM and HP plotters, Epson, Toshiba, available throughout. All graphics procedures support and other printers. DOS SYSTAT Version 5.0 costs $895. color output, with default settings fully controllable by Current users ofSYSTAT on DOS systems may upgrade the user. to Version 5.0 for $195. In addition to standard graphs, plots, bar charts, histo For more infonnation, contact SYSTAT, Inc., 1800 grams, and scatterplots, DOS SYSTAT 5.0 features Sherman Ave., Suite 801, Evanston, IL60201 (phone: 708 graphs rarely found in other commercial packages. -

Cumulation of Poverty Measures: the Theory Beyond It, Possible Applications and Software Developed
Cumulation of Poverty measures: the theory beyond it, possible applications and software developed (Francesca Gagliardi and Giulio Tarditi) Siena, October 6th , 2010 1 Context and scope Reliable indicators of poverty and social exclusion are an essential monitoring tool. In the EU-wide context, these indicators are most useful when they are comparable across countries and over time. Furthermore, policy research and application require statistics disaggregated to increasingly lower levels and smaller subpopulations. Direct, one-time estimates from surveys designed primarily to meet national needs tend to be insufficiently precise for meeting these new policy needs. This is particularly true in the domain of poverty and social exclusion, the monitoring of which requires complex distributional statistics – statistics necessarily based on intensive and relatively small- scale surveys of households and persons. This work addresses some statistical aspects relating to improving the sampling precision of such indicators in EU countries, in particular through the cumulation of data over rounds of regularly repeated national surveys. 2 EU-SILC The reference data for this purpose are EU Statistics on Income and Living Conditions, the major source of comparative statistics on income and living conditions in Europe. A standard integrated design has been adopted by nearly all EU countries. It involves a rotational panel, with a new sample of households and persons introduced each year to replace one-fourth of the existing sample. Persons enumerated in each new sample are followed-up in the survey for four years. The design yields each year a cross- sectional sample, as well as longitudinal samples of 2, 3 and 4 year duration. -

A Review of Two Different Approaches for the Analysis of Growth Data Using
THE STATISTICAL SOFTWARENEWSLETTER 583 A review of two different approaches for the analysis of growth data using longitudinal mixed linear models: Comparing hierarchical linear regression (ML3, HLM) and repeated measures designs with structured covariance matrices (BMDP5V) Rien van der Leeden 1), Karen Vrijburg 1) & Jan de Leeuw~) 1~Department of Psychometrics and Research Methodology, University of Leiden, Postbus 9555, 2300 RB Leiden,The Netherlands 2)UCLA Department of Statistics, University of California at Los Angeles, USA Abstract: In this paper we review two approaches for method to handle growth data, theoretically, as well as the analysis of growth data by means of longitudinal in a practical sense. For the most part, shortcomings mixed linear models. In these models the individual are induced by the accompanying software, developed growth parameters, (most often) specifying polynomial within different scientific traditions. Applied to com- growth curves, may vary randomly across individuals. parable problems, the three programs produce This variation may in turn be accounted for by explain- equivalent results. ing variables. Keywords: Multilevel analysis, Mixed linear models, The first approach we discuss, is a type of multilevel MANOVA, Repeated mesaures, Growth curve models, model in which growth data are treated as having a hi- Structured covariance matrices. erarchical slructure: measurements are 'nested' within (SSNinCSDA 20, 583-605 (1996)) individuals. The second is a version of a MANOVA repeated measures model employing a structured Received: March 1995 Revised: February 1996 (error)covariance matrix. Of both approaches we ex- amine the underlying statistical models and their inter- I. Introduction relations. Apart from this theoretical comparison we review software by which they can be applied for real In social science one frequently encounters re- data analysis: two multilevel programs, ML3 and search situations in which individuals are meas- HLM, and one repeated measures program, BMDP5V. -

Porcelain & Ceramic Products (B2B Procurement)
Porcelain & Ceramic Products (B2B Procurement) Purchasing World Report Since 1979 www.datagroup.org Porcelain & Ceramic Products (B2B Procurement) Porcelain & Ceramic Products (B2B Procurement) 2 B B Purchasing World Report Porcelain & Ceramic Products (B2B Procurement) The Purchasing World Report is an extract of the main database and provides a number of limited datasets for each of the countries covered. For users needing more information, detailed data on Porcelain & Ceramic Products (B2B Procurement) is available in several Editions and Database versions. Users can order (at a discount) any other Editions, or the Database versions, as required from the After-Sales Service or from any Dealer. This research provides data the Buying of Materials, Products and Services used for Porcelain & Ceramic Products. Contents B2B Purchasing World Report ................................................................................................................................... 2 B2B Purchasing World Report Specifications ............................................................................................................ 4 Materials, Products and Services Purchased : US$ ........................................................................................... 4 Report Description .................................................................................................................................................. 6 Tables .................................................................................................................................................................... -

(Microsoft Powerpoint
Acil T ıp’ta İstatistik Sunum Plan ı IV. Acil Tıp Asistan Sempozyumu 19-21 Haziran 2009 Biyoistatistik nedir Sa ğlık alan ında biyoistatistik Acil T ıp’ta biyoistatistik Meral Leman Almac ıoğlu İstatistik yaz ılım programlar ı Uluda ğ Üniversitesi T ıp Fakültesi Acil T ıp AD Bursa Biyoistatistik Nedir Biyoistatistik Niçin Gereklidir 1. Biyolojik, laboratuar ve klinik verilerdeki yayg ınl ık ı ğ ı Biyoistatistik; t p ve sa l k bilimleri 2. Verilerin anla şı lmas ı alanlar ında veri toplanmas ı, özetleme, 3. Yorumlanmas ı analiz ve de ğerlendirmede istatistiksel 4. Tıp literatürünün kriti ğinin yap ılmas ı yöntemleri kullanan bilim dal ı 5. Ara ştırmalar ın planlanmas ı, gerçekle ştirilmesi, analiz ve yorumlanmas ı Biyoistatistiksel teknikler kullan ılmadan gerçekle ştirilen ara ştırmalar bilimsel ara ştırmalar de ğildir Acil’de İstatistik Sa ğlık istatistikleri sa ğlık çal ış anlar ının verdi ği bilgilerden derlenmekte Acil Servis’in hasta yo ğunlu ğunun y ıl-ay-gün-saat baz ında de ğerlendirilmesi bu veriler bir ülkede sa ğlık hizmetlerinin planlanmas ı Çal ış ma saatlerinin ve çal ış mas ı gereken ki şi say ısının ve de ğerlendirmesinde kullan ılmakta planlanmas ı Gerekli malzeme, yatak say ısı, ilaç vb. planlanmas ı Verilen hizmetin kalitesinin ölçülmesi İyi bir biyoistatistik eğitim alan sa ğlık personelinin o Eğitimin kalitesinin ölçülmesi ülkenin sa ğlık informasyon sistemlerine güvenilir Pandemi ve epidemilerin tespiti katk ılarda bulunmas ı beklenir Yeni çal ış malar, tezler … İstatistik Yaz ılım Programlar ı İİİstatistiksel -

Generalizability Theory in R
Practical Assessment, Research, and Evaluation Volume 24 Volume 24, 2019 Article 5 2019 Generalizability Theory in R Alan Huebner Marisa Lucht Follow this and additional works at: https://scholarworks.umass.edu/pare Recommended Citation Huebner, Alan and Lucht, Marisa (2019) "Generalizability Theory in R," Practical Assessment, Research, and Evaluation: Vol. 24 , Article 5. DOI: https://doi.org/10.7275/5065-gc10 Available at: https://scholarworks.umass.edu/pare/vol24/iss1/5 This Article is brought to you for free and open access by ScholarWorks@UMass Amherst. It has been accepted for inclusion in Practical Assessment, Research, and Evaluation by an authorized editor of ScholarWorks@UMass Amherst. For more information, please contact [email protected]. Huebner and Lucht: Generalizability Theory in R A peer-reviewed electronic journal. Copyright is retained by the first or sole author, who grants right of first publication to Practical Assessment, Research & Evaluation. Permission is granted to distribute this article for nonprofit, educational purposes if it is copied in its entirety and the journal is credited. PARE has the right to authorize third party reproduction of this article in print, electronic and database forms. Volume 24 Number 5, July 2019 ISSN 1531-7714 Generalizability Theory in R Alan Huebner and Marisa Lucht, University of Notre Dame Generalizability theory is a modern, powerful, and broad framework used to assess the reliability, or dependability, of measurements. While there exist classic works that explain the basic concepts and mathematical foundations of the method, there is currently a lack of resources addressing computational resources for those researchers wishing to apply generalizability in practice. -

Introduction to Astrostatistics and R
Introduction to Astrostatistics and R Eric Feigelson Penn State University Cosmology on the Beach, 2014 Lecture #1 My credentials Professor of Astronomy & Astrophysics and of Statistics Assoc Director, Center for Astrostatistics at Penn State Scientific Editor (methodology), Astrophysical Journal Chair, IAU Working Group in Astrostatistics & Astroinformatics Councils, Intl Astrostatistics Assn, AAS/WGAA, LSST/ISSC Lead author, MSMA textbook (2012 PROSE Award) Lead editor, Astrostatistics & Astroinformatics Portal Observational astronomer on small-scale structure at z<0.000001 Outline Introduction to astrostatistics – Role of statistics in astronomy – History of astrostatistics – Status of astrostatistics today Introduction to R – History of statistical computing – The R language & CRAN packages – Sample R script What is astronomy? Astronomy is the observational study of matter beyond Earth: planets in the Solar System, stars in the Milky Way Galaxy, galaxies in the Universe, and diffuse matter between these concentrations. Astrophysics is the study of the intrinsic nature of astronomical bodies and the processes by which they interact and evolve. This is an indirect, inferential intellectual effort based on the assumption that physics – gravity, electromagnetism, quantum mechanics, etc – apply universally to distant cosmic phenomena. What is statistics? (No consensus !!) Statistics characterizes and generalizes data – “… briefly, and in its most concrete form, the object of statistical methods is the reduction of data” (R. A. Fisher, 1922) -

Industrial Boilers & Pressure Vessels World Report
Industrial Boilers & Pressure Vessels World Report established in 1974, and a brand since 1981. www.datagroup.org Industrial Boilers & Pressure Vessels World Report Database Ref: M05014_M This database is updated monthly. Industrial Boilers & Pressure Vessels World Report INDUSTRIAL BOILERS WORLD REPORT The Industrial Boilers and Pressure Vessels Report has the following information. The base report has 59 chapters, plus the Excel spreadsheets & Access databases specified. This research provides World Data on Industrial Boilers and Pressure Vessels. The report is available in several Editions and Parts and the contents and cost of each part is shown below. The Client can choose the Edition required; and subsequently any Parts that are required from the After-Sales Service. Contents Description ....................................................................................................................................... 5 REPORT EDITIONS ........................................................................................................................... 6 World Report ....................................................................................................................................... 6 Regional Report ................................................................................................................................... 6 Country Report .................................................................................................................................... 6 Town & Country Report ...................................................................................................................... -
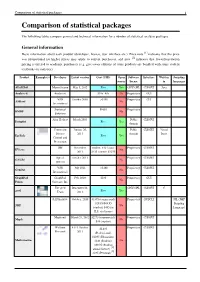
Comparison of Statistical Packages 1 Comparison of Statistical Packages
Comparison of statistical packages 1 Comparison of statistical packages The following tables compare general and technical information for a number of statistical analysis packages. General information Basic information about each product (developer, license, user interface etc.). Price note [1] indicates that the price was promotional (so higher prices may apply to current purchases), and note [2] indicates that lower/penetration pricing is offered to academic purchasers (e.g. give-away editions of some products are bundled with some student textbooks on statistics). Product Example(s) Developer Latest version Cost (USD) Open Software Interface Written Scripting source license in languages ADaMSoft Marco Scarno May 5, 2012 Free Yes GNU GPL CLI/GUI Java Analyse-it Analyse-it $185–495 No Proprietary GUI VSN October 2009 >$150 Proprietary CLI ASReml No International Statistical $1095 Proprietary BMDP No Solutions Alan Heckert March 2005 Public CLI/GUI Dataplot Free Yes domain Centers for January 26, Public CLI/GUI Visual Disease 2011 domain Basic Epi Info Free Yes Control and Prevention IHS November student: $40 / acad: Proprietary CLI/GUI EViews No 2011 $425 / comm: $1075 Aptech October 2011 Proprietary CLI/GUI GAUSS No systems VSN July 2011 >$190 Proprietary CLI/GUI GenStat No International GraphPad GraphPad Feb. 2009 $595 Proprietary GUI No Prism Software, Inc. The gretl December 22, GNU GPL CLI/GUI C gretl Team 2011 Free Yes SAS Institute October, 2010 $1895 (commercial) Proprietary GUI/CLI JSL (JMP $29.95/$49.95 Scripting JMP No (student) $495 for Language) H.S. site licence Maplesoft March 28, 2012 $2275 (commercial), Proprietary CLI/GUI Maple No $99 (student) Wolfram 8.0.4, October $2,495 Proprietary CLI/GUI Research 2011 (Professional), $1095 (Education), Mathematica $140 (Student), No $69.95 (Student [3] annual license) [4] $295 (Personal) Comparison of statistical packages 2 The New releases Depends on many Proprietary CLI/GUI Java MATLAB No MathWorks twice per year things. -

Years of Data Science
JOURNAL OF COMPUTATIONAL AND GRAPHICAL STATISTICS , VOL. , NO. , – https://doi.org/./.. Years of Data Science David Donoho Department of Statistics, Stanford University, Standford, CA ABSTRACT ARTICLE HISTORY More than 50 years ago, John Tukey called for a reformation of academic statistics. In “The Future of Data science Received August Analysis,” he pointed to the existence of an as-yet unrecognized , whose subject of interest was Revised August learning from data, or “data analysis.” Ten to 20 years ago, John Chambers, Jeff Wu, Bill Cleveland, and Leo Breiman independently once again urged academic statistics to expand its boundaries beyond the KEYWORDS classical domain of theoretical statistics; Chambers called for more emphasis on data preparation and Cross-study analysis; Data presentation rather than statistical modeling; and Breiman called for emphasis on prediction rather than analysis; Data science; Meta inference. Cleveland and Wu even suggested the catchy name “data science” for this envisioned field. A analysis; Predictive modeling; Quantitative recent and growing phenomenon has been the emergence of “data science”programs at major universities, programming environments; including UC Berkeley, NYU, MIT, and most prominently, the University of Michigan, which in September Statistics 2015 announced a $100M “Data Science Initiative” that aims to hire 35 new faculty. Teaching in these new programs has significant overlap in curricular subject matter with traditional statistics courses; yet many aca- demic statisticians perceive the new programs as “cultural appropriation.”This article reviews some ingredi- ents of the current “data science moment,”including recent commentary about data science in the popular media, and about how/whether data science is really different from statistics.