Quadtree Based JBIG Compression
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Microsoft Office Open XML Formats New File Formats for “Office 12”
The Microsoft Office Open XML Formats New File Formats for “Office 12” White Paper Published: June 2005 For the latest information, please see http://www.microsoft.com/office/wave12 Contents Introduction ...............................................................................................................................1 From .doc to .docx: a brief history of the Office file formats.................................................1 Benefits of the Microsoft Office Open XML Formats ................................................................2 Integration with Business Data .............................................................................................2 Openness and Transparency ...............................................................................................4 Robustness...........................................................................................................................7 Description of the Microsoft Office Open XML Format .............................................................9 Document Parts....................................................................................................................9 Microsoft Office Open XML Format specifications ...............................................................9 Compatibility with new file formats........................................................................................9 For more information ..............................................................................................................10 -

Why ODF?” - the Importance of Opendocument Format for Governments
“Why ODF?” - The Importance of OpenDocument Format for Governments Documents are the life blood of modern governments and their citizens. Governments use documents to capture knowledge, store critical information, coordinate activities, measure results, and communicate across departments and with businesses and citizens. Increasingly documents are moving from paper to electronic form. To adapt to ever-changing technology and business processes, governments need assurance that they can access, retrieve and use critical records, now and in the future. OpenDocument Format (ODF) addresses these issues by standardizing file formats to give governments true control over their documents. Governments using applications that support ODF gain increased efficiencies, more flexibility and greater technology choice, leading to enhanced capability to communicate with and serve the public. ODF is the ISO Approved International Open Standard for File Formats ODF is the only open standard for office applications, and it is completely vendor neutral. Developed through a transparent, multi-vendor/multi-stakeholder process at OASIS (Organization for the Advancement of Structured Information Standards), it is an open, XML- based document file format for displaying, storing and editing office documents, such as spreadsheets, charts, and presentations. It is available for implementation and use free from any licensing, royalty payments, or other restrictions. In May 2006, it was approved unanimously as an International Organization for Standardization (ISO) and International Electrotechnical Commission (IEC) standard. Governments and Businesses are Embracing ODF The promotion and usage of ODF is growing rapidly, demonstrating the global need for control and choice in document applications. For example, many enlightened governments across the globe are making policy decisions to move to ODF. -

MPEG-21 Overview
MPEG-21 Overview Xin Wang Dept. Computer Science, University of Southern California Workshop on New Multimedia Technologies and Applications, Xi’An, China October 31, 2009 Agenda ● What is MPEG-21 ● MPEG-21 Standards ● Benefits ● An Example Page 2 Workshop on New Multimedia Technologies and Applications, Oct. 2009, Xin Wang MPEG Standards ● MPEG develops standards for digital representation of audio and visual information ● So far ● MPEG-1: low resolution video/stereo audio ● E.g., Video CD (VCD) and Personal music use (MP3) ● MPEG-2: digital television/multichannel audio ● E.g., Digital recording (DVD) ● MPEG-4: generic video and audio coding ● E.g., MP4, AVC (H.24) ● MPEG-7 : visual, audio and multimedia descriptors MPEG-21: multimedia framework ● MPEG-A: multimedia application format ● MPEG-B, -C, -D: systems, video and audio standards ● MPEG-M: Multimedia Extensible Middleware ● ● MPEG-V: virtual worlds MPEG-U: UI ● (29116): Supplemental Media Technologies ● ● (Much) more to come … Page 3 Workshop on New Multimedia Technologies and Applications, Oct. 2009, Xin Wang What is MPEG-21? ● An open framework for multimedia delivery and consumption ● History: conceived in 1999, first few parts ready early 2002, most parts done by now, some amendment and profiling works ongoing ● Purpose: enable all-electronic creation, trade, delivery, and consumption of digital multimedia content ● Goals: ● “Transparent” usage ● Interoperable systems ● Provides normative methods for: ● Content identification and description Rights management and protection ● Adaptation of content ● Processing on and for the various elements of the content ● ● Evaluation methods for determining the appropriateness of possible persistent association of information ● etc. Page 4 Workshop on New Multimedia Technologies and Applications, Oct. -

Free Lossless Image Format
FREE LOSSLESS IMAGE FORMAT Jon Sneyers and Pieter Wuille [email protected] [email protected] Cloudinary Blockstream ICIP 2016, September 26th DON’T WE HAVE ENOUGH IMAGE FORMATS ALREADY? • JPEG, PNG, GIF, WebP, JPEG 2000, JPEG XR, JPEG-LS, JBIG(2), APNG, MNG, BPG, TIFF, BMP, TGA, PCX, PBM/PGM/PPM, PAM, … • Obligatory XKCD comic: YES, BUT… • There are many kinds of images: photographs, medical images, diagrams, plots, maps, line art, paintings, comics, logos, game graphics, textures, rendered scenes, scanned documents, screenshots, … EVERYTHING SUCKS AT SOMETHING • None of the existing formats works well on all kinds of images. • JPEG / JP2 / JXR is great for photographs, but… • PNG / GIF is great for line art, but… • WebP: basically two totally different formats • Lossy WebP: somewhat better than (moz)JPEG • Lossless WebP: somewhat better than PNG • They are both .webp, but you still have to pick the format GOAL: ONE FORMAT THAT COMPRESSES ALL IMAGES WELL EXPERIMENTAL RESULTS Corpus Lossless formats JPEG* (bit depth) FLIF FLIF* WebP BPG PNG PNG* JP2* JXR JLS 100% 90% interlaced PNGs, we used OptiPNG [21]. For BPG we used [4] 8 1.002 1.000 1.234 1.318 1.480 2.108 1.253 1.676 1.242 1.054 0.302 the options -m 9 -e jctvc; for WebP we used -m 6 -q [4] 16 1.017 1.000 / / 1.414 1.502 1.012 2.011 1.111 / / 100. For the other formats we used default lossless options. [5] 8 1.032 1.000 1.099 1.163 1.429 1.664 1.097 1.248 1.500 1.017 0.302� [6] 8 1.003 1.000 1.040 1.081 1.282 1.441 1.074 1.168 1.225 0.980 0.263 Figure 4 shows the results; see [22] for more details. -

OASIS CGM Open Webcgm V2.1
WebCGM Version 2.1 OASIS Standard 01 March 2010 Specification URIs: This Version: XHTML multi-file: http://docs.oasis-open.org/webcgm/v2.1/os/webcgm-v2.1-index.html (AUTHORITATIVE) PDF: http://docs.oasis-open.org/webcgm/v2.1/os/webcgm-v2.1.pdf XHTML ZIP archive: http://docs.oasis-open.org/webcgm/v2.1/os/webcgm-v2.1.zip Previous Version: XHTML multi-file: http://docs.oasis-open.org/webcgm/v2.1/cs02/webcgm-v2.1-index.html (AUTHORITATIVE) PDF: http://docs.oasis-open.org/webcgm/v2.1/cs02/webcgm-v2.1.pdf XHTML ZIP archive: http://docs.oasis-open.org/webcgm/v2.1/cs02/webcgm-v2.1.zip Latest Version: XHTML multi-file: http://docs.oasis-open.org/webcgm/v2.1/latest/webcgm-v2.1-index.html PDF: http://docs.oasis-open.org/webcgm/v2.1/latest/webcgm-v2.1.pdf XHTML ZIP archive: http://docs.oasis-open.org/webcgm/v2.1/latest/webcgm-v2.1.zip Declared XML namespaces: http://www.cgmopen.org/schema/webcgm/ System Identifier: http://docs.oasis-open.org/webcgm/v2.1/webcgm21.dtd Technical Committee: OASIS CGM Open WebCGM TC Chair(s): Stuart Galt, The Boeing Company Editor(s): Benoit Bezaire, PTC Lofton Henderson, Individual Related Work: This specification updates: WebCGM 2.0 OASIS Standard (and W3C Recommendation) This specification, when completed, will be identical in technical content to: WebCGM 2.1 W3C Recommendation, available at http://www.w3.org/TR/webcgm21/. Abstract: Computer Graphics Metafile (CGM) is an ISO standard, defined by ISO/IEC 8632:1999, for the interchange of 2D vector and mixed vector/raster graphics. -
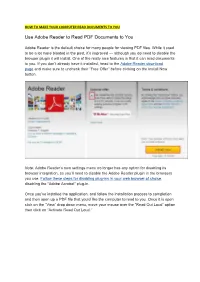
Use Adobe Reader to Read PDF Documents to You
HOW TO MAKE YOUR COMPUTER READ DOCUMENTS TO YOU Use Adobe Reader to Read PDF Documents to You Adobe Reader is the default choice for many people for viewing PDF files. While it used to be a lot more bloated in the past, it’s improved — although you do need to disable the browser plugin it will install. One of the really nice features is that it can read documents to you. If you don’t already have it installed, head to the Adobe Reader download page and make sure to uncheck their “Free Offer” before clicking on the Install Now button. Note: Adobe Reader’s own settings menu no longer has any option for disabling its browser integration, so you’ll need to disable the Adobe Reader plugin in the browsers you use. Follow these steps for disabling plug-ins in your web browser of choice, disabling the “Adobe Acrobat” plug-in. Once you’ve installed the application, and follow the installation process to completion and then open up a PDF file that you’d like the computer to read to you. Once it is open click on the “View” drop down menu, move your mouse over the “Read Out Loud” option then click on “Activate Read Out Loud.” Alternatively, you can click “Ctrl,” “Shift,” and “Y” (Ctrl+Shift+Y) on your keyboard to activate the feature. Once the feature is activated, you can click on a single paragraph to make windows read it back to you. Another option would be to navigate to the “View” menu, then “Read Out Loud” and select an option that fits your needs as shown in the Image below. -

MPEG Compression Is Based on Processing 8 X 8 Pixel Blocks
MPEG-1 & MPEG-2 Compression 6th of March, 2002, Mauri Kangas Contents: • MPEG Background • MPEG-1 Standard (shortly) • MPEG-2 Standard (shortly) • MPEG-1 and MPEG-2 Differencies • MPEG Encoding and Decoding • Colour sub-sampling • Motion Compensation • Slices, macroblocks, blocks, etc. • DCT • MPEG-2 bit stream syntax • MPEG-2 • Supported Features • Levels • Profiles • DVB Systems 1 © Mauri Kangas 2002 MPEG-1,2.PPT/ 24.02.2002 / Mauri Kangas MPEG Background • MPEG = Motion Picture Expert Group • ISO/IEC JTC1/SC29 • WG11 Motion Picture Experts Group (MPEG) • WG10 Joint Photographic Experts Group (JPEG) • WG7 Computer Graphics Experts Group (CGEG) • WG9 Joint Bi-level Image coding experts Group (JBIG) • WG12 Multimedia and Hypermedia information coding Experts Group (MHEG) • MPEG-1,2 Standardization 1988- • Requirement • System • Video • Audio • Implementation • Testing • Latest MPEG Standardization: MPEG-4, MPEG-7, MPEG-21 2 © Mauri Kangas 2002 MPEG-1,2.PPT/ 24.02.2002 / Mauri Kangas MPEG-1 Standard ISO/IEC 11172-2 (1991) "Coding of moving pictures and associated audio for digital storage media" Video • optimized for bitrates around 1.5 Mbit/s • originally optimized for SIF picture format, but not limited to it: • 352x240 pixels a 30 frames/sec [ NTSC based ] • 352x288 pixels at 25 frames/sec [ PAL based ] • progressive frames only - no direct provision for interlaced video applications, such as broadcast television Audio • joint stereo audio coding at 192 kbit/s (layer 2) System • mainly designed for error-free digital storage media • -

Iso/Iec 14496-14
INTERNATIONAL ISO/IEC STANDARD 14496-14 First edition 2003-11-15 Information technology — Coding of audio-visual objects — Part 14: MP4 file format Technologies de l'information — Codage des objets audiovisuels — Partie 14: Format de fichier MP4 Reference number ISO/IEC 14496-14:2003(E) Licensed to WIMOBILIS DIGITAL TECHNOLOGIES/MARCOS MANENTE ISO Store order #:850777/Downloaded:2007-09-27 Single user licence only, copying and networking prohibited © ISO/IEC 2003 ISO/IEC 14496-14:2003(E) PDF disclaimer This PDF file may contain embedded typefaces. In accordance with Adobe's licensing policy, this file may be printed or viewed but shall not be edited unless the typefaces which are embedded are licensed to and installed on the computer performing the editing. In downloading this file, parties accept therein the responsibility of not infringing Adobe's licensing policy. The ISO Central Secretariat accepts no liability in this area. Adobe is a trademark of Adobe Systems Incorporated. Details of the software products used to create this PDF file can be found in the General Info relative to the file; the PDF-creation parameters were optimized for printing. Every care has been taken to ensure that the file is suitable for use by ISO member bodies. In the unlikely event that a problem relating to it is found, please inform the Central Secretariat at the address given below. © ISO/IEC 2003 All rights reserved. Unless otherwise specified, no part of this publication may be reproduced or utilized in any form or by any means, electronic or mechanical, including photocopying and microfilm, without permission in writing from either ISO at the address below or ISO's member body in the country of the requester. -
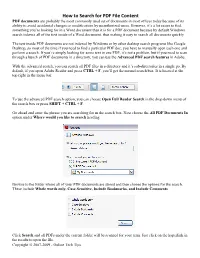
How to Search for PDF File Content
How to Search for PDF File Content PDF documents are probably the most commonly used set of documents in most offices today because of its ability to avoid accidental changes or modifications by unauthorized users. However, it’s a lot easier to find something you’re looking for in a Word document than it is for a PDF document because by default Windows search indexes all of the text inside of a Word document, thus making it easy to search all documents quickly. The text inside PDF documents are not indexed by Windows or by other desktop search programs like Google Desktop, so most of the time if you need to find a particular PDF doc, you have to manually open each one and perform a search. If you’re simply looking for some text in one PDF, it’s not a problem, but if you need to scan through a bunch of PDF documents in a directory, you can use the Advanced PDF search features in Adobe. With the advanced search, you can search all PDF files in a directory and it’s sub-directories in a single go. By default, if you open Adobe Reader and press CTRL + F, you’ll get the normal search box. It is located at the top right in the menu bar. To use the advanced PDF search option, you can choose Open Full Reader Search in the drop down menu of the search box or press SHIFT + CTRL + F. Go ahead and enter the phrase you are searching for in the search box. -
![CISC 3635 [36] Multimedia Coding and Compression](https://docslib.b-cdn.net/cover/4741/cisc-3635-36-multimedia-coding-and-compression-814741.webp)
CISC 3635 [36] Multimedia Coding and Compression
Brooklyn College Department of Computer and Information Sciences CISC 3635 [36] Multimedia Coding and Compression 3 hours lecture; 3 credits Media types and their representation. Multimedia coding and compression. Lossless data compression. Lossy data compression. Compression standards: text, audio, image, fax, and video. Course Outline: 1. Media Types and Their Representations (Week 1-2) a. Text b. Analog and Digital Audio c. Digitization of Sound d. Musical Instrument Digital Interface (MIDI) e. Audio Coding: Pulse Code Modulation (PCM) f. Graphics and Images Data Representation g. Image File Formats: GIF, JPEG, PNG, TIFF, BMP, etc. h. Color Science and Models i. Fax j. Video Concepts k. Video Signals: Component, Composite, S-Video l. Analog and Digital Video: NTSC, PAL, SECAM, HDTV 2. Lossless Compression Algorithms (Week 3-4) a. Basics of Information Theory b. Run-Length Coding c. Variable Length Coding: Huffman Coding d. Basic Fax Compression e. Dictionary Based Coding: LZW Compression f. Arithmetic Coding g. Lossless Image Compression 3. Lossy Compression Algorithms (Week 5-6) a. Distortion Measures b. Quantization c. Transform Coding d. Wavelet Based Coding e. Embedded Zerotree of Wavelet (EZW) Coefficients 4. Basic Audio Compression (Week 7-8) a. Differential Coders: DPCM, ADPCM, DM b. Vocoders c. Linear Predictive Coding (LPC) d. CELP e. Audio Standards: G.711, G.726, G.723, G.728. G.729, etc. 5. Image Compression Standards (Week 9) a. The JPEG Standard b. JPEG 2000 c. JPEG-LS d. Bilevel Image Compression Standards: JBIG, JBIG2 6. Basic Video Compression (Week 10) a. Video Compression Based on Motion Compensation b. Search for Motion Vectors c. -
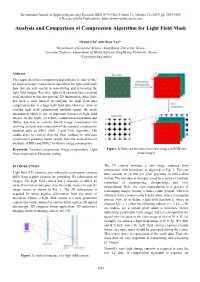
Analysis and Comparison of Compression Algorithm for Light Field Mask
International Journal of Applied Engineering Research ISSN 0973-4562 Volume 12, Number 12 (2017) pp. 3553-3556 © Research India Publications. http://www.ripublication.com Analysis and Comparison of Compression Algorithm for Light Field Mask Hyunji Cho1 and Hoon Yoo2* 1Department of Computer Science, SangMyung University, Korea. 2Associate Professor, Department of Media Software SangMyung University, Korea. *Corresponding author Abstract This paper describes comparison and analysis of state-of-the- art lossless image compression algorithms for light field mask data that are very useful in transmitting and refocusing the light field images. Recently, light field cameras have received wide attention in that they provide 3D information. Also, there has been a wide interest in studying the light field data compression due to a huge light field data. However, most of existing light field compression methods ignore the mask information which is one of important features of light field images. In this paper, we reports compression algorithms and further use this to achieve binary image compression by realizing analysis and comparison of the standard compression methods such as JBIG, JBIG 2 and PNG algorithm. The results seem to confirm that the PNG method for text data compression provides better results than the state-of-the-art methods of JBIG and JBIG2 for binary image compression. Keywords: Lossless compression, Image compression, Light Figure. 2. Basic architecture from raw images to RGB and filed compression, Plenoptic coding mask images INTRODUCTION The LF camera provides a raw image captured from photosensor with microlens, as depicted in Fig. 1. The raw Light field (LF) cameras, also referred to as plenoptic cameras, data consists of 10 bits per pixel precision in little-endian differ from regular cameras by providing 3D information of format. -

CGM Whitepaper
Table of Contents _________________________________________________ Background ______________________________________________________ 1 The Case for a CGM Archive _________________________________________ 3 OPEN STANDARD _______________________________________________________ 3 STANDARDS BASED _____________________________________________________ 3 INTEROPERABILITY _____________________________________________________ 4 INTELLIGENT GRAPHICS _________________________________________________ 4 SINGLE SOURCE PUBLISHING _____________________________________________ 4 Challenges when creating a CGM Archive _______________________________ 5 SOURCES OF GRAPHICAL INFORMATION _____________________________________ 5 QUANTITY OF DATA _____________________________________________________ 5 GRAPHICS QUALITY _____________________________________________________ 5 TECHNOLOGY __________________________________________________________ 6 COST AND RETURN ON INVESTMENT ________________________________________ 6 Optimize the technical graphics process using Larson CGM Products __________ 7 CORE BENEFITS ________________________________________________________ 7 The Benefits of the Larson CGM Products ___________________________________ 8 Features of the Larson CGM Products __________________________________ 9 VIZEX TRANSFORM______________________________________________________ 9 Transform DWG and DXF files ____________________________________________ 9 Transform PDF files ___________________________________________________ 10 Transform Image files _________________________________________________