A Non Linear Approach Towards Automated Emotion Analysis in Hindustani Music
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1 Syllabus for MA (Previous) Hindustani Music Vocal/Instrumental
Syllabus for M.A. (Previous) Hindustani Music Vocal/Instrumental (Sitar, Sarod, Guitar, Violin, Santoor) SEMESTER-I Core Course – 1 Theory Credit - 4 Theory : 70 Internal Assessment : 30 Maximum Marks : 100 Historical and Theoretical Study of Ragas 70 Marks A. Historical Study of the following Ragas from the period of Sangeet Ratnakar onwards to modern times i) Gaul/Gaud iv) Kanhada ii) Bhairav v) Malhar iii) Bilawal vi) Todi B. Development of Raga Classification system in Ancient, Medieval and Modern times. C. Study of the following Ragangas in the modern context:- Sarang, Malhar, Kanhada, Bhairav, Bilawal, Kalyan, Todi. D. Detailed and comparative study of the Ragas prescribed in Appendix – I Internal Assessment 30 marks Core Course – 2 Theory Credit - 4 Theory : 70 Internal Assessment : 30 Maximum Marks : 100 Music of the Asian Continent 70 Marks A. Study of the Music of the following - China, Arabia, Persia, South East Asia, with special reference to: i) Origin, development and historical background of Music ii) Musical scales iii) Important Musical Instruments B. A comparative study of the music systems mentioned above with Indian Music. Internal Assessment 30 marks Core Course – 3 Practical Credit - 8 Practical : 70 Internal Assessment : 30 Maximum Marks : 100 Stage Performance 70 marks Performance of half an hour’s duration before an audience in Ragas selected from the list of Ragas prescribed in Appendix – I Candidate may plan his/her performance in the following manner:- Classical Vocal Music i) Khyal - Bada & chota Khyal with elaborations for Vocal Music. Tarana is optional. Classical Instrumental Music ii) Alap, Jor, Jhala, Masitkhani and Razakhani Gat with eleaborations Semi Classical Music iii) A short piece of classical music /Thumri / Bhajan/ Dhun /a gat in a tala other than teentaal may also be presented. -

Famous Indian Classical Musicians and Vocalists Free Static GK E-Book
oliveboard FREE eBooks FAMOUS INDIAN CLASSICAL MUSICIANS & VOCALISTS For All Banking and Government Exams Famous Indian Classical Musicians and Vocalists Free static GK e-book Current Affairs and General Awareness section is one of the most important and high scoring sections of any competitive exam like SBI PO, SSC-CGL, IBPS Clerk, IBPS SO, etc. Therefore, we regularly provide you with Free Static GK and Current Affairs related E-books for your preparation. In this section, questions related to Famous Indian Classical Musicians and Vocalists have been asked. Hence it becomes very important for all the candidates to be aware about all the Famous Indian Classical Musicians and Vocalists. In all the Bank and Government exams, every mark counts and even 1 mark can be the difference between success and failure. Therefore, to help you get these important marks we have created a Free E-book on Famous Indian Classical Musicians and Vocalists. The list of all the Famous Indian Classical Musicians and Vocalists is given in the following pages of this Free E-book on Famous Indian Classical Musicians and Vocalists. Sample Questions - Q. Ustad Allah Rakha played which of the following Musical Instrument? (a) Sitar (b) Sarod (c) Surbahar (d) Tabla Answer: Option D – Tabla Q. L. Subramaniam is famous for playing _________. (a) Saxophone (b) Violin (c) Mridangam (d) Flute Answer: Option B – Violin Famous Indian Classical Musicians and Vocalists Free static GK e-book Famous Indian Classical Musicians and Vocalists. Name Instrument Music Style Hindustani -
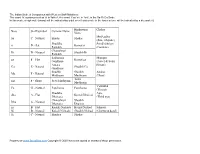
Note Staff Symbol Carnatic Name Hindustani Name Chakra Sa C
The Indian Scale & Comparison with Western Staff Notations: The vowel 'a' is pronounced as 'a' in 'father', the vowel 'i' as 'ee' in 'feet', in the Sa-Ri-Ga Scale In this scale, a high note (swara) will be indicated by a dot over it and a note in the lower octave will be indicated by a dot under it. Hindustani Chakra Note Staff Symbol Carnatic Name Name MulAadhar Sa C - Natural Shadaj Shadaj (Base of spine) Shuddha Swadhishthan ri D - flat Komal ri Rishabh (Genitals) Chatushruti Ri D - Natural Shudhh Ri Rishabh Sadharana Manipur ga E - Flat Komal ga Gandhara (Navel & Solar Antara Plexus) Ga E - Natural Shudhh Ga Gandhara Shudhh Shudhh Anahat Ma F - Natural Madhyam Madhyam (Heart) Tivra ma F - Sharp Prati Madhyam Madhyam Vishudhh Pa G - Natural Panchama Panchama (Throat) Shuddha Ajna dha A - Flat Komal Dhaivat Dhaivata (Third eye) Chatushruti Shudhh Dha A - Natural Dhaivata Dhaivat ni B - Flat Kaisiki Nishada Komal Nishad Sahsaar Ni B - Natural Kakali Nishada Shudhh Nishad (Crown of head) Så C - Natural Shadaja Shadaj Property of www.SarodSitar.com Copyright © 2010 Not to be copied or shared without permission. Short description of Few Popular Raags :: Sanskrut (Sanskrit) pronunciation is Raag and NOT Raga (Alphabetical) Aroha Timing Name of Raag (Karnataki Details Avroha Resemblance) Mood Vadi, Samvadi (Main Swaras) It is a old raag obtained by the combination of two raags, Ahiri Sa ri Ga Ma Pa Ga Ma Dha ni Så Ahir Bhairav Morning & Bhairav. It belongs to the Bhairav Thaat. Its first part (poorvang) has the Bhairav ang and the second part has kafi or Så ni Dha Pa Ma Ga ri Sa (Chakravaka) serious, devotional harpriya ang. -

Categorization of Stringed Instruments with Multifractal Detrended Fluctuation Analysis
CATEGORIZATION OF STRINGED INSTRUMENTS WITH MULTIFRACTAL DETRENDED FLUCTUATION ANALYSIS Archi Banerjee*, Shankha Sanyal, Tarit Guhathakurata, Ranjan Sengupta and Dipak Ghosh Sir C.V. Raman Centre for Physics and Music Jadavpur University, Kolkata: 700032 *[email protected] * Corresponding Author ABSTRACT Categorization is crucial for content description in archiving of music signals. On many occasions, human brain fails to classify the instruments properly just by listening to their sounds which is evident from the human response data collected during our experiment. Some previous attempts to categorize several musical instruments using various linear analysis methods required a number of parameters to be determined. In this work, we attempted to categorize a number of string instruments according to their mode of playing using latest-state-of-the-art robust non-linear methods. For this, 30 second sound signals of 26 different string instruments from all over the world were analyzed with the help of non linear multifractal analysis (MFDFA) technique. The spectral width obtained from the MFDFA method gives an estimate of the complexity of the signal. From the variation of spectral width, we observed distinct clustering among the string instruments according to their mode of playing. Also there is an indication that similarity in the structural configuration of the instruments is playing a major role in the clustering of their spectral width. The observations and implications are discussed in detail. Keywords: String Instruments, Categorization, Fractal Analysis, MFDFA, Spectral Width INTRODUCTION Classification is one of the processes involved in audio content description. Audio signals can be classified according to miscellaneous criteria viz. speech, music, sound effects (or noises). -

Hindustani Classic Music
HINDUSTANI CLASSIC MUSIC: Junior Grade or Prathamik : Syllabus : No theory exam in this grade Swarajnana Talajnana essential Ragajnana Practicals: 1. Beginning of swarabyasa - in three layas 2. 2 Swaramalikas 5 Lakshnageete Chotakyal Alap - 4 ragas Than - 4 Drupad - should be practiced 3. Bhajan - Vachana - Dasapadas 4. Theental, Dadara, Ektal (Dhruth), Chontal, Juptal, Kheruva Talu - Sam-Pet-Husi-Matras - should practice Tekav. 5. Swarajnana 6. Knowledge of the words - nada, shruthi, Aroha, Avaroha, Vadi - Samvedi, Komal - Theevra - Shuddha - Sasthak - Ganasamay - Thaat - Varjya. 7. Swaralipi - should be learnt. Senior Grade: (Madhyamik) Syllabus : Theory: 1. Paribhashika words 2. Sound & place of emergence of sound 3. The practice of different ragas out of “thaat” - based on Pandith Venkatamukhi Mela System 4. To practice ragalaskhanas of different ragas 5. Different Talas - 9 (Trital, Dadra, Jup, Kherva, Chantal, Tilawad, Roopak, Damar, Deepchandi) explanation of talas with Tekas. 6. Chotakhyal, Badakhyal, Bhajan, Tumari, Geethprakaras - Lakshanas. 7. Life history of Jayadev, Sarangdev, Surdas, Purandaradas, Tansen, Akkamahadevi, Sadarang, Kabeer, Meera, Haridas. 8. Knowledge of musical instrument Practicals: 1. Among 20 ragas - Chotakhyal in each 2. Badakhyal - for 10 ragas (Bhoopali, Yamani, Bheempalas, Bageshree, Malkonnse, Alhaiah Bilawal, Bahar, Kedar, Poorvi, Shankara. 3. Learn to sing one drupad in Tay, Dugun & Changun - one Damargeete. VIDHWAN PROFICIENCY Syllabus: Theory 1. Paribhashika Shabdas. 2. 7 types of Talas - their parts (angas) 3. Tabala bol - Tala Jnana, Vilambitha Ektal, Jumra, Adachontal, Savari, Panjabi, Tappa. 4. Raga lakshanas of Bhairav, Shuddha Sarang, Peelu, Multhani, Sindura, Adanna, Jogiya, Hamsadhwani, Gandamalhara, Ragashree, Darbari, Kannada, Basanthi, Ahirbhairav, Todi etc., Alap, Swaravisthara, Sama Prakruthi, Ragas criticism, Gana samay - should be known. -

The Asian Indian Classical Music Society Vishwa Mohan Bhatt
The Asian Indian Classical Music Society 52318 N Tally Ho Drive, South Bend, IN 46635 March 28 , 2013 Dear Friends, I am writing to inform you about our concerts for Spring 2013: Vishwa Mohan Bhatt (Mohan Veena or Guitar) with Subhen Chatterjee (Tabla) April 10th , 2013, Wedneday,7.00 PM, at the Hesburgh Center Auditorium Pandit Vishwa Mohan Bhatt is among the leading Indian classical instrumental musicians. He is the creator of the Mohan Veena, which has modified the Hawaiian slide guitar by adding fourteen additional strings to it, and allows him to exquisitely assimilate the techniques of the sitar, sarod and veena. He is one of the foremost disciples of Pandit Ravi Shankar. He has captivated audiences at numerous concerts in the US, Canada, Europe, the Middle East and, of course, India. Among numerous other awards, he is the recipient of the Grammy Award, 1994, with Ry Cooder, for the World Music album, A Meeting by the River. Shanmukha Priya and Hari Priya (Vocal) with M.A. Krishnaswamy (Violin) and Skandasubramanian (Mridangam), April 26th , 2013, Friday, 7.00PM, place: TBA Shanmukha Priya and Hari Priya, the renowned musical duo popularly known as the “Priya Sisters”, are among the leading exponents of the Carnatic or South Indian vocal music. After receiving their training from the renowned duo, Radha and Jayalakshmi, they are now under the guidance of Prof. T. R.Subramaniam. Since they began performing in 1989, the Priya Sisters have performed worldwide in more than two thousand concerts. Among other awards, the sisters have been the recipients of the 'Best Female Vocalists' awards from Music Academy, Sri Krishna Gana Sabha and the Indian Fine Arts Society, Chennai. -

A Novel EEG Based Study with Hindustani Classical Music
Can Musical Emotion Be Quantified With Neural Jitter Or Shimmer? A Novel EEG Based Study With Hindustani Classical Music Sayan Nag, Sayan Biswas, Sourya Sengupta Shankha Sanyal, Archi Banerjee, Ranjan Department of Electrical Engineering Sengupta,Dipak Ghosh Jadavpur University Sir C.V. Raman Centre for Physics and Music Kolkata, India Jadavpur University Kolkata, India Abstract—The term jitter and shimmer has long been used in In India, music (geet) has been a subject of aesthetic and the domain of speech and acoustic signal analysis as a parameter intellectual discourse since the times of Vedas (samaveda). for speaker identification and other prosodic features. In this Rasa was examined critically as an essential part of the theory study, we look forward to use the same parameters in neural domain to identify and categorize emotional cues in different of art by Bharata in Natya Sastra, (200 century BC). The rasa musical clips. For this, we chose two ragas of Hindustani music is considered as a state of enhanced emotional perception which are conventionally known to portray contrast emotions produced by the presence of musical energy. It is perceived as and EEG study was conducted on 5 participants who were made a sentiment, which could be described as an aesthetic to listen to 3 min clip of these two ragas with sufficient resting experience. Although unique, one can distinguish several period in between. The neural jitter and shimmer components flavors according to the emotion that colors it [11]. Several were evaluated for each experimental condition. The results reveal interesting information regarding domain specific arousal emotional flavors are listed, namely erotic love (sringara), of human brain in response to musical stimuli and also regarding pathetic (karuna), devotional (bhakti), comic (hasya), horrific trait characteristics of an individual. -

Music from the Beginning
Review Article iMedPub Journals 2015 Insights in Blood Pressure http://journals.imedpub.com Vol. 1 No. 1:2 ISSN 2471-9897 Music and its Effect on Body, Brain/Mind: Archi Banerjee, Shankha A Study on Indian Perspective by Neuro- Sanyal, Ranjan Sengupta, Dipak Ghosh physical Approach Sir CV Raman Centre for Physics and Music, Jadavpur University, Kolkata Keywords: Music Cognition, Music Therapy, Diabetes, Blood Pressure, Neurocognitive Benefits Corresponding author: Archi Banerjee Received: Sep 20, 2015, Accepted: Sep 22, 2015, Submitted:Sep 29, 2015 [email protected] Music from the Beginning Sir CV Raman Centre for Physics and Music, The singing of the birds, the sounds of the endless waves of the Jadavpur University, Kolkata 700032. sea, the magical sounds of drops of rain falling on a tin roof, the murmur of trees, songs, the beautiful sounds produced by Tel: +919038569341 strumming the strings of musical instruments–these are all music. Some are produced by nature while others are produced by man. Natural sounds existed before human beings appeared Citation: Banerjee A, Sanyal S, Sengupta R, on earth. Was it music then or was it just mere sounds? Without et al. Music and its Effect on Body, Brain/ an appreciative mind, these sounds are meaningless. So music Mind: A Study on Indian Perspective by has meaning and music needs a mind to appreciate it. Neuro-physical Approach. Insights Blood Press 2015, 1:1. Music therefore may be defined as a form of auditory communication between the producer and the receiver. There are other forms of auditory communication, like speech, but the past and Raman, Kar followed by Rossing and Sundberg later on, difference is that music is more universal and evokes emotion. -

J 1607 PAPER II.P65
Signature and Name of Invigilator Answer Sheet No. : ...................................................... (To be filled by the Candidate) 1. (Signature) Roll No. (Name) (In figures as per admission card) 2. (Signature) Roll No. (In words) (Name) Test Booklet No. J1 6 0 7 PAPERII Time : 1¼ hours]MUSIC [Maximum Marks : 100 Number of Pages in this Booklet : 48 Number of Questions in this Booklet : 50 Instructions for the Candidates ÂÚUèÿææçÍüØô¢ ·ð¤ çÜ° çÙÎðüàæ 1. Write your roll number in the space provided on the top of this 1. ÂãÜðU ÂëDU ·ð¤ ª¤ÂÚU çÙØÌ SÍæÙ ÂÚU ¥ÂÙæ ÚUôÜU ÙÕÚU çÜç¹°Ð page. 2. §â ÂýàÙ-Âæ ×𢠿æâ Õãéçß·¤ËÂèØ ÂýàÙ ãñ¢Ð 2. This paper consists of fifty multiple-choice type of questions. 3. ÂÚUèÿææ ÂýæÚUÖ ãôÙð ÂÚU, ÂýàÙ-ÂéçSÌ·¤æ ¥æ·¤ô Îð Îè ÁæØð»èÐ ÂãÜðU ÂUæ¡¿ ç×ÙÅU 3. At the commencement of examination, the question booklet ¥æ·¤ô ÂýàÙ-ÂéçSÌ·¤æ ¹ôÜÙð ÌÍæ ©â·¤è çÙÙçÜç¹Ì Áæ¡¿ ·ð¤ çÜ° çÎØð will be given to you. In the first 5 minutes, you are requested ÁæØð¢»ð çÁâ·¤è Áæ¡¿ ¥æ·¤ô ¥ßàØ ·¤ÚUÙè ãñ Ñ to open the booklet and compulsorily examine it as below : (i) ÂýàÙ-ÂéçSÌ·¤æ ¹ôÜÙð ·ð¤ çÜ° ©â·ð¤ ·¤ßÚU ÂðÁ¤ÂÚU Ü»è ·¤æ»Á ·¤è (i) To have access to the Question Booklet, tear off the paper âèÜ ·¤ô ȤæǸU Üð¢UÐ ¹éÜè ãé§ü Øæ çÕÙæ SÅUè·¤ÚU-âèÜU ·¤è ÂéçSÌ·¤æ seal on the edge of this cover page. Do not accept a Sßè·¤æÚU Ù ·¤Úð¢UÐ booklet without sticker-seal and do not accept an open booklet. -
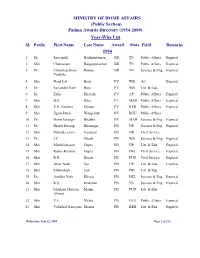
(Public Section) Padma Awards Directory (1954-2009) Year-Wise List Sl
MINISTRY OF HOME AFFAIRS (Public Section) Padma Awards Directory (1954-2009) Year-Wise List Sl. Prefix First Name Last Name Award State Field Remarks 1954 1 Dr. Sarvapalli Radhakrishnan BR TN Public Affairs Expired 2 Shri Chakravarti Rajagopalachari BR TN Public Affairs Expired 3 Dr. Chandrasekhara Raman BR TN Science & Eng. Expired Venkata 4 Shri Nand Lal Bose PV WB Art Expired 5 Dr. Satyendra Nath Bose PV WB Litt. & Edu. 6 Dr. Zakir Hussain PV AP Public Affairs Expired 7 Shri B.G. Kher PV MAH Public Affairs Expired 8 Shri V.K. Krishna Menon PV KER Public Affairs Expired 9 Shri Jigme Dorji Wangchuk PV BHU Public Affairs 10 Dr. Homi Jehangir Bhabha PB MAH Science & Eng. Expired 11 Dr. Shanti Swarup Bhatnagar PB UP Science & Eng. Expired 12 Shri Mahadeva Iyer Ganapati PB OR Civil Service 13 Dr. J.C. Ghosh PB WB Science & Eng. Expired 14 Shri Maithilisharan Gupta PB UP Litt. & Edu. Expired 15 Shri Radha Krishan Gupta PB DEL Civil Service Expired 16 Shri R.R. Handa PB PUN Civil Service Expired 17 Shri Amar Nath Jha PB UP Litt. & Edu. Expired 18 Shri Malihabadi Josh PB DEL Litt. & Edu. 19 Dr. Ajudhia Nath Khosla PB DEL Science & Eng. Expired 20 Shri K.S. Krishnan PB TN Science & Eng. Expired 21 Shri Moulana Hussain Madni PB PUN Litt. & Edu. Ahmed 22 Shri V.L. Mehta PB GUJ Public Affairs Expired 23 Shri Vallathol Narayana Menon PB KER Litt. & Edu. Expired Wednesday, July 22, 2009 Page 1 of 133 Sl. Prefix First Name Last Name Award State Field Remarks 24 Dr. -

Evaluation of the Effects of Music Therapy Using Todi Raga of Hindustani Classical Music on Blood Pressure, Pulse Rate and Respiratory Rate of Healthy Elderly Men
Volume 64, Issue 1, 2020 Journal of Scientific Research Institute of Science, Banaras Hindu University, Varanasi, India. Evaluation of the Effects of Music Therapy Using Todi Raga of Hindustani Classical Music on Blood Pressure, Pulse Rate and Respiratory Rate of Healthy Elderly Men Samarpita Chatterjee (Mukherjee) 1, and Roan Mukherjee2* 1 Department of Hindustani Classical Music (Vocal), Sangit-Bhavana, Visva-Bharati (A Central University), Santiniketan, Birbhum-731235,West Bengal, India 2 Department of Human Physiology, Hazaribag College of Dental Sciences and Hospital, Demotand, Hazaribag 825301, Jharkhand, India. [email protected] Abstract Several studies have indicated that music therapy may affect I. INTRODUCTION cardiovascular health; in particular, it may bring positive changes Music may be regarded as the projection of ideas as well as in blood pressure levels and heart rate, thereby improving the emotions through significant sounds produced by an instrument, overall quality of life. Hence, to regulate blood pressure, music voices, or both by taking into consideration different elements of therapy may be regarded as a significant complementary and alternative medicine (CAM). The respiratory rate, if maintained melody, rhythm, and harmony. Music plays an important role in within the normal range, may promote good cardiac health. The everyone’s life. Music has the power to make one experience aim of the present study was to evaluate the changes in blood harmony, emotional ecstasy, spiritual uplifting, positive pressure, pulse rate and respiratory rate in healthy and disease-free behavioral changes, and absolute tranquility. The annoyance in males (age 50-60 years), at the completion of 30 days of music life may increase in lack of melody and harmony. -

A History of Indian Music by the Same Author
68253 > OUP 880 5-8-74 10,000 . OSMANIA UNIVERSITY LIBRARY Call No.' poa U Accession No. Author'P OU H Title H; This bookok should bHeturned on or befoAbefoifc the marked * ^^k^t' below, nfro . ] A HISTORY OF INDIAN MUSIC BY THE SAME AUTHOR On Music : 1. Historical Development of Indian Music (Awarded the Rabindra Prize in 1960). 2. Bharatiya Sangiter Itihasa (Sanglta O Samskriti), Vols. I & II. (Awarded the Stisir Memorial Prize In 1958). 3. Raga O Rupa (Melody and Form), Vols. I & II. 4. Dhrupada-mala (with Notations). 5. Sangite Rabindranath. 6. Sangita-sarasamgraha by Ghanashyama Narahari (edited). 7. Historical Study of Indian Music ( ....in the press). On Philosophy : 1. Philosophy of Progress and Perfection. (A Comparative Study) 2. Philosophy of the World and the Absolute. 3. Abhedananda-darshana. 4. Tirtharenu. Other Books : 1. Mana O Manusha. 2. Sri Durga (An Iconographical Study). 3. Christ the Saviour. u PQ O o VM o Si < |o l "" c 13 o U 'ij 15 1 I "S S 4-> > >-J 3 'C (J o I A HISTORY OF INDIAN MUSIC' b SWAMI PRAJNANANANDA VOLUME ONE ( Ancient Period ) RAMAKRISHNA VEDANTA MATH CALCUTTA : INDIA. Published by Swaxni Adytaanda Ramakrishna Vedanta Math, Calcutta-6. First Published in May, 1963 All Rights Reserved by Ramakrishna Vedanta Math, Calcutta. Printed by Benoy Ratan Sinha at Bharati Printing Works, 141, Vivekananda Road, Calcutta-6. Plates printed by Messrs. Bengal Autotype Co. Private Ltd. Cornwallis Street, Calcutta. DEDICATED TO SWAMI VIVEKANANDA AND HIS SPIRITUAL BROTHER SWAMI ABHEDANANDA PREFACE Before attempting to write an elaborate history of Indian Music, I had a mind to write a concise one for the students.