DOCSLIB.ORG

View-Dependent Culling of Dynamic Systems in Virtual Environments

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
View-Dependent Culling of Dynamic Systems in Virtual Environments View-Dependent Culling of Dynamic Systems in Virtual Environments Stephen Chenney David Forsyth* University of California at Berkeley Abstract ine the implications of culling dynamic systems, and present examples to demonstrate possible modeling techniques. Scalable rendering of virtual environments requires culling objects that have no etTect on the view. This paper ex- 2 Culling Dynamics plores culling moving objects by not solving the equations of motion of objects that don’t tiect the view. While this Culling dynamics that have no visible impact offers to approach could be scalable for many kinds of environments, achieve scalability in virtual worlds, but results in two sig- it raises two problems: consistency - ensuring that objects nificant problems. that come back into view do so in the right state - and com- ● Consistency: if the view turns away from a system pleteness - ensuring that objects that would have entered of moving objects whose dynamics are then culled, in the view volume as a result of their motions, do so. what state should those objects be when the view turns Solutions to these problems lie in studying the statistics back? In particular, in an ideal system, an observer of the motion of objects. We show strategies for address- should not be able to obtain contradictions by looking ing the problem of consistency, with a number of examples away from an object, and then back at it. that illustrate both the difficulties involved in, and the po- ● tential gains to be obtained by, formulating a comprehensive Comdeteness: obiects that are out of the view vol- approach. ume often travel int~ it of their own accord - for exam- ple, consider a view into a room full of balls bouncing CR Descriptors: 1.3.7 [Computer Graphics]: Three- off walls. If the dynamics of a ball are culled as soon Dimensional Graphi@ and Realism - Virtual reality 1.6.5 as it leaves the view volume, a fixed view could contain [Simulation and Modeling]: Model Development - Mod- a steaddy decreasing number of balls. While this could eling methodologies 1.6.8 [Simulation and Modeling]: be perfectly consistent with evidence available to the Types of Simulation - Animation viewer (there could be something out of view catching the balls), it is a poor model. Avoiding this difficulty Introduction requires some way of telling where an object might be, 1 without necessarily solving its equations of motion. Dynamic systems are an important component of virtual en- A natural approach to the consistency problem involves tag- vironments. However, traditional dynamic systems require ging an object with the time it was last seen and its state at constant computation to keep their state up to date. As vir- that time when it leaves the view volume, and then advanc- tual worlds become larger in size, we expect the number of ing its state (by solving the equations of motion with as large systems with visible impact to grow at a slower pace, and a time-step as possible) when the view volume moves back less of the total dynamic state to be relevant for rendering over the object. This is a poor solution for two reasone: it a given view. To achieve maximum scalability, the cost of leads to sharp collapses in the frame rate as the view sweeps computing dynamics should depend only on what is relevant over a complex object which has been out of view for a while, to the view, not on the total size of the world. aud it offers no leverage on the completeness problem. Level of detail [8] and visibility culling [2, 7] achieve scal- In our view, a better approach involves a study of the abilityy for static worlds by rendering only what is relevant. qualitative properties of dynamic systems. A viewer will While Hodgins and Carlson[5] reduce the cost of dynamic detect an inconsistency if their qualitative prediction of eye- simulation by using level of detad for hopping robots play- tem behavior is violated, so it is at thk level that dynamic ing a chase-and-capture game, their approach requires dis- state must be consistent. Underlying our methods should tinct, hand generated models for the robot dynamics. Setae be a model of human perception of dynamics that indicates et. al. [9] present a range of models for trees moving in the which properties must be maintained, allowing us to avoid wind, each corresponding to a different quality and cost of computing expensive, irrelevant properties. simulation, but there is no discussion of how dynamic state A key property in designing a model for culling is the sen- is maintained when trees are culled. In this paper we exam- sitivity of the system to initial conditions. A viewer has a snapshot of the approximate initial conditions when a sys- ● [schenneyldaf]Qcs.berkeley.edu tem leaves the view, and it is the predictions they may make based on those conditions that determines how a new state Permission to make digitalhrd copies of all or part oftbis material for is generated when the system re-enters the view. We char- personal Orckxroom use is granted without fee provided that tie copies acterize the intluence of initial conditions in three ways, and sre not made or distributed for profit or commercial advantage, tbe copy- associate diEerent strategies with each. right notice, tbe title oftbe publication and its date ~ppe.u,and notice is ● Strong influence allows accurate predictions to be giversthat copyright is by permission of tbe ACM, Inc. To copy otherwise, made, leaving no choice but to integrate the system to republish, to post on servers or to redistribute to lists, requires specific permission and/or f~. as if it were in view. However, this may introduce lag. 1997 Symposium on Interactive 3D C@sbics, Providence RI [JSA As a paztial solution to this problem we attempt to Copy-igbt 1997 ACM0-89791-884-3197104..$3.50 buHer state ahead of time, aiming to have state ready when the system re-enters the view. This does not save 55 work, but does spread the lag time over many preceding frames. ‘t ● Medium influence allows a viewer to make some qual- itative predictions. There appears to be no completely general modeling strategy for this case. Instead we ex- pect to find a set of techniques, each of which works for a class of dynamics, and apply those which best match the properties of a given system. One applicable tech- nique is classical perturbation theory, as described in [1], which models how systems behave over time when subjected to small perturbations in control. ● Weak influence makes it difficult for a viewer to make any prediction about state baaed on their knowledge -4 I I of initial conditions. However, predictions can still be o 5 10152025303540 4550 made baaed on knowledge of the general behavior of CycleNumber the system - for example, energy or angular momentum might be conserved. To generate a new state in this Figure 1: A trace of the difference in # for two cars started scenario we encode the general behavior of the system with similar initial wnditions. The value of the difference is using statistical or other means, then choose a new state noise-like after a small number of cycles, meaning that the consistent with our model. relationship between the 2 cars becomes dificult to predict after only a few cycles. In turn, this means the system’s We refer to this intluence of initial conditions as conditioning. dynamics can be culled quite easily, because a viewer is un- A key parameter in defining culling strategies is the time likely to be able to make sufficiently accurate predictions to that must elapse before strong conditioning is replaced by notice an error, if invariant properties of the motion can be medium and then weak. In the following sections we discuss preserved. some possible approaches to determining these time intervals such that the important qualitative measures of a system remain consistent. systems of thk form possess one or more attractors, to which We have implemented a virtual fun park environment in the state of the system will move regardless of initial condi- which to experiment with these ideaa. The core system loops tions. A an attractor in state space offers a useful model of testing visibility and then updating the dynamics and ren- the general behavior of the system – regardless of how the dering the geometry for visible objects only. The dynamic models are all designed such that they may be called at ar- system has evolved, it will lie on an attractor. bitrary time intervals as they move into and out of view. The run phase of the Tilt-A-Whirl, when ~ = 6.5rpm, Here we examine two systems designed for use within this exhibits chaotic steady state dynamics, which are described environment – the Tilt-A-Whirl and a bumper car ride. in detail in [6]. Figure 1 compares the motion of 2 cars that begin with similar initial condkions corresponding to 3 The Tilt-A-Whirl a difference of 10° and 10° /s for # and & The sequence indicates that after the cars have passed over 3 hills (which The Tilt-A-Whirl is an amusement park ride in which pas- takes around 9s of virtuaf time), there is a wide variation in sengers sit in one of seven cars that are driven in unison which car follows which, and by how much. around a holly circular track. Each car is free to rotate about The Tilt-a-Whirl’s attractor is an invariant property of the center of a circular platform which tilts such that it re- the motion – any Tilt-a-Whirl that has been running for mains tangential to the surface aa it moves around the track.
Load more

Recommended publications
  • Chapter 6: Ensemble Forecasting and Atmospheric Predictability
    Chapter 6: Ensemble Forecasting and Atmospheric Predictability Introduction Deterministic Chaos (what!?) In 1951 Charney indicated that forecast skill would break down, but he attributed it to model errors and errors in the initial conditions… In the 1960’s the forecasts were skillful for only one day or so. Statistical prediction was equal or better than dynamical predictions, Like it was until now for ENSO predictions! Lorenz wanted to show that statistical prediction could not match prediction with a nonlinear model for the Tokyo (1960) NWP conference So, he tried to find a model that was not periodic (otherwise stats would win!) He programmed in machine language on a 4K memory, 60 ops/sec Royal McBee computer He developed a low-order model (12 d.o.f) and changed the parameters and eventually found a nonperiodic solution Printed results with 3 significant digits (plenty!) Tried to reproduce results, went for a coffee and OOPS! Lorenz (1963) discovered that even with a perfect model and almost perfect initial conditions the forecast loses all skill in a finite time interval: “A butterfly in Brazil can change the forecast in Texas after one or two weeks”. In the 1960’s this was only of academic interest: forecasts were useless in two days Now, we are getting closer to the 2 week limit of predictability, and we have to extract the maximum information Central theorem of chaos (Lorenz, 1960s): a) Unstable systems have finite predictability (chaos) b) Stable systems are infinitely predictable a) Unstable dynamical system b) Stable dynamical
    [Show full text]
  • A Gentle Introduction to Dynamical Systems Theory for Researchers in Speech, Language, and Music
    A Gentle Introduction to Dynamical Systems Theory for Researchers in Speech, Language, and Music. Talk given at PoRT workshop, Glasgow, July 2012 Fred Cummins, University College Dublin [1] Dynamical Systems Theory (DST) is the lingua franca of Physics (both Newtonian and modern), Biology, Chemistry, and many other sciences and non-sciences, such as Economics. To employ the tools of DST is to take an explanatory stance with respect to observed phenomena. DST is thus not just another tool in the box. Its use is a different way of doing science. DST is increasingly used in non-computational, non-representational, non-cognitivist approaches to understanding behavior (and perhaps brains). (Embodied, embedded, ecological, enactive theories within cognitive science.) [2] DST originates in the science of mechanics, developed by the (co-)inventor of the calculus: Isaac Newton. This revolutionary science gave us the seductive concept of the mechanism. Mechanics seeks to provide a deterministic account of the relation between the motions of massive bodies and the forces that act upon them. A dynamical system comprises • A state description that indexes the components at time t, and • A dynamic, which is a rule governing state change over time The choice of variables defines the state space. The dynamic associates an instantaneous rate of change with each point in the state space. Any specific instance of a dynamical system will trace out a single trajectory in state space. (This is often, misleadingly, called a solution to the underlying equations.) Description of a specific system therefore also requires specification of the initial conditions. In the domain of mechanics, where we seek to account for the motion of massive bodies, we know which variables to choose (position and velocity).
    [Show full text]
  • An Image Cryptography Using Henon Map and Arnold Cat Map
    International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 Volume: 05 Issue: 04 | Apr-2018 www.irjet.net p-ISSN: 2395-0072 An Image Cryptography using Henon Map and Arnold Cat Map. Pranjali Sankhe1, Shruti Pimple2, Surabhi Singh3, Anita Lahane4 1,2,3 UG Student VIII SEM, B.E., Computer Engg., RGIT, Mumbai, India 4Assistant Professor, Department of Computer Engg., RGIT, Mumbai, India ---------------------------------------------------------------------***--------------------------------------------------------------------- Abstract - In this digital world i.e. the transmission of non- 2. METHODOLOGY physical data that has been encoded digitally for the purpose of storage Security is a continuous process via which data can 2.1 HENON MAP be secured from several active and passive attacks. Encryption technique protects the confidentiality of a message or 1. The Henon map is a discrete time dynamic system information which is in the form of multimedia (text, image, introduces by michel henon. and video).In this paper, a new symmetric image encryption 2. The map depends on two parameters, a and b, which algorithm is proposed based on Henon’s chaotic system with for the classical Henon map have values of a = 1.4 and byte sequences applied with a novel approach of pixel shuffling b = 0.3. For the classical values the Henon map is of an image which results in an effective and efficient chaotic. For other values of a and b the map may be encryption of images. The Arnold Cat Map is a discrete system chaotic, intermittent, or converge to a periodic orbit. that stretches and folds its trajectories in phase space. Cryptography is the process of encryption and decryption of 3.
    [Show full text]
  • WHAT IS a CHAOTIC ATTRACTOR? 1. Introduction J. Yorke Coined the Word 'Chaos' As Applied to Deterministic Systems. R. Devane
    WHAT IS A CHAOTIC ATTRACTOR? CLARK ROBINSON Abstract. Devaney gave a mathematical definition of the term chaos, which had earlier been introduced by Yorke. We discuss issues involved in choosing the properties that characterize chaos. We also discuss how this term can be combined with the definition of an attractor. 1. Introduction J. Yorke coined the word `chaos' as applied to deterministic systems. R. Devaney gave the first mathematical definition for a map to be chaotic on the whole space where a map is defined. Since that time, there have been several different definitions of chaos which emphasize different aspects of the map. Some of these are more computable and others are more mathematical. See [9] a comparison of many of these definitions. There is probably no one best or correct definition of chaos. In this paper, we discuss what we feel is one of better mathematical definition. (It may not be as computable as some of the other definitions, e.g., the one by Alligood, Sauer, and Yorke.) Our definition is very similar to the one given by Martelli in [8] and [9]. We also combine the concepts of chaos and attractors and discuss chaotic attractors. 2. Basic definitions We start by giving the basic definitions needed to define a chaotic attractor. We give the definitions for a diffeomorphism (or map), but those for a system of differential equations are similar. The orbit of a point x∗ by F is the set O(x∗; F) = f Fi(x∗) : i 2 Z g. An invariant set for a diffeomorphism F is an set A in the domain such that F(A) = A.
    [Show full text]
  • Thermodynamic Properties of Coupled Map Lattices 1 Introduction
    Thermodynamic properties of coupled map lattices J´erˆome Losson and Michael C. Mackey Abstract This chapter presents an overview of the literature which deals with appli- cations of models framed as coupled map lattices (CML’s), and some recent results on the spectral properties of the transfer operators induced by various deterministic and stochastic CML’s. These operators (one of which is the well- known Perron-Frobenius operator) govern the temporal evolution of ensemble statistics. As such, they lie at the heart of any thermodynamic description of CML’s, and they provide some interesting insight into the origins of nontrivial collective behavior in these models. 1 Introduction This chapter describes the statistical properties of networks of chaotic, interacting el- ements, whose evolution in time is discrete. Such systems can be profitably modeled by networks of coupled iterative maps, usually referred to as coupled map lattices (CML’s for short). The description of CML’s has been the subject of intense scrutiny in the past decade, and most (though by no means all) investigations have been pri- marily numerical rather than analytical. Investigators have often been concerned with the statistical properties of CML’s, because a deterministic description of the motion of all the individual elements of the lattice is either out of reach or uninteresting, un- less the behavior can somehow be described with a few degrees of freedom. However there is still no consistent framework, analogous to equilibrium statistical mechanics, within which one can describe the probabilistic properties of CML’s possessing a large but finite number of elements.
    [Show full text]
  • Nonlinear Dynamics and Entropy of Complex Systems with Hidden and Self-Excited Attractors
    entropy Editorial Nonlinear Dynamics and Entropy of Complex Systems with Hidden and Self-Excited Attractors Christos K. Volos 1,* , Sajad Jafari 2 , Jacques Kengne 3 , Jesus M. Munoz-Pacheco 4 and Karthikeyan Rajagopal 5 1 Laboratory of Nonlinear Systems, Circuits & Complexity (LaNSCom), Department of Physics, Aristotle University of Thessaloniki, Thessaloniki 54124, Greece 2 Nonlinear Systems and Applications, Faculty of Electrical and Electronics Engineering, Ton Duc Thang University, Ho Chi Minh City 700000, Vietnam; [email protected] 3 Department of Electrical Engineering, University of Dschang, P.O. Box 134 Dschang, Cameroon; [email protected] 4 Faculty of Electronics Sciences, Autonomous University of Puebla, Puebla 72000, Mexico; [email protected] 5 Center for Nonlinear Dynamics, Institute of Research and Development, Defence University, P.O. Box 1041 Bishoftu, Ethiopia; [email protected] * Correspondence: [email protected] Received: 1 April 2019; Accepted: 3 April 2019; Published: 5 April 2019 Keywords: hidden attractor; complex systems; fractional-order; entropy; chaotic maps; chaos In the last few years, entropy has been a fundamental and essential concept in information theory. It is also often used as a measure of the degree of chaos in systems; e.g., Lyapunov exponents, fractal dimension, and entropy are usually used to describe the complexity of chaotic systems. Thus, it will be important to study entropy in nonlinear systems. Additionally, there has been an increasing interest in a new classification of nonlinear dynamical systems including two kinds of attractors: self-excited attractors and hidden attractors. Self-excited attractors can be localized straightforwardly by applying a standard computational procedure.
    [Show full text]
  • Chaos: the Mathematics Behind the Butterfly Effect
    Chaos: The Mathematics Behind the Butterfly E↵ect James Manning Advisor: Jan Holly Colby College Mathematics Spring, 2017 1 1. Introduction A butterfly flaps its wings, and a hurricane hits somewhere many miles away. Can these two events possibly be related? This is an adage known to many but understood by few. That fact is based on the difficulty of the mathematics behind the adage. Now, it must be stated that, in fact, the flapping of a butterfly’s wings is not actually known to be the reason for any natural disasters, but the idea of it does get at the driving force of Chaos Theory. The common theme among the two is sensitive dependence on initial conditions. This is an idea that will be revisited later in the paper, because we must first cover the concepts necessary to frame chaos. This paper will explore one, two, and three dimensional systems, maps, bifurcations, limit cycles, attractors, and strange attractors before looking into the mechanics of chaos. Once chaos is introduced, we will look in depth at the Lorenz Equations. 2. One Dimensional Systems We begin our study by looking at nonlinear systems in one dimen- sion. One of the important features of these is the nonlinearity. Non- linearity in an equation evokes behavior that is not easily predicted due to the disproportionate nature of inputs and outputs. Also, the term “system”isoftenamisnomerbecauseitoftenevokestheideaof asystemofequations.Thiswillbethecaseaswemoveourfocuso↵ of one dimension, but for now we do not want to think of a system of equations. In this case, the type of system we want to consider is a first-order system of a single equation.
    [Show full text]
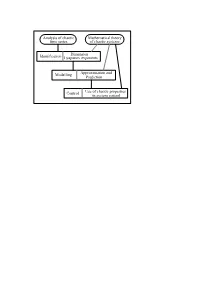
  • Analysis of Chaotic Time Series Mathematical Theory of Chaotic
    Analysis of chaotic Mathematical theory time series of chaotic systems Dimension Identification Lyapunov exponents Approximation and Modelling Prediction Control Use of chaotic properties in system control Chaotic time series Part I Estimation of invariant prop eries in state space y D Kugiumtzis B Lillekjendlie N Christophersen y January Abs tra ct Certain deterministic nonlinear systems may show chaotic b ehaviour Time series de rived from such systems seem sto chastic when analyzed with linear techniques However uncovering the deterministic structure is important because it allows for construction of more realistic and better models and thus improved predictive capabilities This pap er describ es key features of chaotic systems including strange attractors and Lyapunov expo nents The emphasis is on state space reconstruction techniques that are used to estimate these properties given scalar observations Data generated from equations known to display chaotic behaviour are used for illustration A compilation of applications to real data from widely dierent elds is given If chaos is found to b e present one may proceed to build nonlinear models which is the topic of the second pap er in this series Intro du ct ion Chaotic behaviour in deterministic dynamical systems is an intrinsicly nonlinear phenomenon A characteristic feature of chaotic systems is an extreme sensitivity to changes in initial con ditions while the dynamics at least for socalled dissipative systems is still constrained to a nite region of state space called a strange
    [Show full text]
  • Random Boolean Networks As a Toy Model for the Brain
    UNIVERSITY OF GENEVA SCIENCE FACULTY VRIJE UNIVERSITEIT OF AMSTERDAM PHYSICS SECTION Random Boolean Networks as a toy model for the brain MASTER THESIS presented at the science faculty of the University of Geneva for obtaining the Master in Theoretical Physics by Chlo´eB´eguin Supervisor (VU): Pr. Greg J Stephens Co-Supervisor (UNIGE): Pr. J´er^ome Kasparian July 2017 Contents Introduction1 1 Biology, physics and the brain4 1.1 Biological description of the brain................4 1.2 Criticality in the brain......................8 1.2.1 Physics reminder..................... 10 1.2.2 Experimental evidences.................. 15 2 Models of neural networks 20 2.1 Classes of models......................... 21 2.1.1 Spiking models...................... 21 2.1.2 Rate-based models.................... 23 2.1.3 Attractor networks.................... 24 2.1.4 Links between the classes of models........... 25 2.2 Random Boolean Networks.................... 28 2.2.1 General definition..................... 28 2.2.2 Kauffman network.................... 30 2.2.3 Hopfield network..................... 31 2.2.4 Towards a RBN for the brain.............. 32 2.2.5 The model......................... 33 3 Characterisation of RBNs 34 3.1 Attractors............................. 34 3.2 Damage spreading........................ 36 3.3 Canonical specific heat...................... 37 4 Results 40 4.1 One population with Gaussian weights............. 40 4.2 Dale's principle and balance of inhibition - excitation..... 46 4.3 Lognormal distribution of the weights.............. 51 4.4 Discussion............................. 55 i 5 Conclusion 58 Bibliography 60 Acknowledgements 66 A Python Code 67 A.1 Dynamics............................. 67 A.2 Attractor search.......................... 69 A.3 Hamming Distance........................ 73 A.4 Canonical specific heat.....................
    [Show full text]
  • January 3, 2019 Dynamical Systems B. Solomyak LECTURE 11
    January 3, 2019 Dynamical Systems B. Solomyak LECTURE 11 SUMMARY 1. Hyperbolic toral automorphisms (cont.) d d d Let A be d × d integer matrix, with det A = ±1. Consider T = R =Z (the d- dimensional torus). d Definition 1.1. The map TA(x) = Ax (mod Z ) is called the toral automorphism asso- ciated with A. d Proposition 1.2. TA is a group automorphism; in fact, every automorphism of T has such a form. Definition 1.3. The automorphism is called hyperbolic if A is hyperbolic, that is, A has no eigenvalues of absolute value one. " # 2 1 Example 1.4 (Arnold's \cat map"). This is TA for A = . 1 1 Theorem 1.5 (see [1, x2.4]). Every hyperbolic toral automorphism is chaotic. We will see the proof for d = 2, for simplicity, following [1, 2]. The proof will be broken into lemmas. The first one was already covered on December 27. m n 2 Lemma 1.6. The points with rational coordinates f( k ; k ); m; n; k 2 Ng (mod Z ) are 2 dense in T , and they are all periodic for TA. Lemma 1.7. Let A be a hyperbolic 2×2 matrix. Thus it has two real eigenvalues: jλ1j > 1 and jλ2j < 1. Then the eigenvalues are irrational and the eigenvectors have irrational slopes. Let Es, Eu be the stable and unstable subspaces for A, respectively; they are one- dimensional and are spanned by the eigenvectors. s u Consider the point 0 = (0; 0) on the torus; it is fixed by TA.
    [Show full text]
  • THE BUTTERFLY EFFECT Étienne GHYS CNRS-UMPA ENS Lyon [email protected]
    12th International Congress on Mathematical Education Program Name XX-YY-zz (pp. abcde-fghij) 8 July – 15 July, 2012, COEX, Seoul, Korea (This part is for LOC use only. Please do not change this part.) THE BUTTERFLY EFFECT Étienne GHYS CNRS-UMPA ENS Lyon [email protected] It is very unusual for a mathematical idea to disseminate into the society at large. An interesting example is chaos theory, popularized by Lorenz’s butterfly effect: “does the flap of a butterfly’s wings in Brazil set off a tornado in Texas?” A tiny cause can generate big consequences! Can one adequately summarize chaos theory in such a simple minded way? Are mathematicians responsible for the inadequate transmission of their theories outside of their own community? What is the precise message that Lorenz wanted to convey? Some of the main characters of the history of chaos were indeed concerned with the problem of communicating their ideas to other scientists or non-scientists. I’ll try to discuss their successes and failures. The education of future mathematicians should include specific training to teach them how to explain mathematics outside their community. This is more and more necessary due to the increasing complexity of mathematics. A necessity and a challenge! INTRODUCTION In 1972, the meteorologist Edward Lorenz gave a talk at the 139th meeting of the American Association for the Advancement of Science entitled “Does the flap of a butterfly’s wings in Brazil set off a tornado in Texas?”. Forty years later, a google search “butterfly effect” generates ten million answers.
    [Show full text]
  • Fractal-Bits
    fractal-bits Claude Heiland-Allen 2012{2019 Contents 1 buddhabrot/bb.c . 3 2 buddhabrot/bbcolourizelayers.c . 10 3 buddhabrot/bbrender.c . 18 4 buddhabrot/bbrenderlayers.c . 26 5 buddhabrot/bound-2.c . 33 6 buddhabrot/bound-2.gnuplot . 34 7 buddhabrot/bound.c . 35 8 buddhabrot/bs.c . 36 9 buddhabrot/bscolourizelayers.c . 37 10 buddhabrot/bsrenderlayers.c . 45 11 buddhabrot/cusp.c . 50 12 buddhabrot/expectmu.c . 51 13 buddhabrot/histogram.c . 57 14 buddhabrot/Makefile . 58 15 buddhabrot/spectrum.ppm . 59 16 buddhabrot/tip.c . 59 17 burning-ship-series-approximation/BossaNova2.cxx . 60 18 burning-ship-series-approximation/BossaNova.hs . 81 19 burning-ship-series-approximation/.gitignore . 90 20 burning-ship-series-approximation/Makefile . 90 21 .gitignore . 90 22 julia/.gitignore . 91 23 julia-iim/julia-de.c . 91 24 julia-iim/julia-iim.c . 94 25 julia-iim/julia-iim-rainbow.c . 94 26 julia-iim/julia-lsm.c . 98 27 julia-iim/Makefile . 100 28 julia/j-render.c . 100 29 mandelbrot-delta-cl/cl-extra.cc . 110 30 mandelbrot-delta-cl/delta.cl . 111 31 mandelbrot-delta-cl/Makefile . 116 32 mandelbrot-delta-cl/mandelbrot-delta-cl.cc . 117 33 mandelbrot-delta-cl/mandelbrot-delta-cl-exp.cc . 134 34 mandelbrot-delta-cl/README . 139 35 mandelbrot-delta-cl/render-library.sh . 142 36 mandelbrot-delta-cl/sft-library.txt . 142 37 mandelbrot-laurent/DM.gnuplot . 146 38 mandelbrot-laurent/Laurent.hs . 146 39 mandelbrot-laurent/Main.hs . 147 40 mandelbrot-series-approximation/args.h . 148 41 mandelbrot-series-approximation/emscripten.cpp . 150 42 mandelbrot-series-approximation/index.html .
    [Show full text]