The Effectiveness of the National Board Certification As It Relates to the Advanced Placement Calculus AB Exam
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Westland Writes on Time
Westland Writes 2011: On Time Copyright 2011 by the author of this book Westland (MI) Public Library (Andy Schuck, editor). Each author retains sole copyright to his or her contributions to this book. The William P. Faust Westland Public Library 6123 Central City Parkway Westland, MI 48185 (734) 326-6123 www. westlandlibra.ry .org Andy Schuck, editor The Blurb-provided layout designs and graphic elements are copyright Blurb Inc., 2009. This book was created using the John Capraro, fiction ed. Blurb creative publishing service. The book author retains sole Patrick Franks, poetry ed. copyright to his or her contributions to this book. blurb.com A. Supreme Joseph Phillips For a day 29 The Systemis ofProcyon 49 JayezWard Cheryl Vatcher-Martin My heart belongs to you 32 The Kingsley House ghost story 61 I'm remembering love 33 Imelda Zamora 6s Shari Welch For your eyes only 35 By the water 36 Hello Richard Zerndt 36 untitled STORIES 38 Jackie Bonett A day in the life 39 Andy Dubyckyj The Atlantic is uiciou.s 40 Blair Miller Chapter: Rage ofAngels 43 Poems 9 Westland Writes 2011 On Time Regan Byers make me something committed I'm hungry I don't fucking care what time it is. Got me a good woman? Of course 1 do. She says she's always there for me. She makes me dinner Damn straight you are. cleans my ashtrays washes my clothes buys my smokes gives me whatever I want premature expectoration She never questions anything says "oku to everything Angry cause she loves me. little online warrior She needs me brandishing I'm a truth teller your keyboard mace 1 told those kids and your screen shield what she's worth you rant what they're worth and spew she heard that truth and she still came back. -

Congressional Record—Senate S777
January 31, 2019 CONGRESSIONAL RECORD — SENATE S777 States-Jordan Defense Cooperation Act of tary support funding to Israel. It reaf- vacuum that terrorists and others will 2015, and to halt the wholesale slaughter of firms the U.S. commitment to ensuring step in to fill. Our too-hasty with- the Syrian people, and for other purposes. that Israel has better weapons and drawal from Iraq, on a timeline we an- Mitch McConnell, Pat Roberts, Shelley equipment than its enemies. It will nounced to our enemies, created the Moore Capito, Mitt Romney, Richard Burr, John Cornyn, Rick Scott, Mike also foster increased technical coopera- circumstances that allowed for the rise Crapo, Cindy Hyde-Smith, Michael B. tion between Israel and the United of ISIS. We need to be wary about al- Enzi, Kevin Cramer, Mike Braun, John States to support the security of both lowing something like that to happen Boozman, Steve Daines, James M. of our countries. again. Inhofe, Thom Tillis, Joni Ernst. The legislation also strengthens our Terrorist groups are not the only en- f relationship with another close ally of tities we have to worry about. Adver- ours in the Middle East, the Kingdom saries like Russia and Iran are already NATURAL RESOURCES MANAGE- of Jordan. The Senate Intelligence trying to flex their power in the Middle MENT ACT—MOTION TO PROCEED Committee hearing on Tuesday was a East and would be more than happy to Mr. MCCONNELL. I move to proceed timely reminder of the importance of take advantage of an early U.S. with- to Calendar No. -
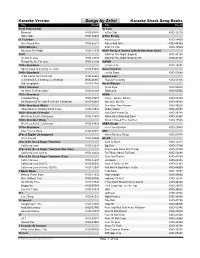
Karaoke Version Song Book
Karaoke Version Songs by Artist Karaoke Shack Song Books Title DiscID Title DiscID (Hed) Planet Earth 50 Cent Blackout KVD-29484 In Da Club KVD-12410 Other Side KVD-29955 A Fine Frenzy £1 Fish Man Almost Lover KVD-19809 One Pound Fish KVD-42513 Ashes And Wine KVD-44399 10000 Maniacs Near To You KVD-38544 Because The Night KVD-11395 A$AP Rocky & Skrillex & Birdy Nam Nam (Duet) 10CC Wild For The Night (Explicit) KVD-43188 I'm Not In Love KVD-13798 Wild For The Night (Explicit) (R) KVD-43188 Things We Do For Love KVD-31793 AaRON 1930s Standards U-Turn (Lili) KVD-13097 Santa Claus Is Coming To Town KVD-41041 Aaron Goodvin 1940s Standards Lonely Drum KVD-53640 I'll Be Home For Christmas KVD-26862 Aaron Lewis Let It Snow, Let It Snow, Let It Snow KVD-26867 That Ain't Country KVD-51936 Old Lamplighter KVD-32784 Aaron Watson 1950's Standard Outta Style KVD-55022 An Affair To Remember KVD-34148 That Look KVD-50535 1950s Standards ABBA Crawdad Song KVD-25657 Gimme Gimme Gimme KVD-09159 It's Beginning To Look A Lot Like Christmas KVD-24881 My Love, My Life KVD-39233 1950s Standards (Male) One Man, One Woman KVD-39228 I Saw Mommy Kissing Santa Claus KVD-29934 Under Attack KVD-20693 1960s Standard (Female) Way Old Friends Do KVD-32498 We Need A Little Christmas KVD-31474 When All Is Said And Done KVD-30097 1960s Standard (Male) When I Kissed The Teacher KVD-17525 We Need A Little Christmas KVD-31475 ABBA (Duet) 1970s Standards He Is Your Brother KVD-20508 After You've Gone KVD-27684 ABC 2Pac & Digital Underground When Smokey Sings KVD-27958 I Get Around KVD-29046 AC-DC 2Pac & Dr. -

New Karaoke April 16 2020.Pdf
TITLE (New songs) June 7, 2018 ARTIST Artist Change Of Heart, A 1975 Heart Out 1975 Somebody Else 1975 City Of Angels 30 Seconds To Mars Girls Talk Boys 5 Seconds Of Summer Wild For The Night (Explicit) A$AP Rocky & Skrillex & Birdy Nam Nam You Ain't Got A Hold Me AC/DC Do What Ya Gotta Do Adams, Bryan Don't Even Try Adams, Bryan Hey Afrojack Celice A-Ha Here I Stand And Face The Rain A-Ha Velvet A-Ha Don't Wanna Fight Alabama Shakes Road Less Traveled Alaina, Lauren Asphalt Cowboy Aldean, Jason Little More Summertime, A Aldean, Jason This Plane Don't Go There Aldean, Jason Uh La La La Alexia I Feel Like Dancin' All Time Low Missing You All Time Low Take Cover All Time Low As Long As I Got You Allen, Lily Friday Night Allen, Lily Him Allen, Lily Sheezus (Explicit) Allen, Lily Caroline Amine Thousand Oceans, A Amos, Tori I'll Find My Way Home Anderson, Jon & Vangelis Heroes Of Sand Angra Nothing To Say Angra Nova Era Angra Rebirth Angra Boys, And The Angus & Julia Stone Not Strong Enough Apocalyptica Black Treacle Arctic Monkeys Brianstorm Arctic Monkeys Can I Be Him Arthur, James Say You Won't Let Go Arthur, James Forever Country Artists Of Then, Now & Forever Prophecy, A Asking Alexandria Angels On My Side Astley, Rick God Says Astley, Rick Keep Singing Astley, Rick The Final Sacrifice Avantasia We Go Home Avener & Adam Cohen Without You Ayo 212 (Explicit) Azealia Banks & Lazy J TITLE (New songs) June 7, 2018 ARTIST Artist ATM Jam (Explicit) Azealia Banks & Pharrell Williams (Duet) Elastic Heart Bailey, Madilyn Stay With Me Bailey, Madilyn -

The Immaculate Secret by J.B
The Immaculate Secret By J.B. Storey WGA# 980361 J.B. Storey 1401 North 40th Street Seattle, WA 98103 USA T: 206-633-5774 C: 206-550-7130 E: [email protected] 2 FADE IN: EXT. THE UNIVERSE A swift voyage through the cosmos. The journey reaches its destination… EARTH. THE EARTH’S SURFACE We see volcanoes erupting, giant hailstorms RAINING down from the skies and tsunamis CRASHING upon the shore. CLOSER INLAND, a mountain range, where thousands of beings are locked in a FEROCIOUS battle. On one side DEMONIC CREATURES, force their way up an imposing mountain. FEMALE VOICE (VO) In the beginning, a war was waged for control of the physical realm, between the princes of heaven – the Seraphim – and the servants of Hell – the Malevores. Atop the mountain, leading into the sky, an empyreal SWIRLING LIGHT… A GATEWAY TO THE HEAVENS. Defending the mountaintop are FOUR ANGELIC TITANS (Seraphim), armed with gold swords, and covered in silver body armor. THOUSANDS of Malevore bodies are scattered everywhere. Likewise, DOZENS of dead Seraphim freckle the mountaintop. The SERAPHIM are winning through sheer, superhuman strength. Finally… four Malevore remain… their features covered by bronze facemasks. FEMALE VOICE (VO) By the end, the Malevores were all but destroyed. Each carries a weapon - Sword & Dagger, Lance, Mace and Battle Axe - marked with a small emblem depicting two entwined serpents. The Malevores DROP their weapons and SINK, with a GRISLY WAIL, into the ground. 3 FEMALE VOICE (VO) Those that survived were imprisoned in a subterranean dimension. Their tools of destruction remained their only connection to the world of the living. -

Karaoke Catalog Updated On: 09/04/2018 Sing Online on Entire Catalog
Karaoke catalog Updated on: 09/04/2018 Sing online on www.karafun.com Entire catalog TOP 50 Tennessee Whiskey - Chris Stapleton My Way - Frank Sinatra Wannabe - Spice Girls Perfect - Ed Sheeran Take Me Home, Country Roads - John Denver Broken Halos - Chris Stapleton Sweet Caroline - Neil Diamond All Of Me - John Legend Sweet Child O'Mine - Guns N' Roses Don't Stop Believing - Journey Jackson - Johnny Cash Thinking Out Loud - Ed Sheeran Uptown Funk - Bruno Mars Wagon Wheel - Darius Rucker Neon Moon - Brooks & Dunn Friends In Low Places - Garth Brooks Fly Me To The Moon - Frank Sinatra Always On My Mind - Willie Nelson Girl Crush - Little Big Town Zombie - The Cranberries Ice Ice Baby - Vanilla Ice Folsom Prison Blues - Johnny Cash Piano Man - Billy Joel (Sittin' On) The Dock Of The Bay - Otis Redding Bohemian Rhapsody - Queen Turn The Page - Bob Seger Total Eclipse Of The Heart - Bonnie Tyler Ring Of Fire - Johnny Cash Me And Bobby McGee - Janis Joplin Man! I Feel Like A Woman! - Shania Twain Summer Nights - Grease House Of The Rising Sun - The Animals Strawberry Wine - Deana Carter Can't Help Falling In Love - Elvis Presley At Last - Etta James I Will Survive - Gloria Gaynor My Girl - The Temptations Killing Me Softly - The Fugees Jolene - Dolly Parton Before He Cheats - Carrie Underwood Amarillo By Morning - George Strait Love Shack - The B-52's Crazy - Patsy Cline I Want It That Way - Backstreet Boys In Case You Didn't Know - Brett Young Let It Go - Idina Menzel These Boots Are Made For Walkin' - Nancy Sinatra Livin' On A Prayer - Bon -

Rita Ora Rip Free Mp3 Downloads
Rita ora rip free mp3 downloads ( MB) Stream and Download song R.I.P. by United Kingdom artist Rita Ora Ft. Tinie Tempah on Dawn Foxes Music - Watch the video, get the download or listen to Rita Ora – R.I.P. (feat. Tinie Tempah) for free. R.I.P. (feat. Tinie Tempah) appears on the album ORA (Deluxe. R.i.p. Ft. Tinie Tempah. Artist: Rita Ora. MB · R.i.p. (ft. Tinie Tempah) (gregor Salto Us Radio Edit). Artist: Rita Ora. MB. Rip. Artist: Rita Ora Ft. Tinie Tempah. MB · Rip. Artist: Rita Ora Feat. Tinie Tempah. MB. Advertisement. Related Searches. Rita Ora Feat. Tinie Tempah R.I.P free mp3 download and stream. Download Rita Ora Rip, MB Mp3 Single Track Rita Ora Rip Released On Download This Song In Mp3 And Othe Available Formats. Download Rita Ora R I P Mp3clan Com, MB Mp3 Single Track Rita Ora R I P Mp3clan Com Released On Download This Song In Mp3 And Othe Available. Stream R.I.P. (ft. Tinie Tempah) by Rita Ora from desktop or your mobile device. Buy R.I.P.: Read 2 Digital Music Reviews - Start your day free trial of Unlimited to listen to this album plus tens of Add to MP3 Cart . Haven't heard much more of Rita Ora's music but will be looking for more in the future. Download "R.I.P." on iTunes right now! Click here: More Rita Ora on iTunes. Tinie Tempah Rip Free Mp3 Download. Free download Rita Ora Tinie Tempah Rip Free Mp3 Download mp3 for free Tinie Tempah - R. -
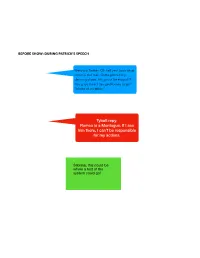
Rj Final Running Text
BEFORE SHOW—DURING PATRICK’S SPEECH Mercutio Twitter: Oh hell yes! Look what came in the mail. Gotta get out my dancing shoes. It’s gonna be #capuLIT… You guys think I can get Romeo to go? *photo of invitation* Tybalt repy: Romeo is a Montague. If I see him there, I can’t be responsible for my actions. Sabrina, this could be where a test of the system could go! REEL ONE: SCENE ONE JULIET (V.O.) Two households, both alike in dignity, In fair Verona, where we lay our scene, From ancient grudge break to new mutiny, Where civil blood makes civil hands unclean. From forth the fatal loins of these two foes A pair of star-cross'd lovers take their life; Whose misadventured piteous overthrows It’s going down! Tybalt better watch Do with their death bury their parents' strife. out. #DogsBeatCATS The fearful passage of their death-mark'd love, And the continuance of their parents' rage, Which, but their children's end, nought could remove, Is now the two hours' traffic of our stage; The which if you with patient ears attend, What here shall miss, our toil shall strive to mend. Chaos, violence, pandemonium. Some Shakespeare, some shouts, some cries, some contemporary speaking. As it peaks, we here a blaring alert sound and a message appears across the scene: Stand by for an announcement from Prince Escalus ALERT FROM THE OFFICE OF THE PRINCE: Lay down your weapons! All parties must IMMEDIATELY cease REEL ONE: SCENE 2 bandying and leave the city center of Verona. -

Karaoke Catalog Updated On: 08/09/2016 Sing Online on Entire Catalog
Karaoke catalog Updated on: 08/09/2016 Sing online on www.karafun.com Entire catalog TOP 50 Uptown Funk - Bruno Mars Crazy - Patsy Cline Summer Of '69 - Bryan Adams Don't Stop Believing - Journey Love Yourself - Justin Bieber Shake It Off - Taylor Swift Sweet Caroline - Neil Diamond My Girl - The Temptations Like I'm Gonna Lose You - Meghan Trainor Girl Crush - Little Big Town Wagon Wheel - Darius Rucker Ex's & Oh's - Elle King Tennessee Whiskey - Chris Stapleton Before He Cheats - Carrie Underwood Black Velvet - Alannah Myles Let It Go - Idina Menzel Me Too - Meghan Trainor Baby Got Back - Sir Mix-a-Lot EXPLICIT Bohemian Rhapsody - Queen House Of The Rising Sun - The Animals H.O.L.Y. - Florida Georgia Line Hello - Adele Sweet Home Alabama - Lynyrd Skynyrd When We Were Young - Adele Ring Of Fire - Johnny Cash Jackson - Johnny Cash Take Me Home, Country Roads - John Denver Summer Nights - Grease Sweet Child O'Mine - Guns N' Roses Unchained Melody - The Righteous Brothers Friends In Low Places - Garth Brooks Fly Me To The Moon - Frank Sinatra Livin' On A Prayer - Bon Jovi Can't Stop The Feeling - Justin Timberlake Piano Man - Billy Joel I Want It That Way - Backstreet Boys All Of Me - John Legend Turn The Page - Bob Seger These Boots Are Made For Walkin' - Nancy Sinatra Can't Help Falling In Love - Elvis Presley My Way - Frank Sinatra (Sittin' On) The Dock Of The Bay - Otis Redding Folsom Prison Blues - Johnny Cash Me And Bobby McGee - Janis Joplin Love Shack - The B-52's 7 Years - Lukas Graham Wannabe - Spice Girls A Whole New World - -

Warner and Sony Set for Battle
01 15FEB Cover_v3_cover template 12/02/13 17:38 Page 1 07 9 776669 776136 THE BUSINESS OF MUSIC www.musicweek.com 15.02.13 £5.15 NEWS BIG INTERVIEW ANALYSIS 05 12 27 The legendary Sir George UK bosses Jason Iley and Mike Music Week talks to pop Martin accepts his MPG Smith discuss a promising year songwriting golden boy Outstanding Contribution Award ahead for the Universal label Wayne Hector Warner and Sony set for battle PARLOPHONE BUYOUT WILL DRAMATICALLY CLOSE THE GAP BETWEEN RIVAL MAJOR LABELS ANALYSIS market headed by Universal with I BY PAUL WILLIAMS a 35.0% share and Sony second with 20.8%. arner’s £487m buyout However, had Warner W of Parlophone Label controlled the artists and Group (PLG) will put repertoire coming from PLG in it within touching distance of 2011 and 2012 it would have Sony as Universal’s biggest rival claimed around 17.5% of the in the UK. albums market, just one and a That’s according to exclusive half percentage points behind Music Week research, which Sony, while it would have been suggests the addition of around the same distance behind repertoire from the likes of Sony on singles with a market Coldplay, David Guetta and Pink share of about 19.5%. Floyd will sharply narrow the On the albums side, the most market share race for second obvious powerful addition to its place. However, Universal could ranks will be Coldplay whose end up being 80% or more ahead Mylo Xyloto was EMI’s second of both rival players. -

I Am the Cat Who Walks by Himself
I am the cat who walks by himself Asher Peres∗ Abstract The city of lions. Beaulieu-sur-Dordogne. The war starts. Drˆole de guerre. Going to work. Going to school. Fleeing from village to village. Playing cat and mouse. The second landing. Return to Beaulieu. Return to Paris. Joining the boyscouts. Learning languages. Israel becomes independent. Arrival in Haifa. Kalay high school. Military training. The Hebrew Technion in Haifa. Relativity. Asher Peres. Metallurgy. Return to France. Escape from jail. Aviva. I am the cat who walks by himself, and all places are alike to me. Rudyard Kipling1 I am grateful to all those who contributed to this Festschrift which celebrates my 70th birthday and therefore the beginning of my eighth decade. In the Jewish religion, there is a prayer, “she-hehhyanu” to thank the Lord for having kept us alive and let us reach this day. I am an atheist and I have no Lord to thank, but I wish to thank many other people who are no longer alive and who helped me reach this point. The city of lions First, I thank my parents, Salomon and Salomea Pressman, for leaving Poland before World War II and going to live temporarily in France, so that we remained alive. Other- wise, I would not have been able to celebrate my seventh birthday. My family originated in a city which was called Lemberg when my parents were born in the Austrian empire, Lw´ow when I was born, Lviv (Ukraine) today. It also has a French name (L´eopol) and other names too. -

Presidential Documents
Weekly Compilation of Presidential Documents Monday, December 6, 1999 Volume 35ÐNumber 48 Pages 2453±2515 Contents Addresses and Remarks Bill Signings See also Bill Signings Consolidated appropriations legislation for FY California 2000 Democratic Congressional Campaign RemarksÐ2454 Committee luncheon in San FranciscoÐ StatementÐ2458 2469 Intelligence Authorization Act for Fiscal Year Southwest Voter Registration and 2000, statementÐ2512 Education Project reception in Beverly Veterans' Compensation Cost-of-Living HillsÐ2481 Adjustment Act of 1999, statementÐ2474 ``Stop the Violence'' benefit in Beverly Veterans Millennium Health Care and HillsÐ2474 Benefits Act, statementÐ2473 Economic growthÐ2508 Northern Ireland peace processÐ2500 Parental leaveÐ2466 Communications to Federal Agencies Pennsylvania, dinner for Mayor Rendell in PhiladelphiaÐ2506 Facilitating the Growth of Electronic Radio addressÐ2453 Commerce, memorandumÐ2457 Washington International Family Planning Waiver, International Labor Organization memorandumÐ2465 convention on the prohibition and elimination of the worst forms of child Executive Orders labor in Seattle, signingÐ2500 Washington State trade community in Amending Executive Order 10173, as SeattleÐ2489 Amended, Prescribing Regulations Relating World Trade Organization luncheon in to the Safeguarding of Vessels, Harbors, SeattleÐ2494 Ports, and Waterfront Facilities of the World AIDS Day, radio remarksÐ2499 United StatesÐ2500 (Continued on the inside of the back cover.) Editor's Note: The Weekly Compilation of Presidential Documents is also available on the Inter- net on the GPO Access service at http://www.gpo.gov/nara/nara003.html. WEEKLY COMPILATION OF regulations prescribed by the Administrative Committee of the Federal Register, approved by the President (37 FR 23607; 1 CFR Part 10). PRESIDENTIAL DOCUMENTS Distribution is made only by the Superintendent of Docu- ments, Government Printing Office, Washington, DC 20402.