Formation of Giant Globular Cluster G1 and the Origin of the M 31 Stellar Halo
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Most Massive Star Cluster in the Local Group
This is a repository copy of A 'super' star cluster grown old: the most massive star cluster in the Local Group. White Rose Research Online URL for this paper: http://eprints.whiterose.ac.uk/144713/ Version: Published Version Article: Ma, J., De Grijs, R., Yang, Y. et al. (5 more authors) (2006) A 'super' star cluster grown old: the most massive star cluster in the Local Group. Monthly Notices of the Royal Astronomical Society , 368 (3). pp. 1443-1450. ISSN 0035-8711 https://doi.org/10.1111/j.1365-2966.2006.10231.x This article has been accepted for publication in Monthly Notices of the Royal Astronomical Society © 2006 The Authors. Published by Oxford University Press on behalf of the Royal Astronomical Society. All rights reserved. Reuse Items deposited in White Rose Research Online are protected by copyright, with all rights reserved unless indicated otherwise. They may be downloaded and/or printed for private study, or other acts as permitted by national copyright laws. The publisher or other rights holders may allow further reproduction and re-use of the full text version. This is indicated by the licence information on the White Rose Research Online record for the item. Takedown If you consider content in White Rose Research Online to be in breach of UK law, please notify us by emailing [email protected] including the URL of the record and the reason for the withdrawal request. [email protected] https://eprints.whiterose.ac.uk/ Mon. Not. R. Astron. Soc. 368, 1443–1450 (2006) doi:10.1111/j.1365-2966.2006.10231.x A ‘super’ star cluster grown old: the most massive star cluster in the Local Group J. -

The Ellipticities of Globular Clusters in the Andromeda Galaxy
ASTRONOMY & ASTROPHYSICS MAY I 1996, PAGE 447 SUPPLEMENT SERIES Astron. Astrophys. Suppl. Ser. 116, 447-461 (1996) The ellipticities of globular clusters in the Andromeda galaxy A. Staneva1, N. Spassova2 and V. Golev1 1 Department of Astronomy, Faculty of Physics, St. Kliment Okhridski University of Sofia, 5 James Bourchier street, BG-1126 Sofia, Bulgaria 2 Institute of Astronomy, Bulgarian Academy of Sciences, 72 Tsarigradsko chauss´ee, BG-1784 Sofia, Bulgaria Received March 15; accepted October 4, 1995 Abstract. — The projected ellipticities and orientations of 173 globular clusters in the Andromeda galaxy have been determined by using isodensity contours and 2D Gaussian fitting techniques. A number of B plates taken with the 2 m Ritchey-Chretien-coud´e reflector of the Bulgarian National Astronomical Observatory were digitized and processed for each cluster. The derived ellipticities and orientations are presented in the form of a catalogue?. The projected ellipticities of M 31 GCs lie between 0.03 0.24 with mean valueε ¯=0.086 0.038. It may be concluded that the most globular clusters in the Andromeda galaxy÷ are quite spherical. The derived± orientations do not show a preference with respect to the center of M 31. Some correlations of the ellipticity with other clusters parameters are discussed. The ellipticities determined in this work are compared with those in other Local Group galaxies. Key words: globular clusters: general — galaxies: individual: M 31 — galaxies: star clusters — catalogs 1. Introduction Bergh & Morbey (1984), and Kontizas et al. (1989), have shown that the globulars in LMC are markedly more ellip- Representing the oldest of all stellar populations, the glo- tical than those in our Galaxy. -

Drilling Through the M31 Halo Near Mayall-II/G1
Drilling through the M31 Halo near Mayall-II/G1 Michael Gregg University of California, Davis Michael West Lowell Observatory Brian Lemaux University of California, Davis Andreas Küpper Quantco, Inc. Origin of the brightest Globulars Clusters Mayall-II/G1 in M31 Omega Cen in Milky Way •G1 has mass of ~107 M⊙ and σ = 25 km/s •High ellipticity, ~0.2, 50% rotationally supported •Metallicity spread, ~0.45 dex •Evidence for massive blackhole in the core, ~104 M⊙ •=> Former dwarf galaxy nucleus, now Ultra-Compact Dwarf? Origin of the brightest Globulars Clusters ...and connection to galaxy halo formation… HST image of nucleated Typical UCD (or bright globular) dwarf elliptical in in the same galaxy cluster: the Fornax galaxy cluster: possibly a tidally stripped nucleus nucleus + envelope of stars Origin of the brightest Globulars Clusters... Fornax Galaxy Cluster ...and connection to galaxy halo formation… image credit: M. Hilker •Evolved tidal streams are too faint (∼> 30 mag/sq.′′) to detect with standard imaging (Ibata et al. 2001; Ferguson et al. 2002; etc., etc., etc.) •Need resolved star spectroscopy to identify tidal debris; characteristics can perhaps can yield insight into the precursor of G1… G1 in Context Chemin et al. (2009) • We view G1 projected against the outer disk of M31, 2.6˚ (34 kpc) distant from the bulge. • The M31 disk has v < −500 km s-1 at G1 (Chemin et al. 2009). • G1 systemic v = −332 ± 3 km s-1 (Galleti et al. 2006), separation of ∼ 170 km s-1, 5-6 times the velocity dispersion of G1 or the M31 cold disk. -

Mayall II= G1 in M31: Giant Globular Cluster Or Core of a Dwarf Elliptical
Mayall II ≡ G1 in M31: Giant Globular Cluster or Core of a Dwarf Elliptical Galaxy? 1,2 G. Meylan3 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, U.S.A., email: [email protected], and European Southern Observatory, Karl-Schwarzschild-Str. 2, D-85748 Garching bei M¨unchen, Germany. A. Sarajedini University of Florida, Astronomy Department, Gainesville, FL 32611-2055, U.S.A. email: [email protected]fl.edu P. Jablonka DAEC-URA 8631, Observatoire de Paris-Meudon, Place Jules Janssen, F-92195 Meudon, France. email: [email protected] S. G. Djorgovski Palomar Observatory, MS 105–24, Caltech, Pasadena, CA 91125, U.S.A. email: [email protected] T. Bridges Anglo-Australian Observatory, PO Box 296, Epping, NSW 2121, Australia. email: [email protected] R. M. Rich UCLA, Physics & Astronomy Department, Math-Sciences 8979, Los Angeles, CA 90095-1562, U.S.A. email: [email protected] 1 Based in part on observations made with the NASA/ESA Hubble Space Telescope, obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-26555. These observations are associate with proposal IDs 5907 and 5464. arXiv:astro-ph/0105013v1 1 May 2001 2 Based in part on observations obtained at the W.M. Keck Observatory, which is operated jointly by the California Institute of Technology and the University of California. 3 Affiliated with the Astrophysics Division of the European Space Agency, ESTEC, Noordwijk, The Netherlands. ABSTRACT Mayall II ≡ G1 is one of the brightest globular clusters belonging to M31, the Andromeda galaxy. -

The 2011 Observers Challenge List
TMSP OBSERVER'S CHALLENGE 2011 By Kreig McBride and Tom Masterson All observations must be made at TMSP and 25 out of 30 objects must be viewed to earn a unique TMSP Observer's Award lapel pin. You must create a record of your observations which include date, time, instruments used and a brief description and/or sketch of the object. Your records will be returned to you. Size or ID Number V Magnitude Object Type Constellation RA Dec Description Separation The Sun! View 2 days noting changes. H-alpha, white 1 Sol -28m ½ degree Star Cancer 08h 39' +27d 07' light or projection is OK North Galactic Astronomical Catch this one before it sets. Next to the double star 31 2 N/A N/A Coma Berenices 12h 51' +27d 07' Pole Reference point Comae Berenices Omicron-2 a wide 4.9m, 9m double lies close by as does 3 U Cygni 5.9 – 12.1m N/A Carbon Star Cygnus 19.6h +47d 54' 6” diameter, 12.6m Planetary nebula NGC6884 4 M22 5.1m 7.8' Globular Cluster Sagittarius 18h 36.4' -23d 54' Rich, large and bright 5 NGC 6629 11.3m 15” Planetary Nebula Sagittarius 18h 25.7' -23d 12' Stellar at low powers. Central Star is 12.8m 6 Barnard 86 N/A 5' Dark Nebula Sagittarius 18h 03' -27d 53' “Ink Spot” Imbedded in spectacular star field Faint 1' glow surrounding 9.5m star w/a faint companion 7 NGC 6589-90 N/A 5' x 3' Reflection Nebula Sagittarius 18h 16.9'' -19d 47' 25” to its SW A 3.2m, B Reddish/Orange primary, B white, C is 10m companion 8 ETA Sagittarii 3.6m, C 10m, AB pair 3.6” Quadruple Star Sagittarius 18h 17.6' -36d 46' 93” distant at PA303d and D is 13m star 33” -

Globular Cluster Club
Globular Cluster Observing Club Raleigh Astronomy Club Version 1.2 22 June 2007 Introduction Welcome to the Globular Cluster Observing Club! This list is intended to give you an appreciation for the deep-sky objects known as globular clusters. There are 153 known Milky Way Globular Clusters of which the entire list can be found on the seds.org site listed below. To receive your Gold level we will only have you do sixty of them along with one challenge object from a list of three. Challenge objects being the extra-galactic globular Mayall II (G1) located in the Andromeda Galaxy, Palomar 4 in Ursa Major, and Omega Centauri a magnificent southern globular. The first two challenge your scope and viewing ability while Omega Centauri challenges your ability to plan for a southern view. A Silver level is also available and will be within the range of a 4 inch to 8 inch scope depending upon seeing conditions. Many of the objects are found in the Messier, Caldwell, or Herschel catalogs and can springboard you into those clubs. The list is meant for your viewing enrichment and edification of these types of clusters. It is also meant to enhance your viewing skills. You are encouraged to view the clusters with a critical eye toward the cluster’s size, visual magnitude, resolvability, concentration and colors. The Astronomical League’s Globular Clusters Club book “Guide to the Globular Cluster Observing Club” is an excellent resource for this endeavor. You will be asked to either sketch the cluster or give a short description of your visual impression, citing seeing conditions, time, date, cluster’s size, magnitude, resolvability, concentration, and any star colors. -

54-4 Fall 2017
The Valley Skywatcher Official Publication of the Chagrin Valley Astronomical Society PO Box 11, Chagrin Falls, OH 44022 www.chagrinvalleyastronomy.org Founded 1963 Contents CVAS Officers Articles President Marty Mullet “Seeing” an Extragalactic Globular Cluster 2 Vice President Ian Cooper Regular Features Treasurer Steve Fishman Astrophotography 4 Secretary Christina Gibbons President’s Corner 13 Director of Observations Steve Kainec Observer’s Log 14 Book Review 16 Observatory Director Robb Adams Constellation Quiz 17 Historian Dan Rothstein Notes & News 19 Editor Ron Baker Reflections 19 Author’s Index, Volume 54 20 Two panel mosaic of Messier 82 and Messier 81. 20-inch f/6.8 Corrected Dall-Kirkham telescope. Assembled with Photoshop Elements 11. Processed in Photoshop CS2 and Topaz Adjust. Image by CVAS Member David Mihalic. The Valley Skywatcher • Fall 2017 • Volume 54-4 • Page 1 “Seeing” an Extragalactic Globular Cluster By Russ Swaney At Star Parties we know the Moon, planets, and bright double stars are always attention getters. But I like the im- pression globular star clusters leave on first-time stargazers. The visual impact of Saturn or Jupiter is immediate, but with globular clusters there is this delay in recognizing what you’re looking at and then truly seeing it and then “Look at all those STARS!” I’m sure you’ve all had the opportunity to observe globular clusters in our Milky Way Galaxy (M13, M5, M3, M15 etc.), but have you ever considered looking for one in ANOTHER GALAXY? Yes, they are very far away and even the brightest is less than 12 magnitude. So why spend time searching for some- thing that pretty much just looks like another star field? In my case it’s the challenge of seeing something like M13 but immensely further away. -

In This Issue
Southern Skies Volume 24, Number 3 Journal of the Southeastern Planetarium Association Summer 2004 In This Issue President’s Message ...................................................................................................................... 1 IPS Report ....................................................................................................................................... 2 Editor’s Message: Deadlines and Guidelines .............................................................................. 3 SEPA Membership Form ................................................................................................................ 3 Small Talk ........................................................................................................................................ 4 Astro Video Review: Our Amazing Solar System ........................................................................ 5 Featured Facility: Calusa Nature Center and Planetarium, Fort Meyers, Florida ..................... 6 Digital Cosmos: Celestia ................................................................................................................ 8 News from SEPA States ............................................................................................................... 10 HST’s Greatest Hits of ’96 Slides ................................................................................................ 14 HST’s Greatest Hits of ’97 Slides ............................................................................................... -

Download (10MB)
METEOR CSILLAGÁSZATI ÉVKÖNYV 2020 meteor csillagászati évkönyv 2020 Szerkesztette: Benkő József Mizser Attila Magyar Csillagászati Egyesület www.mcse.hu Budapest, 2019 Az évkönyv kalendárium részének összeállításában közreműködött: Bagó Balázs Görgei Zoltán Kaposvári Zoltán Kovács József Molnár Péter Sánta Gábor Sárneczky Krisztián Szabadi Péter Szabó Sándor Szőllősi Attila Zsoldos Endre A kalendárium csillagtérképei az Ursa Minor szoftverrel készültek. www.ursaminor.hu Szakmailag ellenőrizte: Szabados László A kiadvány támogatói: A kiadvány a Magyar Tudományos Akadémia támogatásával készült. További támogatók: mindazok, akik az SZJA 1%-ával támogatják a Magyar Csillagászati Egyesületet Adószámunk: 19009162-2-43 Felelős kiadó: Mizser Attila Nyomdai előkészítés: Molnár Péterné Nyomtatás, kötészet: Gelbert Eco Print Terjedelem: 20,5 ív fekete-fehér + 8 oldal színes melléklet 2019. november ISSN 0866-2851 Tartalom Bevezető ....................................................................................................... 7 Kalendárium .............................................................................................. 13 Cikkek Hegedüs Tibor: Égi kövek nyomában .......................................................175 Plachy Emese – Molnár László: Ég veled, Kepler! ......................................197 Könyves-Tóth Réka, Vinkó József, Stermeczky Zsófi a: Tranziens jelenségek az égbolton .........................................................230 Horváth István: A Shapley–Curtis-vita ................................................... -

Mayall II ≡ G1 in M31: Giant Globular Cluster Or Core of a Dwarf Elliptical Galaxy?
Mayall II G1 in M31: ≡ Giant Globular Cluster or Core of a Dwarf Elliptical Galaxy? 1;2 G. Meylan3 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, U.S.A., email: [email protected], and European Southern Observatory, Karl-Schwarzschild-Str. 2, D-85748 Garching bei M¨unchen, Germany. A. Sarajedini University of Florida, Astronomy Department, Gainesville, FL 32611-2055, U.S.A. email: [email protected]fl.edu P. Jablonka DAEC-URA 8631, Observatoire de Paris-Meudon, Place Jules Janssen, F-92195 Meudon, France. email: [email protected] S. G. Djorgovski Palomar Observatory, MS 105–24, Caltech, Pasadena, CA 91125, U.S.A. email: [email protected] T. Bridges Anglo-Australian Observatory, PO Box 296, Epping, NSW 2121, Australia. email: [email protected] R. M. Rich UCLA, Physics & Astronomy Department, Math-Sciences 8979, Los Angeles, CA 90095-1562, U.S.A. email: [email protected] 1 Based in part on observations made with the NASA/ESA Hubble Space Telescope, obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-26555. These observations are associate with proposal IDs 5907 and 5464. 2 Based in part on observations obtained at the W.M. Keck Observatory, which is operated jointly by the California Institute of Technology and the University of California. 3 Affiliated with the Astrophysics Division of the European Space Agency, ESTEC, Noordwijk, The Netherlands. ABSTRACT Mayall II G1 is one of the brightest globular clusters belonging to M31, the Andromeda ≡ galaxy. -

Deep HST V- and I-Band Observations of the Halo Of
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by CERN Document Server accepted for publication in the AJ Deep HST V-andI-Band Observations of the Halo of M31: Evidence for Multiple Stellar Populations1 Stephen Holland, Gregory G. Fahlman, & Harvey B. Richer Department of Physics & Astronomy #129–2219 Main Mall University of British Columbia Vancouver, B.C., Canada V6T 1Z4 ABSTRACT We present deep (V ' 27) V-andI-band stellar photometry obtained using the Hubble Space Telescope’s WFPC2 in two fields in the M31 halo. These fields are located 320 and 500 from the center of M31 approximately along the SE minor axis at the locations of the M31 globular star clusters G302 and G312 respectively. The M31 halo luminosity functions are not consistent with a single high-metallicity population but are consistent with a mix of 50% to 75% metal-rich stars and 25% to 50% metal-poor stars. This is consistent with the observed red giant branch morphology, the luminosity of the horizontal branch, and the presence of RR Lyrae stars in the halo of M31. The morphology of the red giant branch indicates a spread in metallicity of −2 ∼< [m/H] ∼< −0.2 with the majority of stars having [m/H] '−0.6, making the halo of M31 significantly more metal-rich than either the Galactic halo or the M31 globular cluster system. The horizontal branch is dominated by a red clump similar to the horizontal branch of the metal-rich Galactic globular cluster 47 Tuc but a small number of blue horizontal branch stars are visible, supporting the conclusion that there is a metal-poor component to the stellar population of the halo of M31. -
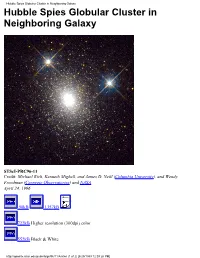
Hubble Spies Globular Cluster in Neighboring Galaxy Hubble Spies Globular Cluster in Neighboring Galaxy
Hubble Spies Globular Cluster in Neighboring Galaxy Hubble Spies Globular Cluster in Neighboring Galaxy STScI-PRC96-11 Credit: Michael Rich, Kenneth Mighell, and James D. Neill (Columbia University), and Wendy Freedman (Carnegie Observatories) and NASA April 24, 1996 90kB 1357kB 722kB Higher resolution (300dpi) color 552kB Black & White http://oposite.stsci.edu/pubinfo/pr/96/11/A.html (1 of 2) [5/25/1999 12:09:26 PM] Hubble Spies Globular Cluster in Neighboring Galaxy Hubble Space Telescope has captured a view of a globular cluster called G1, a large, bright ball of light in the center of the photograph consisting of at least 300,000 old stars. G1, also known as Mayall II, orbits the Andromeda galaxy (M31), the nearest major spiral galaxy to our Milky Way. Located 130,000 light-years from Andromeda's nucleus, G1 is the brightest globular cluster in the Local Group of galaxies. The Local Group consists of about 20 nearby galaxies, including the Milky Way. The crisp image is comparable to ground-based telescope views of similar clusters orbiting the Milky Way. The Andromeda cluster, however, is nearly 100 times farther away. A glimpse into the cluster's finer details allow astronomers to see its fainter helium-burning stars whose temperatures and brightnesses show that this cluster in Andromeda and the oldest Milky Way clusters have approximately the same age. These clusters probably were formed shortly after the beginning of the universe, providing astronomers with a record of the earliest era of galaxy formation. During the next two years, astronomers will use Hubble to study about 20 more globular clusters in Andromeda.