PM2.5 Cooperative Control with Fuzzy Cost and Fuzzy Coalitions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Download Article (PDF)
International Conference on Educational Research and Sports Education (ERSE 2013) The Physical Education Teaching in Colleges from the Perspective of Lifelong Sports Sun Fenglin Department of Physical Education , Beijing WuZi University, Beijing, China [email protected] Abstract - This article discusses the necessity of combining A. Theory of Motivation education and lifelong physical education in colleges, and sets out Motivation refers to the psychological motivations or the theoretical basis of the connection between the physical education in colleges and lifelong physical education. Based on that, the paper internal driving forces to promote personal activities. We can also analyzes the problems on teaching philosophy, curriculum, classify motivations according to the features of interest: (1) evaluation of teaching and teaching methods of college sports. In direct motivation: it refers to the activity itself, taking direct addition, some detailed suggestions are put forward for improvement. interest as the foundation. (2) indirect motivation: it refers to Index Terms - Physical education, lifelong sports, curriculum, the result based on the indirect interest. For example, if a evaluation person loves to play basketball, and can get fun from it, this is because he is driven by the direct motivation, while a twelve- 1. Introduction minute running test is mostly caused by indirect motivation. A With the quickening pace of China’s socialist person is often influenced by the direct motivation. General modernization, people’s living standard has greatly improved. physical activity is driven by these two kinds of motivation. However, the physical conditions of college students in China The body need is an unbalanced state, which reflects the are on a descending trend, and college students do not pay necessity and some objective requirements. -

The Co-Cultivation Program"
2017 4th International Conference on Advanced Education Technology and Management Science (AETMS 2017) ISBN: 978-1-60595-489-9 Analysis on the Problems and Solutions of Implementing "The Co-cultivation Program" Jian GUO*, Li ZHOU and Jie ZHU School of information, Beijing Wuzi University, Beijing, China *Corresponding author Keywords: Co-cultivation program, Co-cultivation students, Talents cultivation. Abstract. The Beijing Municipal Education Commission began to implement "the co-cultivation program" since 2015. Beijing Wuzi University as one of Beijing municipal universities taking part in this program explore actively the training mode of co-cultivation students, cultivating grogram, curriculum system, student management, establishment of virtual teaching and researching office and other aspects with its counterparts universities under the Ministry of Education directly. The project is implemented firstly in Beijing and even in the whole country, and there are still some problems in the actual implementation. Therefore, it is necessary to explore how to ensure the smooth implementation of the project. This paper analyzes the significance of the implementation of this project to our school, sorts out the problems in the development of the "the co-cultivation program" in our university, and puts forward some corresponding countermeasures, which will play an important role in the better implementation of the project in our school, and it also will be of reference significance for other brothers colleges to carry out this project better. Introduction The "national long-term education reform and development plan (2010-2020)" clearly puts forward that the reform and innovation should be a powerful driving force in the development of education. -

A Complete Collection of Chinese Institutes and Universities For
Study in China——All China Universities All China Universities 2019.12 Please download WeChat app and follow our official account (scan QR code below or add WeChat ID: A15810086985), to start your application journey. Study in China——All China Universities Anhui 安徽 【www.studyinanhui.com】 1. Anhui University 安徽大学 http://ahu.admissions.cn 2. University of Science and Technology of China 中国科学技术大学 http://ustc.admissions.cn 3. Hefei University of Technology 合肥工业大学 http://hfut.admissions.cn 4. Anhui University of Technology 安徽工业大学 http://ahut.admissions.cn 5. Anhui University of Science and Technology 安徽理工大学 http://aust.admissions.cn 6. Anhui Engineering University 安徽工程大学 http://ahpu.admissions.cn 7. Anhui Agricultural University 安徽农业大学 http://ahau.admissions.cn 8. Anhui Medical University 安徽医科大学 http://ahmu.admissions.cn 9. Bengbu Medical College 蚌埠医学院 http://bbmc.admissions.cn 10. Wannan Medical College 皖南医学院 http://wnmc.admissions.cn 11. Anhui University of Chinese Medicine 安徽中医药大学 http://ahtcm.admissions.cn 12. Anhui Normal University 安徽师范大学 http://ahnu.admissions.cn 13. Fuyang Normal University 阜阳师范大学 http://fynu.admissions.cn 14. Anqing Teachers College 安庆师范大学 http://aqtc.admissions.cn 15. Huaibei Normal University 淮北师范大学 http://chnu.admissions.cn Please download WeChat app and follow our official account (scan QR code below or add WeChat ID: A15810086985), to start your application journey. Study in China——All China Universities 16. Huangshan University 黄山学院 http://hsu.admissions.cn 17. Western Anhui University 皖西学院 http://wxc.admissions.cn 18. Chuzhou University 滁州学院 http://chzu.admissions.cn 19. Anhui University of Finance & Economics 安徽财经大学 http://aufe.admissions.cn 20. Suzhou University 宿州学院 http://ahszu.admissions.cn 21. -

CAER Leaflet.Qxd
Editor:Professor Xian Xin ISSN 1756-137X Volume 1 Number1 2008 Review process:Double blind peer review China Agricultural Economic Review Established:First issue launching Autumn 2008 Frequency:4 issues per year Published in association with ISSN:1756-137X Volume:1, 2008 www.emeraldinsight.com ER China Agricultural Economic Review Following China’s accession to the World Trade Organization, the Chinese economy has become increasingly integrated into the world economy. In A particular Chinese agricultural development experiences and research have much to offer for readers world-wide. Launching its first issue in Autumn 2008,China Agricultural Economic Review (CAER) will provide a unique and insightful approach to documenting and disseminating research into the economics of agriculture, natural resources and the environment, and rural development. The journal seeks to address contemporary issues concerning agricultural economics C and rural development in China, thus having an impact on China’s agricultural and rural policy-making processes and also on the development of the agricultural economics discipline. Published in association with The world’s leading publisher of management research www.emeraldinsight.com/caer.htm ABOUT THE EDITOR COVERAGE INCLUDES: Professor Xian Xin is • Agricultural economic theory and policy Deputy Dean of the • Agricultural markets College of Economics and • Agricultural trade Management and Deputy • Agricultural investment Director of the Center for Rural Development Policy • Rural finance at the China Agricultural • Resource economics and environment protection University. He has • Agricultural R&D and extension published six books and • Employment, labour use and migration over 40 articles on China’s agricultural and • Agribusiness rural development issues • Rural sociology and international trade. -

University of Leeds Chinese Accepted Institution List 2021
University of Leeds Chinese accepted Institution List 2021 This list applies to courses in: All Engineering and Computing courses School of Mathematics School of Education School of Politics and International Studies School of Sociology and Social Policy GPA Requirements 2:1 = 75-85% 2:2 = 70-80% Please visit https://courses.leeds.ac.uk to find out which courses require a 2:1 and a 2:2. Please note: This document is to be used as a guide only. Final decisions will be made by the University of Leeds admissions teams. -

Call for Papers Academician JIANG Zhuangde Xi’An Jiaotong Date:Oct
The 12th Annual Conference of China Venue: Beijing, China 3. Business Model Innovation and Enterprise Industrial Technology Association of Strategy Transformation in homogenization Economics & Management Institutes and Websites: time http://www.bjtu.edu.cn The First International Conference on http://www.lanshanwenhua.com Honorary Chairman: Management, Innovation& Development http://www.seiofbluemountain.com Academician XU Shoubo Beijing Jiaotong (MID2014) http://www.meeting.edu.cn University; Call for Papers Academician JIANG Zhuangde Xi’an Jiaotong Date:Oct. 25 - 26 2014 University; Symposium Theme: Chairman of Symposium: Strategic Management InnovationProf. ZHANG and Business Mingyu, Pro. ZHANG Mingyu Beijing Jiaotong Model Reengineering University; Prof. ZENG Xiaochun Xi’an Jiaotong Topics referenced: Strategic Management, Corporate Governance, University; Sponsors: Commercial Model Innovation, Enterprise Prof. ZHAO Ruimei China University of China Industrial Technology Association of Competitiveness, Brand Strategy, Financial Geosciences (Beijing) Economic & Management Institutes Strategy, Marketing Strategy, Strategic Human Resources, Transportation Organization and Program President: Organizers: Management, Enterprise Resource Planning, Prof. ZHANG Wensong Beijing Jiaotong School of Economics and Management, Beijing Electronics Business, Technology Management, University Jiaotong University; Entrepreneurial Management, Culture Industry Eastern Academic Forum (Australia); and New Media, Tourism Strategy and Academic Committee: Management, -

A Topology Adjustment Algorithm for P2P Systems
JOURNAL OF SOFTWARE, VOL. 9, NO. 8, AUGUST 2014 2217 A Topology Adjustment Algorithm for P2P Systems Zhen Yu, Jie Zhu, Guicheng Shen School of Information, Beijing Wuzi University, Beijing, China Email: [email protected] Haiyan Liu State Key Laboratory of Hydroscience and Engineering, Tsinghua University, Beijing, China Email: [email protected] Abstract—In order to improve the Peer-to-Peer (P2P) the topology is adjusted by the credibility of peers, but the network resource locating efficiency and isolate malicious calculation of abilities of neighbors is one-sided, and fails peers, a topology adjustment algorithm for unstructured to adjust to the fairness of topology. To improve the P2P networks is proposed. TTL (time-to-live) value for each efficiency of resource orientation, and isolate malicious neighbor has been set up and adjusted; specific information on the query path is recorded; a topology adjustment peers, this paper presents a topology adjustment algorithm algorithm is given. The topology adjustment algorithm is for unstructured P2P networks, and the effectiveness of evaluated by peer shortest path, simulation and analysis topology has been verified based on the shortest path. show that the topology adjustment algorithm can isolate Simulation and analysis show the effectiveness of the malicious peers to the network edge, and improve service algorithm. quality of P2P networks. The rest of this paper is organized as follows: section Ⅱ discusses related work. Section Ⅲ introduces our Index Terms—Peer-to-Peer; unstructured; topology; approach to record forwarding information of the shortest path algorithm. Section Ⅳ gives detailed explanations and analyses of the topology adjustment algorithm. Section I. -

An Empirical Research on Flipped Classroom Video-Making Based on Learners’ Demand Analysis
Journal of US-China Public Administration, April 2016, Vol. 13, No. 4, 271-277 doi: 10.17265/1548-6591/2016.04.006 D DAVID PUBLISHING An Empirical Research on Flipped Classroom Video-Making Based on Learners’ Demand Analysis Ling Zhang Beijing Wuzi University, Beijing, China With the development of online education and mobile learning, micro-video has become a common learning resource, how to improve the quality of the video has become a hot issue. In this paper, a questionnaire was launched to analyze different styles of micro-class videos and students’ requirement on videos, based on which the micro-class video-making principles are further analyzed in order to find out an easy video-production method which can be independently operated by college teachers. Moreover, a sample video is produced according to the video-making methods, and an empirical comparative study is done to analyze the learning outcome differences based on the video we made and the video from the internet. The results reveal that students are positive to micro-video which is made on the video-making principles and students obtained a better learning outcome by learning through this video. In the last part, this paper summarized advantages and limitations of the experiment, and provided suggestions on how to implement a more effective and low-cost way to make micro-class videos. Keywords: demand analysis, video-making, flipped classroom The development of online video and mobile technology has realized miniaturized and fragmented study and provided a new path for lifelong learning, as well as teacher’s professional development, even classroom teaching. -

History of Chung-Ang University
Open Your Future @CAU in Seoul, Korea Contact Us Office of International Affairs 84 Heukseok-ro, Dongjak-gu, Seoul 06974, Korea Tel: 82-2-820-6202, 6570, 6574, 6744 Fax: 82-2-813-8069 Email: [email protected] http://oia.cau.ac.kr Contents 04 l Korea and Seoul 05 l Campuses 06 l History of Chung-Ang University A leading private comprehensive university established in 1918 08 l About CAU l Campuses : Seoul and Anseong 10 Study Abroad and Exchange Program 12 l Cultural Activities Korean conglomerate Doosan incorporated CAU in 2008 13 l CAU Global Ambassadors 14 l International Summer / Winter Program 16 l Customized Study Tour Program 18 l Blue Mir Hall (Dormitory) 19 l International Partners 22 l Fields of Study 13 18 23,453 Colleges Graduate Programs Undergraduate Students 8,273 2,331 2,820 645 Graduate Students International Students Professors Administrators Campuses Campuses Dobong Nowon -gu -gu History of Chung-Ang Gangbuk University -gu Eunpyeong Jongno -gu -gu About CAU Seongbuk Jungnang -gu -gu Seodae Dongdae mun-gu Mapo-gu Seoul Tower mun-gu Incheon Int’l Gimpo Int’l Seoul Airport Airport Worl’d Cup Jung-gu Seong Stadium Dobong Nowon dong-gu Gangseo-gu -gu -gu Gangdong-gu Gwangjin Gangbuk -gu -gu Seoul Station Eunpyeong Jongno -gu -gu 63 BuildingSeongbuk Jungnang Yongsan-gu Yangcheon -gu -gu Seodae Dongdae Gangnam mun-gu Yeong Mapo-gu-gu Seoul Tower mun-gu -gu Incheon Int’l Gimpo Int’l Seoul deung Dong Airport Airport Worl’d Cup Jung-gu Seong Stadium po-gudong-gu jak-gu Gangseo-gu Gangdong-gu Songpa-gu Republic of KOREA Gwangjin Guro-gu Seoul Station -gu COEX 63 Building Yongsan-gu Chung-Ang Yangcheon Gangnam -gu Yeong deung Dong -gu po-gu jak-gu Songpa-guUniv. -
1 Please Read These Instructions Carefully
PLEASE READ THESE INSTRUCTIONS CAREFULLY. MISTAKES IN YOUR CSC APPLICATION COULD LEAD TO YOUR APPLICATION BEING REJECTED. Visit http://studyinchina.csc.edu.cn/#/login to CREATE AN ACCOUNT. • The online application works best with Firefox or Internet Explorer (11.0). Menu selection functions may not work with other browsers. • The online application is only available in Chinese and English. 1 • Please read this page carefully before clicking on the “Application online” tab to start your application. 2 • The Program Category is Type B. • The Agency No. matches the university you will be attending. See Appendix A for a list of the Chinese university agency numbers. • Use the + by each section to expand on that section of the form. 3 • Fill out your personal information accurately. o Make sure to have a valid passport at the time of your application. o Use the name and date of birth that are on your passport. Use the name on your passport for all correspondences with the CLIC office or Chinese institutions. o List Canadian as your Nationality, even if you have dual citizenship. Only Canadian citizens are eligible for CLIC support. o Enter the mailing address for where you want your admission documents to be sent under Permanent Address. Leave Current Address blank. Contact your home or host university coordinator to find out when you will receive your admission documents. Contact information for you home university CLIC liaison can be found here: http://clicstudyinchina.com/contact-us/ 4 • Fill out your Education and Employment History accurately. o For Highest Education enter your current degree studies. -

2019 Tsinghua International Econometrics Conference WELCOME
2019 Tsinghua International Econometrics Conference Conference Booklet 22-23 June, 2019 School of Economics and Management, Tsinghua University Beijing, China 2019 Tsinghua International Econometrics Conference WELCOME From the Local Organizing Committee The Local Organizing Committee warmly welcomes you to this year’s conference at Tsinghua University, and wishes you a fruitful and enjoyable stay. Organizing Committee: Chair: Chong-En Bai (Department of Economics, Tsinghua University) Co-chairs: Liangjun Su (School of Economics, Singapore Management University) Shengjie Hong (Department of Economics, Tsinghua University) Committee members: (in alphabetical order of last name) Yubo Chen (Department of Marketing, Tsinghua University) Sainan Jin (School of Economics, Singapore Management University) Qi Li (Department of Economics, Texas A&M University) Taoxiong Liu (Institute of Economics, Tsinghua University) Wenqing Pan (Department of Economics, Tsinghua University) Ke Tang (Institute of Economics, Tsinghua University) Xiaohan Zhong (Department of Economics, Tsinghua University) Lin Zhu (Department of Economics, Tsinghua University) Administrative staff and students: Yu Wang Xin Tian Yi Li Yinong Tan Zechao Li (If you need any assistant during the conference, please feel free to contact Yu Wang at (86) 15910606359, or Yi Li at (86) 13021254832.) 2019 Tsinghua International Econometrics Conference Contents Page Contents 2 Acknowledgements 3 About the National Institute for Fiscal Studies 4 Keynote Speaker 6 Program 9 Presentation Information 24 List of Participants 25 Notes 1 2019 Tsinghua International Econometrics Conference Acknowledgements We would like to express our sincerest gratitude to the School of Economics & Management (SEM) at Tsinghua University for providing us an opportunity to host the 2019 International Econometrics Conference. In particular, we deeply thank the National Institute for Fiscal Studies for providing the financial support. -
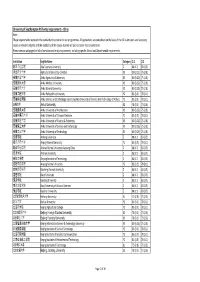
University of Southampton PGT Entry Requirements ‐ China Note: These Requirements Represent the Standard Entry Criteria for Our Programmes
University of Southampton PGT entry requirements ‐ China Note: These requirements represent the standard entry criteria for our programmes. All applications are considered on the basis of the full submission, and so strong scores in relevant subjects and the suitability of the course studied will also be taken into consideration. Please see our webpages for full information and entry requirements, including specific School and Departmental requirements. Institution English Name Category 2:1 2:2 阿坝师范学院 Aba Teachers University Z 88 (3.7) 83 (3.5) 河北农业大学 Agricultural University of Hebei X3 80 (3.25) 75 (2.8) 安徽农业大学 Anhui Agricultural University X3 80 (3.25) 75 (2.8) 安徽医科大学 Anhui Medical University X3 80 (3.25) 75 (2.8) 安徽师范大学 Anhui Normal University X3 80 (3.25) 75 (2.8) 安徽工程大学 Anhui Polytechnic University Y2 83 (3.5) 78 (3.1) 安徽科技学院 Anhui Science and Technology University (AKA University of Science And Technology of Anhui) Y2 83 (3.5) 78 (3.1) 安徽大学 Anhui University X2 78 (3.1) 73 (2.6) 安徽建筑大学 Anhui University of Architecture X3 80 (3.25) 75 (2.8) 安徽中医药大学 Anhui University of Chinese Medicine Y2 83 (3.5) 78 (3.1) 安徽财经大学 Anhui University of Finance & Economics X3 80 (3.25) 75 (2.8) 安徽理工大学 Anhui University of Science and Technology X3 80 (3.25) 75 (2.8) 安徽工业大学 Anhui University of Technology X3 80 (3.25) 75 (2.8) 安康学院 Ankang University Z 88 (3.7) 83 (3.5) 安庆师范大学 Anqing Normal University Y2 83 (3.5) 78 (3.1) 鞍山师范学院 Anshan Normal University Liaoning China Z 88 (3.7) 83 (3.5) 安顺学院 Anshun University Z 88 (3.7) 83 (3.5) 安阳工学院 Anyang Institute of Technology