Rothamsted Repository Download
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

IB Process Plant Study Page 2 of 107
Industrial Biotechnology Process Plant Study March 2015 A report for: The Biotechnology and Biological Sciences Research Council (BBSRC), The Engineering and Physical Sciences Research Council (EPSRC), Innovate UK and The Industrial Biotechnology Leadership Forum (IBLF). Authors: David Turley1, Adrian Higson1, Michael Goldsworthy1, Steve Martin2, David Hough2, Davide De Maio1 1 NNFCC 2 Inspire Biotech Approval for release: Adrian Higson Disclaimer While NNFCC and Inspire biotech considers that the information and opinions given in this work are sound, all parties must rely on their own skill and judgement when making use of it. NNFCC will not assume any liability to anyone for any loss or damage arising out of the provision of this report. NNFCC NNFCC is a leading international consultancy with expertise on the conversion of biomass to bioenergy, biofuels and bio-based products. NNFCC, Biocentre, Phone: +44 (0)1904 435182 York Science Park, Fax: +44 (0)1904 435345 Innovation Way, E: [email protected] Heslington, York, Web: www.nnfcc.co.uk YO10 5DG. IB Process Plant Study Page 2 of 107 Acknowledgement NNFCC wishes to acknowledge the input of the many stakeholders who provided information on the pilot scale equipment present in their respective facilities and more specifically the following stakeholders who gave of their time and experience, either in the workshop, or in one-to-one discussions with the project team. We would like to thank all for their valued input. Sohail Ali Plymouth Marine Laboratory Mike Allen Plymouth Marine Laboratory -

Long-Term Experiments
ROTHAMSTED LONG-TERM EXPERIMENTS Guide to the Classical and other Long-term experiments, Datasets and Sample Archive Edited by A. J. Macdonald Contributors Andy Macdonald, Paul Poulton, Ian Clark, Tony Scott, Margaret Glendining, Sarah Perryman, Jonathan Storkey, James Bell, Ian Shield, Vanessa McMillan and Jane Hawkins. Rothamsted Research Harpenden, Herts, AL5 2JQ, UK Tel +44 (0) 1582 763133 Fax +44 (0) 1582 760981 www.rothamsted.ac.uk 1 CONTENTS INTRODUCTION 4 THE CLASSICAL EXPERIMENTS 7 Broadbalk Winter Wheat 7 Broadbalk and Geescroft Wildernesses 19 Park Grass 20 Hoosfield Spring Barley 31 Exhaustion Land 34 Garden Clover 36 OTHER LONG-TERM EXPERIMENTS 37 At Rothamsted 37 At Woburn 39 RESERVED AND DISCONTINUED EXPERIMENTS 41 Barnfield 41 Hoosfield Alternate Wheat and Fallow 41 Woburn Market Garden 42 Agdell 42 The Woburn Intensive Cereals Experiments 43 Saxmundham, Rotations I & II 43 Amounts of Straw and Continuous Maize Experiments 44 (Rothamsted and Woburn) METEOROLOGICAL DATA 45 LONG-TERM EXPERIMENTS AS A RESOURCE 45 THE ROTHAMSTED SAMPLE ARCHIVE 47 ELECTRONIC ROTHAMSTED ARCHIVE (e-RA) 49 THE ROTHAMSTED INSECT SURVEY (RIS) 50 UK ENVIRONMENTAL CHANGE NETWORK (ECN) 52 NORTH WYKE FARM PLATFORM 53 MAP OF ROTHAMSTED FARM 28 REFERENCES 56 The Rothamsted Long-term Experiments are supported by the UK Biotechnology and Biological Sciences Research Council Front cover under the National Capabilities programme Broadbalk from the air, 2015 2018 © Rothamsted Research grant (BBS/E/C/000J0300), and by the Back cover ISBN 978-1-9996750-0-4 (Print) Lawes Agricultural Trust. Park Grass from the air, 2015 ISBN 978-1-9996750-1-1 (Online) 2 FOREWORD It is a testament to the foresight and Managing and documenting these experiments commitment of Sir John Lawes and Sir Henry and their associated data and archives is Gilbert, as well as others who have come after not a trivial task. -

Revised Edition 2019 ACKNOWLEDGEMENTS
Revised Edition 2019 ACKNOWLEDGEMENTS Written and researched by: Ian Fitzpatrick, Richard Young and Robert Barbour with Megan Perry, Emma Rose and Aron Marshall. We would like to thank: Kath Dalmeny Adele Jones Christopher Stopes David Gould Stuart Meikle Marie Christine Mehrens Anil Graves Dominic Moran Thomas Harttung Jules Pretty Patrick Holden Hannah Steenbergen for helpful comments on draft versions or sections of the report. All interpretation, opinion and error is the responsibility of the authors alone. Designed by: Alan Carmody, Midas Design Consultants Ltd. and Blue Moon Creative Production Coordinator: Hannah Steenbergen Printed by Vale Press Ltd. First published November 2017 Revised and corrected July 2019 We would like to thank the following organisations for their invaluable support for our work on True Cost Accounting, as well as the Brunswick Group, who kindly hosted our report launch in November 2017: THE HIDDEN COST OF UK FOOD FOREWORD 3 PREFACE TO THE 2019 EDITION 5 PREFACE 7 EXECUTIVE SUMMARY 8 Hidden costs in 2015 ............................................................................................................................................8 Challenges to be overcome .............................................................................................................................10 Addressing the challenges ..............................................................................................................................10 The purpose of this report ...............................................................................................................................10 -

Agrochemicals - the Silent Killers Case Histories
Case histories Agrochemicals - the Silent Killers Rosemary Mason MB, ChB, FRCA and Palle Uhd Jepsen former Conservation Adviser to the Danish Forest and Nature Agency JUSTIFICATION The purpose of this document is to highlight the problems of the current and future use of agrochemical products, using a series of case studies. Have we forgotten Rachel Carson’s Silent Spring from 1962? Many of these chemicals are far more toxic (and persistent) than DDT. They are the silent destroyers of human health and the environment. CONTENTS CASE HISTORIES 2 Honeybees 2 Bumblebees 3 Super-weeds 5 The controversial BBC Countryfile programme 6 Why are the European authorities determined to get GM crops into Europe? 7 EFSA has recently given positive opinions on old herbicides at the request of industry 8 Another GM, herbicide tolerant seed in the pipeline 9 What is the role of the Commissioner of the Health and Consumers Directorate? 9 The effects of GM crops on humans in Latin America 10 Glyphosate-Based Herbicides Produce Teratogenic Effects on Vertebrates by Impairing Retinoic Acid Signaling 13 Danish farmers report side effects with GM Soya fed to pigs 14 Desiccation of crops with glyphosate to dry them 15 Scientists complain that the EC has ignored independent scientific advice about Roundup® 15 RMS (DAR) studies on glyphosate 16 Other EFSA reasoned opinions for modification of MRLs in food 17 Lack of ecological knowledge from industry and governments 17 Humans are bearing the brunt of these genotoxic chemicals and will do so even more 18 The Faroes Statement: Human Health Effects of Developmental Exposure to Chemicals in Our Environment 2007 19 The Permanent Peoples’ Tribunal 19 Peoples’ Submission 19 The Verdict 23 Summary of Verdict by members of the Jury 23 1 Summary of complaints to the Ombudsman 1360/2012/BEH about the EC and EFSA CASE HISTORIES Honeybees Dead queens and workers. -

Insect Biochemistry and Molecular Biology 48 (2014) 51E62
Insect Biochemistry and Molecular Biology 48 (2014) 51e62 Contents lists available at ScienceDirect Insect Biochemistry and Molecular Biology journal homepage: www.elsevier.com/locate/ibmb Identification of pheromone components and their binding affinity to the odorant binding protein CcapOBP83a-2 of the Mediterranean fruit fly, Ceratitis capitata P. Siciliano a,b, X.L. He a, C. Woodcock a, J.A. Pickett a, L.M. Field a, M.A. Birkett a, B. Kalinova c, L.M. Gomulski b, F. Scolari b, G. Gasperi b, A.R. Malacrida b, J.J. Zhou a,* a Department of Biological Chemistry and Crop Protection, Rothamsted Research, Harpenden, Herts. AL5 2JQ, United Kingdom b Dipartimento di Biologia e Biotecnologie, Università di Pavia, Via Ferrata 9, 27100 Pavia, Italia c Institute of Organic Chemistry and Biochemistry of the AS CR, v.v.i., Flemingovo nám. 2, CZ-166 10 Prague 6, Czech Republic article info abstract Article history: The Mediterranean fruit fly (or medfly), Ceratitis capitata (Wiedemann; Diptera: Tephritidae), is a serious Received 30 July 2013 pest of agriculture worldwide, displaying a very wide larval host range with more than 250 different Received in revised form species of fruit and vegetables. Olfaction plays a key role in the invasive potential of this species. Un- 17 February 2014 fortunately, the pheromone communication system of the medfly is complex and still not well estab- Accepted 18 February 2014 lished. In this study, we report the isolation of chemicals emitted by sexually mature individuals during the “calling” period and the electrophysiological responses that these compounds elicit on the antennae Keywords: fl fl of male and female ies. -

Profits and Potatoes
Rothamsted Research and the Value of Excellence: A synthesis of the available evidence Report to Rothamsted Research By Sean Rickard October 2015 Séan Rickard Ltd. 2015 1 Forward by the Director and Chief Executive of Rothamsted Research Professor Achim Dobermann Assessing the impact of agricultural research is difficult because science is a complex and lengthy process, with pathways to impact that vary widely. It is common that research and development stages towards new technologies and know-how last 15 or even more years, followed by many more years for reaching peak adoption by farmers and other users of new technology. Adoption is often slow and diffuse, also because unlike in manufacturing many agricultural innovations need to be tailored to specific biophysical and even socioeconomic environments. Some of the many impact pathways may be known well, whereas others are not or are very difficult to quantify. Attribution presents another problem, i.e., it is often very difficult to quantify how much of the observed technological progress or other impact can be attributed to a specific innovation or an institution. Progress in productivity and efficiency is the result of many factors, including technology, knowledge and policy. Even more difficult is to assess the impact of agricultural technology on a wider range of ecosystem services and consumer benefits. Nevertheless, in science we need to be willing to rigorously assess the relevance of our research. In his report, Sean Rickard has attempted to quantify the cumulative impact Rothamsted Research has had through key impact pathways that are most directly linked to its research. The economic approach used is in my view sound, providing a robust framework and a first overall estimate of the wider impact. -

Rothamsted Repository Download
Patron: Her Majesty The Queen Rothamsted Research Harpenden, Herts, AL5 2JQ Telephone: +44 (0)1582 763133 WeB: http://www.rothamsted.ac.uk/ Rothamsted Repository Download A - Papers appearing in refereed journals Firbank, L. G., Attwood, S., Eory, V., Gadanakis, Y., Lynch, J. M., Sonnino, R. and Takahashi, T. 2018. Grand challenges in sustainable intensification and ecosystem services. Frontiers in Sustainable Food Systems. 2 (7), pp. 1-3. The publisher's version can be accessed at: • https://dx.doi.org/10.3389/fsufs.2018.00007 The output can be accessed at: https://repository.rothamsted.ac.uk/item/84746/grand- challenges-in-sustainable-intensification-and-ecosystem-services. © 28 March 2018, CC-BY license applies 17/09/2019 09:05 repository.rothamsted.ac.uk [email protected] Rothamsted Research is a Company Limited by Guarantee Registered Office: as above. Registered in England No. 2393175. Registered Charity No. 802038. VAT No. 197 4201 51. Founded in 1843 by John Bennet Lawes. SPECIALTY GRAND CHALLENGE published: 28 March 2018 doi: 10.3389/fsufs.2018.00007 Grand Challenges in Sustainable intensification and ecosystem Services Leslie G. Firbank 1*, Simon Attwood 2,3, Vera Eory 4, Yiorgos Gadanakis 5, John Michael Lynch 6, Roberta Sonnino7 and Taro Takahashi8,9 1 School of Biology, University of Leeds, Leeds, United Kingdom, 2 Bioversity International, Maccarese, Italy, 3 School of Environmental Sciences, University of East Anglia, Norwich, United Kingdom, 4 Land Economy, Scotland’s Rural College (SRUC), Edinburgh, United Kingdom, -

HGCA Project Report 504.Pdf
Patron: Her Majesty The Queen Rothamsted Research Harpenden, Herts, AL5 2JQ Telephone: +44 (0)1582 763133 WeB: http://www.rothamsted.ac.uk/ Rothamsted Repository Download D1 - Technical reports: non-confidential Cook, S. M., Doring, T. F., Ferguson, A. W., Martin, J. L., Skellern, M. P., Smart, L. E., Watts, N. P., Welham, S. J., Woodcock, C. M., Pickett, J. A., Bardsley, E., Bowman, J., Burns, S., Clarke, M., Davies, J., Gibbard, C., Johnen, A., Jennaway, R., Meredith, R., Murray, D., Nightingale, M., Padbury, N., Patrick, C., Von Richthofen, J-S., Taylor, P., Tait, M. and Werner, P. 2013. Development of an integrated pest management strategy for control of pollen beetles in winter oilseed rape (HGCA Project Report No 504). Kenilworth Home Grown Cereals Authority (HGCA). The publisher's version can be accessed at: • https://cereals.ahdb.org.uk/media/198124/pr504.pdf The output can be accessed at: https://repository.rothamsted.ac.uk/item/8qvwy/development-of-an-integrated-pest- management-strategy-for-control-of-pollen-beetles-in-winter-oilseed-rape-hgca-project- report-no-504. © 1 February 2013, Home Grown Cereals Authority (HGCA). 29/10/2019 11:38 repository.rothamsted.ac.uk [email protected] Rothamsted Research is a Company Limited by Guarantee Registered Office: as above. Registered in England No. 2393175. Registered Charity No. 802038. VAT No. 197 4201 51. Founded in 1843 by John Bennet Lawes. Feb 2013 Project Report No. 504 Development of an integrated pest management strategy for control of pollen beetles in winter oilseed rape by Samantha M. Cook1, Thomas F. Döring2,3, Andrew W, Ferguson1, Janet L. -

The Development of Horticultural Science in England, 1910-1930
The Development of Horticultural Science in England, 1910-1930 Paul Smith Department of Science and Technology Studies University College London Thesis submitted for the Degree of Doctor of Philosophy July 2016 I, Paul Smith, confirm the work presented in this thesis is my own. Where information has been derived from other sources, I confirm it has been indicated in the thesis. 2 Abstract This thesis explores how horticultural science was shaped in England in the period 1910-1930. Horticultural science research in the early twentieth century exhibited marked diversity and horticulture included bees, chickens, pigeons,pigs, goats, rabbits and hares besides plants. Horticultural science was characterised by various tensions arising from efforts to demarcate it from agriculture and by internecine disputes between government organisations such as the Board of Agriculture, the Board of Education and the Development Commission for control of the innovative state system of horticultural research and education that developed after 1909. Both fundamental and applied science research played an important role in this development. This thesis discusses the promotion of horticultural science in the nineteenth century by private institutions, societies and scientists and after 1890 by the government, in order to provide reference points for comparisons with early twentieth century horticultural science. Efforts made by the new Horticultural Department of the Board of Agriculture and by scientists and commercial growers raised the academic status of -

British Food: What Role Should UK Producers Have in Feeding The
This is a repository copy of British Food- What Role Should UK Food Producers have in Feeding the UK?. White Rose Research Online URL for this paper: https://eprints.whiterose.ac.uk/112876/ Monograph: Doherty, Bob orcid.org/0000-0001-6724-7065, Benton, Tim G., Fastoso, Fernando Javier orcid.org/0000-0002-9760-6855 et al. (1 more author) (2017) British Food- What Role Should UK Food Producers have in Feeding the UK? Research Report. Wm Morrisons plc Reuse Items deposited in White Rose Research Online are protected by copyright, with all rights reserved unless indicated otherwise. They may be downloaded and/or printed for private study, or other acts as permitted by national copyright laws. The publisher or other rights holders may allow further reproduction and re-use of the full text version. This is indicated by the licence information on the White Rose Research Online record for the item. Takedown If you consider content in White Rose Research Online to be in breach of UK law, please notify us by emailing [email protected] including the URL of the record and the reason for the withdrawal request. [email protected] https://eprints.whiterose.ac.uk/ 02/2017 British Food What role should UK producers have in feeding the UK? British Food: What role should UK producers have in feeding the UK? in feeding have UK producers should role What British Food: 02/2017 CONTENTS Chapter 1 03-05 Introduction: Food systems under pressure Chapter 2 06-07 The food we eat: where is it sourced? 02 Chapter 3 08-13 Is more food trade a good idea? -
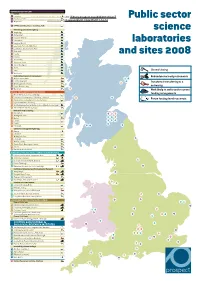
1 Closed/Closing Redundancies/Early Retirements Transferred/Transferring
DEFRA AGENCIES AND LABS CEFAS 1 Lowestoft Latest revision of this document: //library.prospect.org.uk/id/2011/04237 2 Burnham, Essex Public sector 3 Weymouth This revision: //library.prospect.org.uk/id/2011/04237/2011-12-14 4 DEFRA Central Science Laboratory, York Veterinary Laboratories Agency science 5 Weybridge 6 Aberystwyth 7 Bury St Edmunds 8 Carmarthen 9 Langford, Bristol laboratories 10 Lasswade, Penicuik, Midlothian 11 Luddington, Stratford upon Avon 12 Newcastle 13 Penrith and sites 2008 14 Preston 15 Shrewsbury 16 Starcross, Devon 17 Sutton Bonington 18 Thirsk 19 Truro Closed/closing 20 Winchester Horticulture Research International Redundancies/early retirements 21 Wellesbourne, Warks 69 72 22 East Malling, Kent 65 Transferred/transferring to a 23 Efford, Lymington Hants 45 24 Kirton, Boston, Lincs university 25 Wye, Kent 31 Work likely to suffer under current NATURAL ENVIRONMENT RESEARCH COUNCIL 26 British Antarctic Survey, Cambridge funding arrangements 27 Proudman Oceanographic Laboratory, Liverpool 30 70 28 National Oceanography Centre, Southampton Future funding levels uncertain 29 Plymouth Marine Laboratory 30 Scottish Association for Marine Science, Dunstaffnage, Argyll 31 Ardtoe Marine Laboratory, Argyll British Geological Survey 32 Nottingham 10 37 41 33 Wallingford, Oxon 34 Exeter 49 57 64 35 London 67 68 74 36 Cardiff 75 37 Edinburgh 71 73 66 Centre for Ecology and Hydrology 38 Bangor 39 Lancaster 40 Wallingford, Oxon 41 Edinburgh 12 42 Winfrith, Dorset 43 Monks Wood, Huntingdon, Cambs 44 Oxford 13 45 Banchory, Aberdeenshire -

Rothamsted Repository Download
Patron: Her Majesty The Queen Rothamsted Research Harpenden, Herts, AL5 2JQ Telephone: +44 (0)1582 763133 WeB: http://www.rothamsted.ac.uk/ Rothamsted Repository Download A - Papers appearing in refereed journals Rivero, M. J., Lopez-Villalobos, N., Evans, A., Berndt, A., Cartmill, A., Neal, A. L., McLaren, A., Farruggia, A., Mignolet, C., Chadwick, D. R., Styles, D., McCracken, D., Busch, D., Martin, G. B., Fleming, H. R., Sheridan, H., Gibbons, J., Merbold, L., Eisler, M., Lambe, N., Rovira, P., Harris, P., Murphy, P., Vercoe, P. E., Williams, P., Machado, R., Takahashi, T., Puech, T., Boland, T., Ayala, W. and Lee, M. R. F. 2021. Key traits for ruminant livestock across diverse production systems in the context of climate change: perspectives from a global platform of research farms. Reproduction, Fertility and Development. 33 (2), pp. 1- 19. https://doi.org/10.1071/RD20205 The publisher's version can be accessed at: • https://doi.org/10.1071/RD20205 • https://www.publish.csiro.au/rd/RD20205 The output can be accessed at: https://repository.rothamsted.ac.uk/item/981yz/key- traits-for-ruminant-livestock-across-diverse-production-systems-in-the-context-of- climate-change-perspectives-from-a-global-platform-of-research-farms. © 8 January 2021, Please contact [email protected] for copyright queries. 13/01/2021 10:25 repository.rothamsted.ac.uk [email protected] Rothamsted Research is a Company Limited by Guarantee Registered Office: as above. Registered in England No. 2393175. Registered Charity No. 802038. VAT No. 197 4201 51. Founded in 1843 by John Bennet Lawes. CSIRO PUBLISHING Reproduction, Fertility and Development, 2021, 33, 1–19 https://doi.org/10.1071/RD20205 Key traits for ruminant livestock across diverse production systems in the context of climate change: perspectives from a global platform of research farms M.