The Compound Elastic Scattering of 3.15 Mev Neutrons by Calcium-40
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Administrative Atlas , Punjab
CENSUS OF INDIA 2001 PUNJAB ADMINISTRATIVE ATLAS f~.·~'\"'~ " ~ ..... ~ ~ - +, ~... 1/, 0\ \ ~ PE OPLE ORIENTED DIRECTORATE OF CENSUS OPERATIONS, PUNJAB , The maps included in this publication are based upon SUNey of India map with the permission of the SUNeyor General of India. The territorial waters of India extend into the sea to a distance of twelve nautical miles measured from the appropriate base line. The interstate boundaries between Arunachal Pradesh, Assam and Meghalaya shown in this publication are as interpreted from the North-Eastern Areas (Reorganisation) Act, 1971 but have yet to be verified. The state boundaries between Uttaranchal & Uttar Pradesh, Bihar & Jharkhand and Chhattisgarh & Madhya Pradesh have not been verified by government concerned. © Government of India, Copyright 2006. Data Product Number 03-010-2001 - Cen-Atlas (ii) FOREWORD "Few people realize, much less appreciate, that apart from Survey of India and Geological Survey, the Census of India has been perhaps the largest single producer of maps of the Indian sub-continent" - this is an observation made by Dr. Ashok Mitra, an illustrious Census Commissioner of India in 1961. The statement sums up the contribution of Census Organisation which has been working in the field of mapping in the country. The Census Commissionarate of India has been working in the field of cartography and mapping since 1872. A major shift was witnessed during Census 1961 when the office had got a permanent footing. For the first time, the census maps were published in the form of 'Census Atlases' in the decade 1961-71. Alongwith the national volume, atlases of states and union territories were also published. -

List of Sewa Kendras Retained
List 2 - List of Sewa Kendras Retained List 2 - List of Sewa Kendras Retained S No District Sewa Kendra Name and Location Center Code Type 1 Amritsar Suwidha Centre, HO, Kitchlu Chownk PB-049-00255-U025 Type-I 2 Amritsar MC Majitha Near Telephone Exchange PB-049-00255-U001 Type-II 3 Amritsar MC Jandiala Near Bus Stand PB-049-00255-U002 Type-II 4 Amritsar Chamrang Road (Park) PB-049-00255-U004 Type-II 5 Amritsar Gurnam Nagar/Sakatri Bagh PB-049-00255-U008 Type-II 6 Amritsar Lahori Gate PB-049-00255-U011 Type-II 7 Amritsar Kot Moti Ram PB-049-00255-U015 Type-II 8 Amritsar Zone No 6 - Basant Park, Basant Avenue PB-049-00255-U017 Type-II Zone No 7 - PWD (B&R) Office Opp. 9 Amritsar PB-049-00255-U019 Type-II Celebration Mall 10 Amritsar Zone No 8- Japani Mill (Park), Chherata PB-049-00255-U023 Type-II Suwidha Centre, DTO Office, Ram Tirath 11 Amritsar PB-049-00255-U026 Type-II Road, Asr 12 Amritsar Suwidha Centre, Ajnala PB-049-00255-U028 Type-II Suwidha Centre, Batala Road, Baba 13 Amritsar PB-049-00255-U029 Type-II Bakala Sahib 14 Amritsar Suwidha Centre, Attari PB-049-00255-U031 Type-II 15 Amritsar Suwidha Centre, Lopoke PB-049-00255-U032 Type-II 16 Amritsar Suwidha Centre, Tarsikka PB-049-00255-U034 Type-II 17 Amritsar Ajnala PB-049-00255-R001 Type-II 18 Amritsar Ramdass PB-049-00255-R002 Type-III 19 Amritsar Rajasansi PB-049-00259-R003 Type-II 20 Amritsar Market Committee Rayya Office PB-049-00259-R005 Type-II 21 Amritsar Jhander PB-049-00255-R025 Type-III 22 Amritsar Chogawan PB-049-00255-R027 Type-III 23 Amritsar Jasrur PB-049-00255-R035 -

Kapurthala District, Punjab
क� द्र�यू�म भ जल बोड셍 जल संसाधन, नद� �वकास और गंगा संर�ण मंत्रालय भारत सरकार Central Ground Water Board Department of Water Resources, River Development and Ganga Rejuvenation Government of India Report on AQUIFER MAPPING AND MANAGEMENT PLAN Kapurthala District, Punjab उ�र� पि�चम �ेत्र, चंडीगढ़ North Western Region, Chandigarh Aquifer Mappingg and Management Plan of Kapurthala District, PunjabPunja State 1.0 INTRODUCTION The primary objectivetive of the Aquifer Mapping can be summedmed up as “Know your Aquifer, Manage your Aquiferifer”. Demystification of Science and therebyby involvement of stake holders is the essence off ththe entire project. The involvement andnd participation of the community will infuse a sensense of ownership amongst the stakeholders. ThiThis is an activity where the Government and the Commommunity work in tandem. Greater the harmormony between the two, greater will be the chancess of successful implementation and achievemenment of the goals of the Project. As per the Report of tthe Working Group on Sustainable Groundnd Water Management, “It is imperative to designn aan aquifer mapping programme with a clearcle -cut groundwater management purpose. Thisis wwill ensure that aquifer mapping does not remain an academic exercise and that it will seaseamlessly flow into a participatory groundundwater management programme. The aquifer mappapping approach can help integrate groundd wwater availability with ground water accessibility and quality aspects. 1.2 Scope of the study: Systematic mappingg of an aquifer encompasses a host of activitiesies suchs as collection and compilation of available informformation on aquifer systems, demarcation of ththeir extents and their characterization, analysis of ddata gaps, generation of additional data for filling the identified data gaps and finally, preparatiaration of aquifer maps at the desired scale. -

Village & Townwise Primary Census Abstract, Kapurthala, Part X-A & B, Series-17, Punjab
CENSUS 1971 PARTS X-A & B VILLAGE & TOWN SERIES 17 DIRECTORY PUNJAB VILLAGE & TOWNWISE PRIMARY CENSUS ABSTRACT DISTRICT CENSUS KAPURTHALA HANDBOOK DISTRICT P. L. SONDHI H. S. KWATRA OF THE INDIAN ADMINISTRATIVE SERVICE OF THE PUNJAB CIVil, SERVICE Ex-Officio Director of Census Opemtions Deputy Director of Census Opemtions PUNJAB PUNJAB Motif-- GURDWARA BER SAHIB, SULTANPUR LODHI Gurdwara Be?" Sahib is a renowned place of pilgrimage of the Sikhs. It is situated at Sultanpur Lodhi, 16 miles South of Kapurthala, around a constellation of other Gurdwaras (Sikh Temples) associated with the early life of Guru Nanak Dev. It is n:a,.med after the 'Ber', tree under which Guru Nanak Dev used to meditate. Legend has it that sterile women beget child7'en after takinq leaves of this tree. The old Gu'rdwara was re-constructed by the joint effo'rts of Maharaja Jagatjit Singh of Kapurthala, Maharaja Yadvindra Singh of Patiala and Bhai Arjan Singh of Bagrian. A big fair is held at this Gurdwara on Guru Nanak Dev's birthday. Motif by : J. S. Gill. 15 '40' PUNJAB DISTRICT KAPURTHALA s· KILOIUTRES S o 5 10 15 20 4 8 12 MILES 4 o· 3 " Q TO JUL LlJNDllR <' ~O "'''<, U ""a". I. \.. u .) . 31 DISTRICT 80UNOARV..... POST' TtLEGftAPH OFfiCE "................. P'T TAHSIL BOUNDARY.. _TALlil PRIMARV HEALTH DISTRICT HEADQUARTERS .. CENTRE S IMATERNITY • CHIlD T"HSIL HEADQUARTERS. WELfARE CENTRES ............... - ... $ NATIONAL HIGHWAY .. liECONDARY SCHOOL./COl.LEGE .............•..• , OTHER METAI.LED ROAII.. 45 BROAD GAUGE RAILWAYS WITH STATIOfll. ... RS 4 RIVER .. - CANAL .. UklAII AREA •.. RUT HOUSE .... VILLAQES HAVING POPULATION 5000+ URBAN POPULATION " 50.000 PERSONS 10.000 •.. -

241, Industrial Area, Near Quark City, Phase – 8B, Sector – 74 Mohali – 160071
Government of Punjab Punjab State e-Governance Society O/o Directorate of Governance Reforms Plot No. D- 241, Industrial Area, Near Quark City, Phase – 8B, Sector – 74 Mohali – 160071 Corrigendum – 1 EoI Reference No: PSeGS/PAWAN/2018/01 Eol for high speed last mile connectivity solution FOR VERTICAL/ HORIZONTAL EXPANSION OF PAWAN NETWORK to connect government offices, service delivery centers and other important sites in the State. It is hereby intimated that some discrepancies were observed in the latitude & longitude information at Annexure – 1 of the above mentioned EoI. The rectification has been made and the amended Annexure is provided at Page 2. The summary of discrepancies and rectification as under:- Sl. No. Discrepancy Rectification (refer amended Annexure) 1 There is Latitude / Longitude 11 locations corrected and highlighted in discrepancy at 11 Locations green colour 2 Duplicate Latitude / Longitude 24 locations corrected and highlighted in found at 26 locations green colour 2 duplicate locations highlighted in red colour to be deleted. 3 Sites in Sangrur not provided yet Information regading sites of Sangrur District has been added 4 Locations of District PoPs not District PoP (DC Office) are highlighted in provided yellow colour Member Secretary Annexure S.NO District Headquarters Count 1 Amritsar 162 2 Barnala 61 3 Bathinda 128 4 Faridkot 84 5 Fatehgarh Sahib 74 6 Fazilka 85 7 Firozpur 89 8 Gurdaspur 170 9 Hoshiarpur 132 10 Jalandhar 158 11 Kapurthala 93 12 Ludhiana 263 13 Mansa 76 14 Moga 82 15 Mohali 74 16 Muktsar Sahib -

S. No. District Zone Sewa Kendra Name and Location MDDS Village
S. No. District Zone Sewa Kendra Name and Location MDDS Village Code Type 1 Amritsar Zone I Suwidha Centre, HO, Kitchlu Chownk PB-049-00255-U025 Type-I 2 Amritsar Zone I MC Majitha Near Telephone Exchange PB-049-00255-U001 Type-II 3 Amritsar Zone I MC Jandiala Near Bus Stand PB-049-00255-U002 Type-II 4 Amritsar Zone I Chamrang Road (Park) PB-049-00255-U004 Type-II 5 Amritsar Zone I Gurnam Nagar/Sakatri Bagh PB-049-00255-U008 Type-II 6 Amritsar Zone I Lahori Gate PB-049-00255-U011 Type-II 7 Amritsar Zone I Kot Moti Ram PB-049-00255-U015 Type-II 8 Amritsar Zone I Zone No 6 - Basant Park, Basant Avenue PB-049-00255-U017 Type-II 9 Amritsar Zone I Zone No 7 - PWD (B&R) Office Opp. Celebration Mall PB-049-00255-U019 Type-II 10 Amritsar Zone I Zone No 8- Japani Mill (Park), Chherata PB-049-00255-U023 Type-II 11 Amritsar Zone I Suwidha Centre, DTO Office, Ram Tirath Road, Asr PB-049-00255-U026 Type-II 12 Amritsar Zone I Suwidha Centre, Ajnala PB-049-00255-U028 Type-II 13 Amritsar Zone I Suwidha Centre, Batala Road, Baba Bakala Sahib PB-049-00255-U029 Type-II 14 Amritsar Zone I Suwidha Centre, Attari PB-049-00255-U031 Type-II 15 Amritsar Zone I Suwidha Centre, Lopoke PB-049-00255-U032 Type-II 16 Amritsar Zone I Suwidha Centre, Tarsikka PB-049-00255-U034 Type-II 17 Amritsar Zone I Ajnala PB-049-00255-R001 Type-II 18 Amritsar Zone I Ramdass PB-049-00255-R002 Type-II 19 Amritsar Zone I Rajasansi PB-049-00259-R003 Type-II 20 Amritsar Zone I Market Committee Rayya Office PB-049-00259-R005 Type-II 21 Amritsar Zone I Jhander PB-049-00255-R025 Type-III -

Sultanpur Lodhi Assembly Punjab Factbook | Key Electoral Data of Sultanpur Lodhi Assembly Constituency | Sample Book
Editor & Director Dr. R.K. Thukral Research Editor Dr. Shafeeq Rahman Compiled, Researched and Published by Datanet India Pvt. Ltd. D-100, 1st Floor, Okhla Industrial Area, Phase-I, New Delhi- 110020. Ph.: 91-11- 43580781-84 Email : [email protected] Website : www.indiastatelections.com Online Book Store : www.indiastatpublications.com Report No. : AFB/PB-028-0121 ISBN : 978-93-5301-582-4 First Edition : January, 2018 Third Updated Edition : January, 2021 Price : Rs. 11500/- US$ 310 © Datanet India Pvt. Ltd. All rights reserved. No part of this book may be reproduced, stored in a retrieval system or transmitted in any form or by any means, mechanical photocopying, photographing, scanning, recording or otherwise without the prior written permission of the publisher. Please refer to Disclaimer at page no. 170 for the use of this publication. Printed in India Contents No. Particulars Page No. Introduction 1 Assembly Constituency - (Vidhan Sabha) at a Glance | Features of Assembly 1-2 as per Delimitation Commission of India (2008) Location and Political Maps Location Map | Boundaries of Assembly Constituency - (Vidhan Sabha) in 2 District | Boundaries of Assembly Constituency under Parliamentary 3-10 Constituency - (Lok Sabha) | Town & Village-wise Winner Parties- 2019, 2017, 2014, 2012 and 2009 Administrative Setup 3 District | Sub-district | Towns | Villages | Inhabited Villages | Uninhabited 11-23 Villages | Village Panchayat | Intermediate Panchayat Demographic 4 Population Households | Rural/Urban Population | Towns and -

Village & Townwise Primary Census Abstract, Kapurthala, Part XII-A & B
CENSUS OF INDIA 1991 SERIES-20 PUNJAB DISTRICT CENSUS HAND·BOOK PA'RT XII-A & lB VILLAGE & T.OWN DrRECTORY VILLAGE & TOWNWISE .PRIMAR Y CENSUS ABSTRACT DISTRICT KAPURTHALA DIrector of Census Operations Punjab Published by : The Government of Punjab, 1996 PUNJAB DISTRICT KAPURTHALA ~m5 o 5 10 I5 20 Km q.. ~ \. '" q.. ,.. + A.., (J \. q. '" "" () " A.., .. l ;:;p. (" ~• ; ~ \ "z 0 s '{ .. BOUNDARY, DISTRICT _.-..- C.O. BLOCKS TAHSIL A NAOALA " C.D. BLOCK .' .. ........ .. , .. ...... " .. 1"" "e B I(APURTHALA H€ADOUARTERS: DlSTRlCTj TAHSIL .. ... .. .. @; @ C SUL TANPUR LOOM' NATIONAL HIGHWAY .......... .... .•. •. .. _...;,;N""'H.;..'_ o PHAGWARA IMPORTANT METALLED ROAD .. ........ .. " .... e' _-=__ RA!lWAY LINE WITH STATION, BROAD GAUGE: eo •• ' _~ RIVER AND STREAM .. .. .. .. .' .. .. ~ VILLAGE HAVING 5000 AND A90JE POPULATION WITH NAME ... ...... .. ...... .. .. .. .. .. .... Oh«wan• All Ixlondaries 0,. up«lted ullo I~ D«:embor, 1989. URBAN AREA WITH POP\JLATION SIZE CLASS II S IV •• POST AND TELEGRAPH OFFICE .. .. .. .. .. .. .. .. .. PTO DEGREE COLl.EG£ AND TECt-tlICAL INSTITUTION.. .. I!!!l m REST HOUSE RH DISTRICT H£ADQUARTERS IS AlSO TAHSL HEADQUARTERS 80sed upon Survey 01 IIIdkl map .llh the permission 01 the Sur~eyor 0._11 .f 1MiI. © GovlI'nmIIII of In4Ia Cop,,~t. 897. CENSUS OF INDlA-199i A-CENTRAL GOVERNMENT PUBLICATIONS ··Tho publications relating to Punjab bear Series No. 20 and will bo published as follows :- part I·A Administration Report- Enumeration (for official use only). Pa.rt l-B Admi nistration Report-Ta bulatio n (for official use only), "- Part II·A General Population Tables 1 and and r Combined Volume. Pan lI·B Primary Census Abstract J Part III General Economic Tables. -
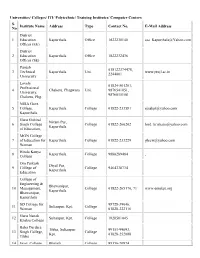
List of Educational Institutes in Kapurthala
Universities/ Colleges/ ITI/ Polytechnic/ Training Institutes/ Computer Centers S. Institute Name Address Type Contact No. E-Mail Address No District 1 Education Kapurthala Office 1822230140 [email protected] Officer (EE) District 2 Education Kapurthala Office 1822232436 Officer (SE) Punjab 018122374478, 3 Technical Kapurthala Uni. www.ptujl.ac.in 2244001 University Lovely 01824-501201, Professional 4 Chaheru, Phagwara Uni. 9876541051, University, 9876015108 Chaheru, Phg. NJSA Govt. 5 College, Kapurthala College 01822-233581 [email protected] Kapurthala Guru Gobind Nizam Pur, 6 Singh College College 01822-260202 [email protected] Kapurthala of Education, MGN College 7 of Education for Kapurthala College 01822-233229 [email protected] Woman Hindu Kanya 8 Kapurthala College 9888289484 College Om Parkash Diyal Pur, 9 College of College 9464338734 Kapurthala Education College of Engineering & Bhawanipur, 10 Management, College 01822-265170, 71 www.eemkpt.org Kapurthala Bhawanipur, Kapurthala SD College for 98728-39046, 11 Sultanpur, Kpt. College Woman 01828-222116 Guru Nanak 12 Sultanpur, Kpt. College 1828501045 Khalsa College Baba Dardara Tibba, Sultanpur, 99151-99693, 13 Singh College, College Kpt. 01828-252888 Tibba 14 Govt. College, Bhulath College 98156-70874 Bhulath GNPKM 15 Nadala, Bhulath College 01822-272827 College, Nadala SPS Khalsa College, 16 Begowal, Bhulath College 98154-31389 Begowal, Bhulath Shri Guru Harkrishan Harkrishan Nagar, 17 Institute of Gali No. 3, Banga College 01824-271324 Technoligy Road, Phg. & Management GN Institute Health & 18 Atholi College 98729-77182 Research, Atholi Shri Guru Ravi Hoshiarpur Chowk, 19 Dass ITI College 01824-228695 Phg. College, Phg Kamla Nehru Hoshiarpur Chowk, 20 College for College 01824-228137 Phg. Woman Guru Nanak Ramgarhia Bhai 21 Phagwara College 01824-501920 Lalo College, Phg Baba Himat 22 Singh Technical GT Road, Phg. -

Public Notice No STC-P(P-1)/ 22M6o Dated: -12021
Public Notice No STC-P(P-1)/ 22M6o Dated: -12021 With a view to provide more/dircct bus scrvice to the traveling public on the following routes falling on the Highways/Roads within the State of Punjab, based on the need got asscssed from the offices of respective Secretary RTAs, applications are hereby invited from the intcnding applicants/gcncral public who are natives of Punjab State, for the grant of rogular stage carriage permits with return trips as mentioned against cach route for big buses (having seating capacity of 39 or more) as per the provisions of the Punjab Transport Scheme 2018 dated 22.02.2018 as modified on 04.06.2019. As per the approved Transport Scheme, the stage carriage permits on the routes falling on National Highways and State Highways/Major District Roads/0ther Roads shall be granted in favour of the STUs and the Private Operators in the ratio of 50:50 and 40:60 respectively. Separate application shall be made for each route: Sr. Name of route Major No. of No of No. portion Permit return of the trip route falls on Ludhiana-Amritsar via Jalandhar, Kapurthala,| NH Goindwal, Tarn Taran 2 Amritsar-Khem Karan via Chabal Kalan, Bhikhiwind NH Amritsar-Jalandhar via Tarn Taran, Goindwal NH 2 3 Sahib, Kapurthala Ludhiana-Dera Baba Nanak via Phillaur, Phagwara, | NH Jalandhar, Beas, Batala Amritsar-Barnala via Tarn Taran, Harike, Makhu, NH Moga Tarn Taran-Harchowal via Amritsar NH 3 7 Amritsar-Naushera via Chheharta, Khassa, NH Gharinda, Ranike Mour, Attari, Naushera Dalla Amritsar-Talwara via Mehta, Sri Hargobindpur, -

Kapurthala District, No-15 , Punjab
CENSUS OF INDIA 1961 PUNJAB DISTRICT CENSUS HANDBOOK No. 15 KAPUR THALA DISTRICT R. L.ANAND Superintendent of Census Operations, Punjab, HarYana, and Union Territory of Chandigarh Published by the Oovernmen~ of Punjab 1967 Price Rs. 18.75 ' ." o ... ..... .. ... PI •H • r.... ~~., .. " " 1('''''''' ••••••( ... " ., " , "" ! '~'\, • / :".: ".._., ,. \' ........ _.,.-.~., 1. .... ( ,.. ~"~:..,.... ~'. : \ .... j ,.". ..... ) '"' . ,J "'" I " '"tt •,. ') ~ > > III III ') II: I- bI ..... III 2 0 '"oJ oJ 2 lII: I I I jj 0 .. @O z • a 0 ;) I- 1/1 Q. 1/1 U a: III )- II: :::I 11.1 ~ 0 0 e t- >:- II: l-'" 0 a iJ f- a: II: e .J 1/1 e II: e 1&1 0 e z :::I :::I II. IIJ z II: 0 0 a a III :::I e U 0 0 a: U 0 e I- UI 0 II: e Z m '"~ II: III Z 0 :::I 1:'" X IIJ '"0 I- e 0 '"U Z I- U It .J'" :::I U .J "IIJ 0 .J a: .J Z e 0 a: e I&. l- e III e 1/1 " l- e I- m LLI III 0 > z III :z: 0 e e a: " ~(.: Y~ a: 'II: U' Q I- :::I CENSUS OF INDIA 1961 A-CENTRAL GOVERNMENT PUBLICA nONS The publications relating to Punjaj bear Volume No. XIII, and are bound separately as follows:- General Report Part IV-A RePort on Housing and Establish ments Report on Vital Statistics Part IV-B Tables on Housing and Establish ments Part I-CO) Subsidiary Tables Part V-A Special Tables on Scheduled Castes and Scheduled Trib,.., Part I -CUi) Subsidiary Ta bles Part V-B Ethnographic Notes on Scheduled Castes and Scheduled Tribes Part II-A General Population Ta bles Part VI Village Survey Monographs : 44 in number, each relating to an individual village Part II-B (i) General Economic Tables (Tables Part VII-A Report on Selected Handicrafts B-I to B-IV. -

EXPRESSION of INTEREST Department of Governance Reforms
EXPRESSION OF INTEREST Department of Governance Reforms - Punjab EoI reference number: PSeGS/PAWAN/2018/01 EoI for high speed last mile connectivity solution FOR VERTICAL/ HORIZONTAL EXPANSION OF PAWAN NETWORK to connect government offices, service delivery centers and other important sites in the State. D - 241, PHASE 8B, INDUS TRIAL AREA,SECTOR 74 , MOHALI, PUNJAB INTRODUCTION The Government of Punjab has established Punjab State Wide Area Network (PAWAN) which has 193 Points of Presence (PoPs). PAWAN is integrated with NICNET using 1Gbps high speed wired connectivity up to all the 22-district headquarters. From district headquarters to Sub Divisional Offices, connectivity of 2/4 Mbps wired connectivity is available. However, the State is planning to migrate this to the proposed solution. The State is interested in going for a cost effective high speed, secured and dedicated connectivity solution for all kinds of its data / audio / video / collaborative applications. The solution would use existing connectivity of 1Gbps which is available at district headquarters and take it to around 2500 identified urban / semi-urban / rural locations of various departments across the state in the first phase. Since the State would be using its own connectivity, there will be no requirement of the paid bandwidth. As part of the solution, the solution provider would guarantee a minimum bandwidth of 50 Mbps through its proposed solution (media) at all of these locations. Punjab State e Governance Society (PSeGS), Department of Governance Reforms (DGR) invites Expression of Interest (EoI) from IT/ Telecom Solution Providers for enabling the last mile connectivity to identified urban / semi-urban / rural locations as per the detailed features as contained in this document.