Modeling a Performance in Indian Classical Music: Multinomial
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

January, 2017 Raga Koushikranjani (Kaishikranjani,Chandrahas,Bahaderkouns, Chandramukhitypeii) in This Month We Shall Study Raga Koushikranjani
Raga of the Month- January, 2017 Raga Koushikranjani (Kaishikranjani,Chandrahas,BahaderKouns, ChandramukhiTypeII) In this month we shall study Raga Koushikranjani. This raga was introduced by Late Pandit Chidanand Nagarkar*. The Raga is based on the platform of Raga Chandrakouns. Shuddha Rishabh is introduced in Arohi as well as Avarohi order and Pancham is varjya swara. The Scale of the Raga Koushikranjani is SRgMdN. The Raga is included in Asavari Thata and in Melakartha No. 21 Kirwani in Carnatic Music. Raga Nadasanjivi of Carnatic Music resembles Raga Koushikranjini closely. Although Chandrakouns effect is prominent in this raga, phrases SRg-Rs and SRgM (without stress or elongation of Komal Gandhar) hints Raga Abhogi. Phrase SRM, which is a characteristic phrase of Raga Chandraprabha, is avoided. Aroha: SRgMdNS’’; Avaroha: S’’ NdMgRS; Vadi - Madhyama; Samvadi- Shadja; Chalan- S, ‘N’d, ‘N, S; ‘g’M’d’NS; ‘NSR ‘NS‘d, ‘N-S; SRgRS, SRgM, gRgM, gMd, MgR, RgMS, ‘d’NS; gMdN, N, MdMN, dNS’’, NS’’ d-M, gRgM, gRS; SRgM, gMd, MdN, dNS’’, S’’R’’g’’M’’R’’S’’, NS’’R’’ NS’’ d, MgMd, MgR- gMRS. The Raga is documented in the book Abhinav Raga Darpan by Pandit K B Kunte and (as Raga Chandrahas) in Volume II of Raga-Darshana by Pandit Manikbua Thakurdas. (Raga Nadasanjivi- Ref. RagaPravaham-by Dr. M N Dhandapani and D Pattamal) * CHIDANAND DATTATREY NAGARKAR, was born in 1919 in Bangalore. Chidanand inherited all his musical talents from his father, who had a flair for singing Bhajans and stage acting (including Natya Sangeet). Chidanand received rigorous training under Acharya Pandit S.N.Ratanjankar and Ustad Agha Samshuddin Hyder for six years. -

1 Syllabus for MA (Previous) Hindustani Music Vocal/Instrumental
Syllabus for M.A. (Previous) Hindustani Music Vocal/Instrumental (Sitar, Sarod, Guitar, Violin, Santoor) SEMESTER-I Core Course – 1 Theory Credit - 4 Theory : 70 Internal Assessment : 30 Maximum Marks : 100 Historical and Theoretical Study of Ragas 70 Marks A. Historical Study of the following Ragas from the period of Sangeet Ratnakar onwards to modern times i) Gaul/Gaud iv) Kanhada ii) Bhairav v) Malhar iii) Bilawal vi) Todi B. Development of Raga Classification system in Ancient, Medieval and Modern times. C. Study of the following Ragangas in the modern context:- Sarang, Malhar, Kanhada, Bhairav, Bilawal, Kalyan, Todi. D. Detailed and comparative study of the Ragas prescribed in Appendix – I Internal Assessment 30 marks Core Course – 2 Theory Credit - 4 Theory : 70 Internal Assessment : 30 Maximum Marks : 100 Music of the Asian Continent 70 Marks A. Study of the Music of the following - China, Arabia, Persia, South East Asia, with special reference to: i) Origin, development and historical background of Music ii) Musical scales iii) Important Musical Instruments B. A comparative study of the music systems mentioned above with Indian Music. Internal Assessment 30 marks Core Course – 3 Practical Credit - 8 Practical : 70 Internal Assessment : 30 Maximum Marks : 100 Stage Performance 70 marks Performance of half an hour’s duration before an audience in Ragas selected from the list of Ragas prescribed in Appendix – I Candidate may plan his/her performance in the following manner:- Classical Vocal Music i) Khyal - Bada & chota Khyal with elaborations for Vocal Music. Tarana is optional. Classical Instrumental Music ii) Alap, Jor, Jhala, Masitkhani and Razakhani Gat with eleaborations Semi Classical Music iii) A short piece of classical music /Thumri / Bhajan/ Dhun /a gat in a tala other than teentaal may also be presented. -
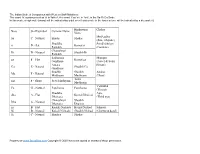
Note Staff Symbol Carnatic Name Hindustani Name Chakra Sa C
The Indian Scale & Comparison with Western Staff Notations: The vowel 'a' is pronounced as 'a' in 'father', the vowel 'i' as 'ee' in 'feet', in the Sa-Ri-Ga Scale In this scale, a high note (swara) will be indicated by a dot over it and a note in the lower octave will be indicated by a dot under it. Hindustani Chakra Note Staff Symbol Carnatic Name Name MulAadhar Sa C - Natural Shadaj Shadaj (Base of spine) Shuddha Swadhishthan ri D - flat Komal ri Rishabh (Genitals) Chatushruti Ri D - Natural Shudhh Ri Rishabh Sadharana Manipur ga E - Flat Komal ga Gandhara (Navel & Solar Antara Plexus) Ga E - Natural Shudhh Ga Gandhara Shudhh Shudhh Anahat Ma F - Natural Madhyam Madhyam (Heart) Tivra ma F - Sharp Prati Madhyam Madhyam Vishudhh Pa G - Natural Panchama Panchama (Throat) Shuddha Ajna dha A - Flat Komal Dhaivat Dhaivata (Third eye) Chatushruti Shudhh Dha A - Natural Dhaivata Dhaivat ni B - Flat Kaisiki Nishada Komal Nishad Sahsaar Ni B - Natural Kakali Nishada Shudhh Nishad (Crown of head) Så C - Natural Shadaja Shadaj Property of www.SarodSitar.com Copyright © 2010 Not to be copied or shared without permission. Short description of Few Popular Raags :: Sanskrut (Sanskrit) pronunciation is Raag and NOT Raga (Alphabetical) Aroha Timing Name of Raag (Karnataki Details Avroha Resemblance) Mood Vadi, Samvadi (Main Swaras) It is a old raag obtained by the combination of two raags, Ahiri Sa ri Ga Ma Pa Ga Ma Dha ni Så Ahir Bhairav Morning & Bhairav. It belongs to the Bhairav Thaat. Its first part (poorvang) has the Bhairav ang and the second part has kafi or Så ni Dha Pa Ma Ga ri Sa (Chakravaka) serious, devotional harpriya ang. -

Syllabus for Post Graduate Programme in Music
1 Appendix to U.O.No.Acad/C1/13058/2020, dated 10.12.2020 KANNUR UNIVERSITY SYLLABUS FOR POST GRADUATE PROGRAMME IN MUSIC UNDER CHOICE BASED CREDIT SEMESTER SYSTEM FROM 2020 ADMISSION NAME OF THE DEPARTMENT: DEPARTMENT OF MUSIC NAME OF THE PROGRAMME: MA MUSIC DEPARTMENT OF MUSIC KANNUR UNIVERSITY SWAMI ANANDA THEERTHA CAMPUS EDAT PO, PAYYANUR PIN: 670327 2 SYLLABUS FOR POST GRADUATE PROGRAMME IN MUSIC UNDER CHOICE BASED CREDIT SEMESTER SYSTEM FROM 2020 ADMISSION NAME OF THE DEPARTMENT: DEPARTMENT OF MUSIC NAME OF THE PROGRAMME: M A (MUSIC) ABOUT THE DEPARTMENT. The Department of Music, Kannur University was established in 2002. Department offers MA Music programme and PhD. So far 17 batches of students have passed out from this Department. This Department is the only institution offering PG programme in Music in Malabar area of Kerala. The Department is functioning at Swami Ananda Theertha Campus, Kannur University, Edat, Payyanur. The Department has a well-equipped library with more than 1800 books and subscription to over 10 Journals on Music. We have gooddigital collection of recordings of well-known musicians. The Department also possesses variety of musical instruments such as Tambura, Veena, Violin, Mridangam, Key board, Harmonium etc. The Department is active in the research of various facets of music. So far 7 scholars have been awarded Ph D and two Ph D thesis are under evaluation. Department of Music conducts Seminars, Lecture programmes and Music concerts. Department of Music has conducted seminars and workshops in collaboration with Indira Gandhi National Centre for the Arts-New Delhi, All India Radio, Zonal Cultural Centre under the Ministry of Culture, Government of India, and Folklore Academy, Kannur. -

Fusion Without Confusion Raga Basics Indian
Fusion Without Confusion Raga Basics Indian Rhythm Basics Solkattu, also known as konnakol is the art of performing percussion syllables vocally. It comes from the Carnatic music tradition of South India and is mostly used in conjunction with instrumental music and dance instruction, although it has been widely adopted throughout the world as a modern composition and performance tool. Similarly, the music of North India has its own system of rhythm vocalization that is based on Bols, which are the vocalization of specific sounds that correspond to specific sounds that are made on the drums of North India, most notably the Tabla drums. Like in the south, the bols are used in musical training, as well as composition and performance. In addition, solkattu sounds are often referred to as bols, and the practice of reciting bols in the north is sometimes referred to as solkattu, so the distinction between the two practices is blurred a bit. The exercises and compositions we will discuss contain bols that are found in both North and South India, however they come from the tradition of the North Indian tabla drums. Furthermore, the theoretical aspect of the compositions is distinctly from the Hindustani, (north Indian) tradition. Hence, for the purpose of this presentation, the use of the term Solkattu refers to the broader, more general practice of Indian rhythmic language. South Indian Percussion Mridangam Dolak Kanjira Gattam North Indian Percussion Tabla Baya (a.k.a. Tabla) Pakhawaj Indian Rhythm Terms Tal (also tala, taal, or taala) – The Indian system of rhythm. Tal literally means "clap". -

Hindustani Classic Music
HINDUSTANI CLASSIC MUSIC: Junior Grade or Prathamik : Syllabus : No theory exam in this grade Swarajnana Talajnana essential Ragajnana Practicals: 1. Beginning of swarabyasa - in three layas 2. 2 Swaramalikas 5 Lakshnageete Chotakyal Alap - 4 ragas Than - 4 Drupad - should be practiced 3. Bhajan - Vachana - Dasapadas 4. Theental, Dadara, Ektal (Dhruth), Chontal, Juptal, Kheruva Talu - Sam-Pet-Husi-Matras - should practice Tekav. 5. Swarajnana 6. Knowledge of the words - nada, shruthi, Aroha, Avaroha, Vadi - Samvedi, Komal - Theevra - Shuddha - Sasthak - Ganasamay - Thaat - Varjya. 7. Swaralipi - should be learnt. Senior Grade: (Madhyamik) Syllabus : Theory: 1. Paribhashika words 2. Sound & place of emergence of sound 3. The practice of different ragas out of “thaat” - based on Pandith Venkatamukhi Mela System 4. To practice ragalaskhanas of different ragas 5. Different Talas - 9 (Trital, Dadra, Jup, Kherva, Chantal, Tilawad, Roopak, Damar, Deepchandi) explanation of talas with Tekas. 6. Chotakhyal, Badakhyal, Bhajan, Tumari, Geethprakaras - Lakshanas. 7. Life history of Jayadev, Sarangdev, Surdas, Purandaradas, Tansen, Akkamahadevi, Sadarang, Kabeer, Meera, Haridas. 8. Knowledge of musical instrument Practicals: 1. Among 20 ragas - Chotakhyal in each 2. Badakhyal - for 10 ragas (Bhoopali, Yamani, Bheempalas, Bageshree, Malkonnse, Alhaiah Bilawal, Bahar, Kedar, Poorvi, Shankara. 3. Learn to sing one drupad in Tay, Dugun & Changun - one Damargeete. VIDHWAN PROFICIENCY Syllabus: Theory 1. Paribhashika Shabdas. 2. 7 types of Talas - their parts (angas) 3. Tabala bol - Tala Jnana, Vilambitha Ektal, Jumra, Adachontal, Savari, Panjabi, Tappa. 4. Raga lakshanas of Bhairav, Shuddha Sarang, Peelu, Multhani, Sindura, Adanna, Jogiya, Hamsadhwani, Gandamalhara, Ragashree, Darbari, Kannada, Basanthi, Ahirbhairav, Todi etc., Alap, Swaravisthara, Sama Prakruthi, Ragas criticism, Gana samay - should be known. -

Rakti in Raga and Laya
VEDAVALLI SPEAKS Sangita Kalanidhi R. Vedavalli is not only one of the most accomplished of our vocalists, she is also among the foremost thinkers of Carnatic music today with a mind as insightful and uncluttered as her music. Sruti is delighted to share her thoughts on a variety of topics with its readers. Rakti in raga and laya Rakti in raga and laya’ is a swara-oriented as against gamaka- complex theme which covers a oriented raga-s. There is a section variety of aspects. Attempts have of exponents which fears that ‘been made to interpret rakti in the tradition of gamaka-oriented different ways. The origin of the singing is giving way to swara- word ‘rakti’ is hard to trace, but the oriented renditions. term is used commonly to denote a manner of singing that is of a Yo asau Dhwaniviseshastu highly appreciated quality. It swaravamavibhooshitaha carries with it a sense of intense ranjako janachittaanaam involvement or engagement. Rakti Sankarabharanam or Bhairavi? rasa raga udaahritaha is derived from the root word Tyagaraja did not compose these ‘ranj’ – ranjayati iti ragaha, ranjayati kriti-s as a cluster under the There is a reference to ‘dhwani- iti raktihi. That which is pleasing, category of ghana raga-s. Older visesha’ in this sloka from Brihaddcsi. which engages the mind joyfully texts record these five songs merely Scholars have suggested that may be called rakti. The term rakti dhwanivisesha may be taken th as Tyagaraja’ s compositions and is not found in pre-17 century not as the Pancharatna kriti-s. Not to connote sruti and that its texts like Niruktam, Vyjayanti and only are these raga-s unsuitable for integration with music ensures a Amarakosam. -

Analyzing the Melodic Structure of a Raga-Based Song
Georgian Electronic Scientific Journal: Musicology and Cultural Science 2009 | No.2(4) A Statistical Analysis Of A Raga-Based Song Soubhik Chakraborty1*, Ripunjai Kumar Shukla2, Kolla Krishnapriya3, Loveleen4, Shivee Chauhan5, Mona Kumari6, Sandeep Singh Solanki7 1, 2Department of Applied Mathematics, BIT Mesra, Ranchi-835215, India 3-7Department of Electronics and Communication Engineering, BIT Mesra, Ranchi-835215, India * email: [email protected] Abstract The origins of Indian classical music lie in the cultural and spiritual values of India and go back to the Vedic Age. The art of music was, and still is, regarded as both holy and heavenly giving not only aesthetic pleasure but also inducing a joyful religious discipline. Emotion and devotion are the essential characteristics of Indian music from the aesthetic side. From the technical perspective, we talk about melody and rhythm. A raga, the nucleus of Indian classical music, may be defined as a melodic structure with fixed notes and a set of rules characterizing a certain mood conveyed by performance.. The strength of raga-based songs, although they generally do not quite maintain the raga correctly, in promoting Indian classical music among laymen cannot be thrown away. The present paper analyzes an old and popular playback song based on the raga Bhairavi using a statistical approach, thereby extending our previous work from pure classical music to a semi-classical paradigm. The analysis consists of forming melody groups of notes and measuring the significance of these groups and segments, analysis of lengths of melody groups, comparing melody groups over similarity etc. Finally, the paper raises the question “What % of a raga is contained in a song?” as an open research problem demanding an in-depth statistical investigation. -
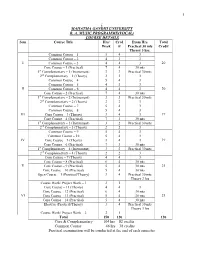
1 ; Mahatma Gandhi University B. A. Music Programme(Vocal
1 ; MAHATMA GANDHI UNIVERSITY B. A. MUSIC PROGRAMME(VOCAL) COURSE DETAILS Sem Course Title Hrs/ Cred Exam Hrs. Total Week it Practical 30 mts Credit Theory 3 hrs. Common Course – 1 5 4 3 Common Course – 2 4 3 3 I Common Course – 3 4 4 3 20 Core Course – 1 (Practical) 7 4 30 mts 1st Complementary – 1 (Instrument) 3 3 Practical 30 mts 2nd Complementary – 1 (Theory) 2 2 3 Common Course – 4 5 4 3 Common Course – 5 4 3 3 II Common Course – 6 4 4 3 20 Core Course – 2 (Practical) 7 4 30 mts 1st Complementary – 2 (Instrument) 3 3 Practical 30 mts 2nd Complementary – 2 (Theory) 2 2 3 Common Course – 7 5 4 3 Common Course – 8 5 4 3 III Core Course – 3 (Theory) 3 4 3 19 Core Course – 4 (Practical) 7 3 30 mts 1st Complementary – 3 (Instrument) 3 2 Practical 30 mts 2nd Complementary – 3 (Theory) 2 2 3 Common Course – 9 5 4 3 Common Course – 10 5 4 3 IV Core Course – 5 (Theory) 3 4 3 19 Core Course – 6 (Practical) 7 3 30 mts 1st Complementary – 4 (Instrument) 3 2 Practical 30 mts 2nd Complementary – 4 (Theory) 2 2 3 Core Course – 7 (Theory) 4 4 3 Core Course – 8 (Practical) 6 4 30 mts V Core Course – 9 (Practical) 5 4 30 mts 21 Core Course – 10 (Practical) 5 4 30 mts Open Course – 1 (Practical/Theory) 3 4 Practical 30 mts Theory 3 hrs Course Work/ Project Work – 1 2 1 Core Course – 11 (Theory) 4 4 3 Core Course – 12 (Practical) 6 4 30 mts VI Core Course – 13 (Practical) 5 4 30 mts 21 Core Course – 14 (Practical) 5 4 30 mts Elective (Practical/Theory) 3 4 Practical 30 mts Theory 3 hrs Course Work/ Project Work – 2 2 1 Total 150 120 120 Core & Complementary 104 hrs 82 credits Common Course 46 hrs 38 credits Practical examination will be conducted at the end of each semester 2 MAHATMA GANDHI UNIVERSITY B. -

Sanjay Subrahmanyan……………………………Revathi Subramony & Sanjana Narayanan
Table of Contents From the Publications & Outreach Committee ..................................... Lakshmi Radhakrishnan ............ 1 From the President’s Desk ...................................................................... Balaji Raghothaman .................. 2 Connect with SRUTI ............................................................................................................................ 4 SRUTI at 30 – Some reflections…………………………………. ........... Mani, Dinakar, Uma & Balaji .. 5 A Mellifluous Ode to Devi by Sikkil Gurucharan & Anil Srinivasan… .. Kamakshi Mallikarjun ............. 11 Concert – Sanjay Subrahmanyan……………………………Revathi Subramony & Sanjana Narayanan ..... 14 A Grand Violin Trio Concert ................................................................... Sneha Ramesh Mani ................ 16 What is in a raga’s identity – label or the notes?? ................................... P. Swaminathan ...................... 18 Saayujya by T.M.Krishna & Priyadarsini Govind ................................... Toni Shapiro-Phim .................. 20 And the Oscar goes to …… Kaapi – Bombay Jayashree Concert .......... P. Sivakumar ......................... 24 Saarangi – Harsh Narayan ...................................................................... Allyn Miner ........................... 26 Lec-Dem on Bharat Ratna MS Subbulakshmi by RK Shriramkumar .... Prabhakar Chitrapu ................ 28 Bala Bhavam – Bharatanatyam by Rumya Venkateshwaran ................. Roopa Nayak ......................... 33 Dr. M. Balamurali -
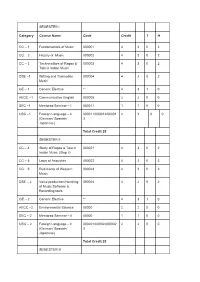
1 Fundamentals of Music 000001 4 3 0 2 CC
SEMESTER I Category Course Name Code Credit T H CC – 1 Fundamentals of Music 000001 4 3 0 2 CC – 2 History of Music 000002 4 3 0 2 CC – 3 Technicalities of Ragas & 000003 4 3 0 2 Tala in Indian Music DSE –1 Writing and Transcribe 000004 4 2 0 2 Music GE – 1 Generic Elective ** 4 3 1 0 AECC –1 Communicative English 000005 2 2 0 0 SEC –1 Mentored Seminar – I 000011 1 1 0 0 USC –1 Foreign Language – II 000011/000012/00001 2 2 0 0 (German/ Spanish/ 3 Japanese) Total Credit 25 SEMESTER II CC – 4 Study of Ragas & Tala in 000021 4 3 0 2 Indian Music (Step ii) CC – 5 Laws of Acoustics 000022 4 3 0 2 CC – 6 Rudiments of Western 000023 4 3 0 2 Music DSE – 2 Voice production/Handling 000024 4 2 0 2 of Music Software & Recording tools GE – 2 Generic Elective ** 4 3 1 0 AECC –2 Environmental Science 00000 2 2 0 0 SEC – 2 Mentored Seminar – II 00000 1 1 0 0 USC – 2 Foreign Language – II 000021/000022/00002 2 2 0 0 (German/ Spanish/ 3 Japanese) Total Credit 25 SEMESTER III CC – 7 Introduction to 000001 4 4 0 4 Contemporary Music CC – 8 Study of the Compositions 000002 5 3 0 2 of Tagore and other composers CC – 9 Audio and Sheet Music 000003 2 0 0 2 Discussion & Review CC – 10 Study on Theater Arts 000004 3 0 0 2 CC – 11 Study on Dance Arts 000005 3 4 0 4 DSE – 3 Film Music Appreciation & 000006 3 2 1 0 Review GE – 3 Generic Elective ** 4 3 1 0 SEC – 3 Mentored Seminar – III 000001 1 1 0 0 Total Credit 25 SEMESTER IV CC – 12 Demonstration of Ragas & 000011 4 3 1 0 Tala in Indian Music (Step iii) CC – 13 Mathematics of Music 000012 4 3 1 0 CC – 14 Overview -

Indian Traditional Grade 5
Foreword Welcome to the Musicea Arts and Culture Council Musicea Arts and Culture Council is a non-profit educational institution incorporated as a Section 8 Company of the Indian Companies Act, 2013. The primary objective of incorporation is to prepare curriculum, offer examinations, create career and jobs, recognise, award and honour achievements and promote young candidates in the field of music, dance, theatre, language, arts and sports. Musicea Arts and Culture Council is a college of national and international educators sharing the common dream of creating a world-class institution based in India to meet the requirements, demands and provide solutions to students and teachers. Musicea Arts and Culture Council have been formed to deliver an international standard grade-based music education system along with designing the national framework of music education in India. Several innovative and path-breaking measures implemented by the college council make it inclusive, holistic, and apt for 21st-century music education. The pioneering measures have already transformed the lives of thousands of educators and students and it is playing an active role in building a strong nation by assisting millions of aspiring students and teachers. Several initiatives are in place to protect, serve, and empower the teachers and students including a pension reward benefit. Musicea Arts and Culture Council have set benchmarks in creating international standard curriculum, offering examination, and performance, and by providing support, service, empowerment, inclusivity, decentralisation, growth, opportunity, career, finance, earnings, livelihood, award, reward and honour to thousands of teachers and students. Member teachers and students receive a series of direct benefits, honour and advantages from the Musicea Arts and Culture Council.