A Filament of Dark Matter Between Two Clusters of Galaxies
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

SDSS DR7 Superclusters Morphology
A&A 532, A5 (2011) Astronomy DOI: 10.1051/0004-6361/201116564 & c ESO 2011 Astrophysics SDSS DR7 superclusters Morphology M. Einasto1,L.J.Liivamägi1,2,E.Tago1,E.Saar1,E.Tempel1,2,J.Einasto1, V. J. Martínez3, and P. Heinämäki4 1 Tartu Observatory, 61602 Tõravere, Estonia e-mail: [email protected] 2 Institute of Physics, Tartu University, Tähe 4, 51010 Tartu, Estonia 3 Observatori Astronòmic, Universitat de València, Apartat de Correus 22085, 46071 València, Spain 4 Tuorla Observatory, University of Turku, Väisäläntie 20, Piikkiö, Finland Received 24 January 2011 / Accepted 2 May 2011 ABSTRACT Aims. We study the morphology of a set of superclusters drawn from the SDSS DR7. Methods. We calculate the luminosity density field to determine superclusters from a flux-limited sample of galaxies from SDSS DR7 and select superclusters with 300 and more galaxies for our study. We characterise the morphology of superclusters using the fourth Minkowski functional V3, the morphological signature (the curve in the shapefinder’s K1-K2 plane) and the shape parameter (the ratio of the shapefinders K1/K2). We investigate the supercluster sample using multidimensional normal mixture modelling. We use Abell clusters to identify our superclusters with known superclusters and to study the large-scale distribution of superclusters. Results. The superclusters in our sample form three chains of superclusters; one of them is the Sloan Great Wall. Most superclusters have filament-like overall shapes. Superclusters can be divided into two sets; more elongated superclusters are more luminous, richer, have larger diameters and a more complex fine structure than less elongated superclusters. The fine structure of superclusters can be divided into four main morphological types: spiders, multispiders, filaments, and multibranching filaments. -

The X-Ray Universe 2011
THE X-RAY UNIVERSE 2011 27 - 30 June 2011 Berlin, Germany A conference organised by the XMM-Newton Science Operations Centre, European Space Astronomy Centre (ESAC), European Space Agency (ESA) ABSTRACT BOOK Oral Communications and Posters Edited by Andy Pollock with the help of Matthias Ehle, Cristina Hernandez, Jan-Uwe Ness, Norbert Schartel and Martin Stuhlinger Organising Committees Scientific Organising Committee Giorgio Matt (Universit`adegli Studi Roma Tre, Italy) Chair Norbert Schartel (XMM-Newton SOC, Madrid, ESA) Co-Chair M. Ali Alpar (Sabanci University, Istanbul, Turkey) Didier Barret (Centre d’Etude Spatiale des Rayonnements, Toulouse, France) Ehud Behar (Technion Israel Institute of Technology, Haifa, Israel) Hans B¨ohringer (MPE, Garching, Germany) Graziella Branduardi-Raymont (University College London-MSSL, Dorking, UK) Francisco J. Carrera (Instituto de F´ısicade Cantabria, Santander, Spain) Finn E. Christensen (Danmarks Tekniske Universitet, Copenhagen, Denmark) Anne Decourchelle (Commissariat `al’´energie atomique et aux ´energies alternatives, Saclay, France) Jan-Willem den Herder (SRON, Utrecht, The Netherlands) Rosario Gonzalez-Riestra (XMM-Newton SOC, Madrid, ESA) Coel Hellier (Keele University, UK) Stefanie Komossa (MPE, Garching, Germany) Chryssa Kouveliotou (NASA/Marshall Space Flight Center, Huntsville, Alabama, USA) Kazuo Makishima (University of Tokyo, Japan) Sera Markoff (University of Amsterdam, The Netherlands) Brian McBreen (University College Dublin, Ireland) Brian McNamara (University of Waterloo, Canada) -

Weak Lensing Galaxy Cluster Field Reconstruction
Mon. Not. R. Astron. Soc. 000, 1–12 (2012) Printed 14 October 2018 (MN LATEX style file v2.2) Weak Lensing Galaxy Cluster Field Reconstruction E. Jullo1, S. Pires2, M. Jauzac3 & J.-P. Kneib4;1 1Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388, Marseille, France 2Laboratoire AIM, CEA/DSM-CNRS, Université Paris 7 Diderot, IRFU/SAp-SEDI, Service d’Astrophysique, CEA Saclay, Orme des Merisiers, 91191 Gif-sur-Yvette, France 3Astrophysics and Cosmology Research Unit, School of Mathematical Sciences, University of KwaZulu-Natal, Durban 4041, South Africa 4LASTRO, Ecole polytechnique fédérale de Lausanne, Suisse Released 2013 Xxxxx XX ABSTRACT In this paper, we compare three methods to reconstruct galaxy cluster density fields with weak lensing data. The first method called FLens integrates an inpainting concept to invert the shear field with possible gaps, and a multi-scale entropy denoising proce- dure to remove the noise contained in the final reconstruction, that arises mostly from the random intrinsic shape of the galaxies. The second and third methods are based on a model of the density field made of a multi-scale grid of radial basis functions. In one case, the model parameters are computed with a linear inversion involving a singular value decomposition. In the other case, the model parameters are estimated using a Bayesian MCMC optimization implemented in the lensing software Lenstool. Methods are compared on simulated data with varying galaxy density fields. We pay particular attention to the errors estimated with resampling. We find the multi-scale grid model optimized with MCMC to provide the best results, but at high computational cost, especially when considering resampling. -

An Outline of Stellar Astrophysics with Problems and Solutions
An Outline of Stellar Astrophysics with Problems and Solutions Using Maple R and Mathematica R Robert Roseberry 2016 1 Contents 1 Introduction 5 2 Electromagnetic Radiation 7 2.1 Specific intensity, luminosity and flux density ............7 Problem 1: luminous flux (**) . .8 Problem 2: galaxy fluxes (*) . .8 Problem 3: radiative pressure (**) . .9 2.2 Magnitude ...................................9 Problem 4: magnitude (**) . 10 2.3 Colour ..................................... 11 Problem 5: Planck{Stefan-Boltzmann{Wien{colour (***) . 13 Problem 6: Planck graph (**) . 13 Problem 7: radio and visual luminosity and brightness (***) . 14 Problem 8: Sirius (*) . 15 2.4 Emission Mechanisms: Continuum Emission ............. 15 Problem 9: Orion (***) . 17 Problem 10: synchrotron (***) . 18 Problem 11: Crab (**) . 18 2.5 Emission Mechanisms: Line Emission ................. 19 Problem 12: line spectrum (*) . 20 2.6 Interference: Line Broadening, Scattering, and Zeeman splitting 21 Problem 13: natural broadening (**) . 21 Problem 14: Doppler broadening (*) . 22 Problem 15: Thomson Cross Section (**) . 23 Problem 16: Inverse Compton scattering (***) . 24 Problem 17: normal Zeeman splitting (**) . 25 3 Measuring Distance 26 3.1 Parallax .................................... 27 Problem 18: parallax (*) . 27 3.2 Doppler shifting ............................... 27 Problem 19: supernova distance (***) . 28 3.3 Spectroscopic parallax and Main Sequence fitting .......... 28 Problem 20: Main Sequence fitting (**) . 29 3.4 Standard candles ............................... 30 Video: supernova light curve . 30 Problem 21: Cepheid distance (*) . 30 3.5 Tully-Fisher relation ............................ 31 3.6 Lyman-break galaxies and the Hubble flow .............. 33 4 Transparent Gas: Interstellar Gas Clouds and the Atmospheres and Photospheres of Stars 35 2 4.1 Transfer equation and optical depth .................. 36 Problem 22: optical depth (**) . 37 4.2 Plane-parallel atmosphere, Eddington's approximation, and limb darkening .................................. -

Remembering Bill Bogardus Photographing the Moon
Published by the Astronomical League Vol. 71, No. 2 March 2019 REMEMBERING BILL BOGARDUS PHOTOGRAPHING THE MOON 7.20.69 5 YEARS TREASURES OF THE LINDA HALL LIBRARY APOLLO 11 THE COSMIC WEB ONOMY T STR O T A H G E N P I E Contents G O N P I L R E B 4 . Reflector Mail ASTRONOMY DAY Join a Tour This Year! 4 . President’s Corner May 11 & 5 . International Dark-Sky Association From 37,000 feet above the Pacific Total Eclipse Flight: Chile October 5, 2019 6 . Night Sky Network Ocean, you’ll be high above any clouds, July 2, 2019 For a FREE 76-page seeing up to 3¼ minutes of totality in a dark sky that makes the Sun’s corona look 6 . Deep-Sky Objects Astronomy Day Handbook incredibly dramatic. Our flight will de- full of ideas and suggestions, part from and return to Santiago, Chile. 9 . Remembering Bill Bogardus skyandtelescope.com/2019eclipseflight go to: 10 . From Around the League www.astroleague.org Click on "Astronomy Day” African Stargazing Safari Join astronomer Stephen James PAGE 19 13 . Observing Awards Scroll down to "Free O’Meara in wildlife-rich Botswana July 29–August 4, 2019 Astronomy Day Handbook" for evening stargazing and daytime 14 . Basic Small-Scope Lunar Imaging safari drives at three luxury field For more information, contact: camps. Only 16 spaces available! 18 . The Vault of Heaven – Gary Tomlinson Optional extension to Victoria Falls. ̨̨̨̨̨̨̨̨̨̨̨̨̨̨̨Treasures of the Linda Hall Library Astronomy Day Coordinator skyandtelescope.com/botswana2019 [email protected] 24 . The Cosmic Web Iceland Aurorae 27 . -

Is the Butcher-Oemler Effect a Function of the Cluster Redshift? S. Andreon
THE ASTROPHYSICAL JOURNAL, 516:647È659, 1999 May 10 ( 1999. The American Astronomical Society. All rights reserved. Printed in U.S.A. IS THE BUTCHER-OEMLER EFFECT A FUNCTION OF THE CLUSTER REDSHIFT? S. ANDREON Osservatorio Astronomico di Capodimonte, via Moiariello 16, 80131 Napoli, Italy; andreon=na.astro.it AND S. ETTORI Institute of Astronomy, Madingley Road, Cambridge CB3 0HA, England, UK; settori=ast.cam.ac.uk Received 1998 May 29; accepted 1998 December 18 ABSTRACT Using PSPC ROSAT data, we measure the X-ray surface brightness proÐles, size, and luminosity of the Butcher-Oemler (BO) sample of clusters of galaxies. The cluster X-ray size, as measured by the Pet- rosianrg/2 radius, does not change with redshift and is independent of X-ray luminosity. On the other hand, the X-ray luminosity increases with redshift. Considering that fair samples show no evolution, or negative luminosity evolution, we conclude that the BO sample is not formed from the same class of objects observed at di†erent look-back times. This is in conÑict with the usual interpretation of the Butcher-Oemler as an evolutionary (or redshift dependent) e†ect, based on the assumption that we are comparing the same class of objects at di†erent redshifts. Other trends present in the BO sample reÑect selection criteria rather than di†erences in look-back time, as independently conÐrmed by the fact that trends lose strength when we enlarge the sample with an X-rayÈselected sample of clusters. The variety of optical sizes and shapes of the clusters in the Butcher-Oemler sample and the Malmquist-like bias are the reasons for these selection e†ects that mimic the trends usually interpreted as changes due to evolu- tion. -

And Ecclesiastical Cosmology
GSJ: VOLUME 6, ISSUE 3, MARCH 2018 101 GSJ: Volume 6, Issue 3, March 2018, Online: ISSN 2320-9186 www.globalscientificjournal.com DEMOLITION HUBBLE'S LAW, BIG BANG THE BASIS OF "MODERN" AND ECCLESIASTICAL COSMOLOGY Author: Weitter Duckss (Slavko Sedic) Zadar Croatia Pусскй Croatian „If two objects are represented by ball bearings and space-time by the stretching of a rubber sheet, the Doppler effect is caused by the rolling of ball bearings over the rubber sheet in order to achieve a particular motion. A cosmological red shift occurs when ball bearings get stuck on the sheet, which is stretched.“ Wikipedia OK, let's check that on our local group of galaxies (the table from my article „Where did the blue spectral shift inside the universe come from?“) galaxies, local groups Redshift km/s Blueshift km/s Sextans B (4.44 ± 0.23 Mly) 300 ± 0 Sextans A 324 ± 2 NGC 3109 403 ± 1 Tucana Dwarf 130 ± ? Leo I 285 ± 2 NGC 6822 -57 ± 2 Andromeda Galaxy -301 ± 1 Leo II (about 690,000 ly) 79 ± 1 Phoenix Dwarf 60 ± 30 SagDIG -79 ± 1 Aquarius Dwarf -141 ± 2 Wolf–Lundmark–Melotte -122 ± 2 Pisces Dwarf -287 ± 0 Antlia Dwarf 362 ± 0 Leo A 0.000067 (z) Pegasus Dwarf Spheroidal -354 ± 3 IC 10 -348 ± 1 NGC 185 -202 ± 3 Canes Venatici I ~ 31 GSJ© 2018 www.globalscientificjournal.com GSJ: VOLUME 6, ISSUE 3, MARCH 2018 102 Andromeda III -351 ± 9 Andromeda II -188 ± 3 Triangulum Galaxy -179 ± 3 Messier 110 -241 ± 3 NGC 147 (2.53 ± 0.11 Mly) -193 ± 3 Small Magellanic Cloud 0.000527 Large Magellanic Cloud - - M32 -200 ± 6 NGC 205 -241 ± 3 IC 1613 -234 ± 1 Carina Dwarf 230 ± 60 Sextans Dwarf 224 ± 2 Ursa Minor Dwarf (200 ± 30 kly) -247 ± 1 Draco Dwarf -292 ± 21 Cassiopeia Dwarf -307 ± 2 Ursa Major II Dwarf - 116 Leo IV 130 Leo V ( 585 kly) 173 Leo T -60 Bootes II -120 Pegasus Dwarf -183 ± 0 Sculptor Dwarf 110 ± 1 Etc. -

Astronomy 422
Astronomy 422 Lecture 15: Expansion and Large Scale Structure of the Universe Key concepts: Hubble Flow Clusters and Large scale structure Gravitational Lensing Sunyaev-Zeldovich Effect Expansion and age of the Universe • Slipher (1914) found that most 'spiral nebulae' were redshifted. • Hubble (1929): "Spiral nebulae" are • other galaxies. – Measured distances with Cepheids – Found V=H0d (Hubble's Law) • V is called recessional velocity, but redshift due to stretching of photons as Universe expands. • V=H0D is natural result of uniform expansion of the universe, and also provides a powerful distance determination method. • However, total observed redshift is due to expansion of the universe plus a galaxy's motion through space (peculiar motion). – For example, the Milky Way and M31 approaching each other at 119 km/s. • Hubble Flow : apparent motion of galaxies due to expansion of space. v ~ cz • Cosmological redshift: stretching of photon wavelength due to expansion of space. Recall relativistic Doppler shift: Thus, as long as H0 constant For z<<1 (OK within z ~ 0.1) What is H0? Main uncertainty is distance, though also galaxy peculiar motions play a role. Measurements now indicate H0 = 70.4 ± 1.4 (km/sec)/Mpc. Sometimes you will see For example, v=15,000 km/s => D=210 Mpc = 150 h-1 Mpc. Hubble time The Hubble time, th, is the time since Big Bang assuming a constant H0. How long ago was all of space at a single point? Consider a galaxy now at distance d from us, with recessional velocity v. At time th ago it was at our location For H0 = 71 km/s/Mpc Large scale structure of the universe • Density fluctuations evolve into structures we observe (galaxies, clusters etc.) • On scales > galaxies we talk about Large Scale Structure (LSS): – groups, clusters, filaments, walls, voids, superclusters • To map and quantify the LSS (and to compare with theoretical predictions), we use redshift surveys. -

Monthly Newsletter of the Durban Centre - March 2018
Page 1 Monthly Newsletter of the Durban Centre - March 2018 Page 2 Table of Contents Chairman’s Chatter …...…………………….……….………..….…… 3 Andrew Gray …………………………………………...………………. 5 The Hyades Star Cluster …...………………………….…….……….. 6 At the Eye Piece …………………………………………….….…….... 9 The Cover Image - Antennae Nebula …….……………………….. 11 Galaxy - Part 2 ….………………………………..………………….... 13 Self-Taught Astronomer …………………………………..………… 21 The Month Ahead …..…………………...….…….……………..…… 24 Minutes of the Previous Meeting …………………………….……. 25 Public Viewing Roster …………………………….……….…..……. 26 Pre-loved Telescope Equipment …………………………...……… 28 ASSA Symposium 2018 ………………………...……….…......…… 29 Member Submissions Disclaimer: The views expressed in ‘nDaba are solely those of the writer and are not necessarily the views of the Durban Centre, nor the Editor. All images and content is the work of the respective copyright owner Page 3 Chairman’s Chatter By Mike Hadlow Dear Members, The third month of the year is upon us and already the viewing conditions have been more favourable over the last few nights. Let’s hope it continues and we have clear skies and good viewing for the next five or six months. Our February meeting was well attended, with our main speaker being Dr Matt Hilton from the Astrophysics and Cosmology Research Unit at UKZN who gave us an excellent presentation on gravity waves. We really have to be thankful to Dr Hilton from ACRU UKZN for giving us his time to give us presentations and hope that we can maintain our relationship with ACRU and that we can draw other speakers from his colleagues and other research students! Thanks must also go to Debbie Abel and Piet Strauss for their monthly presentations on NASA and the sky for the following month, respectively. -

X-Ray Calibration of SZ Scaling Relations with the ACCEPT
Mon. Not. R. Astron. Soc. 000, 1–10 (2011) Printed 11 October 2018 (MN LATEX style file v2.2) X-ray calibration of SZ scaling relations with the ACCEPT catalogue of galaxy clusters observed by Chandra B. Comis1⋆, M. De Petris1, A. Conte1, L. Lamagna1 and S. De Gregori1 1Sapienza University of Rome, Department of Physics, P.le A. Moro, 2 Rome, Italy Accepted for publication in MNRAS ABSTRACT We explore the scaling relation between the flux of the Sunyaev-Zel’dovich (SZ) ef- fect and the total mass of galaxy clusters using already reduced Chandra X-ray data present in the ACCEPT (Archive of Chandra Cluster Entropy Profile Tables) cata- logue. The analysis is conducted over a sample of 226 objects, examining the relatively small scale corresponding to a cluster overdensity equal to 2500 times the critical density of the background universe, at which the total masses have been calculated exploiting the hydrostatic equilibrium hypothesis. Core entropy (K0) is strongly corre- lated with the central cooling time, and is therefore used to identify cooling-core (CC) objects in our sample. Our results confirm the self-similarity of the scaling relation between the integrated Comptonization parameter (Y ) and the cluster mass, for both CC and NCC (non-cooling-core) clusters. The consistency of our calibration with re- cent ones has been checked, with further support for Y as a good mass proxy. We also investigate the robustness of the constant gas fraction assumption, for fixed overden- sity, and of the YX proxy (Kravtsov et al. 2007) considering CC and NCC clusters, again sorted on K0 from our sample. -

The Nanograv 11 Yr Data Set: Limits on Supermassive Black Hole Binaries in Galaxies Within 500 Mpc
The Astrophysical Journal, 914:121 (15pp), 2021 June 20 https://doi.org/10.3847/1538-4357/abfcd3 © 2021. The American Astronomical Society. All rights reserved. The NANOGrav 11 yr Data Set: Limits on Supermassive Black Hole Binaries in Galaxies within 500 Mpc Zaven Arzoumanian1, Paul T. Baker2 , Adam Brazier3, Paul R. Brook4,5 , Sarah Burke-Spolaor4,5 , Bence Becsy6 , Maria Charisi7,8,38 , Shami Chatterjee3 , James M. Cordes3 , Neil J. Cornish6 , Fronefield Crawford9 , H. Thankful Cromartie10 , Megan E. DeCesar11 , Paul B. Demorest12 , Timothy Dolch13,14 , Rodney D. Elliott15 , Justin A. Ellis16, Elizabeth C. Ferrara17 , Emmanuel Fonseca18 , Nathan Garver-Daniels4,5 , Peter A. Gentile4,5 , Deborah C. Good19 , Jeffrey S. Hazboun20 , Kristina Islo21, Ross J. Jennings3 , Megan L. Jones21 , Andrew R. Kaiser4,5 , David L. Kaplan21 , Luke Zoltan Kelley22 , Joey Shapiro Key20 , Michael T. Lam23,24 , T. Joseph W. Lazio7,25, Jing Luo26 , Ryan S. Lynch27 , Chung-Pei Ma28 , Dustin R. Madison4,5,39 , Maura A. McLaughlin4,5 , Chiara M. F. Mingarelli29,30 , Cherry Ng31 , David J. Nice11 , Timothy T. Pennucci32,33,40 , Nihan S. Pol4,5,8 , Scott M. Ransom32 , Paul S. Ray34 , Brent J. Shapiro-Albert4,5 , Xavier Siemens21,35 , Joseph Simon7,25 , Renée Spiewak36 , Ingrid H. Stairs19 , Daniel R. Stinebring37 , Kevin Stovall12 , Joseph K. Swiggum11,41 , Stephen R. Taylor8 , Michele Vallisneri7,25 , Sarah J. Vigeland21 , and Caitlin A. Witt4,5 The NANOGrav Collaboration 1 X-Ray Astrophysics Laboratory, NASA Goddard Space Flight Center, Code 662, Greenbelt, MD 20771, USA 2 Department of Physics and Astronomy, Widener University, One University Place, Chester, PA 19013, USA 3 Cornell Center for Astrophysics and Planetary Science and Department of Astronomy, Cornell University, Ithaca, NY 14853, USA 4 Department of Physics and Astronomy, West Virginia University, P.O. -
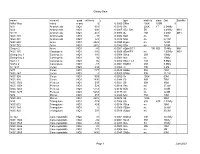
Galaxy Data Name Constell
Galaxy Data name constell. quadvel km/s z type width ly starsDist. Satellite Milky Way many many 0 0.0000 SBbc 106K 200M 0 M31 Andromeda NQ1 -301 -0.0010 SA 220K 1T 2.54Mly M32 Andromeda NQ1 -200 -0.0007 cE2 Sat. 5K 2.49Mly M31 M110 Andromeda NQ1 -241 -0.0008 dE 15K 2.69M M31 NGC 404 Andromeda NQ1 -48 -0.0002 SA0 no 10M NGC 891 Andromeda NQ1 528 0.0018 SAb no 27.3M NGC 680 Aries NQ1 2928 0.0098 E pec no 123M NGC 772 Aries NQ1 2472 0.0082 SAb no 130M Segue 2 Aries NQ1 -40 -0.0001 dSph/GC?. 100 5E5 114Kly MW NGC 185 Cassiopeia NQ1 -185 -0.0006dSph/E3 no 2.05Mly M31 Dwingeloo 1 Cassiopeia NQ1 110 0.0004 SBcd 25K 10Mly Dwingeloo 2 Cassiopeia NQ1 94 0.0003Iam no 10Mly Maffei 1 Cassiopeia NQ1 66 0.0002 S0pec E3 75K 9.8Mly Maffei 2 Cassiopeia NQ1 -17 -0.0001 SABbc 25K 9.8Mly IC 1613 Cetus NQ1 -234 -0.0008Irr 10K 2.4M M77 Cetus NQ1 1177 0.0039 SABd 95K 40M NGC 247 Cetus NQ1 0 0.0000SABd 50K 11.1M NGC 908 Cetus NQ1 1509 0.0050Sc 105K 60M NGC 936 Cetus NQ1 1430 0.0048S0 90K 75M NGC 1023 Perseus NQ1 637 0.0021 S0 90K 36M NGC 1058 Perseus NQ1 529 0.0018 SAc no 27.4M NGC 1263 Perseus NQ1 5753 0.0192SB0 no 250M NGC 1275 Perseus NQ1 5264 0.0175cD no 222M M74 Pisces NQ1 857 0.0029 SAc 75K 30M NGC 488 Pisces NQ1 2272 0.0076Sb 145K 95M M33 Triangulum NQ1 -179 -0.0006 SA 60K 40B 2.73Mly NGC 672 Triangulum NQ1 429 0.0014 SBcd no 16M NGC 784 Triangulum NQ1 0 0.0000 SBdm no 26.6M NGC 925 Triangulum NQ1 553 0.0018 SBdm no 30.3M IC 342 Camelopardalis NQ2 31 0.0001 SABcd 50K 10.7Mly NGC 1560 Camelopardalis NQ2 -36 -0.0001Sacd 35K 10Mly NGC 1569 Camelopardalis NQ2 -104 -0.0003Ibm 5K 11Mly NGC 2366 Camelopardalis NQ2 80 0.0003Ibm 30K 10M NGC 2403 Camelopardalis NQ2 131 0.0004Ibm no 8M NGC 2655 Camelopardalis NQ2 1400 0.0047 SABa no 63M Page 1 2/28/2020 Galaxy Data name constell.