SPH Simulations of Clumps Formation by Dissipative Collisions of Molecular Clouds
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1St First Society Handbook AFB Album of Favorite Barber Shop Ballads, Old and Modern
1st First Society Handbook AFB Album of Favorite Barber Shop Ballads, Old and Modern. arr. Ozzie Westley (1944) BPC The Barberpole Cat Program and Song Book. (1987) BB1 Barber Shop Ballads: a Book of Close Harmony. ed. Sigmund Spaeth (1925) BB2 Barber Shop Ballads and How to Sing Them. ed. Sigmund Spaeth. (1940) CBB Barber Shop Ballads. (Cole's Universal Library; CUL no. 2) arr. Ozzie Westley (1943?) BC Barber Shop Classics ed. Sigmund Spaeth. (1946) BH Barber Shop Harmony: a Collection of New and Old Favorites For Male Quartets. ed. Sigmund Spaeth. (1942) BM1 Barber Shop Memories, No. 1, arr. Hugo Frey (1949) BM2 Barber Shop Memories, No. 2, arr. Hugo Frey (1951) BM3 Barber Shop Memories, No. 3, arr, Hugo Frey (1975) BP1 Barber Shop Parade of Quartet Hits, no. 1. (1946) BP2 Barber Shop Parade of Quartet Hits, no. 2. (1952) BP Barbershop Potpourri. (1985) BSQU Barber Shop Quartet Unforgettables, John L. Haag (1972) BSF Barber Shop Song Fest Folio. arr. Geoffrey O'Hara. (1948) BSS Barber Shop Songs and "Swipes." arr. Geoffrey O'Hara. (1946) BSS2 Barber Shop Souvenirs, for Male Quartets. New York: M. Witmark (1952) BOB The Best of Barbershop. (1986) BBB Bourne Barbershop Blockbusters (1970) BB Bourne Best Barbershop (1970) CH Close Harmony: 20 Permanent Song Favorites. arr. Ed Smalle (1936) CHR Close Harmony: 20 Permanent Song Favorites. arr. Ed Smalle. Revised (1941) CH1 Close Harmony: Male Quartets, Ballads and Funnies with Barber Shop Chords. arr. George Shackley (1925) CHB "Close Harmony" Ballads, for Male Quartets. (1952) CHS Close Harmony Songs (Sacred-Secular-Spirituals - arr. -

Contextual Predictability Norms for Pairs of Words Differing in a Single Letter
H I LLINI S UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN PRODUCTION NOTE University of Illinois at Urbana-Champaign Library Large-scale Digitization Project, 2007. ~66' Technical Report No. 260 CONTEXTUAL PREDICTABILITY NORMS FOR PAIRS OF WORDS DIFFERING IN A SINGLE LETTER Harry E. Blanchard, George W. McConkie and David Zola University of Illinois at Urbana-Champaign August 1982 Center for the Study of Reading TECHNICAL REPORTS UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN 51 Gerty Drive Champaign, Illinois 61820 BOLT BERANEK AND NEWMAN INC. 50 Moulton Street Cambridge, Massachusetts 02238 [LtHE LIBRARY OF TH-I The National Institute of Education U.S. Department of Education UNIVE.SITY OF ILL:S Washington. D.C. 20208 IT ^a -- CENTER FOR THE STUDY OF READING Technical Report No. 260 CONTEXTUAL PREDICTABILITY' NORMS FOR PAIRS OF WORDS DIFFERING IN A SINGLE LETTER Harry E. Blanchard, George W. McConkie and David Zola University of Illinois at Urbana-Champaign August 1982 University of Illinois at Urbana-Champaign Bolt Beranek and Newman Inc. 51 Gerty Drive 50 Moulton Street Champaign, Illinois 61820. Cambridge, Massachusetts 02238 This research was conducted under grants MH 32884 and MH 33408 from the National Institute of Mental Health to the first author, and National Institute of Education contract HEW-NIE-C-400-76-0116 to the Center for the Study of Reading. Copies of this report can be obtained by writing to George W. McConkie, Center for the Study of Reading, 51 Gerty Drive, Champaign, Illinois 61820. EDITORIAL BOARD William Nagy and Stephen Wilhite Co--Editors Harry Blanchard Anne Hay Charlotte Blomeyer Asghar Iran-Nejad Nancy Bryant Margi Laff Avon Crismore Terence Turner Meg Sallagher Paul Wilson Abstract Predictability Norms Four hundred sixty-seven pairs of short texts were written. -

Open Steinle Cory Kanyecriticism.Pdf
THE PENNSYLVANIA STATE UNIVERSITY SCHREYER HONORS COLLEGE DEPARTMENT OF COMMUNICATION ARTS & SCIENCES “I THOUGHT ABOUT KILLING YOU”: CONSIDERING THE UTILITY OF RHETORICAL AND BIOGRAPHICAL CRITICAL APPROACHES TO KANYE WEST’S YE CORY N. STEINLE SPRING 2020 A thesis submitted in partial fulfillment of the requirements for baccalaureate degrees in Communication Arts and Sciences and Labor and Employment Relations with honors in Communication Arts and Sciences Reviewed and approved* by the following: Bradford Vivian Professor of Communication Arts & Sciences Thesis Supervisor Lori Bedell Associate Teaching Professor in Communication Arts & Sciences Honors Adviser * Signatures are on file in the Schreyer Honors College. i ABSTRACT This paper examines the merits of intrinsic and extrinsic critical approaches to hip-hop artifacts. To do so, I provide both a neo-Aristotelian and biographical criticism of three songs from ye (2018) by Kanye West. Chapters 1 & 2 consider Roland Barthes’ The Death of the Author and other landmark papers in rhetorical and literary theory to develop an intrinsic and extrinsic approach to criticizing ye (2018), evident in Tables 1 & 2. Chapter 3 provides the biographical antecedents of West’s life prior to the release of ye (2018). Chapters 4, 5, & 6 supply intrinsic (neo-Aristotelian) and extrinsic (biographical) critiques of the selected artifacts. Each of these chapters aims to address the concerns of one of three guiding questions: which critical approaches prove most useful to the hip-hop consumer listening to this song? How can and should the listener construct meaning? Are there any improper ways to critique and interpret this song? Chapter 7 discusses the variance in each mode of critical analysis from Chapters 4, 5, & 6. -

Download Nf Flac Album Download Nf Flac Album
download nf flac album Download nf flac album. Completing the CAPTCHA proves you are a human and gives you temporary access to the web property. What can I do to prevent this in the future? If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware. If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices. Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store. Cloudflare Ray ID: 67a5889e8ff5f16a • Your IP : 188.246.226.140 • Performance & security by Cloudflare. NF Clouds (The Mixtape) Full Album Download. NF - Clouds (The Mixtape) Album DownloadCLOUDS (THE MIXTAPE) of new songs music track from NF first appearence on 2021-03-26. It has a Hip-Hop/Rap genre and very popular in USA. CLOUDS (THE MIXTAPE) was released under part of ℗ 2021 NF Real Music, LLC. You can preview and listen CLOUDS (THE MIXTAPE) tracks before purchasing and download online. If you are looking for CLOUDS (THE MIXTAPE) containing lyrics for captions from NF, you will not find it here. We only preview track as a sample. You can browse other website to find NF - CLOUDS (THE MIXTAPE) lyrics. >> DOWNLOAD NOW << TRUST ft. Tech N9ne. Download NF CLOUDS [THE MIXTAPE] EP Album Zip File Download for free mp3 NF - CLOUDS (THE MIXTAPE) zip mega torrent zippyshare. -

4Th Grade Inclement Weather Make-Up Materials – All Subjects
4th Grade Inclement Weather Make-up Materials – All Subjects Click on the title or link in the “Online Learning Support and Activities” column to review all online resources. Focus Standards: Provide additional time and Online Learning Supporting Standard opportunity with these Support and Activities standards. ELACC4RL1: Refer to details ELACC4RI1: Refer to Choose a story to practice and examples in a text when details and examples in a reading comprehension. explaining what the text says text when explaining what explicitly and when drawing the text says explicitly and Good Readers Look for Clues inferences from the text. when drawing inferences from the text. Good Readers Look for Clues; Practice Inference Game Inferencing Looking for Clues What Can you Infer? ELACC4RL2: Determine a ELACC4RI2: Determine the Identifying Topics and Main Ideas theme of a story, drama, or main idea of a text and poem from details in the text; explain how it is supported Line Breaker summarize the text. by key details; summarize the text. Main Idea; Battleship Theme Poems Theme Poetry ELACC4RL3: Describe in ELACC4RI3: Explain Bon Appetite depth a character, setting, or events, procedures, ideas, event in a story or drama, or concepts in a historical, Good Readers Look for Clues drawing on specific details in scientific, or technical text, the text (e.g., a character’s including what happened Good Readers Look for Clues; thoughts, words, or actions). and why, based on specific Practice information in the text. Inference Game Seven Common Character Types ELACC4RL4: Determine the ELACC4RI4: Determine the Derive Meaning from Words and meaning of words and meaning of general Phrases phrases as they are used in a academic language and text, including those that domain-specific words or It Came from Greek Mythology allude to significant phrases in a text relevant to characters found in mythology a grade 4 topic or subject Practice Word Meanings (e.g., Herculean). -

Proquest Dissertations
Library and Archives Bibliotheque et l+M Canada Archives Canada Published Heritage Direction du Branch Patrimoine de I'edition 395 Wellington Street 395, rue Wellington Ottawa ON K1A 0N4 Ottawa ON K1A 0N4 Canada Canada Your file Votre reference ISBN: 978-0-494-54229-3 Our file Notre reference ISBN: 978-0-494-54229-3 NOTICE: AVIS: The author has granted a non L'auteur a accorde une licence non exclusive exclusive license allowing Library and permettant a la Bibliotheque et Archives Archives Canada to reproduce, Canada de reproduire, publier, archiver, publish, archive, preserve, conserve, sauvegarder, conserver, transmettre au public communicate to the public by par telecommunication ou par I'lnternet, preter, telecommunication or on the Internet, distribuer et vendre des theses partout dans le loan, distribute and sell theses monde, a des fins commerciales ou autres, sur worldwide, for commercial or non support microforme, papier, electronique et/ou commercial purposes, in microform, autres formats. paper, electronic and/or any other formats. The author retains copyright L'auteur conserve la propriete du droit d'auteur ownership and moral rights in this et des droits moraux qui protege cette these. Ni thesis. Neither the thesis nor la these ni des extraits substantiels de celle-ci substantial extracts from it may be ne doivent etre imprimes ou autrement printed or otherwise reproduced reproduits sans son autorisation. without the author's permission. In compliance with the Canadian Conformement a la loi canadienne sur la Privacy Act some supporting forms protection de la vie privee, quelques may have been removed from this formulaires secondaires ont ete enleves de thesis. -

Observation of Cirrus Clouds with GLORIA During the WISE Campaign
https://doi.org/10.5194/amt-2020-394 Preprint. Discussion started: 26 October 2020 c Author(s) 2020. CC BY 4.0 License. Observation of Cirrus Clouds with GLORIA during the WISE Campaign: Detection Methods and Cirrus Characterization Irene Bartolome Garcia1, Reinhold Spang1, Jörn Ungermann1, Sabine Griessbach2, Martina Krämer1, Michael Höpfner3, and Martin Riese1 1Institute für Energie and Klimaforschung (IEK-7), Forschungszentrum Jülich GmbH, 52428 Jülich, Germany 2Jülich Supercomputing Centre (JSC), Forschungszentrum Jülich GmbH, 52428 Jülich, Germany 3Institute of Meteorology and Climate Research, Karlsruhe Institute of Technology, 76021 Karlsruhe, Germany Correspondence: Irene Bartolome Garcia ([email protected]) Abstract. Cirrus clouds contribute to the general radiation budget of the Earth, playing an important role in climate projections. Of special interest are optically thin cirrus clouds close to the tropopause due to the fact that their impact is not yet well understood. Measuring these clouds is challenging as both high spatial resolution as well as a very high detection sensitivity are needed. These criteria are fulfilled by the infrared limb sounder GLORIA (Gimballed Limb Observer for Radiance Imaging of 5 the Atmosphere). This study presents a characterization of observed cirrus clouds using the data obtained by GLORIA aboard the German research aircraft HALO during the WISE (Wave-driven ISentropic Exchange) campaign in September/October 2017. We developed an optimized cloud detection method and derived macro-physical characteristics of the detected cirrus clouds such as cloud top height, cloud top bottom height, vertical extent and cloud top position with respect to the tropopause. The fraction of cirrus clouds detected above the tropopause is in the order of 13 % to 27 %. -

Lost Languages of the Peruvian North Coast LOST LANGUAGES LANGUAGES LOST
12 Lost Languages of the Peruvian North Coast LOST LANGUAGES LANGUAGES LOST ESTUDIOS INDIANA 12 LOST LANGUAGES ESTUDIOS INDIANA OF THE PERUVIAN NORTH COAST COAST NORTH PERUVIAN THE OF This book is about the original indigenous languages of the Peruvian North Coast, likely associated with the important pre-Columbian societies of the coastal deserts, but poorly documented and now irrevocably lost Sechura and Tallán in Piura, Mochica in Lambayeque and La Libertad, and further south Quingnam, perhaps spoken as far south as the Central Coast. The book presents the original distribution of these languages in early colonial Matthias Urban times, discusses available and lost sources, and traces their demise as speakers switched to Spanish at different points of time after conquest. To the extent possible, the book also explores what can be learned about the sound system, grammar, and lexicon of the North Coast languages from the available materials. It explores what can be said on past language contacts and the linguistic areality of the North Coast and Northern Peru as a whole, and asks to what extent linguistic boundaries on the North Coast can be projected into the pre-Columbian past. ESTUDIOS INDIANA ISBN 978-3-7861-2826-7 12 Ibero-Amerikanisches Institut Preußischer Kulturbesitz | Gebr. Mann Verlag • Berlin Matthias Urban Lost Languages of the Peruvian North Coast ESTUDIOS INDIANA 12 Lost Languages of the Peruvian North Coast Matthias Urban Gebr. Mann Verlag • Berlin 2019 Estudios Indiana The monographs and essay collections in the Estudios Indiana series present the results of research on multiethnic, indigenous, and Afro-American societies and cultures in Latin America, both contemporary and historical. -

Boston Don't Look Back Album Download Party - Boston - Dont Look Back (CD, Album) Download Full Album Zip Cd Mp3 Vinyl Flac
boston don't look back album download Party - Boston - Dont Look Back (CD, Album) download full album zip cd mp3 vinyl flac. Label: Epic - CDKNIC • Format: CD Album, Reissue • Country: South Africa • Genre: Rock • Style: Hard Rock, Classic Rock Boston - Don't Look Back (CD) | Discogs Explore5/5(1). View credits, reviews, tracks and shop for the CD release of Don't Look Back on Discogs. Label: Epic - EK • Format: CD Album, Reissue • Country: US • Genre: Rock • Style: Pop Rock, Classic Rock4/5(7). 4 hours ago · Label: Epic - ESCA • Series: Epic Nice Price Line • Format: CD Album, Reissue • Country: Japan • Genre: Rock • Style: Arena Rock Boston - Don't Look Back = ドント・ルック・バック (, CD) | Discogs/5(2). Hal Leonard. New West. Maximum Guitar. Retrieved October 10, October 14, Official Charts Company. Album) Hits. Namespaces Article Talk. Views Read Edit View history. Help Community portal Recent changes Upload file. Download as PDF Printable version. Hard rockarena rockprogressive rock, Album) . Boston Don't Look Back Party - Boston - Dont Look Back (CD Third Stage Christgau's Record Guide. B— [2]. US Billboard [23]. Canada RPM Albums [24]. Norway VG-lista [26]. Expectations were running exceedingly high, but Scholz rose to the challenge without allowing the pressure to affect his acute work ethic. Ironically, the party was over for another eight years. When the group finally reconvened for Third Stagethe sound was faintly reminiscent, but aside from Scholz and singer Brad Delp, the other players had come and gone. Occasional resurfacings have yet to reveal any major improvements to the grand invasion of the late 70s. -

Clouds Lyrics - NF
Clouds Lyrics - NF Clouds is a song by NF . CLOUDS is the third single off of NF's mixtape "CLOUDS". Clouds Lyrics Clouds Calmly feel myself evolving Appalling, so much I'm not divulging Been stalling, I think I hear applauding, they're calling Mixtapes aren't my thing, but it's been awfully exhausting Hanging onto songs this long is daunting (Yeah) Which caused me to have to make a call I thought was ballsy Resulting in what you see today, proceed indulging As always, the one-trick pony's here, so quit your sulking Born efficient, got ambition, sorta vicious, yup, that's me Not artistic, unrealistic, chauvinistic, not those things Go the distance, so prolific, posts are cryptic, move swiftly Unsubmissive, the king of mischief The golden ticket, rare sight to see I stay committed, embrace the rigid I'm playful with it, yeah, basically www.lyricssymphony.com Too great to mimic, you hate, you're bitter No favoritism, that's fine with me Create the riddles, portrayed uncivil Unsafe a little, oh, yes, indeed It's plain and simple, I'm far from brittle Unbreakable, you following? I'm Bruce Willis in a train wreck I'm like trading in your car for a new jack I'm like having a boss getting upset 'Cause you asked him for less on your paycheck I'm like doing headstands with a broke neck I'm like watching your kid take his first steps I'm like saying Bill Gates couldn't pay rent 'Cause he's too broke, where am I going with this? Unbelievable, yes, yes, inconceivable See myself as fairly reasonable But at times I can be stubborn, so If I have to -
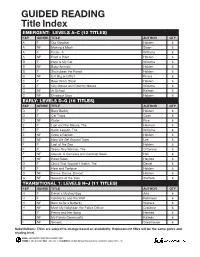
GUIDED READING Title Index
GUIDED READING Title Index EMERGENT: LEVELS A–C (12 TITLES) F&P GENRE TITLE AUTHOR QTY A F Our Weather Holden 6 A NF Making a Mask Sloan 6 A F Picnic, A Williams 6 A NF Plant a Plant Holden 6 B F Here Is My Cat Williams 6 B NF Baby Animals Holden 6 B F Stickybeak the Parrot Holden 6 B NF Is It Big or Little? Rivera 6 C F Blow Wind, Blow! Holden 6 C F City Mouse and Country Mouse Williams 6 C NF At School Kalman 6 C NF Dinosaur Days Holden 6 EARLY: LEVELS D–G (15 TITLES) F&P GENRE TITLE AUTHOR QTY D F Busy Buddy Holden 6 D F Cat Traps Coxe 6 D NF Water Rice 6 E F Lion and the Mouse, The Herman 6 E F Swim Lesson, The Williams 6 E NF Grow a Garden Holden 6 E NF How We Get Around Town Lee 6 F F Lost at the Zoo Holden 6 F F Teeny Tiny Woman, The O'Connor 6 F NF Clouds: A Compare and Contrast Book Hall 6 F NF Road Rules Hayhoe 6 G F Chick That Wouldn’t Hatch, The Daniel 6 G F Hare and Tortoise Holden 6 G NF Dance, Dance, Dance! Holden 6 G NF Seasons of the Year Steffora 6 TRANSITIONAL 1: LEVELS H–J (11 TITLES) F&P GENRE TITLE AUTHOR QTY H F Daniel's Mystery Egg Ada 6 H F Goldilocks and the Wolf Robinson 6 H NF Born to Be a Butterfly Wallace 6 H NF Meet My Neighbor, the Police Officer Crabtree 6 I F Penny and Her Song Henkes 6 I NF My Family Community Kalman 6 I NF Senses Greathouse 6 Substitutions: Titles are subject to change based on availability. -

Nf Perception How to Download Digital Album HQ :- NF Clouds (The Mixtape) Full Album Download
nf perception how to download digital album HQ :- NF Clouds (The Mixtape) Full ALbum Download. HQ :- NF Clouds (The Mixtape) Full ALbum Download Today, the myth-making, chart-topping Michigan rapper NF announces his latest project and first mixtape, CLOUDS (THE MIXTAPE) out March 26, 2021, which is now available for pre-order/pre-add via NF Real Music/Caroline here. NF has also released the ominous, chest-beating title track, “CLOUDS,” in tandem with a fittingly cinematic video. Listen here and watch here. With “CLOUDS,” NF outlines his reasons for releasing this mixtape now. “Hanging onto songs this long is daunting,” he raps, matter-of-factly. He then playfully delivers clever lines in unison with a sparse violin melody before his delivery becomes more fiery, matching a thundering, industrial beat. Throughout, the technically gifted MC passionately strings together intricate rhymes about his continued ascent and the gravity of his ambitions: “It’s probable / That I might press the envelope / Ideas so astronomical / Sometimes I find them comical.” “CLOUDS” follows NF’s last surprise single, October 2020’s “CHASING_(DEMO),” which featured 15-year-old Australian fan Mikayla Sippel. A gripping ballad about breaking down and wanting to escape the world, “CHASING (DEMO)” arrived just as calls for new music from NF’s fervent fanbase were becoming deafening. Ever since his Billboard-topping fourth album, 2019’s The Search, fans have eagerly awaited more of his emotive and brutally honest songwriting, grand production, and sharp delivery. This new single suggests that CLOUDS (THE MIXTAPE) will be well worth the wait.