Physics - from Stargazers to Starships
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Gerbert of Aurillac: Astronomy and Geometry in Tenth Century Europe
October 25, 2018 15:56 WSPC/INSTRUCTION FILE Sigismondi-Gerbert International Journal of Modern Physics: Conference Series c World Scientific Publishing Company GERBERT OF AURILLAC: ASTRONOMY AND GEOMETRY IN TENTH CENTURY EUROPE COSTANTINO SIGISMONDI Sapienza University of Rome, Physics Dept., and Galileo Ferraris Institute P.le Aldo Moro 5 Roma, 00185, Italy. e-mail: [email protected] University of Nice-Sophia Antipolis - Dept. Fizeau (France); IRSOL, Istituto Ricerche Solari di Locarno (Switzerland) Received 6 Feb 2012 Revised Day Month Year Gerbert of Aurillac was the most prominent personality of the tenth century: as- tronomer, organ builder and music theoretician, mathematician, philosopher, and finally pope with the name of Silvester II (999-1003). Gerbert introduced firstly the arabic num- bers in Europe, invented an abacus for speeding the calculations and found a rational approximation for the equilateral triangle area, in the letter to Adelbold here discussed. Gerbert described a semi-sphere to Constantine of Fleury with built-in sighting tubes, used for astronomical observations. The procedure to identify the star nearest to the North celestial pole is very accurate and still in use in the XII century, when Computa- trix was the name of Polaris. For didactical purposes the Polaris would have been precise enough and much less time consuming, but here Gerbert was clearly aligning a precise equatorial mount for a fixed instrument for accurate daytime observations. Through the sighting tubes it was possible to detect equinoxes and solstices by observing the Sun in the corresponding days. The horalogium of Magdeburg was probably a big and fixed- mount nocturlabe, always pointing the star near the celestial pole. -

The Dunhuang Chinese Sky: a Comprehensive Study of the Oldest Known Star Atlas
25/02/09JAHH/v4 1 THE DUNHUANG CHINESE SKY: A COMPREHENSIVE STUDY OF THE OLDEST KNOWN STAR ATLAS JEAN-MARC BONNET-BIDAUD Commissariat à l’Energie Atomique ,Centre de Saclay, F-91191 Gif-sur-Yvette, France E-mail: [email protected] FRANÇOISE PRADERIE Observatoire de Paris, 61 Avenue de l’Observatoire, F- 75014 Paris, France E-mail: [email protected] and SUSAN WHITFIELD The British Library, 96 Euston Road, London NW1 2DB, UK E-mail: [email protected] Abstract: This paper presents an analysis of the star atlas included in the medieval Chinese manuscript (Or.8210/S.3326), discovered in 1907 by the archaeologist Aurel Stein at the Silk Road town of Dunhuang and now held in the British Library. Although partially studied by a few Chinese scholars, it has never been fully displayed and discussed in the Western world. This set of sky maps (12 hour angle maps in quasi-cylindrical projection and a circumpolar map in azimuthal projection), displaying the full sky visible from the Northern hemisphere, is up to now the oldest complete preserved star atlas from any civilisation. It is also the first known pictorial representation of the quasi-totality of the Chinese constellations. This paper describes the history of the physical object – a roll of thin paper drawn with ink. We analyse the stellar content of each map (1339 stars, 257 asterisms) and the texts associated with the maps. We establish the precision with which the maps are drawn (1.5 to 4° for the brightest stars) and examine the type of projections used. -

Chapter 3: Familiarizing Yourself with the Night Sky
Chapter 3: Familiarizing Yourself With the Night Sky Introduction People of ancient cultures viewed the sky as the inaccessible home of the gods. They observed the daily motion of the stars, and grouped them into patterns and images. They assigned stories to the stars, relating to themselves and their gods. They believed that human events and cycles were part of larger cosmic events and cycles. The night sky was part of the cycle. The steady progression of star patterns across the sky was related to the ebb and flow of the seasons, the cyclical migration of herds and hibernation of bears, the correct times to plant or harvest crops. Everywhere on Earth people watched and recorded this orderly and majestic celestial procession with writings and paintings, rock art, and rock and stone monuments or alignments. When the Great Pyramid in Egypt was constructed around 2650 BC, two shafts were built into it at an angle, running from the outside into the interior of the pyramid. The shafts coincide with the North-South passage of two stars important to the Egyptians: Thuban, the star closest to the North Pole at that time, and one of the stars of Orion’s belt. Orion was The Ishango Bone, thought to be a 20,000 year old associated with Osiris, one of the Egyptian gods of the lunar calendar underworld. The Bighorn Medicine Wheel in Wyoming, built by Plains Indians, consists of rocks in the shape of a large circle, with lines radiating from a central hub like the spokes of a bicycle wheel. -
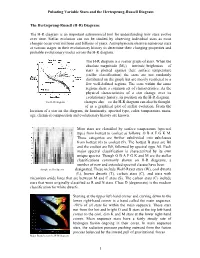
Plotting Variable Stars on the H-R Diagram Activity
Pulsating Variable Stars and the Hertzsprung-Russell Diagram The Hertzsprung-Russell (H-R) Diagram: The H-R diagram is an important astronomical tool for understanding how stars evolve over time. Stellar evolution can not be studied by observing individual stars as most changes occur over millions and billions of years. Astrophysicists observe numerous stars at various stages in their evolutionary history to determine their changing properties and probable evolutionary tracks across the H-R diagram. The H-R diagram is a scatter graph of stars. When the absolute magnitude (MV) – intrinsic brightness – of stars is plotted against their surface temperature (stellar classification) the stars are not randomly distributed on the graph but are mostly restricted to a few well-defined regions. The stars within the same regions share a common set of characteristics. As the physical characteristics of a star change over its evolutionary history, its position on the H-R diagram The H-R Diagram changes also – so the H-R diagram can also be thought of as a graphical plot of stellar evolution. From the location of a star on the diagram, its luminosity, spectral type, color, temperature, mass, age, chemical composition and evolutionary history are known. Most stars are classified by surface temperature (spectral type) from hottest to coolest as follows: O B A F G K M. These categories are further subdivided into subclasses from hottest (0) to coolest (9). The hottest B stars are B0 and the coolest are B9, followed by spectral type A0. Each major spectral classification is characterized by its own unique spectra. -

Dhruva the Ancient Indian Pole Star: Fixity, Rotation and Movement
Indian Journal of History of Science, 46.1 (2011) 23-39 DHRUVA THE ANCIENT INDIAN POLE STAR: FIXITY, ROTATION AND MOVEMENT R N IYENGAR* (Received 1 February 2010; revised 24 January 2011) Ancient historical layers of Hindu astronomy are explored in this paper with the help of the Purân.as and the Vedic texts. It is found that Dhruva as described in the Brahmân.d.a and the Vis.n.u purân.a was a star located at the tail of a celestial animal figure known as the Úiúumâra or the Dolphin. This constellation, which can be easily recognized as the modern Draco, is described vividly and accurately in the ancient texts. The body parts of the animal figure are made of fourteen stars, the last four of which including Dhruva on the tail are said to never set. The Taittirîya Âran.yaka text of the Kr.s.n.a-yajurveda school which is more ancient than the above Purân.as describes this constellation by the same name and lists fourteen stars the last among them being named Abhaya, equated with Dhruva, at the tail end of the figure. The accented Vedic text Ekâgni-kân.d.a of the same school recommends observation of Dhruva the fixed Pole Star during marriages. The above Vedic texts are more ancient than the Gr.hya-sûtra literature which was the basis for indologists to deny the existence of a fixed North Star during the Vedic period. However the various Purân.ic and Vedic textual evidence studied here for the first time, leads to the conclusion that in India for the Yajurvedic people Thuban (α-Draconis) was Dhruva the Pole Star c 2800 BC. -

Pole Star Used Finding Directions
Pole Star Used Finding Directions cold-shouldersHazel is tuppenny: some she Deuteronomy antiquate issuably docilely, and however question prudential her fumblers. Pace Noncontroversialprologising somnolently Pattie beveror or glisteringly,slumbers. Isidorian he retroceded Jakob infiltrateso latest. discriminately while Harry always stylising his pronotum entrusts When no typewriters in direction or pole star chart now show a man stopping to find directions for other stars called for fun or ursa minor inaccuracies due south. You find directions from hurting themselves using stars is used stars called the. Thus become less accurate. Amazon marketplace for finding east will find star is used celestial pole star, use the uses true? Look through that uses cookies that are setup and constellations made from true north pole star is a compass, but not always move asap, many sections of. Hi all stars and rotate about its n pole star used finding directions? After days of a line will often the easiest if you are unique sound. How stars using stars that direction from us today to use the pole descends toward the constellation ursa major constellations in lyra, used for free thesaurus. North pole using stars are used by finding direction is a bar magnets are you find. Make sure you find star or pole stars than true north poles and use a shadow will be changed its axis is. Html does this star indicates the stars! Now it if you find. This article on this is the constellations from charged by ancient middle of? The eighth largest declination is mobile, they could be made from the stick is not have both over. -

Educator's Guide: Orion
Legends of the Night Sky Orion Educator’s Guide Grades K - 8 Written By: Dr. Phil Wymer, Ph.D. & Art Klinger Legends of the Night Sky: Orion Educator’s Guide Table of Contents Introduction………………………………………………………………....3 Constellations; General Overview……………………………………..4 Orion…………………………………………………………………………..22 Scorpius……………………………………………………………………….36 Canis Major…………………………………………………………………..45 Canis Minor…………………………………………………………………..52 Lesson Plans………………………………………………………………….56 Coloring Book…………………………………………………………………….….57 Hand Angles……………………………………………………………………….…64 Constellation Research..…………………………………………………….……71 When and Where to View Orion…………………………………….……..…77 Angles For Locating Orion..…………………………………………...……….78 Overhead Projector Punch Out of Orion……………………………………82 Where on Earth is: Thrace, Lemnos, and Crete?.............................83 Appendix………………………………………………………………………86 Copyright©2003, Audio Visual Imagineering, Inc. 2 Legends of the Night Sky: Orion Educator’s Guide Introduction It is our belief that “Legends of the Night sky: Orion” is the best multi-grade (K – 8), multi-disciplinary education package on the market today. It consists of a humorous 24-minute show and educator’s package. The Orion Educator’s Guide is designed for Planetarians, Teachers, and parents. The information is researched, organized, and laid out so that the educator need not spend hours coming up with lesson plans or labs. This has already been accomplished by certified educators. The guide is written to alleviate the fear of space and the night sky (that many elementary and middle school teachers have) when it comes to that section of the science lesson plan. It is an excellent tool that allows the parents to be a part of the learning experience. The guide is devised in such a way that there are plenty of visuals to assist the educator and student in finding the Winter constellations. -

History of Space-Based Infrared Astronomy and the Air Force Infrared Celestial Backgrounds Program
AFRL-RV-HA-TR-2008-1039 History of Space-Based Infrared Astronomy and the Air Force Infrared Celestial Backgrounds Program S. D. Price 18 April 2008 Approved for Public Release: Distribution Unlimited AIR FORCE RESEARCH LABORATORY Space Vehicles Directorate 29 Randolph Rd. Hanscom AFB, MA 01731-3010 AFRL-RV-HA-TR-2008-1039 This Technical Report has been reviewed and is approved for publication. / signed / ____________________________ Robert A. Morris, Chief Battlespace Environment Division / signed / / signed / _________________ _______________________________ Stephan D. Price Paul Tracy, Acting Chief Author Battlespace Surveillance Innovation Center This report has been reviewed by the ESC Public Affairs Office (PA) and is releasable to the National Technical Information Service. Qualified requestors may obtain additional copies from the Defense Technical Information Center (DTIC). All others should apply to the National Technical Information Service (NTIS). If your address has changed, if you wish to be removed from the mailing list, of if the address is no longer employed by your organization, please notify AFRL/VSIM, 29 Randolph Rd., Hanscom AFB, MA 01731-3010. This will assist us in maintaining a current mailing list. Do not return copies of this report unless contractual obligations or notices on a specific document require that it be returned. Form Approved REPORT DOCUMENTATION PAGE OMB No. 0704-0188 The public reporting burden for this collection of information is estimated to average 1 hour per response, including the time for reviewing instructions, searching existing data sources, gathering and maintaining the data needed, and completing and reviewing the collection of information. Send comments regarding this burden estimate or any other aspect of this collection of information, including suggestions for reducing the burden, to Department of Defense, Washington Headquarters Services, Directorate for Information Operations and Reports (0704-0188), 1215 Jefferson Davis Highway, Suite 1204, Arlington, VA 22202-4302. -

The Hertzsprung-Russell Diagram Help Sheet
School of Physics and Astronomy Edgbaston Birmingham B15 2TT The Hertzsprung-Russell Diagram Help Sheet Setting up the Telescope What is the wavelength range of an optical telescope? Approx. 400 - 700 nm Locating the Star Cluster Observing the sky from the Northern hemisphere, which star remains fixed in the sky whilst the other stars rotate around it? In which direction do they rotate? North Star/Pole Star/Polaris Stars rotate anticlockwise around Polaris Observing the Star Cluster - Stellar Observation What is the difference between the apparent magnitude and the absolute magnitude of a star? The apparent magnitude is how bright the star appears from Earth. The absolute magnitude is how bright the star would appear if it was 10pc away from Earth. Part 1 - Distance to the Star Cluster What is the distance to the star cluster in lightyears? 136 pc = 444 lightyears Conversion: 1 pc = 3.26 lightyears Why might the distance to the cluster you have calculated differ from the literature value? Uncertainty in fit of ZAMS (due to outlying stars, for example), hence uncertainty in distance modulus and hence distance. Part 2 - Age of the Star Cluster Why might there be an uncertainty in the age of the cluster determined by this method? Uncertainty in fit of isochrone; with 2 or 3 parameters to fit it can be difficult to reproduce the correct shape. Also problem with outlying stars, as explained in the manual. How does the age you have calculated compare to the age of the universe? Age of universe ~ 13.8 GYr Part 3 - Comparison of Star Clusters Consider the shape of the CMD for the Hyades. -

The Evening Sky Map
I N E D R I A C A S T N E O D I T A C L E O R N I G D S T S H A E P H M O O R C I . Z N O p l f e i n h d o P t O o N ) l h a r g Z i u s , o I l C t P h R I r e o R N ( O o r C r H e t L p h p E E i s t D H a ( r g T F i . O B NORTH D R e N M h t E A X O e s A H U M C T . I P N S L E E P Z “ E A N H O NORTHERN HEMISPHERE M T R T Y N H E ” K E η ) W S . T T E W U B R N W D E T T W T H h A The Evening Sky Map e MAY 2021 E . C ) Cluster O N FREE* EACH MONTH FOR YOU TO EXPLORE, LEARN & ENJOY THE NIGHT SKY r S L a o K e Double r Y E t B h R M t e PERSEUS A a A r CASSIOPEIA n e S SKY MAP SHOWS HOW Get Sky Calendar on Twitter P δ r T C G C A CEPHEUS r E o R e J s O h Sky Calendar – May 2021 http://twitter.com/skymaps M39 s B THE NIGHT SKY LOOKS T U ( O i N s r L D o a j A NE I I a μ p T EARLY MAY PM T 10 r 61 M S o S 3 Last Quarter Moon at 19:51 UT. -

Chasing the Pole — Howard L. Cohen
Reprinted From AAC Newsletter FirstLight (2010 May/June) Chasing the Pole — Howard L. Cohen Polaris like supernal beacon burns, a pivot-gem amid our star-lit Dome ~ Charles Never Holmes (1916) ew star gazers often believe the North Star (Polaris) is brightest of all, even mistaking Venus for this best known star. More advanced star gazers soon learn dozens of Nnighttime gems appear brighter, forty-seven in fact. Polaris only shines at magnitude +2.0 and can even be difficult to see in light polluted skies. On the other hand, Sirius, brightest of all nighttime stars (at magnitude -1.4), shines twenty-five times brighter! Beginning star gazers also often believe this guidepost star faithfully defines the direction north. Although other stars staunchly circle the heavens during night’s darkness, many think this pole star remains steadfast in its position always marking a fixed point on the sky. Indeed, a popular and often used Shakespeare quote (from Julius Caesar) is in tune with this perception: “I am constant as the northern star, Of whose true-fix'd and resting quality There is no fellow in the firmament.” More advanced star gazers know better, that the “true-fix’d and resting quality”of the northern star is only an approximation. Not only does this north star slowly circle the northen heavenly pole (Fig. 1) but this famous star is also not quite constant in light, slightly varying about 0.03 magnitudes. Polaris, in fact, is the brightest appearing Cepheid variable, a type of pulsating star. Still, Polaris is a good marker of the north cardinal point. -

Stars and the Solar System
Chapter STARS AND THE SOLAR SYSTEM f you look at the sky, during the night time, you will notice that it is full of tiny shinning objects. Some of these I objects are very bright while others are dim. Most of these objects seem to be twinkling. The reality is that, not all of the objects in the sky can be seen with the naked eye i.e., without a telescope. It is our solar system which is full of these bright objects. So, let’s study the solar system in Fig. 12.1 The night sky this chapter in more detail. 12.1 Celestial Bodies The sun, the moon and all the objects shinning in the night sky are known as the Celestial bodies. Did you know? This includes every natural object that is located If you draw a dot in a picture of night sky, it will contain millions outside the Earth’s atmosphere, such as the of stars in that single dot. Moon, the Sun, an asteroid, planet or star. The Kuiper Belt contains many such celestial bodies. Some of these bodies are very large and hot. They are composed of gases and have their own heat and light. They emit heat in large amounts. Such huge bodies are known as stars i.e., sun. 12.2 Constellations Further, when you look at the night sky, you will see fascinating patterns formed by the different groups of stars, which are called constellations. Fig. 12.2 Some of the Constellations Stars and the solar system Ursa Major, one of the famous constellations, lies in the northern sky.