DOCSLIB.ORG

Unknotting Number and Knot Diagram 1 Introduction

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Unknotting Number and Knot Diagram 1 Introduction REVISTA MATEMÁTICA de la Universidad Complutense de Madrid Volumen 9, número 2: 1996 http://dx.doi.org/10.5209/rev_REMA.1996.v9.n2.17585 Unknotting number and knot diagram Yasutaka NAKANISHI Abstract TImis note is a continuation of [Nl], Wbere we have discusged tbe unknotting number of knots With rspect tía knot diagrams. Wc wilI show that for every minimum-crossing knot-diagram among ah unknotting-number-one two-bridge knot there exist crossings whose exchange yields tIme trivial knot, ib tbe tbird Tait conjecture is true. 1 Introduction The unknotting rtumber uQc) is defined tobe the minimum number of ex- changes of over- and under- crossing required to convertk into the trivial knot over all knot díagrams representing 1v. The unknotting number is intuitive and attractive for knot theorists and there is no algorithm to compute it for a given knot until noW. Qur motivation is to fixid 811 ap- proach. For a gíven knot, there are finíte number of minimum crossíng knot diagrams. If tIme condition “all knot diagrams” is restricted to “al! minimum crossing knot diagrams”, then We cannot obtain tIme unknot- ting nmnbers as in [Nl] and [B}: The minirnum crossing diagram of the knot lOs as lxi Fig. 1(a) (or 514 in the Conway notation [C]) is unique up to homeomorphísm of projected 2-sphere, where excImanges of tWO crossings never yield the trivial knot, however the unknotting number of 108 is tWo. (There is another diagram of the knot lOs Where exehanges 1991 Maihematice Subject Classlfication. 57M25. Servido Publicaciones Univ. Complutense. Madrid, 1996. 360 Yasutaka Nakanishi of two erossings yield the trivial knot). The author is afraid that this sítuation is not exceptional. He has raigal a question: Let K be a mrnimum crossing knot diagram of a knot 1v. Can we conved K into K’ With u(k’) .c u(1v) by exehange of a croising? II the auswer is affirmative for alí knots, we can give an algorithm. For tIme diagram as in Fig. 1 (a), we can conved the knot lOs into 62 wíth u(62) = 1 by exchange of the croissing mariced by the asterisk. (a) (b) (c) Fig. 1 In the aboye, it is necessary that K is a minimum cróssing diagram: Fig. 1 (b) and (c) illustrate tWo diagram of the famous ConWay 11 crossing lcnot. The central diagram (b) has the mínimum number of crossings, and exchange of the crossing marked by tIme asterisk yields the trivial knot. TIme right one (c) is not a mnumum crossing diagram, and there is no crossing Whose exchange yields the trivial knot. In fact, it is seen iii [N2] that, for any unknotting-number-one knot, there exist a diagram where is no crossing whose exchange yields the trivial knot. In tImis note, We give an affirmative answer for tIme class of unknotting- number-one tWo-bridge knots. Kanenobu aud Murakami [KM] char- acterized the unlcnotting-nuxnber-one tWo-bridge knots as knots repre- sented iii tIme Conway notation by C(a, ~1•~2< , a,,, ±2<a,,~, a~, —al). Unknotting number ¡md ... 361 In section 2, ~e deform the diagram aboye into the alternating one While keeping the crossing Whose exchange yields tlie trivial lcnot. Since a reduced alternating diagram mnst have the minimum number of cross- ings, by Kauffman, Murasugi [Ml and ThistlethWaite [Th], We have the followíng. TImeorem A. For a certain minimum crossing diagram of art unknotting- number-one tino-bridge krtot, titere extit crossing tu/tose exehange yields ihe trivial knot. By the third Tait conjecture, all knot diagrams with the mínimum crossings are transformed by a finite sequence of flypes. Here, a croissing whose exchange yields the trivial knot survives after fiyping. Hence, We have the required result: Theorem B. For evertj minimum crossing diagram of any givert unknotting-number-one tino-bridge knot, there extit crossirtgs in/tíase ex- chartge yields tite trivial krtot, up tía tite third Tait conjecture (i.e. if ¡¿ti conjecture turus Lo be true). 2. Deformation and Proof Proposition 1([KMJ). Tite unknottirtg-number-one tino-bridge ¡moLa can be represented in tite Oortway notation by C(a, a 1, ~2, - ,a,, +2, By the proposition aboye, an unknotting-number-one tWo-bridge knot can be illustrated as in Fig. 2. Here, a, a2, G4,~• mean nunibers of right-half-twist and a1, a~, - - mean numbers of left-half-tWist. The Fig. 2 shows the case « = 3, aj = 2, a2 3,.... And a single exchange at each crossing marked by an asterisk yields tIme trivial lcnot. ... ••. ./ZY$42i~jj¿~jjjjj11 NI» a a1 (12 a,. 2 —a,. —a2 —(Ii Fig. 2 In this section, We deform the diagram aboye into an alternating díagram. 362 Yasu talca Nakanishi In tite first step, We deform a diagram so that every pair of integers a 1, a1+i(1 =i =rt —1) has the same signas in Fig. 3. We rotate by ir the central part of three strings from the second crossing corresponding ta ~ through the second last crossing corresponding to —a¿~’ and tIme number of crossíngs is decreased by two with preser-ving a tWo-bridge form aud the crossings mariced by the asterisks. -½~IL~ a, ~ —a~+~ —a~ Fig. 3 Since the nunher of crossings is finite, a diagram can be deformed so that every pair of integers aj, a¿+i(1 =1 n — 1) has the same sign by a finite sequence of operations in tite first step. In tlie second step, we deform a diagram hito an alternating diagram with preservíng the crossings marked by the asterisks. There are at most twa possibilities of non-alternating after the flrst step; tite pair of a and Unknotting number and ... 363 a¡, and eíther one of the pair of a,, and +2 or tIme pair of +2 aud —a,.. t~- —4 a a1 Fig. 4 Por the former case, We push out the subarc from tIme last crossing cor- responding to a through tIme flrst crossing corresponding to a1 as in Fig. 4. Por tIme latter case, we pusIm out tIme subarc from tIme last crossing corresponding to a,. through the first crossing corresponding to +2 (or tIme subarc from tIme last crossing corresponding to +2 thraugh the first 364 Yasutalca Nakanishi crossing corresponding to -a,.) as in Fig. 5. —4 a~ —2 u— 2 —a, —>1 Fig. 5 TIme diagram after the second step is an alternating diagram and it is already reduced. By the folloWing result by Kauffman, Murasugi [M] and ThistlethWaite [Th], it is a minimum crossing diagram and it has at least <me crossing Whose exchange yield the trivial knot. Proposition 2 (The second lMit conjecture [M], [Th]). Tino (con- nected and proper) alternating diagrame of art alternaLíng knot ¡¿ave tite samA number of crossings. Unknotting number and ... 365 A flype is defined to be an operation on knot diagram as lxi Fig. 6. Here We remariced that the resulta of exchanges of the crosaings mariced by the asterisks have the sanie knot type. So we can say a crossing whose exchange yields the trivial knot survives after flyping. IIn-m Fig. 6 FolloWing the third TaU conjecture [T], all reduced alternating dia- grams of the sanie bat type can be deformed into eacIm other by a finite sequence of flypes. Hence, there exist crossíngs Whose exchange yields the trivial knot on every mínimum crossing diagram of an unknotting- number-one tWo-bridge knot. Acknawledgement. The author Would like to expresa his gratítude to Professor 3. M. Montesinos for his suggestions and showing English correction. References ¡II] 8. A. Bleiler, A note mi unknotting number, Math. Proc. Cambrídge Phils. Soc. 96 (1984), 469-471. [C] 3. H. ConWay, An enumeratior¿ of knoL and lira/es, ami titeir algebraic properties, Computational problem in Abstract Algebra (Oxford 1967), Pergamon Press, 1970, Pp. 329-358. [KM] T. Kanenobu and H. Murakami, Tino-bridge knots initit unknotting number one, Proc. Amer. Math. Soc 98 (1986), 499-502. 366 Yasutaka Nakanishi [MJ K. Murasugí, iones potynomials arad clasaical conjectures ira IctioL theory, Topology 26 (1987), 187-194. [Nl] Y. Nakanishi, UrtknotLirzg numbers and krtot diagrams with tite imum crossirags, Math. Seminar Notes Kobe Univ. 11 (1983), 257- 258. 1N21 Y. Naicanishí, Union arad Langle, to appear in Proc. Amer. Math. Soc. IT] P. G. Tait, Ort knots, Scientific paper 1, Cambridge Univ. Press, London, 1989, pp. 273-347. [Th] M. B. Thistlethwaíte, A spanraing tree expansion of Lhe iones poly- rwmial, Topology 26 (1987), 297-309. Department of Mathematics Recibido: 16 de Marzo de 1995 Kobe University Nada-ku, Kobe, 657 Japan E-mail addres: nakanisiamath.s.kobe-u.ac.jp.
Load more

Recommended publications
  • Conservation of Complex Knotting and Slipknotting Patterns in Proteins
    Conservation of complex knotting and PNAS PLUS slipknotting patterns in proteins Joanna I. Sułkowskaa,1,2, Eric J. Rawdonb,1, Kenneth C. Millettc, Jose N. Onuchicd,2, and Andrzej Stasiake aCenter for Theoretical Biological Physics, University of California at San Diego, La Jolla, CA 92037; bDepartment of Mathematics, University of St. Thomas, Saint Paul, MN 55105; cDepartment of Mathematics, University of California, Santa Barbara, CA 93106; dCenter for Theoretical Biological Physics , Rice University, Houston, TX 77005; and eCenter for Integrative Genomics, Faculty of Biology and Medicine, University of Lausanne, 1015 Lausanne, Switzerland Edited by* Michael S. Waterman, University of Southern California, Los Angeles, CA, and approved May 4, 2012 (received for review April 17, 2012) While analyzing all available protein structures for the presence of ers fixed configurations, in this case proteins in their native folded knots and slipknots, we detected a strict conservation of complex structures. Then they may be treated as frozen and thus unable to knotting patterns within and between several protein families undergo any deformation. despite their large sequence divergence. Because protein folding Several papers have described various interesting closure pathways leading to knotted native protein structures are slower procedures to capture the knot type of the native structure of and less efficient than those leading to unknotted proteins with a protein or a subchain of a closed chain (1, 3, 29–33). In general, similar size and sequence, the strict conservation of the knotting the strategy is to ensure that the closure procedure does not affect patterns indicates an important physiological role of knots and slip- the inherent entanglement in the analyzed protein chain or sub- knots in these proteins.
    [Show full text]
  • A Knot-Vice's Guide to Untangling Knot Theory, Undergraduate
    A Knot-vice’s Guide to Untangling Knot Theory Rebecca Hardenbrook Department of Mathematics University of Utah Rebecca Hardenbrook A Knot-vice’s Guide to Untangling Knot Theory 1 / 26 What is Not a Knot? Rebecca Hardenbrook A Knot-vice’s Guide to Untangling Knot Theory 2 / 26 What is a Knot? 2 A knot is an embedding of the circle in the Euclidean plane (R ). 3 Also defined as a closed, non-self-intersecting curve in R . 2 Represented by knot projections in R . Rebecca Hardenbrook A Knot-vice’s Guide to Untangling Knot Theory 3 / 26 Why Knots? Late nineteenth century chemists and physicists believed that a substance known as aether existed throughout all of space. Could knots represent the elements? Rebecca Hardenbrook A Knot-vice’s Guide to Untangling Knot Theory 4 / 26 Why Knots? Rebecca Hardenbrook A Knot-vice’s Guide to Untangling Knot Theory 5 / 26 Why Knots? Unfortunately, no. Nevertheless, mathematicians continued to study knots! Rebecca Hardenbrook A Knot-vice’s Guide to Untangling Knot Theory 6 / 26 Current Applications Natural knotting in DNA molecules (1980s). Credit: K. Kimura et al. (1999) Rebecca Hardenbrook A Knot-vice’s Guide to Untangling Knot Theory 7 / 26 Current Applications Chemical synthesis of knotted molecules – Dietrich-Buchecker and Sauvage (1988). Credit: J. Guo et al. (2010) Rebecca Hardenbrook A Knot-vice’s Guide to Untangling Knot Theory 8 / 26 Current Applications Use of lattice models, e.g. the Ising model (1925), and planar projection of knots to find a knot invariant via statistical mechanics. Credit: D. Chicherin, V.P.
    [Show full text]
  • CROSSING CHANGES and MINIMAL DIAGRAMS the Unknotting
    CROSSING CHANGES AND MINIMAL DIAGRAMS ISABEL K. DARCY The unknotting number of a knot is the minimal number of crossing changes needed to convert the knot into the unknot where the minimum is taken over all possible diagrams of the knot. For example, the minimal diagram of the knot 108 requires 3 crossing changes in order to change it to the unknot. Thus, by looking only at the minimal diagram of 108, it is clear that u(108) ≤ 3 (figure 1). Nakanishi [5] and Bleiler [2] proved that u(108) = 2. They found a non-minimal diagram of the knot 108 in which two crossing changes suffice to obtain the unknot (figure 2). Lower bounds on unknotting number can be found by looking at how knot invariants are affected by crossing changes. Nakanishi [5] and Bleiler [2] used signature to prove that u(108)=2. Figure 1. Minimal dia- Figure 2. A non-minimal dia- gram of knot 108 gram of knot 108 Bernhard [1] noticed that one can determine that u(108) = 2 by using a sequence of crossing changes within minimal diagrams and ambient isotopies as shown in figure. A crossing change within the minimal diagram of 108 results in the knot 62. We then use an ambient isotopy to change this non-minimal diagram of 62 to a minimal diagram. The unknot can then be obtained by changing one crossing within the minimal diagram of 62. Bernhard hypothesized that the unknotting number of a knot could be determined by only looking at minimal diagrams by using ambient isotopies between crossing changes.
    [Show full text]
  • Results on Nonorientable Surfaces for Knots and 2-Knots
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Dissertations, Theses, and Student Research Papers in Mathematics Mathematics, Department of 8-2021 Results on Nonorientable Surfaces for Knots and 2-knots Vincent Longo University of Nebraska-Lincoln, [email protected] Follow this and additional works at: https://digitalcommons.unl.edu/mathstudent Part of the Geometry and Topology Commons Longo, Vincent, "Results on Nonorientable Surfaces for Knots and 2-knots" (2021). Dissertations, Theses, and Student Research Papers in Mathematics. 111. https://digitalcommons.unl.edu/mathstudent/111 This Article is brought to you for free and open access by the Mathematics, Department of at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in Dissertations, Theses, and Student Research Papers in Mathematics by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. RESULTS ON NONORIENTABLE SURFACES FOR KNOTS AND 2-KNOTS by Vincent Longo A DISSERTATION Presented to the Faculty of The Graduate College at the University of Nebraska In Partial Fulfillment of Requirements For the Degree of Doctor of Philosophy Major: Mathematics Under the Supervision of Professors Alex Zupan and Mark Brittenham Lincoln, Nebraska May, 2021 RESULTS ON NONORIENTABLE SURFACES FOR KNOTS AND 2-KNOTS Vincent Longo, Ph.D. University of Nebraska, 2021 Advisor: Alex Zupan and Mark Brittenham A classical knot is a smooth embedding of the circle S1 into the 3-sphere S3. We can also consider embeddings of arbitrary surfaces (possibly nonorientable) into a 4-manifold, called knotted surfaces. In this thesis, we give an introduction to some of the basics of the studies of classical knots and knotted surfaces, then present some results about nonorientable surfaces bounded by classical knots and embeddings of nonorientable knotted surfaces.
    [Show full text]
  • On L-Space Knots Obtained from Unknotting Arcs in Alternating Diagrams
    New York Journal of Mathematics New York J. Math. 25 (2019) 518{540. On L-space knots obtained from unknotting arcs in alternating diagrams Andrew Donald, Duncan McCoy and Faramarz Vafaee Abstract. Let D be a diagram of an alternating knot with unknotting number one. The branched double cover of S3 branched over D is an L-space obtained by half integral surgery on a knot KD. We denote the set of all such knots KD by D. We characterize when KD 2 D is a torus knot, a satellite knot or a hyperbolic knot. In a different direction, we show that for a given n > 0, there are only finitely many L-space knots in D with genus less than n. Contents 1. Introduction 518 2. Almost alternating diagrams of the unknot 521 2.1. The corresponding operations in D 522 3. The geometry of knots in D 525 3.1. Torus knots in D 525 3.2. Constructing satellite knots in D 526 3.3. Substantial Conway spheres 534 References 538 1. Introduction A knot K ⊂ S3 is an L-space knot if it admits a positive Dehn surgery to an L-space.1 Examples include torus knots, and more broadly, Berge knots in S3 [Ber18]. In recent years, work by many researchers provided insight on the fiberedness [Ni07, Ghi08], positivity [Hed10], and various notions of simplicity of L-space knots [OS05b, Hed11, Krc18]. For more examples of L-space knots, see [Hom11, Hom16, HomLV14, Mot16, MotT14, Vaf15]. Received May 8, 2018. 2010 Mathematics Subject Classification. 57M25, 57M27.
    [Show full text]
  • The Conway Knot Is Not Slice
    THE CONWAY KNOT IS NOT SLICE LISA PICCIRILLO Abstract. A knot is said to be slice if it bounds a smooth properly embedded disk in B4. We demonstrate that the Conway knot, 11n34 in the Rolfsen tables, is not slice. This com- pletes the classification of slice knots under 13 crossings, and gives the first example of a non-slice knot which is both topologically slice and a positive mutant of a slice knot. 1. Introduction The classical study of knots in S3 is 3-dimensional; a knot is defined to be trivial if it bounds an embedded disk in S3. Concordance, first defined by Fox in [Fox62], is a 4-dimensional extension; a knot in S3 is trivial in concordance if it bounds an embedded disk in B4. In four dimensions one has to take care about what sort of disks are permitted. A knot is slice if it bounds a smoothly embedded disk in B4, and topologically slice if it bounds a locally flat disk in B4. There are many slice knots which are not the unknot, and many topologically slice knots which are not slice. It is natural to ask how characteristics of 3-dimensional knotting interact with concordance and questions of this sort are prevalent in the literature. Modifying a knot by positive mutation is particularly difficult to detect in concordance; we define positive mutation now. A Conway sphere for an oriented knot K is an embedded S2 in S3 that meets the knot 3 transversely in four points. The Conway sphere splits S into two 3-balls, B1 and B2, and ∗ K into two tangles KB1 and KB2 .
    [Show full text]
  • Transverse Unknotting Number and Family Trees
    Transverse Unknotting Number and Family Trees Blossom Jeong Senior Thesis in Mathematics Bryn Mawr College Lisa Traynor, Advisor May 8th, 2020 1 Abstract The unknotting number is a classical invariant for smooth knots, [1]. More recently, the concept of knot ancestry has been defined and explored, [3]. In my research, I explore how these concepts can be adapted to study trans- verse knots, which are smooth knots that satisfy an additional geometric condition imposed by a contact structure. 1. Introduction Smooth knots are well-studied objects in topology. A smooth knot is a closed curve in 3-dimensional space that does not intersect itself anywhere. Figure 1 shows a diagram of the unknot and a diagram of the positive trefoil knot. Figure 1. A diagram of the unknot and a diagram of the positive trefoil knot. Two knots are equivalent if one can be deformed to the other. It is well-known that two diagrams represent the same smooth knot if and only if their diagrams are equivalent through Reidemeister moves. On the other hand, to show that two knots are different, we need to construct an invariant that can distinguish them. For example, tricolorability shows that the trefoil is different from the unknot. Unknotting number is another invariant: it is known that every smooth knot diagram can be converted to the diagram of the unknot by changing crossings. This is used to define the smooth unknotting number, which measures the minimal number of times a knot must cross through itself in order to become the unknot. This thesis will focus on transverse knots, which are smooth knots that satisfy an ad- ditional geometric condition imposed by a contact structure.
    [Show full text]
  • An Index-Type Invariant of Knot Diagrams and Bounds for Unknotting Framed Knots
    An Index-Type Invariant of Knot Diagrams and Bounds for Unknotting Framed Knots Albert Yue Abstract We introduce a new knot diagram invariant called self-crossing in- dex, or SCI. We found that SCI changes by at most ±1 under framed Reidemeister moves, and specifically provides a lower bound for the num- ber of Ω3 moves. We also found that SCI is additive under connected sums, and is a Vassiliev invariant of order 1. We also conduct similar calculations with Hass and Nowik's diagram invariant and cowrithe, and present a relationship between forward/backward, ascending/descending, and positive/negative Ω3 moves. 1 Introduction A knot is an embedding of the circle in the three-dimensional space without self- intersection. Knot theory, the study of these knots, has applications in multiple fields. DNA often appears in the form of a ring, which can be further knotted into more complex knots. Furthermore, the enzyme topoisomerase facilitates a process in which a part of the DNA can temporarily break along the phos- phate backbone, physically change, and then be resealed [13], allowing for the regulation of DNA supercoiling, important in DNA replication for both grow- ing fork movement and in untangling chromosomes after replication [12]. Knot theory has also been used to determine whether a molecule is chiral or not [18]. In addition, knot theory has been found to have connections to mathematical models of statistic mechanics involving the partition function [13], as well as with quantum field theory [23] and string theory [14]. Knot diagrams are particularly of interest because we can construct and calculate knot invariants and thereby determine if knots are equivalent to each other.
    [Show full text]
  • A Bound on the Unknotting Number 1 Introduction
    Int. Journal of Math. Analysis, Vol. 3, 2009, no. 7, 339 - 345 A Bound on the Unknotting Number Madeti Prabhakar Department of Mathematics Indian Institute of Technology Guwahati Guwahati - 781 039, India [email protected] Abstract In this paper we give a bound on the unknotting number of a knot whose quasitoric braid representation is of type (3,q). Mathematics Subject Classification: 57M25 Keywords: Unknotting number, Quasitoric braids, Quasipositive knots 1 Introduction The unknotting number u(K) of a knot K is the minimum number of crossing changes required, taken over all knot diagrams representing K, to convert K into the trivial knot. It is easy to observe that u(K) ≥ 1 for any non-trivial K. However, finding u(K) for any arbitrary K is a very hard problem and in fact there are virtually no methods to determine u(K). By assuming the third Tait conjecture (all knot diagrams with the min- imum crossings are transformed by a finite sequences of flypes) to be true, Nakanishi [7] proved that for every minimum-crossing knot diagram among all unknotting-number-one two-bridge knot there exist crossings whose exchange yields the trivial knot. For a list of unknotting numbers of prime knots up to 10 crossings one can refer to [1]. Nakanishi [8] also gave an approach to de- termine the unknotting numbers of certain knots like 1083, 1097, 10105, 10106, 10109, 10117, 10121, 10139, 10152. For most of these knots Nakanishi determined the unknotting number by a surgical view of Alexander matrix. An important achievement was finding the unknotting number of any torus knot of type (p, q).
    [Show full text]
  • Knots of Genus One Or on the Number of Alternating Knots of Given Genus
    PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 129, Number 7, Pages 2141{2156 S 0002-9939(01)05823-3 Article electronically published on February 23, 2001 KNOTS OF GENUS ONE OR ON THE NUMBER OF ALTERNATING KNOTS OF GIVEN GENUS A. STOIMENOW (Communicated by Ronald A. Fintushel) Abstract. We prove that any non-hyperbolic genus one knot except the tre- foil does not have a minimal canonical Seifert surface and that there are only polynomially many in the crossing number positive knots of given genus or given unknotting number. 1. Introduction The motivation for the present paper came out of considerations of Gauß di- agrams recently introduced by Polyak and Viro [23] and Fiedler [12] and their applications to positive knots [29]. For the definition of a positive crossing, positive knot, Gauß diagram, linked pair p; q of crossings (denoted by p \ q)see[29]. Among others, the Polyak-Viro-Fiedler formulas gave a new elegant proof that any positive diagram of the unknot has only reducible crossings. A \classical" argument rewritten in terms of Gauß diagrams is as follows: Let D be such a diagram. Then the Seifert algorithm must give a disc on D (see [9, 29]). Hence n(D)=c(D)+1, where c(D) is the number of crossings of D and n(D)thenumber of its Seifert circles. Therefore, smoothing out each crossing in D must augment the number of components. If there were a linked pair in D (that is, a pair of crossings, such that smoothing them both out according to the usual skein rule, we obtain again a knot rather than a three component link diagram) we could choose it to be smoothed out at the beginning (since the result of smoothing out all crossings in D obviously is independent of the order of smoothings) and smoothing out the second crossing in the linked pair would reduce the number of components.
    [Show full text]
  • Unknotting Number of Some Knots
    Objective Preliminary Minimal Unknotting Crossing Data for Torus Knots Unknotting number of different knots Bibliography Unknotting Number of some knots Vikash Siwach (A joint work with Dr. M. Prabhakar) Department of Mathematics IIT Ropar, India October 29, 2013 1 / 37 Objective Preliminary Minimal Unknotting Crossing Data for Torus Knots Unknotting number of different knots Bibliography Outline 1 Objective 2 Preliminary 3 Minimal Unknotting Crossing Data for Torus Knots 4 Unknotting number of different knots 5 Bibliography 2 / 37 Objective Preliminary Minimal Unknotting Crossing Data for Torus Knots Unknotting number of different knots Bibliography Objective Here we find unknotting number of some knots by showing that each of them lie in an unknotting sequence of torus knot. First we find Minimal Unknotting Crossing Data (MUCD) for all torus knots and then by changing random sub-data from MUCD we indentify the resultant knot and its unknotting number. 3 / 37 Objective Preliminary Minimal Unknotting Crossing Data for Torus Knots Unknotting number of different knots Bibliography Preliminaries Unknotting Number: The unknotting number u(K) of a knot K is the minimum number of crossing changes required, taken over all knot diagrams representing K, to convert K into the trivial knot. Unknotting number for torus knot K(p, q) is (p − 1)(q − 1)/2.1 1P. Kronheimer and T. Mrowka, Gauge theory for embedded surfaces, I, Topology, 32 , 773-826. 1993. 4 / 37 Objective Preliminary Minimal Unknotting Crossing Data for Torus Knots Unknotting number of different knots Bibliography Preliminaries– Ascending and Descending diagram Ascending diagram(Descending diagram): Let K be a knot and D˜ be a based oriented knot diagram of K.
    [Show full text]
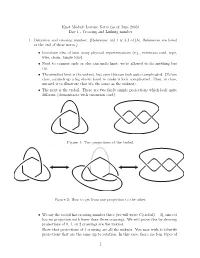
  • Knot Module Lecture Notes (As of June 2005) Day 1 - Crossing and Linking Number
    Knot Module Lecture Notes (as of June 2005) Day 1 - Crossing and Linking number 1. Definition and crossing number. (Reference: §§1.1 & 3.3 of [A]. References are listed at the end of these notes.) • Introduce idea of knot using physical representations (e.g., extension cord, rope, wire, chain, tangle toys). • Need to connect ends or else can undo knot; we’re allowed to do anything but cut. • The simplest knot is the unknot, but even this can look quite complicated. (Before class, scrunch up a big elastic band to make it look complicated. Then, in class, unravel it to illustrate that it’s the same as the unknot). • The next is the trefoil. There are two fairly simple projections which look quite different (demonstrate with extension cord). Figure 1: Two projections of the trefoil. Figure 2: How to get from one projection to the other. • We say the trefoil has crossing number three (we will write C(trefoil) = 3), since it has no projection with fewer than three crossings. We will prove this by showing projections of 0, 1, or 2 crossings are the unknot. Show that projections of 1 crossing are all the unknot. You may wish to identify projections that are the same up to rotation. In this case, there are four types of 1 Figure 3: Some 1-crossing projections. 1-crossing projection. If you also allow reflections, then there are only two types, one represented by the left column of Figure 3 and the other by any of the eight other projections. The crossing number two case is homework.
    [Show full text]