Problem of Points’’ and Their Histories
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Disability Classification System
CLASSIFICATION SYSTEM FOR STUDENTS WITH A DISABILITY Track & Field (NB: also used for Cross Country where applicable) Current Previous Definition Classification Classification Deaf (Track & Field Events) T/F 01 HI 55db loss on the average at 500, 1000 and 2000Hz in the better Equivalent to Au2 ear Visually Impaired T/F 11 B1 From no light perception at all in either eye, up to and including the ability to perceive light; inability to recognise objects or contours in any direction and at any distance. T/F 12 B2 Ability to recognise objects up to a distance of 2 metres ie below 2/60 and/or visual field of less than five (5) degrees. T/F13 B3 Can recognise contours between 2 and 6 metres away ie 2/60- 6/60 and visual field of more than five (5) degrees and less than twenty (20) degrees. Intellectually Disabled T/F 20 ID Intellectually disabled. The athlete’s intellectual functioning is 75 or below. Limitations in two or more of the following adaptive skill areas; communication, self-care; home living, social skills, community use, self direction, health and safety, functional academics, leisure and work. They must have acquired their condition before age 18. Cerebral Palsy C2 Upper Severe to moderate quadriplegia. Upper extremity events are Wheelchair performed by pushing the wheelchair with one or two arms and the wheelchair propulsion is restricted due to poor control. Upper extremity athletes have limited control of movements, but are able to produce some semblance of throwing motion. T/F 33 C3 Wheelchair Moderate quadriplegia. Fair functional strength and moderate problems in upper extremities and torso. -

National Classification? 13
NATIONAL CL ASSIFICATION INFORMATION FOR MULTI CLASS SWIMMERS Version 1.2 2019 PRINCIPAL PARTNER MAJOR PARTNERS CLASSIFICATION PARTNERS Version 1.2 2019 National Swimming Classification Information for Multi Class Swimmers 1 CONTENTS TERMINOLOGY 3 WHAT IS CLASSIFICATION? 4 WHAT IS THE CLASSIFICATION PATHWAY? 4 WHAT ARE THE ELIGIBLE IMPAIRMENTS? 5 CLASSIFICATION SYSTEMS 6 CLASSIFICATION SYSTEM PARTNERS 6 WHAT IS A SPORT CLASS? 7 HOW IS A SPORT CLASS ALLOCATED TO AN ATHLETE? 7 WHAT ARE THE SPORT CLASSES IN MULTI CLASS SWIMMING? 8 SPORT CLASS STATUS 11 CODES OF EXCEPTION 12 HOW DO I CHECK MY NATIONAL CLASSIFICATION? 13 HOW DO I GET A NATIONAL CLASSIFICATION? 13 MORE INFORMATION 14 CONTACT INFORMATION 16 Version 1.2 2019 National Swimming Classification Information for Multi Class Swimmers 2 TERMINOLOGY Assessment Specific clinical procedure conducted during athlete evaluation processes ATG Australian Transplant Games SIA Sport Inclusion Australia BME Benchmark Event CISD The International Committee of Sports for the Deaf Classification Refers to the system of grouping athletes based on impact of impairment Classification Organisations with a responsibility for administering the swimming classification systems in System Partners Australia Deaflympian Representative at Deaflympic Games DPE Daily Performance Environment DSA Deaf Sports Australia Eligibility Criteria Requirements under which athletes are evaluated for a Sport Class Evaluation Process of determining if an athlete meets eligibility criteria for a Sport Class HI Hearing Impairment ICDS International Committee of Sports for the Deaf II Intellectual Impairment Inas International Federation for Sport for Para-athletes with an Intellectual Disability General term that refers to strategic initiatives that address engagement of targeted population Inclusion groups that typically face disadvantage, including people with disability. -
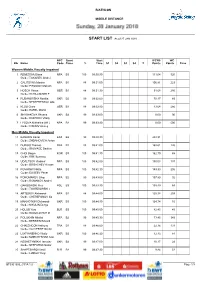
List Biathlon Middle Distance
BIATHLON MIDDLE DISTANCE START LIST As of 27 JAN 2018 NPC Sport Start IPCNS WC Bib Name Code Class % Time S1 S2 S3 S4 T Points Points Time Women Middle,Visually Impaired 1 REMIZOVA Elena NPA B3 100 09:30:30 111.04 320 Guide: TOKAREV Andrei 2 GALITSYNA Marina NPA B1 88 09:31:00 106.81 223 Guide: PIROGOV Maksim 3 HOSCH Vivian GER B1 88 09:31:30 91.68 280 Guide: SCHILLINGER F 4 RUBANOVSKA Natalia UKR B2 99 09:32:00 70.17 85 Guide: NESTERENKO Lada 5 KLUG Clara GER B1 88 09:32:30 13.64 280 Guide: HARTL Martin 6 SHYSHKOVA Oksana UKR B2 99 09:33:00 0.00 90 Guide: KAZAKOV Vitaliy 7 LYSOVA Mikhalina (WL) NPA B2 99 09:33:30 0.00 500 Guide: IVANOV Alexey Men Middle,Visually Impaired 11 KANAFIN Kairat KAZ B2 99 09:40:30 204.91 Guide: ZHDANOVICH Anton 12 DUBOIS Thomas FRA B1 88 09:41:00 168.61 126 Guide: SAUVAGE Bastien 13 CHOI Bogue KOR B3 100 09:41:30 162.70 65 Guide: KIM Hyunwoo 14 UDALTSOV Vladimir NPA B3 100 09:42:00 150.03 137 Guide: BOGACHEV Ruslan 15 POVAROV Nikita NPA B3 100 09:42:30 149.93 206 Guide: ELISEEV Pavel 16 PONOMAREV Oleg NPA B2 99 09:43:00 137.80 32 Guide: ROMANOV Andrei 17 GARBOWSKI Piotr POL B3 100 09:43:30 135.49 69 Guide: TWARDOWSKI J 18 ARTEMOV Aleksandr NPA B1 88 09:44:00 125.38 209 Guide: CHEREPANOV Ilia 19 MAKHOTKIN Oleksandr UKR B3 100 09:44:30 124.74 16 Guide: NIKULIN Denys 20 HOLUB Yury BLR B3 100 09:45:00 82.45 45 Guide: BUDZILOVICH D 21 POLUKHIN Nikolai NPA B2 99 09:45:30 73.45 345 Guide: BEREZIN Eduard 22 CHALENCON Anthony FRA B1 88 09:46:00 22.36 133 Guide: VALVERDE Simon 23 LUK'YANENKO Vitaliy UKR B3 100 09:46:30 -

(VA) Veteran Monthly Assistance Allowance for Disabled Veterans
Revised May 23, 2019 U.S. Department of Veterans Affairs (VA) Veteran Monthly Assistance Allowance for Disabled Veterans Training in Paralympic and Olympic Sports Program (VMAA) In partnership with the United States Olympic Committee and other Olympic and Paralympic entities within the United States, VA supports eligible service and non-service-connected military Veterans in their efforts to represent the USA at the Paralympic Games, Olympic Games and other international sport competitions. The VA Office of National Veterans Sports Programs & Special Events provides a monthly assistance allowance for disabled Veterans training in Paralympic sports, as well as certain disabled Veterans selected for or competing with the national Olympic Team, as authorized by 38 U.S.C. 322(d) and Section 703 of the Veterans’ Benefits Improvement Act of 2008. Through the program, VA will pay a monthly allowance to a Veteran with either a service-connected or non-service-connected disability if the Veteran meets the minimum military standards or higher (i.e. Emerging Athlete or National Team) in his or her respective Paralympic sport at a recognized competition. In addition to making the VMAA standard, an athlete must also be nationally or internationally classified by his or her respective Paralympic sport federation as eligible for Paralympic competition. VA will also pay a monthly allowance to a Veteran with a service-connected disability rated 30 percent or greater by VA who is selected for a national Olympic Team for any month in which the Veteran is competing in any event sanctioned by the National Governing Bodies of the Olympic Sport in the United State, in accordance with P.L. -

Official Rules
2018 Willamette Valley Youth Football & Cheer OFFICIAL RULES Page 1 Willamette Valley Youth Football & Cheer Table of Contents Part I – The WVYFC Program ............................................................... 5 Article 1: Members Code of Conduct ............................................. 5 Part II – WVYFC Structure .................................................................... 7 Part III – Regulations ............................................................................ 7 Article 1: Authority of League ......................................................... 7 Article 2: Boundaries ....................................................................... 7 Article 3: Coaches Requirements .................................................... 8 Article 4: Registration ..................................................................... 8 Article 5: Formation of Teams ........................................................ 9 Article 6: Mandatory Cuts ............................................................. 10 Article 7: Voluntary Cuts ............................................................... 10 Article 8: Certification ................................................................... 10 Article 9: Retention of Eligibility ................................................... 10 Article 10: No All Stars .................................................................. 10 Article 11: Awards ......................................................................... 11 Article 12: Practice (Definition & Date -

The Paralympic Athlete Dedicated to the Memory of Trevor Williams Who Inspired the Editors in 1997 to Write This Book
This page intentionally left blank Handbook of Sports Medicine and Science The Paralympic Athlete Dedicated to the memory of Trevor Williams who inspired the editors in 1997 to write this book. Handbook of Sports Medicine and Science The Paralympic Athlete AN IOC MEDICAL COMMISSION PUBLICATION EDITED BY Yves C. Vanlandewijck PhD, PT Full professor at the Katholieke Universiteit Leuven Faculty of Kinesiology and Rehabilitation Sciences Department of Rehabilitation Sciences Leuven, Belgium Walter R. Thompson PhD Regents Professor Kinesiology and Health (College of Education) Nutrition (College of Health and Human Sciences) Georgia State University Atlanta, GA USA This edition fi rst published 2011 © 2011 International Olympic Committee Blackwell Publishing was acquired by John Wiley & Sons in February 2007. Blackwell’s publishing program has been merged with Wiley’s global Scientifi c, Technical and Medical business to form Wiley-Blackwell. Registered offi ce: John Wiley & Sons, Ltd, The Atrium, Southern Gate, Chichester, West Sussex, PO19 8SQ, UK Editorial offi ces: 9600 Garsington Road, Oxford, OX4 2DQ, UK The Atrium, Southern Gate, Chichester, West Sussex, PO19 8SQ, UK 111 River Street, Hoboken, NJ 07030-5774, USA For details of our global editorial offi ces, for customer services and for information about how to apply for permission to reuse the copyright material in this book please see our website at www.wiley.com/wiley-blackwell The right of the author to be identifi ed as the author of this work has been asserted in accordance with the UK Copyright, Designs and Patents Act 1988. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, except as permitted by the UK Copyright, Designs and Patents Act 1988, without the prior permission of the publisher. -

Lecture 3: MIPS Instruction Set
Lecture 3: MIPS Instruction Set • Today’s topic: More MIPS instructions Procedure call/return • Reminder: Assignment 1 is on the class web-page (due 9/7) 1 Memory Operands • Values must be fetched from memory before (add and sub) instructions can operate on them Load word Register Memory lw $t0, memory-address Store word Register Memory sw $t0, memory-address How is memory-address determined? 2 Memory Address • The compiler organizes data in memory… it knows the location of every variable (saved in a table)… it can fill in the appropriate mem-address for load-store instructions int a, b, c, d[10] … Memory Base address 3 Immediate Operands • An instruction may require a constant as input • An immediate instruction uses a constant number as one of the inputs (instead of a register operand) addi $s0, $zero, 1000 # the program has base address # 1000 and this is saved in $s0 # $zero is a register that always # equals zero addi $s1, $s0, 0 # this is the address of variable a addi $s2, $s0, 4 # this is the address of variable b addi $s3, $s0, 8 # this is the address of variable c addi $s4, $s0, 12 # this is the address of variable d[0] 4 Memory Instruction Format • The format of a load instruction: destination register source address lw $t0, 8($t3) any register a constant that is added to the register in brackets 5 Example Convert to assembly: C code: d[3] = d[2] + a; Assembly: # addi instructions as before lw $t0, 8($s4) # d[2] is brought into $t0 lw $t1, 0($s1) # a is brought into $t1 add $t0, $t0, $t1 # the sum is in $t0 sw $t0, 12($s4) -

Classification Report
IPC Swimming Classification Master List Summer Season 2011 Classification Report created by IPC Sport Data Management System Sport: Swimming | Season: Summer Season 2011 | Region: Asian Region | NPC: China | Found Athletes: 115 China SDMS ID Family Name Given Name Gender Birth S St SB St SM St Review Exceptions 3389 Bai Juan W 1991 S4 C N/A C N/A C AE 12 5909 Bao Yanfen W 1991 S9 C SB9 C SM9 C 1,5 11938 Bi Tao M 1991 S10 C SB9 C SM10 C 9 6154 Cai Hong Mei W 1990 S10 C SB9 C SM10 C 8 16892 Cai Mengru W 1996 S3 C N/A N N/A N 8944 Cai Yuqingyan W 1995 S9 C SB8 C SM9 C 9 16893 Chen Handan W 1993 S3 C N/A N N/A N A 14535 Chen Jianfeng M 1985 S6 C SB7 C SM6 C AY 7 16901 Chen Lezhen M 1995 S4 C N/A N N/A N 5235 Chen Zhonglan W 1991 S8 C SB8 C SM8 C 1,3 4525 Cheng Jiao W 1994 S7 R SB6 R SM7 R 2011 12+ 16914 Dai Guohong M 1990 S7 C SB5 C SM7 C 6561 Deng Sanbo M 1987 S11 R SB11 R SM11 R TB 0 16887 Dong Ping M 1987 S3 C N/A N N/A N 3407 Du Jianping M 1983 S3 C SB2 C SM3 C A 1,2,12, 5527 Dun Longjuan W 1993 S9 C SB8 C SM9 C 9 16883 Feng Yazhu W 1992 S2 C N/A C A 4781 Gao Nan M 1989 S7 C SB7 C SM7 C 12+ 3637 Gu Kaixiang M 1991 S6 C SB5 C SM6 C A, 12+ 5266 Guan Xiangnan W 1987 S8 C SB8 C SM8 C A, 5, 12 5267 Guo Jun M 1988 S8 C SB8 C SM8 C 1,3, 5954 Guo Zhi M 1989 S9 C SB9 C SM9 C 1,4 3960 He Junquan M 1978 S5 C SB6 C SM5 C AY 7,9 8945 He Zhenxing W 1992 S9 C SB9 C SM9 C 1,5 4800 Hu Yu W 1989 S7 R SB7 R SM7 R 12+ 16900 Huang Chaowen M 1993 S4 N SB3 N SM4 N IPC Sport Data Management System Page 1 of 4 Timestamp 2015-08-27 03:35:52 IPC Swimming Classification -

Layman's Guide to Classification
LAYMAN’S GUIDE TO CLASSIFICATION Swimming is the only sport that combines the conditions of limb loss, cerebral palsy (coordination and movement restrictions), spinal cord injury (weakness or paralysis involving any combination of the limbs) and other disabilities, such as Dwarfism; major joint restriction condition across classes. • Classes S1-S10 – are allocated to swimmers with a physical impairment • Classes S11-S13 – are allocated to swimmers with a visual impairment • Class S14 – is allocated to swimmers with an intellectual impairment • Class S15 – is allocated to swimmers with a hearing impairment • The Prefix S to the Class denotes the class for Freestyle, Backstroke and Butterfly • The Prefix SB to the class denotes the class for Breaststroke • The Prefix SM to the class denotes the class for Individual Medley The range is from the swimmers with a more severe impairment (S1, SB1, SM1) to those with the impairment (S10, SB9, SM10) In any one class some swimmers may start with a dive or in the water depending on their impairment. This is factored in when classifying an athlete. The following examples are only a guide - some conditions not mentioned here may also fit the following classes THE FUNCTIONAL CLASSIFICATION SYSTEM (FCS) PHYSICAL IMPAIRMENTS S1, SB1, SM1 Swimmers in this class would usually be wheelchair users and may have a higher dependency for their every day needs. Examples: Swimmers with very severe coordination problems in all four limbs or have no use of their legs, trunk, hands and minimal use of their shoulders only. Swimmers in this class usually only swim on their back. -

Women Individual,Sitting Men Individual,Sitting BIATHLON LONG
BIATHLON LONG DISTANCE START LIST As of 26 JAN 2018 NPC Sport Start IPCNS WC Bib Name Code Class % Time S1 S2 S3 S4 T Points Points Time Women Individual,Sitting 1 LEE Doyeon KOR LW12 100 10:00:30 225.26 40 2 ABDIKARIMOVA Akzhana NPA LW10.5 90 10:01:00 124.28 116 3 KOCHEROVA Natalia NPA LW12 100 10:01:30 113.85 141 4 GRETSCH Kendall USA LW11.5 96 10:02:00 89.13 189 5 IOVLEVA Mariia NPA LW12 100 10:02:30 79.83 142 6 FEDOROVA Nadezhda NPA LW12 100 10:03:00 68.27 200 7 GULIAEVA Irina NPA LW12 100 10:03:30 29.56 240 8 ZAINULLINA Marta NPA LW12 100 10:04:00 19.92 256 9 HRAFEYEVA Lidziya BLR LW12 100 10:04:30 14.51 50 10 WICKER Anja GER LW10.5 90 10:05:00 4.12 124 11 MASTERS Oksana (WL) USA LW12 100 10:05:30 0.00 400 Men Individual,Sitting 21 KRAVCHUK Vasyl UKR LW11 94 10:20:30 15 22 FOGARASI Patrik GER LW11 94 10:21:00 10 23 USSOLTSEV Sergey KAZ LW12 100 10:21:30 315.33 32 24 ARNOLD Steve GBR LW12 100 10:22:00 290.02 9 25 FORTIER Sebastien CAN LW11.5 96 10:22:30 212.32 21 26 AMINOV Rustam NPA LW10 86 10:23:00 187.52 31 27 WON Yoomin KOR LW11.5 96 10:23:30 174.21 61 28 MEENAGH Scott GBR LW12 100 10:24:00 117.82 76 29 GANZEI Aleksandr NPA LW12 100 10:24:30 100.77 104 30 ZAPLOTINSKY Derek CAN LW10.5 90 10:25:00 95.81 78 31 DAVIDOVICH Aleksandr NPA LW12 100 10:25:30 87.57 182 32 LEE Jeong Min KOR LW12 100 10:26:00 69.77 87 33 CAMERON Collin CAN LW11.5 96 10:26:30 68.98 93 34 ROSIEK Kamil POL LW12 100 10:27:00 62.67 12 35 LUKYANENKA Yauheni BLR LW12 100 10:27:30 51.18 14 36 PIKE Aaron USA LW11.5 96 10:28:00 40.15 116 37 SOULE Andrew USA LW12 100 -

Supporting Information
Supporting Information Direct Synthesis of Bulk Boron-Doped Graphitic Carbon Nicholas P. Stadie, Emanuel Billeter, Laura Piveteau, Kostiantyn V. Kravchyk, Max Döbeli, and Maksym V. Kovalenko Contents: Tables S1-S3. Acquisition parameters for 11B and 13C NMR experiments Figure S1. Photographs of precursors and BC3′ product 13 Figure S2. C MAS NMR spectrum of BC3′ Figure S3. Raman spectroscopy of reference materials Figure S4. XRD comparison between tiled BC3′ and BC3′ (this work) Figure S5. SEM comparison between tiled BC3′ and BC3′ (this work) Figure S6. Raman spectroscopy comparison between tiled BC3′ and BC3′ (this work) Figure S7. Raman spectroscopy analysis of various BC3′ materials 11 Figure S8. B MAS NMR comparison between tiled BC3′ and BC3′ (this work) Figures S9-S10. ERDA comparison between tiled BC3′ and BC3′ (this work) Table S1. Acquisition parameters for 11B MQMAS NMR (Figure 5) Magnetic Field (T) 16.4 Temperature (K) 298 Rotor Diameter (mm) 2.5 Pulse Sequence mp3qdfs (Bruker) Number of Scans 1664 Recycle Delay (s) 0.6 Direct Dimension: 100 Spectral Width (kHz) Indirect Dimension: 125 Spinning Frequency (kHz) 20 Direct Dimension: 1024 Acquisition Length (points) Indirect Dimension: 256 Rotor Cycles for Synchronization 40 Indirect Dimension Increment (µs) 8.0 Split-t1 Increment (µs) 6.2 11B Excitation Pulse Width [π/2] (µs) 4.5 Double Frequency Sweep Length (µs) 12.5 11B Selective Pulse Width [π] (µs) 42 Table S2. Acquisition parameters for 11B MAS NMR (Figure S7) Magnetic Field (T) 16.4 Temperature (K) 298 Rotor Diameter (mm) 2.5 Pulse Sequence hahnecho (Bruker) Number of Scans 304 Recycle Delay (s) 1 Spectral Width (kHz) 100 Spinning Frequency (kHz) 20 Acquisition Length (points) 2048 11B 90° Pulse Width [π/2] (µs) 22 Table S3. -
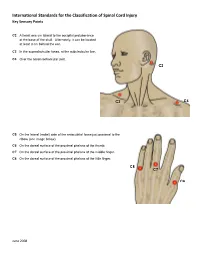
International Standards for the Classification of Spinal Cord Injury Key Sensory Points
International Standards for the Classification of Spinal Cord Injury Key Sensory Points C2 At least one cm lateral to the occipital protuberance at the base of the skull. Alternately, it can be located at least 3 cm behind the ear. C3 In the supraclavicular fossa, at the midclavicular line. C4 Over the acromioclavicular joint. C2 C3 C4 C5 On the lateral (radial) side of the antecubital fossa just proximal to the elbow (see image below). C6 On the dorsal surface of the proximal phalanx of the thumb. C7 On the dorsal surface of the proximal phalanx of the middle finger. C8 On the dorsal surface of the proximal phalanx of the little finger. C8 C7 C6 June 2008 International Standards for the Classification of Spinal Cord Injury Key Sensory Points C5 T2 T1 T1 On the medial (ulnar) side of the antecubital fossa, just proximal to the medial epicondyle of the humerus. T2 At the apex of the axilla. June 2008 International Standards for the Classification of Spinal Cord Injury Key Sensory Points T3 At the midclavicular line and the third intercostal space, found by palpating the anterior chest to locate the third C3 rib and the corresponding third intercostal space below it. T4 At the midclavicular line and the fourth intercostal space, located at the level of the nipples. T5 At the midclavicular line and the fifth intercostal space, located midway between the level of the nipples and T3 the level of the xiphisternum. T4 T6 At the midclavicular line, located at the level of the xiphisternum. T5 T7 At the midclavicular line, one quarter the distance between the level of T6 the xiphisternum and the level of the umbilicus.