Bipolar Ejections of Quasars from Galaxies
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

GTO Keypad Manual, V5.001
ASTRO-PHYSICS GTO KEYPAD Version v5.xxx Please read the manual even if you are familiar with previous keypad versions Flash RAM Updates Keypad Java updates can be accomplished through the Internet. Check our web site www.astro-physics.com/software-updates/ November 11, 2020 ASTRO-PHYSICS KEYPAD MANUAL FOR MACH2GTO Version 5.xxx November 11, 2020 ABOUT THIS MANUAL 4 REQUIREMENTS 5 What Mount Control Box Do I Need? 5 Can I Upgrade My Present Keypad? 5 GTO KEYPAD 6 Layout and Buttons of the Keypad 6 Vacuum Fluorescent Display 6 N-S-E-W Directional Buttons 6 STOP Button 6 <PREV and NEXT> Buttons 7 Number Buttons 7 GOTO Button 7 ± Button 7 MENU / ESC Button 7 RECAL and NEXT> Buttons Pressed Simultaneously 7 ENT Button 7 Retractable Hanger 7 Keypad Protector 8 Keypad Care and Warranty 8 Warranty 8 Keypad Battery for 512K Memory Boards 8 Cleaning Red Keypad Display 8 Temperature Ratings 8 Environmental Recommendation 8 GETTING STARTED – DO THIS AT HOME, IF POSSIBLE 9 Set Up your Mount and Cable Connections 9 Gather Basic Information 9 Enter Your Location, Time and Date 9 Set Up Your Mount in the Field 10 Polar Alignment 10 Mach2GTO Daytime Alignment Routine 10 KEYPAD START UP SEQUENCE FOR NEW SETUPS OR SETUP IN NEW LOCATION 11 Assemble Your Mount 11 Startup Sequence 11 Location 11 Select Existing Location 11 Set Up New Location 11 Date and Time 12 Additional Information 12 KEYPAD START UP SEQUENCE FOR MOUNTS USED AT THE SAME LOCATION WITHOUT A COMPUTER 13 KEYPAD START UP SEQUENCE FOR COMPUTER CONTROLLED MOUNTS 14 1 OBJECTS MENU – HAVE SOME FUN! -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -

Information Bulletin on Variable Stars
COMMISSIONS AND OF THE I A U INFORMATION BULLETIN ON VARIABLE STARS Nos April November EDITORS L SZABADOS K OLAH TECHNICAL EDITOR A HOLL TYPESETTING MB POCS ADMINISTRATION Zs KOVARI EDITORIAL BOARD E Budding HW Duerb eck EF Guinan P Harmanec chair D Kurtz KC Leung C Maceroni NN Samus advisor C Sterken advisor H BUDAPEST XI I Box HUNGARY URL httpwwwkonkolyhuIBVSIBVShtml HU ISSN 2 IBVS 4701 { 4800 COPYRIGHT NOTICE IBVS is published on b ehalf of the th and nd Commissions of the IAU by the Konkoly Observatory Budap est Hungary Individual issues could b e downloaded for scientic and educational purp oses free of charge Bibliographic information of the recent issues could b e entered to indexing sys tems No IBVS issues may b e stored in a public retrieval system in any form or by any means electronic or otherwise without the prior written p ermission of the publishers Prior written p ermission of the publishers is required for entering IBVS issues to an electronic indexing or bibliographic system to o IBVS 4701 { 4800 3 CONTENTS WOLFGANG MOSCHNER ENRIQUE GARCIAMELENDO GSC A New Variable in the Field of V Cassiop eiae :::::::::: JM GOMEZFORRELLAD E GARCIAMELENDO J GUARROFLO J NOMENTORRES J VIDALSAINZ Observations of Selected HIPPARCOS Variables ::::::::::::::::::::::::::: JM GOMEZFORRELLAD HD a New Low Amplitude Variable Star :::::::::::::::::::::::::: ME VAN DEN ANCKER AW VOLP MR PEREZ D DE WINTER NearIR Photometry and Optical Sp ectroscopy of the Herbig Ae Star AB Au rigae ::::::::::::::::::::::::::::::::::::::::::::::::::: -
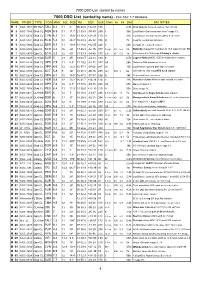
DSO List V2 Current
7000 DSO List (sorted by name) 7000 DSO List (sorted by name) - from SAC 7.7 database NAME OTHER TYPE CON MAG S.B. SIZE RA DEC U2K Class ns bs Dist SAC NOTES M 1 NGC 1952 SN Rem TAU 8.4 11 8' 05 34.5 +22 01 135 6.3k Crab Nebula; filaments;pulsar 16m;3C144 M 2 NGC 7089 Glob CL AQR 6.5 11 11.7' 21 33.5 -00 49 255 II 36k Lord Rosse-Dark area near core;* mags 13... M 3 NGC 5272 Glob CL CVN 6.3 11 18.6' 13 42.2 +28 23 110 VI 31k Lord Rosse-sev dark marks within 5' of center M 4 NGC 6121 Glob CL SCO 5.4 12 26.3' 16 23.6 -26 32 336 IX 7k Look for central bar structure M 5 NGC 5904 Glob CL SER 5.7 11 19.9' 15 18.6 +02 05 244 V 23k st mags 11...;superb cluster M 6 NGC 6405 Opn CL SCO 4.2 10 20' 17 40.3 -32 15 377 III 2 p 80 6.2 2k Butterfly cluster;51 members to 10.5 mag incl var* BM Sco M 7 NGC 6475 Opn CL SCO 3.3 12 80' 17 53.9 -34 48 377 II 2 r 80 5.6 1k 80 members to 10th mag; Ptolemy's cluster M 8 NGC 6523 CL+Neb SGR 5 13 45' 18 03.7 -24 23 339 E 6.5k Lagoon Nebula;NGC 6530 invl;dark lane crosses M 9 NGC 6333 Glob CL OPH 7.9 11 5.5' 17 19.2 -18 31 337 VIII 26k Dark neb B64 prominent to west M 10 NGC 6254 Glob CL OPH 6.6 12 12.2' 16 57.1 -04 06 247 VII 13k Lord Rosse reported dark lane in cluster M 11 NGC 6705 Opn CL SCT 5.8 9 14' 18 51.1 -06 16 295 I 2 r 500 8 6k 500 stars to 14th mag;Wild duck cluster M 12 NGC 6218 Glob CL OPH 6.1 12 14.5' 16 47.2 -01 57 246 IX 18k Somewhat loose structure M 13 NGC 6205 Glob CL HER 5.8 12 23.2' 16 41.7 +36 28 114 V 22k Hercules cluster;Messier said nebula, no stars M 14 NGC 6402 Glob CL OPH 7.6 12 6.7' 17 37.6 -03 15 248 VIII 27k Many vF stars 14.. -

Resolving the Ultra-Luminous X-Ray Sources in the Ly $\Alpha $ Emitting
MNRAS 000,1–16 (2020) Preprint 11 May 2021 Compiled using MNRAS LATEX style file v3.0 Resolving the Ultra-Luminous X-ray Sources in the LyU Emitting Galaxy Haro 11 Arran C. Gross,1¢ Andrea Prestwich,2 Philip Kaaret1 1Department of Physics and Astronomy, University of Iowa, Van Allen Hall, Iowa City, IA 52242, USA 2Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA Accepted XXX. Received YYY; in original form ZZZ ABSTRACT Lyman continuum and line emission are thought to be important agents in the reionization of the early universe. Haro 11 is a rare example of a local galaxy in which LyU and continuum emission have escaped without being absorbed or scattered by ambient gas and dust, potentially as a consequence of feedback from its X-ray sources. We build on our previous Chandra analysis of Haro 11 by analyzing three new observations. Our subpixel spatial analysis reveals that the two previously known X-ray sources are each better modelled as ensembles of at least 2 unresolved point sources. The spatial variability of these 41 −1 components reveals X1 as a dynamical system where one luminous X-ray source (!X ∼ 10 erg s ) fades as a secondary source begins to flare. These might be intermediate mass black holes or low luminosity active galactic nuclei near the center of the galaxy in the process of merging. Optical emission line diagnostics drawn from the literature suggest that while the galaxy as a whole is consistent with starburst signatures of ionization, the individual regions wherein the X-ray sources reside are more consistent with AGN/composite classification. -

The Observer's Handbook 1959
THE OBSERVER’S HANDBOOK 1959 Fifty-first Year of Publication THE ROYAL ASTRONOMICAL SOCIETY OF CANADA Price 75 cents THE ROYAL ASTRONOMICAL SOCIETY OF CANADA Incorporated 1890 — Royal Charter 1903 The National Headquarters of the Royal Astronomical Society of Canada is located at 252 College Street, Toronto 2B, Ontario. The business office of the Society, reading rooms and astronomical library, are housed here, as well as a large room for the accommodation of telescope making groups. Membership in the Society is open to anyone interested in astronomy. Applicants may affiliate with one of the Society's fourteen centres across Canada, or may join the National Society. Centres of the Society are established in Halifax, Quebec, Montreal, Ottawa, Hamilton, London, Windsor, Winnipeg, Edmonton, Calgary, Vancouver, Victoria, and Toronto. Addresses of the Centres' secretaries may be obtained from the National Headquarters. Publications of the Society are free to members, and include the Jo urnal (6 issues per year) and the O bserver's H andbook (published annually in November). Annual fees of $5.00 are payable October 1 and include the publications for the following year. Requests for additional information regarding the Society or its publications may be sent to the address above. Communications to the Editor should be sent to Miss Ruth J. Northcott, David Dunlap Observatory, Richmond Hill, Ontario. Visiting Hours at some Canadian Observatories Dominion Observatory, Ottawa, Ont.: Monday to Friday, daytime, rotunda only. Saturday evenings, April through October. The 15-inch telescope is used for visitors and one of the five divisions of the Observatory is open. David Dunlap Observatory, Richmond Hill, Ont.: Wednesday afternoons. -

Cvn – Objektauswahl NGC Seite 1
CVn – Objektauswahl NGC Seite 1 NGC 4109 NGC 4151 NGC 4220 NGC 4288 NGC 4449 NGC 4619 NGC 4707 NGC 4846 NGC 4956 NGC 4111 NGC 4156 NGC 4226 NGC 4346 NGC 4460 NGC 4625 NGC 4711 NGC 4861 NGC 4959 NGC 4117 NGC 4163 NGC 4227 NGC 4357 NGC 4485 NGC 4627 NGC 4719 NGC 4868 NGC 4963 Seite 2 NGC 4118 NGC 4229 NGC 4369 NGC 4490 NGC 4631 NGC 4736 NGC 4870 NGC 4985 NGC 4135 NGC 4183 NGC 4231 NGC 4389 NGC 4509 NGC 4655 NGC 4737 NGC 4893 NGC 4986 Seite 3 NGC 4137 NGC 4187 NGC 4232 NGC 4392 NGC 4534 NGC 4656 NGC 4741 NGC 4901 NGC 4987 NGC 4138 NGC 4190 NGC 4242 NGC 4395 NGC 4542 NGC 4657 NGC 4774 NGC 4914 NGC 4998 NGC 4143 NGC 4214 NGC 4244 NGC 4399 NGC 4583 NGC 4662 NGC 4800 NGC 4917 NGC 5002 NGC 4145 NGC 4217 NGC 4248 NGC 4400 NGC 4617 NGC 4687 NGC 4834 NGC 4932 NGC 5003 NGC 4148 NGC 4218 NGC 4258 NGC 4401 NGC 4618 NGC 4704 NGC 4837 NGC 4938 NGC 5005 Sternbild- Zur Objektauswahl: Nummer anklicken Übersicht Zur Übersichtskarte: Objekt in Aufsuchkarte anklicken Zum Detailfoto: Objekt in Übersichtskarte anklicken CVn – Objektauswahl NGC Seite 2 NGC 5009 NGC 5083 NGC 5131 NGC 5173 NGC 5229 NGC 5272 NGC 5290 NGC 5319 NGC 5349 NGC 5014 NGC 5093 NGC 5141 NGC 5187 NGC 5233 NGC 5273 NGC 5296 NGC 5320 NGC 5350 Seite 1 NGC 5021 NGC 5096 NGC 5142 NGC 5194 NGC 5238 NGC 5274 NGC 5297 NGC 5321 NGC 5351 NGC 5023 NGC 5098 NGC 5143 NGC 5195 NGC 5240 NGC 5275 NGC 5301 NGC 5325 NGC 5352 NGC 5025 NGC 5103 NGC 5145 NGC 5198 NGC 5243 NGC 5276 NGC 5303 NGC 5326 NGC 5353 Seite 3 NGC 5029 NGC 5107 NGC 5149 NGC 5199 NGC 5259 NGC 5277 NGC 5305 NGC 5336 NGC 5354 NGC 5033 NGC 5112 -

DSO List V2 Current
7000 DSO List (sorted by constellation - magnitude) 7000 DSO List (sorted by constellation - magnitude) - from SAC 7.7 database NAME OTHER TYPE CON MAG S.B. SIZE RA DEC U2K Class ns bs SAC NOTES M 31 NGC 224 Galaxy AND 3.4 13.5 189' 00 42.7 +41 16 60 Sb Andromeda Galaxy;Local Group;nearest spiral NGC 7686 OCL 251 Opn CL AND 5.6 - 15' 23 30.1 +49 08 88 IV 1 p 20 6.2 H VIII 69;12* mags 8...13 NGC 752 OCL 363 Opn CL AND 5.7 - 50' 01 57.7 +37 40 92 III 1 m 60 9 H VII 32;Best in RFT or binocs;Ir scattered cl 70* m 8... M 32 NGC 221 Galaxy AND 8.1 12.4 8.5' 00 42.7 +40 52 60 E2 Companion to M31; Member of Local Group M 110 NGC 205 Galaxy AND 8.1 14 19.5' 00 40.4 +41 41 60 SA0 M31 Companion;UGC 426; Member Local Group NGC 272 OCL 312 Opn CL AND 8.5 - 00 51.4 +35 49 90 IV 1 p 8 9 NGC 7662 PK 106-17.1 Pln Neb AND 8.6 5.6 17'' 23 25.9 +42 32 88 4(3) 14 Blue Snowball Nebula;H IV 18;Barnard-cent * variable? NGC 956 OCL 377 Opn CL AND 8.9 - 8' 02 32.5 +44 36 62 IV 1 p 30 9 NGC 891 UGC 1831 Galaxy AND 9.9 13.6 13.1' 02 22.6 +42 21 62 Sb NGC 1023 group;Lord Rosse drawing shows dark lane NGC 404 UGC 718 Galaxy AND 10.3 12.8 4.3' 01 09.4 +35 43 91 E0 Mirach's ghost H II 224;UGC 718;Beta AND sf 6' IC 239 UGC 2080 Galaxy AND 11.1 14.2 4.6' 02 36.5 +38 58 93 SBa In NGC 1023 group;vsBN in smooth bar;low surface br NGC 812 UGC 1598 Galaxy AND 11.2 12.8 3' 02 06.9 +44 34 62 Sbc Peculiar NGC 7640 UGC 12554 Galaxy AND 11.3 14.5 10' 23 22.1 +40 51 88 SBbc H II 600;nearly edge on spiral MCG +08-01-016 Galaxy AND 12 - 1.0' 23 59.2 +46 53 59 Face On MCG +08-01-018 -

High Resolution IR Observations of the Starburst Ring in NGC 7552
Astronomy & Astrophysics manuscript no. NGC7552˙Brandl c ESO 2018 November 9, 2018 High Resolution IR Observations of the Starburst Ring in NGC 7552 One Ring to Rule Them All? B. R. Brandl1, N. L. Mart´ın-Hern´andez2,3 , D. Schaerer4,5, M. Rosenberg1, and P. P. van der Werf1 1 Leiden Observatory, Leiden University, P.O. Box 9513, NL-2300 RA Leiden, Netherlands 2 Instituto de Astrof´ısica de Canarias, V´ıa L´actea s/n, E-38205 La Laguna, Spain 3 Departamento de Astrof´ısica, Universidad de La Laguna, E-38205 La Laguna, Tenerife, Spain 4 Geneva Observatory, University of Geneva, 51, Ch. des Maillettes, CH-1290 Versoix, Switzerland 5 CNRS, IRAP, 9 Av. colonel Roche, BP 44346, F-31028 Toulouse cedex 4, France Received June 26, 2011; accepted May 4, 2012 ABSTRACT Aims. Approximately 20% of all spiral galaxies display starburst activity in nuclear rings of a few hundred parsecs in diameter. It is our main aim to investigate how the starburst ignites and propagates within the ring, leading to the formation of massive stellar clusters. Methods. We observed the ring galaxy NGC 7552 with the mid-infrared (MIR) instrument VISIR at an angular resolution of 0′′. 3−0′′. 4 and with the near-infrared (NIR) integral-field spectrograph SINFONI on the VLT, and complement these observations with data from ISO and Spitzer. Results. The starburst ring is clearly detected at MIR wavelengths at the location of the dust-extincted, dark ring seen in HST observations. This “ring”, however, is a rather complex annular region of more than 100 parsec width. -

The Northern ROSAT All-Sky (NORAS) Galaxy Cluster Survey I: X
The Northern ROSAT All-Sky (NORAS) Galaxy Cluster Survey I: X-ray Properties of Clusters Detected as Extended X-ray Sources 1 H. B¨ohringer1, W. Voges1, J.P. Huchra2,B. McLean3, R. Giacconi4, P. Rosati4, R. Burg3, J. Mader2, P. Schuecker1, D. Simi¸c1, S. Komossa1, T.H. Reiprich1, J. Retzlaff1, J. Tr¨umper1 Received ; accepted arXiv:astro-ph/0003219v2 22 Mar 2000 1Results reported here are based on observations made with the Multiple Mirror Telescope, a joint facility of the Smithonian Institution and the University of Arizona 1Max-Planck-Institut f¨ur extraterrestrische Physik, D-85740 Garching,Germany 2Harvard-Smithonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 0213 4Space Telescope Science Institute, San Martin Drive, Baltimore, MA 02138 3ESO, D-85748 Garching,Germany –2– ABSTRACT In the construction of an X-ray selected sample of galaxy clusters for cosmological studies, we have assembled a sample of 495 X-ray sources found to show extended X-ray emission in the first processing of the ROSAT All-Sky Survey. The sample covers the celestial region with declination δ ≥ 0◦ and ◦ galactic latitude |bII| ≥ 20 and comprises sources with a count rate ≥ 0.06 counts s−1 and a source extent likelihood of 7. In an optical follow-up identification program we find 378 (76%) of these sources to be clusters of galaxies. It was necessary to reanalyse the sources in this sample with a new X-ray source characterization technique to provide more precise values for the X-ray flux and source extent than obtained from the standard processing. -
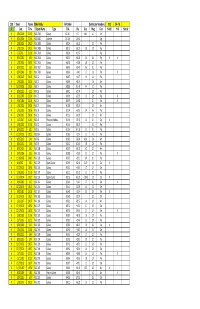
MX Date Time Object Name Type RA Dec Size Mag Con H-400 H-II
2382 : Count Name: Mike Hotka RA Order Certificate Numbers: 303 54 - M X Date Time Object Name Type R.A. Dec Size Mag Con H-400 H-II Hustle X 3/31/2019 21:53 NGC 4366 Galaxy 12:24.5 +7.3 .9x.6 14.3 Vir X 9/24/2016 21:34 NGC 6561 Asterism 18:10.5 -16:43 Sgr X 1/18/2015 20:23 NGC 7805 Galaxy 0:01.4 +31:26 13.3 Peg X 1/18/2015 20:23 NGC 7806 Galaxy 0:01.5 +31:27 1.9 13.5 Peg X 1/7/2012 21:09 NGC 7810 Galaxy 0:02.4 +12:57 Peg X 8/11/2002 0:56 NGC 7814 Galaxy 0:03.3 +16:09 2.6 10.6 Peg X X X 1/18/2015 20:55 NGC 7816 Galaxy 0:03.8 +7:28 1.8 12.8 Psc X 8/19/2012 1:16 NGC 7817 Galaxy 0:04.0 +20:45 4.6 11.8 Peg X 9/30/2006 0:50 NGC 7832 Galaxy 0:06.6 -3:42 1.7 13.8 Psc X X 1/18/2015 20:05 NGC 12 Galaxy 0:08.7 +4:37 1.9 14.1 Psc X 1/18/2005 20:26 NGC 13 Galaxy 0:08.8 +33:26 13.6 And X 10/27/2008 19:55 NGC 14 Galaxy 0:08.8 +15:49 4.4 12.1 Peg X 8/19/2012 1:12 NGC 16 Galaxy 0:09.1 +27:44 12.0 Peg X 9/19/2006 23:06 NGC 23 Galaxy 0:09.9 +25:55 2.3 12.0 Peg X X 9/19/2006 23:18 NGC 24 Galaxy 0:09.9 -24:58 11.5 Scl X X 1/18/2015 20:28 NGC 29 Galaxy 0:10.8 +33:21 12.6 And X 1/18/2015 20:06 NGC 36 Galaxy 0:11.4 +6:23 2.4 14.4 Psc X 1/18/2015 20:30 NGC 39 Galaxy 0:12.3 +31:03 13.5 And X 11/2/2007 21:45 NGC 40 Planetary Nebula 0:13.0 +72:32 0.3 10.7 Cep X X 1/18/2015 21:16 NGC 52 Galaxy 0:14.6 +18:33 13.3 Peg X 8/19/2012 3:01 NGC 57 Galaxy 0:15.4 +17:18 4.1 11.6 Psc X 12/27/2013 18:21 NGC 61A Galaxy 0:16.5 -6:14 1.1 14.7 Psc X 8/19/2012 1:44 NGC 68 Galaxy 0:18.3 +30:04 62.0 13.0 And X 8/19/2012 2:58 NGC 95 Galaxy 0:22.2 +10:30 7.8 12.6 Psc X 8/19/2012 1:41 -

National Solar Observatory (NSO)—Has Prepared Separate Quarterly Reports Which Are Included in This Packet
NATIONAL OPTICAL ASTRONOMY OBSERVATORIES QUARTERLY REPORT January 1, 1984 - March 31, 1984 The period ending March 31, 1984, was a very active period with the formation of NOAO and several of its component parts. Each of the Observatories—Cerro Tololo Inter-American Observatory (CTIO), Kitt Peak National Observatory (KPNO), and National Solar Observatory (NSO)—has prepared separate quarterly reports which are included in this packet. Because the Advanced Development Program (ADP) was just starting up during the last month of the reporting period, a report was not required for that division. The only other units which were formed during the reporting period—the NOAO Director's Office and Central Administrative Services—are covered in the following report (Central Offices). Director's Office The NOAO Director's Office was officially established on February 1, 1984. During this first quarter efforts were centered on reorganization of the management of the three ground- based observatories—CTIO, KPNO, and NSO—and the formation of the NOAO Central Offices. Search Committees which we established for the NOAO Associate Directors/Directors of KPNO and NSO completed their separate searches and recommended candidates for the positions. Consistent with their recommendation Drs. Sidney Wolff and Robert Howard were selected by NOAO Director Jefferies, for KPNO and NSO respectively, for recommendation to the AURA Executive Committee whose approval was subsequently obtained. In addition, selections were made for the following positions: NOAO Associate Director/Director ADP, Manager Central Administrative Services/Controller, Assistant to the Director NOAO, Manager of NOAO Engineering and Technical Services, and Manager of NOAO Central Computer Services.