DOCSLIB.ORG

Elementary Algebra Review

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Elementary Algebra Review Placement Test Review Materials for 1 To The Student This workbook will provide a review of some of the skills tested on the COMPASS placement test. Skills covered in this workbook will be used on the Algebra section of the placement test. This workbook is a review and is not intended to provide detailed instruction. There may be skills reviewed that you will not completely understand. Just like there will be math problems on the placement tests you may not know how to do. Remember, the purpose of this review is to allow you to “brush-up” on some of the math skills you have learned previously. The purpose is not to teach new skills, to teach the COMPASS placement test or to allow you to skip basic classes that you really need. The Algebra test will assess you r mastery of operations using signed numbers and evaluating numerical and algebraic expressions. This test will also assess your knowledge of equations solving skills used to solve 1-variable equations and inequalities, solve verbal problems, apply formulas, solve a formula fro a particular variable, and fined “k” before you find the answer. You will also be tested on your knowledge of exponents, scientific notation, and radical expressions, as well as operations on polynomials. Furthermore, other elementary algebra skills that will be on the test include factoring polynomials, and using factoring to solve quadratic equations and simplify, multiply, and divide rational expressions. 2 Table of Contents Evaluating Expressions Using Order of Operations 4 Simplifying Complex Fractions 5 Evaluating Algebraic Expressions 6 Using Formulas 8 Solving Equations Solving 1-Variable Equations 9 Solving 1-Variable Inequalities 12 Writing Verbal Expressions as Equations and Algebraic Expressions 13 Solving an Equation for a Particular Variable 15 Solving Problems that Involve a Second Variable 16 Using Exponents Using the Rules for Exponents to Simplify 17 Using Scientific Notation 19 Simplifying Polynomials Adding and Subtracting Polynomials 20 Multiplying Polynomials 21 Using Factoring Factoring Polynomials 22 Solving Quadratic Equations Using Factoring 26 Applying Quadratic Equations 28 Simplifying Rational Expressions 29 Multiplying and Dividing Rational Expressions 30 Using Radicals Simplifying Radical Expressions 31 Adding, Subtracting, Multiplying and Dividing Radical Expressions 33 Answer Key 34 3 4 Using Order of Operations Rules: 1. Do the operation inside the parentheses, braces, brackets, or absolute value first. If more than one, do the innermost parentheses first. 2. Do the exponents next. 3. Multiply and Divide from left to right. 4. Add and Subtract from left to right. Examples: 5 + 3(8 – 9) – 7 = 52 – 3(7 + 2) ÷ 27 = 5 + 3(8 + -9) + -7 = 52 + -3 (9) ÷ 27 = 5 + 3(-1) + -7 = 25 + -3(9) ÷ 27 = 2 + -7 = -5 25 + -27 ÷ 27 = 25 + -1 = 24 WATCH OUT! 3( 2) 5 In an expression like , the fraction bar acts like a grouping symbol. Simplify 7 2( 2) the numerator and denominator separately, and then divide. Practice: 1. Simplify: 8 ÷ 23 – 12 ÷ 22 2. Simplify: 2 · 42 – 6 ÷ 2 – 9 · 4 36( 6) 3. Evaluate: 14 – 27 ÷ (3 – 6)2 – 3 4. Evaluate: 4(2 5)2 5 Simplifying Complex Fractions Simplify the numerator and the denominator first, and then divide the numerator by the denominator. 3 9 15 18 33 33 2 33 Example: 4 10 20 20 20 1 5 5 2 20 5 50 2 2 2 Practice: 3 1 4 1. Simplify: 2. Simplify: 5 13 1 1 38 10 21 23 34 34 3. Evaluate: 4. Evaluate: 2 5 1 7 2 6 Evaluating Algebraic Expressions Substitute the value(s) for the variable(s). If the value is a negative number, use a parentheses around the number. This will help prevent mistakes with negative signs. Use order of operations to simplify. Examples: Evaluate: -4(a – 2b) – bc for a = 3, b = -2 and c = 4. -4(a – 2b) – bc = -4(3 – 2(-2)) – (-2)4 = -4(3 – (-4)) – (-8) = -4(3 + 4) + 8 = -4(7) + 8 = -28 + 8 = -20 Find the value of 3x2 – x + 2 when x = -2. 3x2 – x + 2 = 3(-2)2 –(-2) + 2 = 3(4) + 2 + 2 = 12 + 2 + 2 = 16 Practice: 21 1. Evaluate a2 – b2 when a = 4 and b = -3. 2. Evaluate: x( xy 4 x ) when x = -6 32 and y = 3. 11 3. Evaluate -2a2 + 3b – c when a = -3, 4. Evaluate: mn22 when m = 3 34 b = 2, and c = 4. and n = 8. 7 5. Find the value of –x5 + 4x2 -9x -7 6. Evaluate the following polynomial for for x = -1. y = -1. 3y2 – y + 5 8 Using Formulas Read the problem carefully. Identify the known and unknown variables. Write a formula that relates the variable in the problem Substitute the known values for the variables. Solve the equation and answer the question. Example: Find the length of weather stripping needed to put around a rectangular window that is 9 ft. wide and 22 ft. long. The perimeter of a rectangle is found by using the formula: P = 2L + 2W, L = length and W = width. Known variables: W = 9, L = 22 Formula: P = 2L + 2W Unknown variable: P P = 2(22) + 2(9) P = 44 + 18 P = 62 ft. Practice: 1. Find the length of aluminum framing needed to frame a picture that is 6 ft. by 4 ft. The formula for the perimeter of a rectangle is P = 2L + 2W, where L = length and W = width. 2. Find the approximate length of a rubber gasket needed to fit around a circular porthole that has a 20-inch diameter. The formula for the circumference of a circle is C = π · d, where d = diameter. Use π = 3.14. 9 3. A room 11 ft. by 15 ft. is to be carpeted. Find the number of square yards of carpet needed (9ft2 = 1 yd2). Round to the nearest tenth. 4. The surface area of a right circular cylinder can be found by using the formula: SA = 2πrh + 2πr2. Use the formula to find the surface area of an oil drum whose radius is 4 ft. and whose height is 5 ft. Use π = 3.14. 10 Solving 1-Variable Equations An equation is a mathematical sentence that involves an equal sign. Examples of equations in one variable are: 3x – 6 = 9 2x + 5x – 8 = 5x – 3 3(x – 2) = 5x + 6 The following steps are used to solve an equation: 1. Remove parentheses and combine like terms on each side of the “=”. 2. Use the addition property to get all terms with variables on one side of the equation and all other terms on the other side. (Remember, if you add a term to one side of the equation, then you must add the same term to the other side to keep the equation balanced or true. 3. Combine like terms on each side of the equation. 4. Use the multiplication or division property to solve for the variable. Remember to multiply or divide both sides in order to keep the equation balanced or true. 5. Check your solution for the variable by substituting into the original equation and simplifying. The result should be a true statement. Examples: Solve: 3x – 8 = 4 Solve: 3(x + 5) + 2x = 6x + 10 3x + -8 = 4 3x +15 +2x = 6x + 10 3x + -8 + 8 = 4 + 8 5x + 15 = 6x + 10 3x = 12 5x + -6x + 15 = 6x + -6x + 10 3x = 12 -1x + 15 = 10 3 3 -1x + 15 + -15 = 10 + -15 x = 4 -1x = -5 -1 -1 x = 5 Practice: 1. Solve: 5x – 5 = 3x + 7 2. Solve: 2x – 11 = -3x + 9 11 3. Solve: 5x + 7 + 3x = 47 4. Solve: 4y + 6 + y = 11 5 1 5. Solve: x 35 6. Solve: x 52 8 3 7. Solve: 2x – 3(2x – 5) = 7 – 2x 8. Solve: 3x + 4(2x – 7) = 9x – 22 12 Solving 1-Variable Inequalities To solve an inequality, you follow the same rules that you use for solving an equation except: When you multiply or divide both sides by a negative number, you must change the inequality sign. Examples: Solve: 2x + 6 > 4 Solve: -3x + 8 > -4 2x + 6 + (-6) > 4 + (-6) -3x + 8 + (-8) > -4 + (-8) 2x > -2 -3x > -12 2x > -2 -3x > -12 2 2 -3 -3 x > -1 x < 4 (did not change > sign) (did change > to < because I divided by a negative number) Practice: 1. -5x + 2 < -18 2. 3x – 2 > 13 3. Solve: 5x – 1 < -9 4. Solve: 2 – 7x < 16 13 Writing Verbal Expressions as Equations and Algebraic Expressions Words that mean add: Words that mean subtract: plus total minus reduced by sum greater than fewer difference between increased by more than decreased by less than Words that mean multiply: Words that mean divide: times product of quotient of divisor of at (sometimes) dividend ratio total(sometimes) parts Examples: Translate into an algebraic expression or equation: three more than twice a number 2n + 3 eight less than 1/3 of a number 1/3n – 8 four times a number increased by 6 4n + 6 the product of a number and 5 5n Translate into an equation or inequality. Then solve: Four more than three times a number equals 8. 3n + 4 = 8 3n + 4 + (-4) = 8 + (-4) 3n = 4 3n = 4 3 3 n = 4/3 The difference between twice a number and 3 is greater than 15. 2x – 3 > 15 2x + (-3) + 3 > 15 + 3 2x > 18 2x > 18 2 2 x > 9 14 Practice: 1. Translate “six less than the product of n and negative nine” into an algebraic expression: 2. Write “the quotient of ten and the sum of a number and 7 as an algebraic expression 3.
Load more

Recommended publications
  • Solving Equations; Patterns, Functions, and Algebra; 8.15A
    Mathematics Enhanced Scope and Sequence – Grade 8 Solving Equations Reporting Category Patterns, Functions, and Algebra Topic Solving equations in one variable Primary SOL 8.15a The student will solve multistep linear equations in one variable with the variable on one and two sides of the equation. Materials • Sets of algebra tiles • Equation-Solving Balance Mat (attached) • Equation-Solving Ordering Cards (attached) • Be the Teacher: Solving Equations activity sheet (attached) • Student whiteboards and markers Vocabulary equation, variable, coefficient, constant (earlier grades) Student/Teacher Actions (what students and teachers should be doing to facilitate learning) 1. Give each student a set of algebra tiles and a copy of the Equation-Solving Balance Mat. Lead students through the steps for using the tiles to model the solutions to the following equations. As you are working through the solution of each equation with the students, point out that you are undoing each operation and keeping the equation balanced by doing the same thing to both sides. Explain why you do this. When students are comfortable with modeling equation solutions with algebra tiles, transition to writing out the solution steps algebraically while still using the tiles. Eventually, progress to only writing out the steps algebraically without using the tiles. • x + 3 = 6 • x − 2 = 5 • 3x = 9 • 2x + 1 = 9 • −x + 4 = 7 • −2x − 1 = 7 • 3(x + 1) = 9 • 2x = x − 5 Continue to allow students to use the tiles whenever they wish as they work to solve equations. 2. Give each student a whiteboard and marker. Provide students with a problem to solve, and as they write each step, have them hold up their whiteboards so you can ensure that they are completing each step correctly and understanding the process.
    [Show full text]
  • Diffman: an Object-Oriented MATLAB Toolbox for Solving Differential Equations on Manifolds
    Applied Numerical Mathematics 39 (2001) 323–347 www.elsevier.com/locate/apnum DiffMan: An object-oriented MATLAB toolbox for solving differential equations on manifolds Kenth Engø a,∗,1, Arne Marthinsen b,2, Hans Z. Munthe-Kaas a,3 a Department of Informatics, University of Bergen, N-5020 Bergen, Norway b Department of Mathematical Sciences, NTNU, N-7491 Trondheim, Norway Abstract We describe an object-oriented MATLAB toolbox for solving differential equations on manifolds. The software reflects recent development within the area of geometric integration. Through the use of elements from differential geometry, in particular Lie groups and homogeneous spaces, coordinate free formulations of numerical integrators are developed. The strict mathematical definitions and results are well suited for implementation in an object- oriented language, and, due to its simplicity, the authors have chosen MATLAB as the working environment. The basic ideas of DiffMan are presented, along with particular examples that illustrate the working of and the theory behind the software package. 2001 IMACS. Published by Elsevier Science B.V. All rights reserved. Keywords: Geometric integration; Numerical integration of ordinary differential equations on manifolds; Numerical analysis; Lie groups; Lie algebras; Homogeneous spaces; Object-oriented programming; MATLAB; Free Lie algebras 1. Introduction DiffMan is an object-oriented MATLAB [24] toolbox designed to solve differential equations evolving on manifolds. The current version of the toolbox addresses primarily the solution of ordinary differential equations. The solution techniques implemented fall into the category of geometric integrators— a very active area of research during the last few years. The essence of geometric integration is to construct numerical methods that respect underlying constraints, for instance, the configuration space * Corresponding author.
    [Show full text]
  • Teaching Strategies for Improving Algebra Knowledge in Middle and High School Students
    EDUCATOR’S PRACTICE GUIDE A set of recommendations to address challenges in classrooms and schools WHAT WORKS CLEARINGHOUSE™ Teaching Strategies for Improving Algebra Knowledge in Middle and High School Students NCEE 2015-4010 U.S. DEPARTMENT OF EDUCATION About this practice guide The Institute of Education Sciences (IES) publishes practice guides in education to provide edu- cators with the best available evidence and expertise on current challenges in education. The What Works Clearinghouse (WWC) develops practice guides in conjunction with an expert panel, combining the panel’s expertise with the findings of existing rigorous research to produce spe- cific recommendations for addressing these challenges. The WWC and the panel rate the strength of the research evidence supporting each of their recommendations. See Appendix A for a full description of practice guides. The goal of this practice guide is to offer educators specific, evidence-based recommendations that address the challenges of teaching algebra to students in grades 6 through 12. This guide synthesizes the best available research and shares practices that are supported by evidence. It is intended to be practical and easy for teachers to use. The guide includes many examples in each recommendation to demonstrate the concepts discussed. Practice guides published by IES are available on the What Works Clearinghouse website at http://whatworks.ed.gov. How to use this guide This guide provides educators with instructional recommendations that can be implemented in conjunction with existing standards or curricula and does not recommend a particular curriculum. Teachers can use the guide when planning instruction to prepare students for future mathemat- ics and post-secondary success.
    [Show full text]
  • Step-By-Step Solution Possibilities in Different Computer Algebra Systems
    Step-by-Step Solution Possibilities in Different Computer Algebra Systems Eno Tõnisson University of Tartu Estonia E-mail: [email protected] Introduction The aim of my research is to compare different computer algebra systems, and specifically to find out how the students could solve problems step-by-step using different computer algebra systems. The present paper provides the preliminary comparison of some aspects related to step-by-step solution in DERIVE, Maple, Mathematica, and MuPAD. The paper begins with examples of one-step solutions of equations. This is followed by a cursory survey of useful commands, entering commands, programming etc. I hope that a more detailed and complete review will be composed quite soon. Suggestions for complementing the comparison are welcome. It is necessary to know which concrete versions are under consideration. In alphabetical order: DERIVE for Windows. Version 4.11 (1996) Maple V Release 5. Student Version 5.00 (1998) Mathematica for Students. Version 3.0 (1996) MuPAD Light. Version 1.4.1 (1998) Only pure systems (without additional packages, etc.) are under consideration. I believe that there may be more (especially interface-sensitive) possibilities in MuPAD Pro than in MuPAD Light. My paper is not the first comparison, of course. I found several previous ones in the Internet. For example, 1. Michael Wester. A review of CAS mathematical capabilities. 1995 There are 131 short problems covering a broad range of symbolic mathematics. http://math.unm.edu/~wester/cas/Paper.ps (One of the profoundest comparisons is probably M. Wester's book Practical Guide to Computer Algebra Systems.) 1 2.
    [Show full text]
  • The Evolution of Equation-Solving: Linear, Quadratic, and Cubic
    California State University, San Bernardino CSUSB ScholarWorks Theses Digitization Project John M. Pfau Library 2006 The evolution of equation-solving: Linear, quadratic, and cubic Annabelle Louise Porter Follow this and additional works at: https://scholarworks.lib.csusb.edu/etd-project Part of the Mathematics Commons Recommended Citation Porter, Annabelle Louise, "The evolution of equation-solving: Linear, quadratic, and cubic" (2006). Theses Digitization Project. 3069. https://scholarworks.lib.csusb.edu/etd-project/3069 This Thesis is brought to you for free and open access by the John M. Pfau Library at CSUSB ScholarWorks. It has been accepted for inclusion in Theses Digitization Project by an authorized administrator of CSUSB ScholarWorks. For more information, please contact [email protected]. THE EVOLUTION OF EQUATION-SOLVING LINEAR, QUADRATIC, AND CUBIC A Project Presented to the Faculty of California State University, San Bernardino In Partial Fulfillment of the Requirements for the Degre Master of Arts in Teaching: Mathematics by Annabelle Louise Porter June 2006 THE EVOLUTION OF EQUATION-SOLVING: LINEAR, QUADRATIC, AND CUBIC A Project Presented to the Faculty of California State University, San Bernardino by Annabelle Louise Porter June 2006 Approved by: Shawnee McMurran, Committee Chair Date Laura Wallace, Committee Member , (Committee Member Peter Williams, Chair Davida Fischman Department of Mathematics MAT Coordinator Department of Mathematics ABSTRACT Algebra and algebraic thinking have been cornerstones of problem solving in many different cultures over time. Since ancient times, algebra has been used and developed in cultures around the world, and has undergone quite a bit of transformation. This paper is intended as a professional developmental tool to help secondary algebra teachers understand the concepts underlying the algorithms we use, how these algorithms developed, and why they work.
    [Show full text]
  • Constructing a Computer Algebra System Capable of Generating Pedagogical Step-By-Step Solutions
    DEGREE PROJECT IN COMPUTER SCIENCE AND ENGINEERING, SECOND CYCLE, 30 CREDITS STOCKHOLM, SWEDEN 2016 Constructing a Computer Algebra System Capable of Generating Pedagogical Step-by-Step Solutions DMITRIJ LIOUBARTSEV KTH ROYAL INSTITUTE OF TECHNOLOGY SCHOOL OF COMPUTER SCIENCE AND COMMUNICATION Constructing a Computer Algebra System Capable of Generating Pedagogical Step-by-Step Solutions DMITRIJ LIOUBARTSEV Examenrapport vid NADA Handledare: Mårten Björkman Examinator: Olof Bälter Abstract For the problem of producing pedagogical step-by-step so- lutions to mathematical problems in education, standard methods and algorithms used in construction of computer algebra systems are often not suitable. A method of us- ing rules to manipulate mathematical expressions in small steps is suggested and implemented. The problem of creat- ing a step-by-step solution by choosing which rule to apply and when to do it is redefined as a graph search problem and variations of the A* algorithm are used to solve it. It is all put together into one prototype solver that was evalu- ated in a study. The study was a questionnaire distributed among high school students. The results showed that while the solutions were not as good as human-made ones, they were competent. Further improvements of the method are suggested that would probably lead to better solutions. Referat Konstruktion av ett datoralgebrasystem kapabelt att generera pedagogiska steg-för-steg-lösningar För problemet att producera pedagogiska steg-för-steg lös- ningar till matematiska problem inom utbildning, är vanli- ga metoder och algoritmer som används i konstruktion av datoralgebrasystem ofta inte lämpliga. En metod som an- vänder regler för att manipulera matematiska uttryck i små steg föreslås och implementeras.
    [Show full text]
  • Analytic Geometry
    CHAPTER 2 Analytic Geometry Euclid talks about geometry in Elements as if there is only one geometry. Today, some people think of there being several, and others think of there being infinitely many. Hopefully, after you get through this course, you will be in the second group. The people in the first group generally think of geometry as running from Euclid to Hilbert and then branching into Euclidean geometry, hyperbolic geometry and elliptic geometry. People in the second group understand that perfectly well, but include another, earlier brach starting with Rene Descartes (usually pronounced like “day KART”). This branch continues through people like Gauss and Riemann, and even people like Albert Einstein. In my mind, two of the major advances in the understanding of geometry were known to Descartes. One of these, was only known to Descartes, but Gauss, it seems, figured it out on his own, and we all followed him. The other you know very well, but you probably don’t know much about where it came from. This was the development of analytic geometry, geometry using coordinates. The other is not known very well at all, but Descartes noticed something that tells us that geometry should be built upon a general concept of curvature. What is generally called Modern geometry begins with Euclid and ends with Hilbert. The alternate path, the truly contemporary geometry, begins with Descartes and blossoms with Riemann. Note that, as is typical, modern usually means a long time ago. We’ll look at analytic geometry first, and Descartes’ other piece of insight will come later.
    [Show full text]
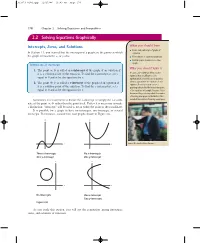
  • 2.2 Solving Equations Graphically
    333371_0202.qxp 12/27/06 11:03 AM Page 176 176 Chapter 2 Solving Equations and Inequalities 2.2 Solving Equations Graphically Intercepts, Zeros, and Solutions What you should learn ᭿ Find x- and y-intercepts of graphs of In Section 1.1, you learned that the intercepts of a graph are the points at which equations. the graph intersects the x- or y-axis. ᭿ Find solutions of equations graphically. ᭿ Find the points of intersection of two graphs. Definitions of Intercepts Why you should learn it 1. The point ͑a, 0͒ is called an x-intercept of the graph of an equation if it is a solution point of the equation. To find the x-intercept(s), set y Because some real-life problems involve equations that are difficult to solve equal to 0 and solve the equation for x. algebraically,it is helpful to use a graphing 2. The point ͑0, b͒ is called a y-intercept of the graph of an equation if utility to approximate the solutions of such equations.For instance,you can use a it is a solution point of the equation. To find the y-intercept(s), set x graphing utility to find the intersection point equal to 0 and solve the equation for y. of the equations in Example 7 on page 182 to determine the year during which the number of morning newspapers in the United States Sometimes it is convenient to denote the x-intercept as simply the x-coordi- exceeded the number of evening newspapers. nate of the point ͑a, 0͒ rather than the point itself.
    [Show full text]
  • Week 4: Differential Equations & Linear Algebra Notes
    Christian Parkinson GRE Prep: Diff. Eq. & Lin. Alg. Notes 1 Week 4: Differential Equations & Linear Algebra Notes After calculus, the most common topic on the math subject GRE is linear algebra, foll- wed by differential equations. Since the latter is a more natural continuation of calculus (and since it will take much less time), I cover it first. Differential Equations Definition 1 (Differential Equation). An ordinary differential equation is an equation of the form F (x; y; y0; y00; : : : ; y(n)) = 0 for some function F : Rn+2 ! R where y(k) denotes the kth derivative of y with respect to the independent variable x. The order of the differential equation is equal to the highest order derivative of u which appears; the above equation is nth order (assuming F does actually depend on its last variable). Note, we often replace y with u which can be thought to stand for \unknown." The goal then, is to find the unknown function which satisfies the equation. On the math subject GRE, questions are mostly limited to equations where the highest order derivative of the unknown function can be isolated; that is, equations of the form y(n) = f(x; y0; : : : ; y(n−1)): Many differential equations can be solved by simply recalling facts from calculus. Example 2. Solve the differential equations (a) u0 = u; (b) y00 = −4y: Solution. For (a), we can phrase the differential equation as a question: \What function will remain the same upon differentiating?" We recall from calculus that u(x) = ex is the function which is invariant under differentiation.
    [Show full text]
  • Higher-Order Linear Differential Equations
    Higher-Order Linear Differential Equations Sean Z. Roberson March 29, 2014 In Chapter 2, we examined a linear differential equation of the form y0 + P y = Q, where P and Q were functions of x (or whatever independent variable is used in the context of the problem). The solution was simple to construct by using an integrating factor. In Chapter 4, our focus shifted to higher-order linear differential equations (which I will abbreviate as DE from now on) which took a bit more work to solve. This paper will summarize the methods discussed in this chapter and will show how to apply each method. 1 Reduction of Order To begin, let's say that one (fundamental) solution of a differential equation is given. How can you find the rest? Doing so requires a substitution. In order to find a second solution to a second-order linear DE, assume that this second solution y2 is the product of some unknown function u and the known solution y1. With this assumption, we take derivatives (quite unfortunately, using the product rule multiple times) and substitute into the DE. Afterwards, the equation is now in terms of the unknown function u, but solely in its derivatives. The equation can then be solved by making the substitution w = u0, which reduces into a first-order DE. We illustrate this with an example. Example 1. x 00 Given that y1 = e is a solution to y − y = 0, find another solution. Solution 1. x 0 x 0 x Let us begin by assuming that this second solution has the form y2 = ue .
    [Show full text]
  • Teaching Physics with Computer Algebra Systems
    AC 2009-334: TEACHING PHYSICS WITH COMPUTER ALGEBRA SYSTEMS Radian Belu, Drexel University Alexandru Belu, Case Western Reserve University Page 14.1147.1 Page © American Society for Engineering Education, 2009 Teaching Physics with Computer Algebra Systems Abstract This paper describes some of the merits of using algebra systems in teaching physics courses. Various applications of computer algebra systems to the teaching of physics are given. Physicists started to apply symbolic computation since their appearance and, hence indirectly promoted the development of computer algebra in its contemporary form. It is therefore fitting that physics is once again at the forefront of a new and exciting development: the use of computer algebra in teaching and learning processes. Computer algebra systems provide the ability to manipulate, using a computer, expressions which are symbolic, algebraic and not limited to numerical evaluation. Computer algebra systems can perform many of the mathematical techniques which are part and parcel of a traditional physics course. The successful use of the computer algebra systems does not imply that the mathematical skills are no longer at a premium: such skills are as important as ever. However, computer algebra systems may remove the need for those poorly understood mathematical techniques which are practiced and taught simply because they serve as useful tools. The conceptual and reasoning difficulties that many students have in introductory and advanced physics courses is well-documented by the physics education community about. Those not stemming from students' failure to replace Aristotelean preconceptions with Newtonian ideas often stem from difficulties they have in connecting physical concepts and situations with relevant mathematical formalisms and representations, for example, graphical representations.
    [Show full text]
  • Teaching the Concept of Function: Definition and Problem Solving Areti Panaoura, Paraskevi Michael-Chrysanthou, Andreas Philippou
    Teaching the concept of function: Definition and problem solving Areti Panaoura, Paraskevi Michael-Chrysanthou, Andreas Philippou To cite this version: Areti Panaoura, Paraskevi Michael-Chrysanthou, Andreas Philippou. Teaching the concept of func- tion: Definition and problem solving. CERME 9 - Ninth Congress of the European Societyfor Research in Mathematics Education, Charles University in Prague, Faculty of Education; ERME, Feb 2015, Prague, Czech Republic. pp.440-445. hal-01286927 HAL Id: hal-01286927 https://hal.archives-ouvertes.fr/hal-01286927 Submitted on 11 Mar 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Teaching the concept of function: Definition and problem solving Areti Panaoura1, Paraskevi Michael-Chrysanthou2 and Andreas Philippou2 1 Frederick University, Department of Education, Nicosia, Cyprus, [email protected] 2 University of Cyprus, Department of Education, Nicosia, Cyprus, [email protected], [email protected] The present study investigates students’ abilities to un- subjects, such as physics (Sanchez & Llinares, 2003). In derstand the concept of function. Secondary education fact, the results we present in this paper are a part of students were asked to (i) define the concept of function a large scale cross-sectional study examining the use and present examples of functions, (ii) translate between of different modes of representations in functions at different representations of a function and (iii) solve the secondary school level.
    [Show full text]