Mapping Batter Ability in Baseball Using Spatial Statistics Techniques
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2021 Texas A&M Baseball
2021 TEXAS A&M BASEBALL GAMES 24-26 | GEORGIA | 3/26-28 GAME TIMES: 6:02 / 2:02 / 1:02 P.M. CT | SITE: Olsen Field at Blue Bell Park, Bryan-College Station, Texas Texas A&M Media Relations * www.12thMan.com Baseball Contact: Thomas Dick / E-Mail: [email protected] / C: (512) 784-2153 RESULTS/SCHEDULE TEXAS A&M GEORGIA Date Day Opponent Time (CT) 2/20 SAT XAVIER (DH) S+ L, 6-10 XAVIER (DH) S+ L, 0-2 AGGIES BULLDOGS 2/21 SUN XAVIER S+ W, 15-0 2/23 TUE ABILENE CHRISTIAN S+ L, 5-6 2/24 WED TARLETON STATE S+ (10) W, 8-7 2/26 Fri % vs Baylor Flo W, 12-4 2021 Record 15-8, 0-3 SEC 2021 Record 15-5, 1-2 SEC 2/27 Sat % vs Oklahoma Flo W, 8-1 Ranking - Ranking 12 (CB); 30 (NCBWA) 2/28 Sun % vs Auburn Flo L, 1-6 Streak Lost 4 Streak Won 1 3/2 TUE HOUSTON BAPTIST S+ W, 4-0 Last 5 / Last 10 1-4 / 6-4 Last 5 / Last 10 3-2 / 8-2 3/3 WED INCARNATE WORD S+ W, 6-4 Last Game Mar 23 Last Game Mar 23 3/5 FRI NEW MEXICO STATE S+ W, 4-1 3/6 SAT NEW MEXICO STATE S+ W, 5-0 RICE - L, 1-2 KENNESAW STATE - (10 inn.) W, 3-2 3/7 SUN NEW MEXICO STATE S+ W, 7-1 3/9 TUE A&M-CORPUS CHRISTI S+ W, 7-0 Head Coach Rob Childress (Northwood, ‘90) Head Coach Scott Stricklin (Kent State, ‘95) 3/10 WED PRAIRIE VIEW A&M S+ (7) W, 22-2 Overall 608-317-3 (16th season) Overall 568-354-1 (17th season) 3/12 FRI SAMFORD S+ W, 10-1 at Texas A&M same at Georgia 218-166-1 (8th season) 3/13 SAT SAMFORD (DH) S+ W, 21-4 SUN SAMFORD (DH) S+ W, 5-2 3/16 Tue at Houston E+ W, 9-4 PROBABLE PITCHING MATCHUPS 3/18 Thu * at Florida SEC L, 4-13 • FRIDAY: #37 Dustin Saenz (Sr., LHP, 3-2, 3.07) vs. -

2018 Purdue Baseball
2018 PURDUE BASEBALL P 2012 BIG TEN CHAMPIONS P • PURDUESPORTS.COM • @PURDUEBASEBALL SID Contact Info: Ben Turner // [email protected] // Office: 765-494-3198 // Cell: 217-549-7965 – FEBRUARY (6-1) – – BIG TEN PLAY CONTINUES – 17 ^ vs Western Michigan W 5-1 ^ vs Western Michigan W 5-1 URDUE OILERMAKERS IG EN 18 ^ vs Western Michigan W 10-4 P B (29-16, 13-4 B T ) 23 # vs Saint Louis W 5-2 AT OHIO STATE BUCKEYES (31-16, 11-7 BIG TEN) # vs Incarnate Word W 5-4 (10) 24 # vs #30 Notre Dame L 4-2 3-GAME SERIES • MAY 11-13 • BILL DAVIS STADIUM • COLUMBUS, OHIO 25 # vs #30 Notre Dame W 8-7 Series Opener: Friday, May 11 at 6:30 p.m. ET • BTN Plus on BTN2Go – MARCH (8-9, 3-0 BIG TEN) – Middle Game: Saturday, May 12 at 3 p.m. ET • BTN Plus on BTN2Go 2 + vs Central Michigan W 11-1 Series Finale: Sunday, May 13 at 1 p.m. ET • BTN Plus on BTN2Go 3 + vs Virginia Tech W 12-5 – SERIES HISTORY – 4 + at Stetson L 11-6 All-Time Series: Ohio State leads 146-64-1 • All-Time in Columbus: Ohio State leads 78-25 9 at Tulane L 1-0 10 at Tulane W 12-8 2017: Purdue won 2-of-3 (March 31-April 2 in Columbus) 11 at Tulane L 6-2 First Meeting: Purdue 4, Ohio State 3 (May 1913 in West Lafayette) 13 at Southeastern Louisiana L 4-0 Road team has won the last 8 Purdue-OSU series dating back to 2007 14 at Nicholls State L 4-2 – LIVE COVERAGE – 17 at Saint Louis L 15-1 Video Webcasts: BTN2Go.com & BTN2Go App at Saint Louis L 11-9 Radio: WSHY 104.3 FM & 1410 AM (Games 1 & 3) • Free Online Audio: PurdueSports.com 18 at Saint Louis L 7-3 – PURDUE’S PROBABLE LINEUP – 23 LIPSCOMB L 3-1 LIPSCOMB W 5-2 POS # NAME ..................................... -

F(Error) = Amusement
Academic Forum 33 (2015–16) March, Eleanor. “An Approach to Poetry: “Hombre pequeñito” by Alfonsina Storni”. Connections 3 (2009): 51-55. Moon, Chung-Hee. Trans. by Seong-Kon Kim and Alec Gordon. Woman on the Terrace. Buffalo, New York: White Pine Press, 2007. Peraza-Rugeley, Margarita. “The Art of Seen and Being Seen: the poems of Moon Chung- Hee”. Academic Forum 32 (2014-15): 36-43. Serrano Barquín, Carolina, et al. “Eros, Thánatos y Psique: una complicidad triática”. Ciencia ergo sum 17-3 (2010-2011): 327-332. Teitler, Nathalie. “Rethinking the Female Body: Alfonsina Storni and the Modernista Tradition”. Bulletin of Spanish Studies: Hispanic Studies and Researches on Spain, Portugal and Latin America 79, (2002): 172—192. Biographical Sketch Dr. Margarita Peraza-Rugeley is an Assistant Professor of Spanish in the Department of English, Foreign Languages and Philosophy at Henderson State University. Her scholarly interests center on colonial Latin-American literature from New Spain, specifically the 17th century. Using the case of the Spanish colonies, she explores the birth of national identities in hybrid cultures. Another scholarly interest is the genre of Latin American colonialist narratives by modern-day female authors who situate their plots in the colonial period. In 2013, she published Llámenme «el mexicano»: Los almanaques y otras obras de Carlos de Sigüenza y Góngora (Peter Lang,). She also has published short stories. During the summer of 2013, she spent time in Seoul’s National University and, in summer 2014, in Kyungpook National University, both in South Korea. https://www.facebook.com/StringPoet/ The Best Players in New York Mets History Fred Worth, Ph.D. -

2020 Toronto Blue Jays Interactive Bios Media & Misc
2020 TORONTO BLUE JAYS INTERACTIVE BIOS ADAMS 76 RI LEY CATCHER BIRTHDATE . June 26, 1996 BATS/THROWS . R/R BIOGRAPHIES BIOGRAPHIES OPENING DAY AGE . 23 HEIGHT/WEIGHT . 6-4/235 BIRTHPLACE . Encinitas, CA CONTRACT STATUS . signed thru 2020 RESIDENCE . Encinitas, CA M .L . SERVICE . 0 .000 NON-ROSTER TWITTER . @RileyAdams OPTIONS USED . 0 of 3 PERSONAL: • Riley Keaton Adams. • Went to high school at Canyon Crest Academy in San Diego, CA, where he also played basketball. • Attended the University of San Diego where he slashed .305/.411/.504 across three seasons. • Originally selected by the Chicago Cubs in 37th round of the 2014 draft but did not sign. LAST SEASON LAST SEASON: • Started his campaign with 19 games for Advanced-A Dunedin and posted an .896 OPS while there. • Named a Florida State League Mid-Season All-Star. • Received a promotion to Double-A New Hampshire on May 3. • Batted .258 with 28 extra-base hits in 81 contests for the Fisher Cats. • Threw out 16 of 52 attempted stolen bases while with New Hampshire (30.8%). Bold – career high; Red – league high Year Club and League AVG G AB R H 2B 3B HR RBI BB IBB SO SB CS OBP SLG OPS SF SH HBP H I S T O RY 2017 Vancouver (NWL) .305 52 203 26 62 16 1 3 35 18 0 50 1 1 .374 .438 .812 1 0 5 2018 Dunedin (FSL) .246 99 349 49 86 26 1 4 43 50 2 93 3 0 .352 .361 .713 2 0 8 2019 Dunedin (FSL) .277 19 65 12 18 3 0 3 12 14 0 18 1 0 .434 .462 .896 0 0 4 New Hampshire (EAS) .258 81 287 46 74 15 2 11 39 32 0 105 3 1 .349 .439 .788 0 3 10 Minor Totals .265 251 904 133 240 60 4 21 129 114 2 266 8 2 .363 .410 .773 0 6 27 TRANSACTIONS • Selected by the Toronto Blue Jays in the 3rd round of the 2017 First-Year Player Draft PROFESSIONAL CAREER: RECORDS MINORS: • Joined Class-A (short) Vancouver in 2017 for his first pro season. -

2019 GOPHER BASEBALL UNIVERSITY of MINNESOTA 2019 > SCHEDULE & RESULTS WEEK 2 > DALLAS, TEXAS FEBRUARY College Baseball Classic (Feb
2019 GOPHER BASEBALL UNIVERSITY OF MINNESOTA 2019 > SCHEDULE & RESULTS WEEK 2 > DALLAS, TEXAS FEBRUARY College Baseball Classic (Feb. 15-18) 15 Gonzaga Surprise, Ariz. W 8-5 16 New Mexico Surprise, Ariz. L 11-1 17 Oregon State Surprise, Ariz. L 13-1 18 Gonzaga Surprise, Ariz. L 6-5 DALLAS BAPTIST 22 Dallas Baptist Dallas, Texas 6:30pm >> VS. >> PATRIOTS 23 Dallas Baptist Dallas, Texas 2pm 3-1 (0-0 Missouri Valley) 24 Dallas Baptist Dallas, Texas 1pm MINNESOTA ALL-TIME SERIES: MARCH GOLDEN GOPHERS Minnesota leads 3-1 1 NC State Raleigh, NC 5pm ET 1-3 (0-0 Big Ten) 2 NC State Raleigh, NC 4pm ET LAST MEETING 3 NC State Raleigh, NC 3pm ET W 11-9, March 21, 2009 Seattle Baseball Showcase (March 8-10) Dallas, Texas 8 Oregon State Seattle, Wash. 3pm PT 9 San Diego Seattle, Wash. 11am PT PROBABLE STARTERS 10 Washington Seattle, Wash. 7pm PT POS. NO. NAME YR. B/T 2019 STATISTICS 11 Seattle Seattle, Wash. 11:30am PT C 4 Eli Wilson So. R/R 4 GP-4 GS, .357/.400/.500, 2 2B, 3 RBI, 3 R 15 Long Beach State Long Beach, Calif. 6pm PT 1B 10 Cole McDevitt Jr. R/R 4 GP-4 GS, .286/.333/.357, 1 2B, RBI, 2 R 16 Long Beach State Long Beach, Calif. 2pm PT 2B 18 Riley Smith Sr. R/R 4 GP-4 GS, .143/.250/.143, 1-2 SB 17 Long Beach State Long Beach, Calif. 1pm PT SS 7 Jordan Kozicky R-Jr. R/R 4 GP-4 GS, .077/.250/.077, 1-1 SB, 1 R 19 Pepperdine Malibu, Calif. -

Fort Myers Miracle Will Host the 2016 FSL All-Star Game All-Star Weekend in Fort Myers Set for June 17-19
Fort Myers Miracle will host the 2016 FSL All-Star Game All-Star Weekend in Fort Myers set for June 17-19 FORT MYERS, Fla. (June 25, 2015) - The Fort Myers Miracle are pleased to announce that the 2016 Florida State League All-Star Game will be hosted at the newly renovated Hammond Stadium at the CenturyLink Sports Complex. The 55th All-Star Game in league history will be played for a sixth time in Fort Myers since 1985 and will be put on by the Miracle for a fifth time. A three-day All-Star break will commence on Friday, June 17 and end on Sunday, June 19. The game will be played on Saturday, June 18 at 7:05 p.m. “We are thrilled to show off this state-of-the art facility after the renovations and upgrades that have improved the fan experience the last two seasons,” said Miracle Chief Operating Officer Steve Gliner. “This event will be a great opportunity not just for local fans, but also for guests from around Florida and the United States to come and experience Fort Myers, Hammond Stadium and the beautiful Southwest Florida region.” Hammond Stadium and the CenturyLink Sports Complex underwent a two-phase, $48.5 million dollar renovation that began during the fall of 2013 and was completed prior to Minnesota Twins Spring Training in the spring of 2015. Phase I included a brand new outfield boardwalk to provide 360-degree viewing, four different types of seating options, two full service bars and new concession stands in center field. -

AUCTION ITEMS FSCNY 18 Annual Conference & Exposition May 11
AUCTION ITEMS FSCNY 18th Annual Conference & Exposition May 11, 2010 These items will be available for auction at the Scholarship booth at FSCNY's Conference & Exposition on May 11th. There will be more baseball items added as we get closer to the conference. All proceeds will go to the FSCNY Scholarship Program. Payment can be made by either a check or credit card. Your continued support is greatly appreciated. Sandy Herman Chairman, Scholarship Committee Baseball Robinson Cano Autographed Baseball Bat - Autographed baseball bat of Yankees Robinson Cano. Bucky Dent and Mike Torrez Autographed Framed Photo - A photo of Bucky Dent's homerun over the green monster in 1978, autographed by Bucky Dent and Mike Torrez. Derek Jeter SI Cover/WS Celebration Collage with Plaque - Original 8x10 photo of SI cover with Derek Jeter Sportsman of the year next to original 8x10 photo of Derek Jeter during locker room celebration after World Series win. Derek Jeter Autographed Baseball - Baseball autographed photo of Yankees Derek Jeter. Derek Jeter Autographed 16x20 Framed Photo - Sepia autographed photo of Yankees Derek Jeter tapping the DiMaggio Quote sign that says I want to Thank the Good Lord for Making me a Yankee. It is also signed by the artist. Derek Jeter 20x24 Photo with Dirt from the Stadium (Sliding into 3rd) - Photo of Derek Jeter sliding dirt from the stadium affixed to the photo. Derek Jeter Framed Photo/Ticket/Scorecard Collage (Record Breaking Hit) - This is a photo of Derek Jeter as he set the all time Yankee hit record with framed with a replica of the ticket and scorecard from the game Jerry Koosman, Ed Charles and Jerry Grote Autographed 8x10 Framed Photo - Autographed photo of Jerry Grote, Ed Charles, and Jerry Koosman at the moment the Mets won the 1969 World Series. -

Marketing/Advertising Prices Signage Signage Location Price Outfield Wall Sign
Marketing/Advertising Prices Signage Signage Location Price Outfield Wall Sign . $1,800 Dugout Top Sign (home/visitors) . $2,000 Bullpen Sign . .. $2,000 Pavilion Sponsor . $3,000 Breezeway Sponsorship . $2,500 On Deck Circle Signage (home/visitors) . $2,000 Join the fun and excitement of Kingsport Mets baseball Stadium Restroom Signage (four restrooms) . $1,500 at Hunter Wright Stadium. The Kingsport Mets are Seating Sections (two sections) . $1,500 committed to offering marketing opportunities designed to Stadium Walkway Signage . .$800 enhance your business and fit your budget. Let us create a Breezeway Sign . .. $800 sponsorship package to fit your advertising needs. Breezeway Banner . $600 Entry Wall Sign . .. $800 Kingsport Mets Highlights Lineup Board (includes PA announcement) . $1,000 • In 2017, hosted “School Spirit Night” games for each city of Standings Board (includes PA announcement)........... $1,000 Kingsport elementary school. The night raised funds for each school. Print Advertising • Established the KMets Foundation which helps raise funds Program Price for local non-profits and charities. Back Cover $1,500 · 27% increase in fan attendance since 2013. Inside Front or Inside Back Cover . $1,000 Full Page Ad . .. $800 • Hunter Wright Stadium hosts multiple local high school and Half Page Ad . .. $500 college games and tournaments throughout the year. Scorecard Page . .. $500 • Other events held at stadium include concerts, wedding and Game Notes . .. $1,000 corporate meetings/outings. Roster Insert . .. $1,000 • In 2015, the Kingsport Mets were selected as the Minor League Affiliate of the Year by the New York Mets. Other Print Opportunities Price Pocket Schedule . $1,500 • KMets won the Appalachian League West Division and made Schedule Poster . -

Oklahoma City Dodgers
Oklahoma City Dodgers Game Information Baseball America’s 2018 Bob Freitas Triple-A Organization of the Year Pacific Coast League Affiliate of the Los Angeles Dodgers Chickasaw Bricktown Ballpark | 2 S. Mickey Mantle Drive | Oklahoma City, OK 73104 | Phone: (405) 218-1000 Alex Freedman: (405) 218-2126 | [email protected] | Lisa Johnson: (405) 218-2143 | [email protected] Round Rock Express (13-10) vs. Oklahoma City Dodgers (8-15) Game #24 of 140/Home #13 of 70 (4-8) Pitching Probables: RR-RHP Akeem Bostick (1-0, 8.03) vs. OKC-RHP Michael Bowden (NR, -.--) Tuesday, April 30, 2019 | Chickasaw Bricktown Ballpark | Oklahoma City, Okla. | 7:05 p.m. CT Radio: KGHM AM-1340 The Game, 1340thegame.com, iHeartRadio - Alex Freedman Today’s Game: The OKC Dodgers and Round Rock Express open their four-game series with a 7:05 p.m. game at Chickasaw Bricktown Ballpark. OKC Dodgers Trends Monday night’s series opener was postponed to Wednesday due to rain...The Dodgers seek back-to-back wins for the third time this season and Overall Record ..........................8-15 Home Record..............................4-8 for the first time since April 15-16. Road Record.................... ..........4-7 Current Streak.................... ........W1 Last Game: Monday’s game was postponed due to rain, but on Sunday, Matt Beaty celebrated his 26th birthday by hitting a three-run homer to Current Road Trip............... .............. Last Road Trip..................... .......1-4 help send the Dodgers to a 4-1 win against San Antonio as the Dodgers avoided a road series sweep at Nelson W. Wolff Municipal Stadium. -

POST GAME NOTES for Tuesday, August 23, 2016 LOS ANGELES ANGELS (52-73) Vs
POST GAME NOTES for Tuesday, August 23, 2016 LOS ANGELES ANGELS (52-73) vs. TORONTO BLUE JAYS (71-54) R H E LOB The Game at a Glance LOS ANGELES 2 8 0 6 TORONTO 7 10 0 7 First Pitch ........................... 7: 08pm Last Pitch ............................ 9:46pm WP: Dickey (9-13) LP: Skaggs (1-3) SV: NA Game Time:............................ 2:38 Weather.......................... 24’C/75’F BLUE JAYS NOTES: th Wind ............. SSW 22KM/14MPH Recorded their 29 sellout of the season…Marks the second time this season that Blue Jays’ batters have struck out two times or fewer in a game…Are now 14-9 in Attendance: ........................ 46,696 games following a 1-run loss…Since the All-Star break in 2015, own the highest Rogers Centre Average: ...... 40,987 win % among AL at .607 (119-77)…Have averaged 5.36 runs/game over their last Rogers Centre Total: ...... 2,582,196 Home Record ......................... 37-26 11 games (7-4 record), hitting a home run in 10 of those contests…Return to a Homestand ................................. 1-0 season-best 17 games above .500…Are now .500 (18-18) vs. LHS. vs. LAA (Season) ...................... 1-0 R.A. DICKEY allowed his 27th home run of the season, tying him with Hector vs. LAA (Series) ........................ 1-0 Santiago for the 4th most home runs allowed by an AL pitcher this year…Recorded Vs. RHS/LHS ............. 53-36/18-18 th 1-run ...................................... 14-22 his 12 quality start of the year, Extra Innings ............................. 4-8 RUSSELL MARTIN is batting .469 (15-32) with 13 RBI over his last eight Come From Behind Wins .......... -

May 26, 2011 Eastern Illinois University
Eastern Illinois University The Keep May 2011 5-26-2011 Daily Eastern News: May 26, 2011 Eastern Illinois University Follow this and additional works at: http://thekeep.eiu.edu/den_2011_may Recommended Citation Eastern Illinois University, "Daily Eastern News: May 26, 2011" (2011). May. 5. http://thekeep.eiu.edu/den_2011_may/5 This Article is brought to you for free and open access by the 2011 at The Keep. It has been accepted for inclusion in May by an authorized administrator of The Keep. For more information, please contact [email protected]. "Tell the truth and don't be afraid." Local educators honored Bos resigns, takes job for positive actions at IUPUI Page 3 Page 8 STATE Commission rejects insurance plan. ten to rhe commission members Gov. Quinn precipitates a constitutional crisis, which will be solved in the courts," Health Alliance, Hurnana refuses to listen Rose said. Rose said the commission vot to lawmakers ed against rhe move because they say patients may be affected did nor believe the numbers Gov. By Alex McNamee Quinn presenred and they did not new insurance and new doctors. Editor in Chief think ir was fair. State employees, retirees 1he commission told The News-Ga "They did not believe it was fair would have to find zcne in Champaign Tuesday that new A policy moving a large num to the taXpayers," Rose said. contracts with Blue Cross and Blue ber of state employees and retir By establishing a new program, Rep. Chapin Rose new doctors, insurance Shield and rwo open~llccess plans will ees into a state self-insurance pro Gov. -
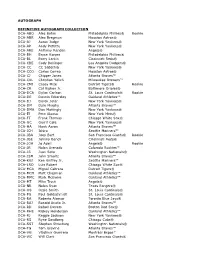
2021 Topps Definitive Collection BB Checklist.Xls
AUTOGRAPH DEFINITIVE AUTOGRAPH COLLECTION DCA-ABO Alec Bohm Philadelphia Phillies® Rookie DCA-ABR Alex Bregman Houston Astros® DCA-AJ Aaron Judge New York Yankees® DCA-AP Andy Pettitte New York Yankees® DCA-ARE Anthony Rendon Angels® DCA-BH Bryce Harper Philadelphia Phillies® DCA-BL Barry Larkin Cincinnati Reds® DCA-CBE Cody Bellinger Los Angeles Dodgers® DCA-CC CC Sabathia New York Yankees® DCA-CCO Carlos Correa Houston Astros® DCA-CJ Chipper Jones Atlanta Braves™ DCA-CKL Christian Yelich Milwaukee Brewers™ DCA-CMI Casey Mize Detroit Tigers® Rookie DCA-CR Cal Ripken Jr. Baltimore Orioles® DCA-DCA Dylan Carlson St. Louis Cardinals® Rookie DCA-DE Dennis Eckersley Oakland Athletics™ DCA-DJ Derek Jeter New York Yankees® DCA-DM Dale Murphy Atlanta Braves™ DCA-DMA Don Mattingly New York Yankees® DCA-EJ Pete Alonso New York Mets® DCA-FT Frank Thomas Chicago White Sox® DCA-GC Gerrit Cole New York Yankees® DCA-HA Hank Aaron Atlanta Braves™ DCA-ICH Ichiro Seattle Mariners™ DCA-JBA Joey Bart San Francisco Giants® Rookie DCA-JBE Johnny Bench Cincinnati Reds® DCA-JOA Jo Adell Angels® Rookie DCA-JR Nolan Arenado Colorado Rockies™ DCA-JS Juan Soto Washington Nationals® DCA-JSM John Smoltz Atlanta Braves™ DCA-KGJ Ken Griffey Jr. Seattle Mariners™ DCA-LRO Luis Robert Chicago White Sox® DCA-MCA Miguel Cabrera Detroit Tigers® DCA-MCH Matt Chapman Oakland Athletics™ DCA-MMC Mark McGwire Oakland Athletics™ DCA-MT Mike Trout Angels® DCA-NR Nolan Ryan Texas Rangers® DCA-OS Ozzie Smith St. Louis Cardinals® DCA-PG Paul Goldschmidt St. Louis Cardinals® DCA-RA Roberto Alomar Toronto Blue Jays® DCA-RAJ Ronald Acuña Jr.