The Dynamic Interaction Between Road Density and Land Uses in West Malaysian Cities
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Director of Importer / Distributor in Malaysia AGRICULTURAL
Director of Importer / Distributor in Malaysia AGRICULTURAL FEEDMILLS ANIMAL HEALTH PRODUCTS Sinmah Multifeed Sdn. Bhd. Agritech Enterprise Sdn. Bhd. AG5730, Alor Gajah Industrial Estate 22, Jalan SS4C/5, Taman Rasa Sayang 78000 Alor Gajah, Melaka 47301 Petaling Jaya Tel: 606-5561293 Tel: 603-78033226, 78035239 Fax: 606-5562445 Fax: 603-78033911 Email : [email protected] Email: [email protected] Website : www.sinmah.com.my Contact: Mr. Chew Heng Chong – M.D. Gymtech Feedmill (Malacca) Sdn. Bhd. Chem Ventures Sdn. Bhd Lot 13A, Kawasan Perindustrian Bukit Rambai 32-3, USJ 1/1C, USJ 1 75250 MELAKA 47620 Subang Jaya Tel: 606-3512992 Tel: 603-80241877 Fax: 606-3512998 Fax: 603-80241868 Email: [email protected] Ayamas Integrated Poultry Industry Sdn. Bhd. Contact: Mr. Quah Siew Seng Feedmill Division Jalan Parang, Pelabuhan Utara 42007 Pelabuhan Klang, SELANGOR QL Pacific Vet Group Sdn. Bhd. Tel: 603-31766954 Bay C8 Lot 886, Jalan Subang 9 Fax: 603-31766946 Taman Industri Sg. Penaga 47500 Subang Jaya KL Supreme Feedmill Sdn. Bhd. Tel: 603-80249508 No. 5, Persiaran Industry, Fax: 603-80249634 Sri Damansara Industry Park Email: [email protected] 52200 KUALA LUMPUR Contact: Mr. Cheah Soon Hai Tel: 03-62736781 Fax: 03-62736591 SCC Corporation Sdn. Bhd. 19-21, Jalan Hujan, Taman Overseas Union Gold Coin Feedmills (M) Sdn. Bhd. 58200 Kuala Lumpur Jalan Parang, Pelabuhan Utara, Tel: 603-77828384 P. O. Box 68 Fax: 603-77818561 42000 Pelabuhan Klang, Selangor Email: [email protected] Tel: 03-31767300, 31767311 Contact: Mr. Goh Keng Chin Fax: 03-31767295, 31766842 Johor Bahru Flour Mills Sdn. -

Ecotank Festive Store Locator (1).Xlsx
EPSON ECOTANK FESTIVE REWARDS PROMOTION - PARTICIPATING DEALERS Region Coverage Area Company Name Address Tel Fax AEON AU2, 1st Floor, (AEON Digital Mall), No. 6, Central AEON Ampang Utara Pineapple Computer Systems Sdn Bhd (AEON) Jalan Taman Setiawangsa (37/56), AU2, Taman Keramat, 54200 Kuala Lumpur 1st Floor, AEON Bandar Baru Klang, 41150 Klang, Central AEON Bandar Baru Klang SNS Network Sdn Bhd Selangor Lower Ground Floor, AEON BIG Mid Valley, 59200 Central AEON Big Mid Valley SNS Network Sdn Bhd Kuala Lumpur Central AEON Big Putrajaya SNS Network Sdn Bhd 1st Floor, AEON BIG Putrajaya, 62000 Putrajaya Central AEON Big Subang SNS Network Sdn Bhd 2nd Floor, AEON Big Subang, 47500 Subang Jaya 2nd Floor, AEON Bukit Mertajam, 14000 Bukit Central AEON Bukit Mertajam SNS Network Sdn Bhd Mertajam, Penang No. 1, Persiaran Batu Nilam 1/KS 6, Bandar Bukit Central AEON Bukit Tinggi Pineapple Computer Systems Sdn Bhd (AEON) Tinggi 2, 41200 Klang, Selangor 1st Floor, AEON Cheras Selatan, 43200 Balakong, Central AEON Cheras Selatan SNS Network Sdn Bhd Selangor, Malaysia Ground Floor, Lot G-40, Batu 9, IOI Mall, Jusco Central AEON IOI Mall Pineapple Computer Systems Sdn Bhd (AEON) Bandar Puchong, Bandar Puchong Jaya, 47200, Puchong Selangor Jusco Metra Prima Store, Lot. No. 4086, Fasa 3B (ii), Central AEON Kepong Pineapple Computer Systems Sdn Bhd (AEON) Jalan Metro Prima/Jalan Kepong, Mukim Batu, 52100, Kuala Lumpur 2nd Floor Mid Valley, AT3, Mid Valley Mega Mall, Central AEON Mid Valley Pineapple Computer Systems Sdn Bhd (AEON) Mid Valley City, 58300, Kuala Lumpur 2nd Floor, Jusco Bandar Utama, No. -

PLUS EXPRESSWAYS BERHAD 13 September 2011 COUNTRY OVERVIEW
THE WORLD, Expansion and Modernization of Road Infrastructure II by PLUS EXPRESSWAYS BERHAD 13 September 2011 COUNTRY OVERVIEW COMPANY OVERVIEW MAJOR PROGRAM/ PROJECT IN THE COUNTRY INDUSTRY CHALLENGES PLUS North-South Expressway, Kuala Lumpur bound 2 Country Overview Land area: 329,847 square kilometres (127,350 sq mi) separated by the South China Sea into two regions, Peninsular Malaysia and Malaysian Borneo (slightly smaller than the size of Germany and slightly bigger than Italy). Land borders: Thailand, Indonesia, and Brunei Population 2010: 27,565,821 (Department of Statistics Malaysia) GDP (PPP) : USD442.01 billion - 2010 est (Source: IMF) GDP per capita : USD8,620 - 2010 est (Source: IMF) 3 GDP Growth 2010: 7.2% Country Overview MALAYSIA GDP GROWTH 2000-2011 (est) POPULATION IN MALAYSIA 10.0% 8.3% 30.0 27.1 27.6 7.1% 7.2% 25.0 8.0% 6.3% 5.3% 25.0 22.3 5.2% 6.0% 4.2% 4.6% 19.6 20.0 17.2 5.9% 15.0 4.0% 5.0% 13.2 15.0 11.7 2.0% 10.3 Million 10.0 GDPGrowth 0.0% 0.4% 5.0 -2.0% -1.7% 0.0 -4.0% NEW VEHICLES REGISTERED IN MALAYSIA NUMBER OF TOURIST ARRIVALS IN MALAYSIA 30.0 600 552 548 523 23.6 491 503 25.0 20.9 435 488 487 500 24.6 396 406 20.0 22.0 400 343 15.7 15.0 13.2 17.4 300 16.4 Million 200 10.0 12.7 10.2 10.5 Thousand Vehicles Thousand 100 5.0 0 0.0 COUNTRY OVERVIEW COMPANY OVERVIEW MAJOR PROGRAM/ PROJECT IN THE COUNTRY INDUSTRY CHALLENGES Persada PLUS, Corporate Office 5 Primary toll road operator in Malaysia As at 12 May 2011 # 15.5% 100% r 38.5% Domestic 100% 100% 100% 100% 100% 100% 20% Projek Lebuhraya Expressway Linkedua -

Chapter 6 Existing Environment
ENVIRONMENTAL IMPACT ASSESSMENT (EIA) October 2019 Proposed Development of Sustainable Scheduled Waste Treatment Center (SSWTC) at PT1682 Bukit Tagar Sanitary Landfill, Mukim Sungai Tinggi, Daerah Hulu Selangor, Selangor Darul Ehsan for Berjaya Alam Murni Sdn. Bhd. CHAPTER 6 EXISTING ENVIRONMENT 6.0 Introduction This chapter outlines the existing environment concerning the physical environment, land use pattern, socio-economic characteristics and human health conditions in vicinity of the existing Proposed Project site. The information serves as the background or baseline data on various aspects of subject matters in connection with the proposed scheduled waste management facilities. The existing environmental baseline is obtained from primary and secondary sources. Field investigations were carried out to supplement any insufficient of information for the study area. The condition of the existing environment of the project site and within five (5) km radius of surrounding area is further described in this chapter. The compiled data on the existing environment is regarded as ‘baseline’ environmental condition to assess potential environmental changes, if any that may arise during the implementation of SSWTC project. The discussion on existing environment will be based on the physical environment, human environment and baseline environmental quality at the surrounding area of the project site. Information provided on this chapter was gathered through primary and secondary information including site observations and monitoring, socio- economic and health assessment survey, desktop data search, abstraction of information from published reports and related agencies. 6.1 Zone of Study The zone of study is within five (5) km radius from the Proposed Project site called as the Zone of Impact (ZOI). -

Assessment of Potential Risk Factors and Skin Ultrasound Presentation Associated with Breast Cancer-Related Lymphedema in Long-Term Breast Cancer Survivors
diagnostics Article Assessment of Potential Risk Factors and Skin Ultrasound Presentation Associated with Breast Cancer-Related Lymphedema in Long-Term Breast Cancer Survivors Khairunnisa’ Md Yusof 1,2,3, Kelly A. Avery-Kiejda 2,3, Shafinah Ahmad Suhaimi 4 , Najwa Ahmad Zamri 4, Muhammad Ehsan Fitri Rusli 4 , Rozi Mahmud 5,6, Suraini Mohd Saini 5,6, Shahad Abdul Wahhab Ibraheem 6, Maha Abdullah 4,7,* and Rozita Rosli 4,* 1 Department of Biomedical Sciences, Faculty of Medicine and Health Sciences, Universiti Putra Malaysia, Serdang, Selangor 43400, Malaysia; [email protected] 2 Hunter Medical Research Institute, New Lambton Heights, NSW 2305, Australia; [email protected] 3 School of Biomedical Sciences and Pharmacy, College of Medicine, Health and Wellbeing, The University of Newcastle, Newcastle, NSW 2308, Australia 4 UPM-MAKNA Cancer Research Laboratory, Institute of Bioscience, Universiti Putra Malaysia, Selangor 43400, Malaysia; [email protected] (S.A.S.); [email protected] (N.A.Z.); [email protected] (M.E.F.R.) 5 Centre for Diagnostic Nuclear Imaging, Universiti Putra Malaysia, Selangor 43400, Malaysia; [email protected] (R.M.); [email protected] (S.M.S.) 6 Citation: Yusof, K.M.; Avery-Kiejda, Department of Radiology, Faculty of Medicine and Health Sciences, Universiti Putra Malaysia, Selangor 43400, Malaysia; [email protected] K.A.; Ahmad Suhaimi, S.; Ahmad 7 Department of Pathology, Faculty of Medicine and Health Sciences, Universiti Putra Malaysia, Zamri, N.; Rusli, M.E.F.; Mahmud, R.; Selangor 43400, Malaysia Saini, S.M.; Abdul Wahhab Ibraheem, * Correspondence: [email protected] (M.A.); [email protected] (R.R.) S.; Abdullah, M.; Rosli, R. -

Report 2019/2020
2020 The Educational, Welfare & Research Foundation Malaysia Yayasan Pelajaran, Kebajikan & Penyelidikan Malaysia PPM-001-14-02011979 ANNUAL REPORT 2019/2020 OUR SOCIETY OUR RESPONSIBILITY EWRF BRANCHES THROUGHOUT MALAYSIA IPOH SG. PETANI PENANG AYER TAWAR NO. 48 A, PERSIARAN NO. 313, 2ND FLOOR JALAN S. PANNIIRSELVAN M. SANTHA DEVI BUNTONG JAYA 4, CINTA SAYANG, 08000 SUNGAI 017- 478 8077 012- 585 3810 TAMAN BUNTONG JAYA, PETANI, KEDAH. SG. SIPUT 30100 IPOH, PERAK. J. JEEVABALAN 012- 569 7551 NO. 478 B, TINGKAT 3, S. GOPI ANNUAL REPORT JALAN IPOH, TAMAN HEAWOOD, 017- 527 2895 31100 SUNGAI SIPUT, PERAK. S. MAHENDRAN 016- 555 3947 TELUK INTAN NO. 1691, JALAN INTAN 3, BANDAR BARU, GOMBAK 36000 TELUK INTAN, S. SUNDARA MURTHI PERAK. 012- 348 0894 A. DURAI RAJ 013- 523 1587 HULU SELANGOR NO. 3, JALAN KEMBOJA 18/1 TANJONG MALIM SEKSYEN BB4, NO. 22, TINGKAT 1 & 2, BUKIT BERUNTUNG, JALAN CAHAYA, 48300 RAWANG, TAMAN ANGERIK DESA, SELANGOR. 35900 TANJONG MALIM, R. SUBATHIRAH PERAK. 019- 289 2489 K. KUMARESU 012- 207 3312 RAWANG EWRF HEADQUARTERS NO. 37, JALAN 8, NO. 4B, PERSIARAN ZAABA, TAMAN BUKIT RAWANG PUTRA, 48000 RAWANG, TAMAN TUN DR. ISMAIL, 60000 KUALA LUMPUR. SELANGOR. 2019/2020 R. MURUGAN 1-800-88-3973 012- 606 2617 SUBANG JAYA NO. 42-2F, JALAN USJ 9/5Q, JOHOR BAHRU 47620 SUBANG JAYA, SELANGOR. NO. 6054 - A, JALAN SIANTAN 1, BANDAR INDAH PUTRA, S. KANNAH 81000 KULAI JOHOR. 017- 876 7506 K. RAAM KUMAR KAJANG 017- 763 3134 NO. 10, JALAN KAJANG MEWAH 1, TAMAN KAJANG MEWAH, 43000 KAJANG, SELANGOR. G. ELANGOVAN 012- 671 3045 AMPANG KLUANG NO. -

Factors Behind the Changes in Small Towns Along the Selangor Northern
International Journal of Academic Research in Business and Social Sciences Vol. 9 , No. 2, Feb, 2019, E-ISSN: 2222 -6990 © 2019 HRMARS Factors Behind the Changes in Small Towns along the Selangor Northern Corridor Resulting from Spillover of The Klang-Langat Valley Metropolitan Region: A Confirmatory Factor Analysis Approach (CFA) Y. Saleh, H. Mahat, M. Hashim, N. Nayan & S.B. Norkhaidi To Link this Article: http://dx.doi.org/10.6007/IJARBSS/v9-i2/5531 DOI: 10.6007/IJARBSS/v9-i2/5531 Received: 07 Jan 2019, Revised: 24 Feb 2019, Accepted: 06 March 2019 Published Online: 07 March 2019 In-Text Citation: (Saleh, Mahat, Hashim, Nayan, & Norkhaidi, 2019) To Cite this Article: Saleh, Y., Mahat, H., Hashim, M., Nayan, N., & Norkhaidi, S. B. (2019). Factors Behind the Changes in Small Towns along the Selangor Northern Corridor Resulting from Spillover of The Klang-Langat Valley Metropolitan Region: A Confirmatory Factor Analysis Approach (CFA). International Journal of Academic Research in Business and Social Sciences, 9(2), 159–174. Copyright: © 2019 The Author(s) Published by Human Resource Management Academic Research Society (www.hrmars.com) This article is published under the Creative Commons Attribution (CC BY 4.0) license. Anyone may reproduce, distribute, translate and create derivative works of this article (for both commercial and non-commercial purposes), subject to full attribution to the original publication and authors. The full terms of this license may be seen at: http://creativecommons.org/licences/by/4.0/legalcode Vol. 9, No. 2, 2019, Pg. 159 - 174 http://hrmars.com/index.php/pages/detail/IJARBSS JOURNAL HOMEPAGE Full Terms & Conditions of access and use can be found at http://hrmars.com/index.php/pages/detail/publication-ethics 159 International Journal of Academic Research in Business and Social Sciences Vol. -

1 1.0 INTRODUCTION Waste Has Been a Perennial Source Of
1.0 INTRODUCTION Waste has been a perennial source of pollution ever since the industrial activities generated enormous quantum of complex by-products. Proper waste management is very crucial to prevent further destruction to the ecosystem. It requires appropriate management facilities together with necessary laws and regulations. However the lack of awareness, facilities, technologies and most of all, sufficient funding made it unworkable (Zotos et al., 2009; Fauziah et al., 2004). These factors constrain Malaysia as a fast developing country in the Asian region to establish an effective waste management system (Chowdhury, 2009). Consecutive sections discuss current waste management practise in Malaysia and the need for its improvement. 1.1 Waste Management in Malaysia Malaysia with a total land area of 328 550 km2 produced approximately 30,000 tonnes/day of waste in 2009 (or 1.3 kg/capita/day) up from 18,000 tonnes in 2004 (Agamuthu et al., 2009; Agamuthu et al., 2004). In Malaysia, municipal solid waste (MSW) consists of domestic and industrial refuse, slightly differs to that of United State where MSW is garbage or trash in USEPA classification. Daily MSW volume in Kuala Lumpur was 99 tonnes in 1970s, but had increased rapidly to 587 tonnes in 1990s while to date it has exceeded 3200 tonnes (Latifah et al., 2009; Agamuthu et al., 2009). Similar increases are experienced by other states that it caused alarming situation particularly on the treatment and disposal options (Chong, 2003; News Strait Times, 2006). It was due to 1 the fast development in residential and industrial sectors, as well as, the mushrooming of urban areas. -

Information Is Updated As at 27 July 2017 Page 1 of 4 ATTACHMENT
ATTACHMENT/LAMPIRAN VENTASERV VENDING MACHINES LOCATIONS No Company's Name Address Level 9, Customer Service Centre, Tower A, Vertical Business Suite, Avenue 3, Bangsar 1 CTOS Data Systems Sdn Bhd South, No.8, Jalan Kerinchi, 59200 KL C-G-15, Block C, Jalan Dataran SD1, PJU 9 Bandar Sri Damansara, 52000 Kuala Lumpur 2 GHL Systems Sdn Bhd (Grd Floor) 17th Floor, Menara CIMB, Jalan Stesen Sentral 2, Kuala Lumpur Sentral, 50470 Kuala 3 CIMB - KL Sentral Lumpur (Level 2) 17th Floor, Menara CIMB, Jalan Stesen Sentral 2, Kuala Lumpur Sentral, 50470 Kuala 4 CIMB - KL Sentral Lumpur (Grd Floor) 5 ParkCity Club Management Bhd The ParkCity Club, No 7 Persiaran Residen, Desa ParkCity, 52200 KL.(Sports Field) 6 ParkCity Club Management Bhd The ParkCity Club, No 7 Persiaran Residen, Desa ParkCity, 52200 KL.(Gym) 7 ParkCity Club Management Bhd The ParkCity Club, No 7 Persiaran Residen, Desa ParkCity, 52200 KL.(Gym) FF-27, The Waterfront @ ParkCity ,No. 5, Persiaran Residen, Desa Park City, 52200 8 Renown Point Sdn Bhd KL.(Taxi Stand #2) 9 QHC Medical Center No.2, Jalan USJ 9/5R, 47620 UEP Subang Jaya, Selangor Darul Ehsan. 10 ParkCity Club Management Bhd The ParkCity Club, No 7 Persiaran Residen, Desa ParkCity, 52200 KL.(Gym-Tennis) Jalan Kontraktor U1/14, Hicom-Glenmarie Industrial Park, 40150 Shah Alam, Selangor. 11 Paramount Property Development (Food Court) 12 Porite (M) Sdn Bhd Jalan Keluli 1, Sek 7, Kawasan Perindustrian 40000 Shah Alam, Selangor Lot 137, No 1, Jalan Jasmin, Kawasan Perindustrian Bukit Beruntung, 48300 Bukit 13 Riverstone (M) Sdn Bhd Beruntung, Selangor. -
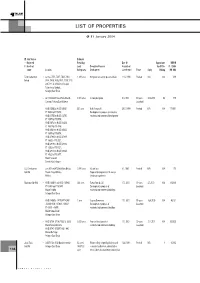
List of Properties
LIST OF PROPERTIES @ 31 January 2004 @ Joint Venture Estimated + Registered Remaining Date Of Approximate NBV @ # Beneficial Land/ Description/Proposed Acquisition / Age Of The 31.1.2004 owner Location Built up area Development Joint Venture Tenure Expiry Building RM ‘000 Talam Corporation + Lot nos. 7073, 7207, 7208, 7410, 1.635 acres Bungalow lots sold on piecemeal basis 11.12.1986 Freehold N/A N/A 698 Berhad 7424, 7425, 7426, 7427, 7209, 7210 and 7211 all in Mukim of Setapak Talam Setia, Gombak, Selangor Darul Ehsan + Lot 174 Mukim Tanah Rata, Daerah 2.401 acres 2-storey bungalow 5.4.1972 60 years 23.4.2033 62 775 Cameron, Pahang Darul Makmur Leasehold + HS(D) 30066 to H.S(D) 30361 561 acres Bukit Sentosa III 29.10.1994 Freehold N/A N/A 174,951 PT 15683 to PT15978; Development in progress for industrial, HS(D) 33755 to H.S(D) 34750 residential and commercial development PT 15979 to PT16974; HS(D) 34751 to H.S(D) 35606 PT 16979 to PT17834; HS(D) 35619 to H.S(D) 35622 PT 16975 to PT16978; HS(D) 27836 to H.S(D) 27935 PT 13822 to PT13921; HS(D) 28193 to H.S(D) 29092 PT 13922 to PT14821; HS(D) 29189 to H.S(D) 30044 PT 14822 to PT15677. Mukim Serendah Daerah Hulu Selangor G.L. Development + Lots 875 and 876 Bukit Baru Melaka 0.355 acres Vacant land 9.1.1982 Freehold N/A N/A 179 Sdn Bhd Daerah Tengah Melaka Proposed development of 16 units of Melaka 3-bedroom apartments Maxisegar Sdn Bhd + HS(D) 146408 and HS(D) 145840, 324 acres Taman Puncak Jalil 17.1.2001 99 years 2.7.2100 N/A 314,986 PT 51440 and PT 51439 Development in progress of Leasehold -

Citf | Pengumuman Mengenai Inisiatif Vaksinasi Secara Walk-In Di Lembah
PASUKAN PETUGAS KHAS IMUNISASI COVID-19 COVID-19 IMMUNISATION TASK FORCE (CITF) PENGUMUMAN MENGENAI INISIATIF VAKSINASI SECARA WALK-IN DI LEMBAH KLANG SELEPAS 22 OGOS 2021 Lanjutan daripada kejayaan Operasi Lonjakan Kapasiti baru-baru ini, Petugas Khas Imunisasi COVID-19 (CITF) ingin memaklumkan beberapa ketetapan baharu yang dibuat sebagai kesinambungan kepada usaha pemvaksinan di Lembah Klang dan setelah mengambil kira perancangan operasi PPV sebelum ini serta keperluan semasa berdasarkan data yang dikumpul semenjak Operasi ini dilaksanakan. 1. CITF mendapati bilangan walk-in untuk warganegara Malaysia telah semakin berkurangan dari hari ke hari semenjak walk-in dimulakan pada 2 Ogos yang lalu. Oleh itu, walk-in untuk semua warganegara Malaysia di Lembah Klang akan diteruskan tetapi di 13 Pusat Pemberian Vaksin (PPV) tertentu seperti di Lampiran 1. 2. Bagi bukan warganegara Malaysia di Lembah Klang, kaedah walk-in yang dikhususkan di Pusat Pemberian Vaksin Stadium Nasional Bukit Jalil (PPV SNBJ) sehingga 22 Ogos akan digantikan dengan vaksinasi melalui kaedah janji temu. Ini bermakna, PPV SNBJ tidak lagi menerima walk-in bukan warganegara bermula 23 Ogos ini. Langkah ini diambil agar proses pemvaksinan bukan warganegara, yang menyaksikan sambutan yang amat baik selama tempoh ia dilaksanakan baru-baru ini, dapat berjalan dalam keadaan yang lebih selamat dan selesa lagi. Bukan warganegara yang masih belum mendaftar untuk PICK perlu berbuat demikian sama ada melalui MySejahtera, talian PICK di 1800-888-828 atau laman web www.vaksincovid.gov.my agar janji temu dapat diberikan. Setiap warganegara yang walk-in ke PPV seperti yang disenaraikan di Lampiran 1 dan bukan warganegara yang pergi ke PPV mengikut janji temu perlu membuktikan bahawa mereka adalah pemastautin di Lembah Klang, dengan membawa surat atau dokumen yang berkenaan seperti kad kerja, bil utiliti atau sebarang dokumen lain yang berkaitan. -

Senarai Fasiliti Swasta Yang Boleh Menjalankan Saringan Covid-19 Di
SENARAI FASILITI SWASTA YANG BOLEH MENJALANKAN SARINGAN COVID-19 DI DALAM KAWASAN PREMIS (A) SENARAI KLINIK PERUBATAN SWASTA BERDAFTAR YANG BOLEH MENJALANKAN SARINGAN COVID-19 DI DALAM KAWASAN PREMIS SEHINGGA 30 NOVEMBER 2020 BIL. NAMA KLINIK ALAMAT KLINIK JENIS UJIAN TARIKH MULA JOHOR 1. KLINIK LEE DAN 45 (GROUND FLOOR), JALAN MUTIARA 1/2, TAMAN MUTIARA MAS, JALAN RT-PCR 16 APRIL 2020 SURGERI GELANG PATAH-SKUDAI, 81300 SKUDAI, JOHOR 2. KLINIK CENTRAL 24 92 GROUND FLOOR, JALAN ADDA 7, TAMAN ADDA, 81100 JOHOR BAHRU RT-PCR 13 MEI 2020 JAM 3. KLINIK MEDIVIRON NO 87, JALAN INDAH 15/2, TAMAN BUKIT INDAH, 81200 JOHOR BAHRU, RT-PCR 18 MEI 2020 BUKIT INDAH JB JOHOR 4. KLINIK RELY ON NO 1-01, GROUND FLOOR, JALAN SEMARAK 1, TAMAN DESARU UTAMA, RT-PCR 22 MEI 2020 BESTARI 81930 BANDAR PENAWAR, JOHOR 5. KLINIK YAP & (GROUND FLOOR), 7523 & 7524, JALAN ENGGANG 19, BANDAR PUTRA, 81000 RT-PCR 28 MEI 2020 PARTNERS KULAI, JOHOR 6. KLINIK ANGKASA TINGKAT BAWAH, NO 147, JALAN SCIENTEX JAYA 7, TAMAN SCIENTEX, RT-PCR 28 MEI 2020 81400 SENAI, JOHOR 7. MJ HEALTHCARE P-01-14 (TINGKAT BAWAH), TELUK AKUA BIRU, JALAN FOREST CITY 3, RT-PCR 29 MEI 2020 CLINIC PULAU SATU, 81550 GELANG PATAH, JOHOR 8. POLIKLINIK NO. 104, JALAN BINTANG, TAMAN BINTANG 81400 SENAI, JOHOR RT-PCR 29 MEI 2020 PENAWAR 9. POLIKLINIK NO. 16, PUSAT BANDAR, BANDAR PENAWAR, 81900 KOTA TINGGI, JOHOR RT-PCR 10 JUN 2020 PENAWAR 10. POLIKLINIK NO. 31 & 32, JALAN PADI RIA, BANDAR BARU UDA 81200 TAMPOI, JOHOR RT-PCR 10 JUN 2020 PENAWAR BANDAR BARU UDA 11.