Experimental Fracture Mechanics Through Digital Image Analysis Alireza Mehdi-Soozani Iowa State University
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Meat: a Novel
University of New Hampshire University of New Hampshire Scholars' Repository Faculty Publications 2019 Meat: A Novel Sergey Belyaev Boris Pilnyak Ronald D. LeBlanc University of New Hampshire, [email protected] Follow this and additional works at: https://scholars.unh.edu/faculty_pubs Recommended Citation Belyaev, Sergey; Pilnyak, Boris; and LeBlanc, Ronald D., "Meat: A Novel" (2019). Faculty Publications. 650. https://scholars.unh.edu/faculty_pubs/650 This Book is brought to you for free and open access by University of New Hampshire Scholars' Repository. It has been accepted for inclusion in Faculty Publications by an authorized administrator of University of New Hampshire Scholars' Repository. For more information, please contact [email protected]. Sergey Belyaev and Boris Pilnyak Meat: A Novel Translated by Ronald D. LeBlanc Table of Contents Acknowledgments . III Note on Translation & Transliteration . IV Meat: A Novel: Text and Context . V Meat: A Novel: Part I . 1 Meat: A Novel: Part II . 56 Meat: A Novel: Part III . 98 Memorandum from the Authors . 157 II Acknowledgments I wish to thank the several friends and colleagues who provided me with assistance, advice, and support during the course of my work on this translation project, especially those who helped me to identify some of the exotic culinary items that are mentioned in the opening section of Part I. They include Lynn Visson, Darra Goldstein, Joyce Toomre, and Viktor Konstantinovich Lanchikov. Valuable translation help with tricky grammatical constructions and idiomatic expressions was provided by Dwight and Liya Roesch, both while they were in Moscow serving as interpreters for the State Department and since their return stateside. -

Faults and Joints
133 JOINTS Joints (also termed extensional fractures) are planes of separation on which no or undetectable shear displacement has taken place. The two walls of the resulting tiny opening typically remain in tight (matching) contact. Joints may result from regional tectonics (i.e. the compressive stresses in front of a mountain belt), folding (due to curvature of bedding), faulting, or internal stress release during uplift or cooling. They often form under high fluid pressure (i.e. low effective stress), perpendicular to the smallest principal stress. The aperture of a joint is the space between its two walls measured perpendicularly to the mean plane. Apertures can be open (resulting in permeability enhancement) or occluded by mineral cement (resulting in permeability reduction). A joint with a large aperture (> few mm) is a fissure. The mechanical layer thickness of the deforming rock controls joint growth. If present in sufficient number, open joints may provide adequate porosity and permeability such that an otherwise impermeable rock may become a productive fractured reservoir. In quarrying, the largest block size depends on joint frequency; abundant fractures are desirable for quarrying crushed rock and gravel. Joint sets and systems Joints are ubiquitous features of rock exposures and often form families of straight to curviplanar fractures typically perpendicular to the layer boundaries in sedimentary rocks. A set is a group of joints with similar orientation and morphology. Several sets usually occur at the same place with no apparent interaction, giving exposures a blocky or fragmented appearance. Two or more sets of joints present together in an exposure compose a joint system. -

Crack Growth During Brittle Fracture in Compres1
CRACK GROWTH DURING BRITTLE FRACTURE IN COMPRES1 by -SIST. TEC, L I SRA' BARTLETT W. PAULDING, JR. LIN DGRE~N Geol. Eng., Colorado School of Mines (1959) SUBMITTED IN PARTIAL, FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY at the MASSACHjUSETTS INSTITUTE OF TECHNOLOGY June 1965 Signature of Author Departmenit of Geology an4'Geophysics, February 9, 1965 Certified by.......... Thesis Supervisor- Accepted by .... Chairman, Departmental Committee on Graduate Students Room 14-0551 77 Massachusetts Avenue Cambridge, MA 02139 Ph: 617.253.5668 Fax: 617.253.1690 MITLibraries Email: [email protected] Document Services http,//Iibraries.mit.,edu/doos DISCLAIMER OF QUALITY Due to the condition of the original material, there are unavoidable flaws in this reproduction. We have made every effort possible to provide you with the best copy available. If you are dissatisfied with this product and find it unusable, please contact Document Services as soon as possible. Thank you. Author misnumbered pages. ABSTRACT Title: Crack Growth During Brittle Fracture in Compression. Author: Bartlett W. Paulding, Jr. Submitted to the Department of Geology and Geophysics February 9, 1965 in partial fulfillment of the requirements for the degree of Doctor of Philosophy at the Massachusetts Institute of Technology. Photoelastic analysis of several two-crack arrays pre- dicts that compressive fracture is initiated at cracks oriented in a particular en schelon manner. Observation of partially-fractured samples of Westerly granite, obtained during uniaxial and confined compression tests by stopping the fracture process, indicate that fracture is initiated by en echelon arrays of biotite grains and pre-existing, trans-granular, cracks. -
Fringe Season 1 Transcripts
PROLOGUE Flight 627 - A Contagious Event (Glatterflug Airlines Flight 627 is enroute from Hamburg, Germany to Boston, Massachusetts) ANNOUNCEMENT: ... ist eingeschaltet. Befestigen sie bitte ihre Sicherheitsgürtel. ANNOUNCEMENT: The Captain has turned on the fasten seat-belts sign. Please make sure your seatbelts are securely fastened. GERMAN WOMAN: Ich möchte sehen wie der Film weitergeht. (I would like to see the film continue) MAN FROM DENVER: I don't speak German. I'm from Denver. GERMAN WOMAN: Dies ist mein erster Flug. (this is my first flight) MAN FROM DENVER: I'm from Denver. ANNOUNCEMENT: Wir durchfliegen jetzt starke Turbulenzen. Nehmen sie bitte ihre Plätze ein. (we are flying through strong turbulence. please return to your seats) INDIAN MAN: Hey, friend. It's just an electrical storm. MORGAN STEIG: I understand. INDIAN MAN: Here. Gum? MORGAN STEIG: No, thank you. FLIGHT ATTENDANT: Mein Herr, sie müssen sich hinsetzen! (sir, you must sit down) Beruhigen sie sich! (calm down!) Beruhigen sie sich! (calm down!) Entschuldigen sie bitte! Gehen sie zu ihrem Sitz zurück! [please, go back to your seat!] FLIGHT ATTENDANT: (on phone) Kapitän! Wir haben eine Notsituation! (Captain, we have a difficult situation!) PILOT: ... gibt eine Not-... (... if necessary...) Sprechen sie mit mir! (talk to me) Was zum Teufel passiert! (what the hell is going on?) Beruhigen ... (...calm down...) Warum antworten sie mir nicht! (why don't you answer me?) Reden sie mit mir! (talk to me) ACT I Turnpike Motel - A Romantic Interlude OLIVIA: Oh my god! JOHN: What? OLIVIA: This bed is loud. JOHN: You think? OLIVIA: We can't keep doing this. -

Amplitude Inversion of Fast and Slow Converted Waves for Fracture Characterization of the Montney Formation in Pouce Coupe Field, Alberta, Canada
AMPLITUDE INVERSION OF FAST AND SLOW CONVERTED WAVES FOR FRACTURE CHARACTERIZATION OF THE MONTNEY FORMATION IN POUCE COUPE FIELD, ALBERTA, CANADA by Tyler L. MacFarlane c Copyright by Tyler L. MacFarlane, 2014 All Rights Reserved A thesis submitted to the Faculty and the Board of Trustees of the Colorado School of Mines in partial fulfillment of the requirements for the degree of Master of Science (Geo- physics). Golden, Colorado Date Signed: Tyler L. MacFarlane Signed: Dr. Thomas L. Davis Thesis Advisor Golden, Colorado Date Signed: Dr. Terence K. Young Professor and Head Department of Geophysics ii ABSTRACT The Montney Formation of western Canada is one of the largest economically viable gas resource plays in North America with reserves of 449TCF. As an unconventional tight gas play, the well development costs are high due to the hydraulic stimulations necessary for economic success. The Pouce Coupe research project is a multidisciplinary collaboration between the Reservoir Characterization Project (RCP) and Talisman Energy Inc. with the objective of understanding the reservoir to enable the optimization of well placement and completion design. The work in this thesis focuses on identifying the natural fractures in the reservoir that act as the delivery systems for hydrocarbon flow to the wellbore. Characterization of the Montney Formation at Pouce Coupe is based on time-lapse mul- ticomponent seismic surveys that were acquired before and after the hydraulic stimulation of two horizontal wells. Since shear-wave velocities and amplitudes of the PS-waves are known to be sensitive to near-vertical fractures, I utilize isotropic simultaneous seismic in- versions on azimuthally-sectored PS1 and PS2 data sets to obtain measurements of the fast and slow shear-velocities. -

2019-06-30 LM Financial Statements AUDITED Final
LEGAL MOMENTUM FINANCIAL STATEMENTS JUNE 30, 2019 and 2018 INDEPENDENT AUDITORS' REPORT Board of Directors Legal Momentum New York, New York Report on the Financial Statements We have audited the accompanying financial statements of Legal Momentum (the "Organization"), which comprise the statements of financial position as of June 30, 2019 and 2018, and the related statements of activities, functional expenses, and cash flows for the years then ended, and the related notes to the financial statements. Management's Responsibility for the Financial Statements The Organization's management is responsible for the preparation and fair presentation of these financial statements in accordance with accounting principles generally accepted in the United States of America; this includes the design, implementation, and maintenance of internal control relevant to the preparation and fair presentation of financial statements that are free from material misstatement, whether due to fraud or error. Auditor's Responsibility Our responsibility is to express an opinion on these financial statements based on our audits. We conducted our audits in accordance with auditing standards generally accepted in the United States of America. Those standards require that we plan and perform the audit to obtain reasonable assurance about whether the financial statements are free from material misstatement. An audit involves performing procedures to obtain evidence about the amounts and disclosures in the financial statements. The procedures selected depend on the auditor's judgment, including the assessment of the risks of material misstatement of the financial statements, whether due to fraud or error. In making those risk assessments, the auditor considers internal control relevant to the entity's preparation and fair presentation of the financial statements, in order to design audit procedures that are appropriate in the circumstances, but not for the purpose of expressing an opinion on the effectiveness of the entity's internal control. -

'"There's More Than One of Everything": Navigating Fringe's Cofactual Multiverse'
. Volume 13, Issue 1 May 2016 ‘There’s More Than One of Everything’: Navigating Fringe’s cofactual multiverse Casey J. McCormick, McGill University, Montréal, Canada Abstract: This article analyzes how viewers of Fringe (FOX 2008-2013) make sense of the series’ complex science fictional storyworld. It argues that Fringe presents multiple iterations of worlds and characters in a way that encourages ‘cofactual’ interpretation: rather than figuring parallel universes and alternate timelines as ontologically hierarchical, the narrative accommodates all versions of reality and invites viewers to participate in shaping the multiverse. The article offers a close reading of Fringe’s complex narrative structure alongside an exploration of how audiences responded to and impacted the series through fannish practices such as vidding and narrative mapping. It concludes that cofactual narration opens up an array of participatory practices that blur the text/paratext distinction and facilitate interactive storyworld building. Keywords: Complex TV, Fandom, Narrative, Paratexts, Counterfactual, Cofactual, Possible Worlds Cofactual Interpretation By the time viewers reach the series finale of Fringe (FOX 2008-2013), they have travelled across two spatially-distinct universes, three versions of the future, and at least four different timelines, with each world-iteration populated by different versions of the show’s central characters. Through its reinvigoration of science fiction tropes, such as time travel, alternate realities, and temporal resets, Fringe asks viewers to re-evaluate typical models of narrative world-building. The series constructs a multiverse comprised of what I deem cofactual diegetic worlds. I use the term ‘cofactual’ in contradistinction to the more common narrative term ‘counterfactual’ as a means of emphasizing the plurality and simultaneity of diegetic worlds in Fringe. -

Creating an Omaha Fringe Festival
Omaha Fringe Festival UNO Theatre Graduate Program Tamar Neumann Creating an Omaha Fringe Festival Project Description: In 1947, after World War II, Edinburgh created an arts festival called Edinburgh International Festival. Eight artists, not invited to perform, showed up anyway and began performing on the fringes of the festival. Each year after that more performers showed up to the festival performing on the fringes, until 1958 when the official Festival Fringe Society was created. When the constitution for the Festival Fringe was written, they made sure to keep the integrity of those first performers by guaranteeing the festival would be a space open to anyone willing to perform. Today, the Edinburgh Fringe Festival is the biggest Fringe Festival in the world. From their example, artists all over the world have gravitated towards festivals that celebrate the arts in a similar way. A Fringe festival derives its name from those performers who began on the Fringes of the Edinburgh Festival Fringe. These festivals are simply a place where artists of all types can come together and perform or show their art. The works are generally performance based, self produced and self funded. In some cases the performers are all theatre based, but in others the festival can consist of musicians, stand up comics, theatre shows, and visual arts. Some festivals are open access, some are lottery, some are juried and some are a mix. After Edinburgh, Fringe festivals began to show up all over the world. Currently, the World Fringe website states there are over 250 Fringe festivals in countries from Europe to Africa to Asia to America. -
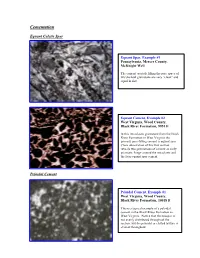
Ucementation
CementationU EquantU Calcite Spar PeloidalU Cement peloids. Equant Spar, Example #1 Pennsylvania, Mercer County, McKnight Well The cement crystals filling the pore space of this skeletal grainstone are very “clean” and equal in size. Equant Cement, Example #2 West Virginia, Wood County, Black River Formation, 9951 ft In this intraclastic grainstone from the Black River Formation in West Virginia the primary pore-filling cement is equant spar. Close observation of this thin section reveals two generations of cement an early prismatic fringe around the intraclasts and the later equant spar cement. PeloidalU Cement Peloidal Cement, Example #1 West Virginia, Wood County, Black River Formation, 10018 ft This is a typical example of a peloidal cement in the Black River Formation in West Virginia. Notice that the neospar is not evenly distributed throughout the section, but the peloidal or clotted texture is evident throughout. Peloidal Cement, Example #2 West Virginia, Wood County, Black River Formation, 10034 ft In this section the most distinct peloidal texture is evident in the lower left corner of the slide. In addition to the peloidal cement there are also wavy argillaceous laminations with associated dolomite crystals. Peloidal Cement, Example #3 Pennsylvania, Union Furnace outcrop The clotted texture of this mudstone shows the partial development of peloidal cement. Notice the somewhat rounded grains with sparry material in between. Further neomorphism will result in textures similar to those observed in the other peloidal cement slides. Peloidal Cement, Example #4 West Virginia, Wood County, Black River Formation, 10054 ft This peloidal cement was photographed under crossed polars. Notice the fuzzy grain boundaries between the peloids and the neospar DrusyU Spar Drusy Spar, Example #1 West Virginia, Wood County, Trenton Formation, 8495 ft Notice the different crystal sizes in this drusy calcite spar cement. -
Fracture-Related Fluid Flow in Sandstone Reservoirs: Insights from Outcrop Analogues of South-Eastern Utah
Fracture-related fluid flow in sandstone reservoirs: insights from outcrop analogues of south-eastern Utah Kei Ogata, Kim Senger, Alvar Braathen, Jan Tveranger, Elizabeth Petrie, James Evans Fault- and fold-related fracturing strongly influences the fluid circulation in the subsurface, thus being extremely important for CO2 storage exploration, especially in terms of reservoir connectivity and leakage. In this context, discrete regions of concentrated sub-parallel fracturing known as fracture corridors or swarms, are inferred to be preferential conduits for fluid migration. We investigate fracture corridors of the middle-late Jurassic Entrada and Curtis Formations of the northern Paradox Basin (Utah), which are characterized by discoloration (bleaching) due to oxide removal by circulating CO2- and/or hydrocarbon-charged fluids. The analyzed fracture corridors are located in the footwall of a km-scale, steep normal fault with displacement values on the order of hundreds of meters. These structures trend roughly perpendicular and subordinately parallel to the direction of the main fault, defining a systematic network on the hundreds of meters scale. The fracture corridors pinch- and fringe- out laterally and vertically in single, continuous fractures, following the axial zones of open fold systems related to the evolution of the main fault. On the basis of the presented data we hypothesize that fracture corridors developed along the hinge of anticlinal/synclinal folds represent preferred pathways for fluid migration rather than the main faults, connecting localized reservoirs at different structural levels up to the surface. Introduction Fracture corridors are narrow and laterally extensive zones of concentrated fracturing defined by sub- parallel trending fractures (Ozkaya et al., 2007). -

Experimental Investigation of Quasistatic and Dynamic Fracture
Experimental Investigation of Quasistatic and Dynamic Fracture Properties of Titanium Alloys Thesis by David Deloyd Anderson In Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy California Institute of Technology Pasadena, California 2002 (Submitted January 11, 2002) ii c 2002 David Deloyd Anderson All Rights Reserved iii Acknowledgments: I would like to thank my advisors, Dr. Rosakis and Dr. Ravichandran, for their help, support, ideas, and patience with my research and with my doings in general. Life is too complicated to allow exclusive focus on any one thing, even research, and they helped me in managing all. In addition to Drs. Rosakis and Ravichandran, I would first like to thank those on my thesis committee: Dr. Bhattacharya, Dr. Ust¨¨ undag, and Dr. Meyers (U.C.S.D.) for their time, comments, and suggestion. These are the people who reviewed my research, listened to my presentation, verbally poked and prodded me, and then with their handshakes and signatures made me a doctor. My research was funded by the Office of Naval Research by Dr. G. Yoder, Scientific Officer. Little research and training occurs without funding, so for their support I am grateful. I was also assisted by the Charles Lee Powell Foundation and the ARCS (Achievement Rewards for College Scientists— www.arcsfoundation.org) foundation. The latter group not only made it financially palatable to forsake the workforce for a higher education (while “supporting” a family), but they provided many opportunities for me to interact with their members and donors. This provided me with endless motivation to make good on their show of faith in me. -

Momentum 2016
2016 . Volume 1 Celebrating 100 Years Story on page 12 Hundreds came out to help paint the building with light as the team of volunteers from RIT and EIOH worked to capture this cover image. momentum | 2016 . volume 1 1 Director’s Message hanks to the support of many, Eastman Institute for Oral Health has undergone some exciting changes this year, and is well poised for many Tmore over the next several months. To mark our 100th anniversary, we are thrilled to announce The Future Starts Now Centennial Symposium and Gala, where participants will engage in dynamic scientific sessions from worldwide leaders in dentistry June 9-10, 2017. People from all over the world will gather, learn, network and celebrate. Dr. Eli Eliav In this special Centennial edition of Momentum, you’ll find all the details about the Symposium and Gala (story p. 6), and the many updates happening in our clinics, classrooms and labs. On behalf of all of us at EIOH, special recognition and gratitude are extended to Drs. Dennis Clements and Martha Ann Keels, who donated $500,000 to update the EIOH Pediatric Dentistry clinic (story p. 4), and to Mr. Joe Lobozzo who provided major funding for our new SMILEmobile (story p. 6). Their generosity and dedication to access and education are deeply appreciated. The growing need for treatment for patients with disabilities and patients with complex medical conditions On the Cover is undeniable. We are working diligently to close this gap. More than 300 people attended the Centennial First, the training program we established, thanks to a $3.5 Kickoff event, Shine a Light on Eastman Dental, and helped create this beautiful image of the iconic building.