Effects of Home-Away Sequencing on the Length of Best-Of-Seven Game Playoff Series
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
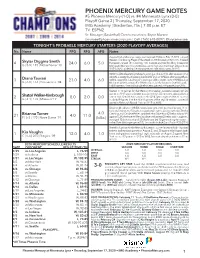
PHOENIX MERCURY GAME NOTES #5 Phoenix Mercury (1-0) Vs
PHOENIX MERCURY GAME NOTES #5 Phoenix Mercury (1-0) vs. #4 Minnesota Lynx (0-0) Playoff Game 2 | Thursday, September 17, 2020 IMG Academy | Bradenton, Fla. | 7:00 p.m. ET TV: ESPN2 Sr. Manager, Basketball Communications: Bryce Marsee [email protected] | Cell: (765) 618-0897 | @brycemarsee TONIGHT'S PROBABLE MERCURY STARTERS (2020 PLAYOFF AVERAGES) No. Name PPG RPG APG Notes Aquired by the Mercury in a sign-and-trade with Dallas on Feb. 12, 2020...named Western Conference Player of the Week on 9/8 for week of 8/31-9/6...finished 4 Skylar Diggins-Smith 24.0 6.0 5.0 the season ranked 7th in scoring, 10th in assists and tied for 4th in three-point G | 5-9 | 145 | Notre Dame '13 field goals (46)...scored a postseason career-high and team-high 24 points on 9/15 vs. WAS...picked up her first playoffs win over Washington on 9/15 WNBA's all-time leader in postseason scoring and ranks 3rd in all-time assists in the playoffs...6 assists shy of passing Sue Bird for 2nd on WNBA's all-time playoffs as- 3 Diana Taurasi 23.0 4.0 6.0 sists list...ranked 5th in the league in scoring and 8th in assists...led the WNBA in 3-pt G | 6-0 | 163 | Connecticut '04 field goals (61) this season, the 11th time she's led the league in 3-pt field goals... holds a perfect 7-0 record in single elimination games in the playoffs since 2016 Started in 10 games for the Mercury this season..scored a career-high 24 points on 9/11 against Seattle in a career-high 35 mimutes...also posted a 2 Shatori Walker-Kimbrough 8.0 2.0 0.0 career-high 5 steals this season in the 8/14 game against Atlanta...scored G | 6-1 | 170 | Missouri '19 in double figures 5 of the final 8 games of the regular season...scored 8 points in Mercury's Round 1 win on 9/15 vs. -

Quantifying How NBA Playoff Format Impacts Playoff Excitement
Quantifying How NBA Playoff Format Impacts Playoff Excitement Quinn Johnson, Bailey Fosdick, Connor Gibbs Colorado State University, Fort Collins, Colorado, United States Abbreviated abstract: The National Basketball Association has predominantly kept its same basic playoff format since 1984. Here, we explore two alternative playoff formats and quantify the expected excitement in game play across the playoffs. We consider format changes to include each conference's top 8 teams and playing a conference-less tournament, as well as, taking the top 16 teams in the NBA and playing a conference-less tournament. Using simulation, we found small to no differences in excitement between the three formats but continue to endorse the top 16 team system due its advantage in fairness to all teams. Related publications: – Tokarz D. How We Make the YUSAG Power Rankings. R: NBA Power Rankings. 2018 Mar 20. UCSAS [email protected] - 1 2020 Motivation Deserving teams are often left out Would changing the playoff format of postseason due to conference result in a drastically more or less strength differences. exciting postseason? Seeding Differences between Current and Top 16 Format Possible playoff formats Current play: conference who’s in: Top 8 West, Top 8 East –––––––––––––––––––––––––––––––––– 8W8E play: overall seeding who’s in: Top 8 West, Top 8 East –––––––––––––––––––––––––––––––––– 16TOT play: overall seeding who’s in: Top 16 NBA UCSAS 2020 Methods 1) Model win probability for each game 2) Simulate playoffs under different formats • Using -

Article 340 Playoffs #3400. All Playoffs Managed By
ARTICLE 340 PLAYOFFS #3400. ALL PLAYOFFS MANAGED BY COMMISSIONER All playoffs of the CIF Southern Section shall be under the management of the Commissioner of Athletics, who will have final authority and responsibility for their conduct. #3400.1 Enrollment based divisions will be used in the sports of boys and girls cross country and boys and girls track and field. By action of the Southern Section Council, once the divisions are established for the playoff, no school shall be allowed to move up to a larger enrollment division. Schools will participate based upon their CBED enrollment figures. Consideration will be given to geography after league placement has been recognized. #3400.2 No playoffs will be conducted by the CIF Southern Section Office when less than 20% of the membership field teams in that sport. #3400.3 See 54.8 (Emergency Powers). #3401. REPORT OF PLAYOFFS eAt the clos of the season for each sport, the Commissioner of Athletics shall compile a report of the playoffs in the “CIF Southern Section Bulletin.” #3402. IDENTIFYING LEAGUE REPRESENTATIVES INTO THE PLAYOFFS Under the playoff format ‐ in all sports ‐ leagues have the responsibility of developing and identifying the priority for their representatives into the playoffs. This will include the league’s priority with regard to any at‐large consideration. Thus, the league through its CIF Council Representative, MUST notify the CIF Southern Section Office prior to the playoff draw, the No. 1 representative, the No. 2 representative, the No. 3 representative, and the league’s priority team for consideration to any at‐large berth. -

Implementing Financial Fair Play Rules at Latvian-Estonian Basketball League
RIČARDS VAMBUTS IMPLEMENTING FINANCIAL FAIR PLAY RULES AT LATVIAN-ESTONIAN BASKETBALL LEAGUE Final Master Thesis Study programme: Sport Business Management State code 6211LX001 Supervisor: Assoc. prof. dr. Renata Legenzova Defended: Assoc. prof., dr. Rita Bendaravičienė Dean of the Faculty of Economics and Management Kaunas, 2021 Table of contents SUMMARY ........................................................................................................................................ 3 INTRODUCTION ............................................................................................................................... 4 I. LITERATURE REVIEW ON FINANCIAL FAIRPLAY AND FINANCIAL STABILITY ......... 6 1.1 The concept of financial stability in sports and its influencing factors ......................................... 6 1.2 Measures of financial stability ....................................................................................................... 8 1.3 Financial fair-play rules and their influence on financial stability in sports ............................... 11 1.4 Overview of financial fair-play rules in practices - cases of Euroleague and NBA .................... 15 II. ANALYSIS OF TEAMS' FINANCIAL STABILITY IN LATVIAN-ESTONIAN LEAGUE AND COMPARATIVE ANALYSIS OF FAIR-PLAY RULES ACROSS THE LEAGUES .......... 23 2.1 Overview of Latvian-Estonian basketball league ........................................................................ 23 2.2 Research methodology ................................................................................................................ -

League Rules & Regulations
LLEEAAGGUUEE RRUULLEESS && RREEGGUULLAATTIIOONNSS 1 TO ALL PLAYERS & PARTICIPANTS Welcome to Devil’s Den Beach Volleyball Centre. We are a co-ed adult recreational beach volleyball facility. We emphasize sportsmanship and mutual respect for all participants and are committed to providing fair play in a fun environment. We encourage team captains to work with the administration to ensure that it is enjoyable for all. All our leagues, no matter the skill level, are designed for social and recreational purposes and the rules and regulations are to be followed in accordance with this document. All rules and regulations outlined within this document have been modified from the official beach volleyball (F.I.V.B) Rule Book, to provide a satisfying and fun experience for all players involved. The Devil’s Den team would like to thank you for your past, present and future participation and would like to wish everyone a great season. Look forward to seeing you all on the sand and in the sun!!! Yours Sincerely, The Devil’s Den Team 2 TTAABBLLEE OOFF CCOONNTTEENNTTSS PART 1 – League Registrations……………….Page 4 Payment Schedule Registration Cancellations Choosing a League PART 2 - League Regulations………………….Page 6 Non-attendance Rosters & Waivers Weather Conditions League Co-ordinators Ball Deposits PART 3 – League Format ………….………...…Page 9 League Format League Standings League Divisions Playoff Format PART 4 – League Levels & Rules……………Page 13 Advanced & Intermediate 3’s/4’s Recreational 6’s PART 5 – The Teams ……………………………Page 17 Roster -

Playoff Format and Tiebreakers
PLAYOFF FORMAT FOR THE WOODBRIDGE TOWNSHIP MEN’S BASKETBALL LEAGUE THE TOP SIX (6) TEAMS WILL QUALIFY FOR THE PLAYOFFS. ALL ROUNDS ARE SINGLE ELIMINATION . THE TOP TWO (2) SEEDS WILL RECEIVE A FIRST ROUND BYE. FIRST ROUND OF PLAYOFFS a. THE NUMBER THREE (3) SEED WILL PLAY THE NUMBER (6) SIX SEED. b. THE NUMBER FOUR (4) SEED WILL PLAY THE NUMBER FIVE (5) SEED. SEMIFINAL ROUND OF PLAYOFFS a. THE NUMBER ONE (1) SEED WILL PLAY THE WINNER OF THE GAME BETWEEN THE NUMBER (4) AND NUMBER (5) SEED b. THE NUMBER TWO (2) SEED WILL PLAY THE WINNNER OF THE GAME BETWEEN THE NUMBER (3) AND THE NUMBER (6) SEED. CHAMPIONSHIP ROUND a. THE TWO LOSING TEAMS OF THE SEMIFINAL GAMES WILL PLAY FOR THIRD PLACE. b. THE TWO WINNING TEAMS OF THE SEMIFINAL GAMES WILL PLAY FOR THE LEAGUE CHAMPIONSHIP. WITH THE EXCEPTION OF THE TWO (2) CHAMPIONSHIP ROUND GAMES, REFEREE PAYMENTS ARE STILL PAID BY EACH TEAM. TIEBREAKER PROCEDURE In the event of a tie for post season positioning, the final standings will be determined by the following criteria: 1. “Head to Head” competition. 2. “Head to Head” point differential ( If tiebreaker 1 does not break the tie) This tiebreaker would only be used if more than two teams finish with identical records and “Head to Head” Competiton could not break the tie. 3. Total Points Against (If tiebreaker 1 or 2 does not break tie). This tiebreaker would only be used if more than two teams finish with identical records and tiebreakers 1 & 2 could not break the tie. -

Playoff Rules
Playoff Fall Ball Rules These rules are enforced for all divisions for post-season play unless specifically stated otherwise. Post-season rules apply ONLY in the post-season tournament. View division rules for specific rule exceptions. Playoff Format - All teams from all divisions will play in a modified double elimination post- season tournament. Once the final two teams are determined, the tournament becomes single elimination. Seeds will be determined by the place in which each team took in the regular season. Home Team - The home team is always the higher seed except when a higher seed has entered the winner's bracket from the loser's bracket. Borrowed Players - Borrowed players are not allowed in post-season play. Each post- season game must begin and end with at least eight (8) players per team. A forfeit will be entered for a team that cannot field at least eight (8) players. In the case that both teams cannot field eight (8) players, both teams will forfeit with the higher seeded team advancing, unless a make up game can be scheduled prior to the next round. Time Limits - There are no time limits for post-season play. Each game will be completed unless the Mercy Rule applies. Weather/Darkness Delays - Any post-season game that has started and cannot be completed due to weather, darkness or curfew will be suspended and resumed at a later date. Pitching - Pitching will reset at the start of each division's tournament. Pitching will reset every seven (7) calendar days. For example, if the tournament begins on a Tuesday, pitching will reset the following Tuesday and any subsequent Tuesdays. -

International Tournament Pool Play Format
TOURNAMENT RULES AND GUIDELINES International Tournament Pool Play Format Section I – Guidelines The Pool Play Format should only be used in divisions in which there is a reasonable expectation for all teams to play all games for which they are scheduled . In divisions in which teams traditionally drop out at the last moment, or partway through the tournament, the standard double-elimination or single-elimination formats should be used instead . The following conditions must apply to all Pool Play Format tournaments, unless specified as optional: A . In the event a team or teams drop out of a pool play format tournament before the first game of the tournament is played (by any team in the tournament), the pools must be redrawn . If a team or teams drop out or is/are removed by action of the Tournament Committee after the first game is played, the matter must be referred to the Tournament Committee for a decision . B . A Pool Play Format tournament may have one or more pools . C . The pool assignments (or “draw”) must either be a blind draw, or must be based on geographic considerations . Pool assignments must never be “seeded” based on the expected ability of the teams . D . In all cases, the results of Pool Play have no bearing on the next segment of play, with the exception of rules and regulations regarding rest periods for pitchers, (i .e ., losses do not “carry over”) . E . It is preferable for each team in a given pool to be scheduled to play all other teams in that pool once . -

2021 Tournament Rules
2021 Tournament Rules 1. Each team will provide a contact person and phone number for which they can be reached during the tournament. 2. There will be no time outs during round robin play. During playoff games each team will be permitted one-thirty second time out. 3. All teams must be prepared to play their games fifteen minutes prior to scheduled start time in the event the tournament is ahead of schedule. Games will not start earlier than 15 minutes ahead of time unless agreed to by both teams and assuring that referee’s and timekeeper are ready to go early as well. 4. Tournament officials will consider any logical grievance, or suggestion when presented in a calm and professional manner. Protests regarding officiating will not be heard. 5. All Tournament rules will be interpreted in a manner consistent with the objectives of the tournament; A decision by the Tournament Director(s), whether specifically addressed by these rules, shall be binding upon all tournament participants. The Tournament Director(s) shall have the authority to grant exemptions from or make modifications to any of the rules when he considers it fair and appropriate to do so in any specific situation. All decisions by the Tournament Director(s) are final. 6. Teams need to bring their own pucks for games. The Ford Ice Center will provide pucks but please make sure you have 10-15 of your own as backup. Round Robin and consolation Game Format: a. 3-minute warm-up/15-15-15-minute period lengths b. Three-minute 3v3 sudden death OT i. -

Fall Sports Sports By-Laws Playoff Packets
Fall Sports Sports By-laws Playoff Packets Table of Contents Cross Country By-laws 1 Cross Country League Meet 5 Football By-laws 6 Golf By-laws 9 Golf Team Championship 12 Golf Individual Championship 13 Soccer By-laws 14 Soccer Playoff Packet 18 Volleyball By-laws 20 Volleyball Playoff Packet 23 SCHUYLKILL CROSS COUNTRY LEAGUE BY-LAWS IN AFFILIATION WITH THE SCHUYLKILL LEAGUE REVISED: June 2014 ARTICLE I – NAME The League shall be known as the Schuylkill Cross Country League. ARTICLE II – CROSS COUNTRY LEAGUE OFFICERS Section 1 The League Chairperson shall be a principal of a member school who has been appointed by the Schuylkill League President. Section 2 The chairperson may appoint other officers as deemed necessary. Section 3 The chairperson may recommend to the Schuylkill League a statistician if deemed necessary. ARTICLE III – CROSS COUNTRY LEAGUE MEETINGS Section 1 The chairperson shall conduct a meeting prior to the Fall Meeting of the Schuylkill League. The chairperson may also call additional meetings at his or her discretion. Section 2 Special meetings may be called by the chairperson upon written request of a member school. ARTICLE IV – DUES AND BUDGET Section 1 Dues and a budget shall be proposed at the pre-season meeting and submitted to the Schuylkill League for adoption at the Spring Meeting. ARTICLE V – MEMBERSHIP/ALLIGNMENT Section 1 The cross country league shall have two divisions named Division I and Division II. Section 2 Each division shall have an equal number of member schools whenever possible. Section 3 Divisions shall be based on enrollment. -

June 18 - June 24, 2021 Vol
June 18 - June 24, 2021 Vol. 19, Issue 43 www.sportspagdfw.com FREE 2 June 18, 2021 - June 24, 2021 | The Sports Page Weekly | Volume 19 Issue 43 | www.sportspagedfw.com | follow us on twitter @sportspagdfw.com Follow us on twitter @sportspagedfw | www.sportspagedfw.com | The Sports Page Weekly | Volume 19 - Issue 43 | June 18, 2021 - June 24, 2021 3 June 17, 2021 - June 24, 2021 AROUND THE AREA Vol. 19, Issue 43 LOCAL NEWS OF INTEREST sportspagedfw.com Established 2002 Doncic earns All-NBA first team Cover Photo: AROUND THE AREA the league MVP Nikola Joki led Denver in history to average at least 35-7-10 in a 4 all three this season). playoff series. RANGERS REPORT After recording a league-high 50 20-5-5 Doncic led Dallas outright in points and 5 BY DIC HUMPHREY games in 2019-20, Doncic finished second assists in all seven games, joining Oscar GOLF, ETC to Joki (50) with 49 such games in 2020-21. Robertson (1963 conference finals vs. 6 BY TOM WARD The former EuroLeague MVP also finished BOS) and James (2018 first round vs. U.S OPEN CHAMPIONSHIP second to Portland’s Damian Lillard (60) IND) as the only players in league history 7 BY PGATOUR.COM Luka Doncic earns second consecutive with 57 20-point games and ranked third in to lead their team in points and assists in NINE THINGS TO KNOW ABOUT All-NBA first team selection 25-point games (45) and fourth in 30-point all seven games of a series. 8 TORREY PINES Mavericks guard Luka Doncic was efforts (26) and triple-doubles (11). -

NBA Playoff Format Is Optimizing Competitive Balance by Eliminating Travel 26 August 2020
NBA playoff format is optimizing competitive balance by eliminating travel 26 August 2020 predicted probabilities of winning than teams that traveled west or played in the same time zone. In contrast, teams that traveled west across three time zones had lower predicted win probabilities than teams that traveled east or played in the same time zone. "During this initial study, it was interesting to find that team scoring improved during general eastward travel compared to westward travel and travel in the same zone, but game outcomes were unaffected by direction of travel during the playoffs," said lead author Sean Pradhan, assistant professor of sports management and business analytics in the School of Business Administration Credit: CC0 Public Domain at Menlo College in Atherton, California. "However, when considering the magnitude of travel across different time zones, we found that teams had predicted probabilities of winning that were lower In addition to helping protect players from after traveling three time zones westward, and COVID-19, the NBA 'bubble' in Orlando may be a tended to actually lose more games when traveling competitive equalizer by eliminating team travel. two time zones westward compared to most other Researchers analyzing the results of nearly 500 types of travel." NBA playoff games over six seasons found that a team's direction of travel and the number of time Circadian rhythms are endogenous, near-24-hour zones crossed were associated with its predicted biological rhythms that exist in all living organisms, win probability and actual game performance. and these daily rhythms have peaks and troughs in both alertness and sleepiness that can impact Preliminary results of the study suggest that the individuals in high-performance professions.