DOCSLIB.ORG

Normed Vector Spaces

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Normed Vector Spaces Chapter II Elements of Functional Analysis Functional Analysis is generally understood a “linear algebra for infinite di- mensional vector spaces.” Most of the vector spaces that are used are spaces of (various types of) functions, therfeore the name “functional.” This chapter in- troduces the reader to some very basic results in Functional Analysis. The more motivated reader is suggested to continue with more in depth texts. 1. Normed vector spaces Definition. Let K be one of the fields R or C, and let X be a K-vector space. A norm on X is a map X 3 x 7−→ kxk ∈ [0, ∞) with the following properties (i) kx + yk ≤ kxk + kyk, ∀ x, y ∈ X; (ii) kλxk = |λ| · kxk, ∀ x ∈ X, λ ∈ K; (iii) kxk = 0 =⇒ x = 0. (Note that conditions (i) and (ii) state that k . k is a seminorm.) Examples 1.1. Let K be either R or C, and let J be some non-empty set. A. Define `∞(J) = α : J → : sup |α(j)| < ∞ . K K j∈J We equip the space `∞(J) with the -vector space structure defined by point-wise K K addition and point-wise scalar multiplication. This vector space carries a natural norm k . k∞, defined by kαk = sup |α(j)|, α ∈ `∞(I). ∞ K j∈J When = , the space `∞(J) is simply denoted by `∞(J). When J = - the set K C C N of natural numbers - instead of `∞( ) we simply write `∞, and instead of `∞( ) R N R N we simply write `∞. B. Consider the space K c0 (J) = α : J → K : inf sup |α(j)| = 0 . F ⊂J j∈J F finite r K Remark that, if we equip J with the discrete topology, then c0 (J) is the space of those (automatically continuous) functions : J → K which have limit 0 at ∞. In particular, cK(J) is a linear subspace of `∞(J). We also equip cK(J) with the norm 0 K 0 k . k∞. As above, when K = C, we ommit it from the notation, and when J = N, we also ommit it. 1 2 CHAPTER II: ELEMENTS OF FUNCTIONAL ANALYSIS Definition. Suppose X is a normed vector space, with norm k . k. Then there is a natural metric d on X, defined by d(x, y) = kx − yk, x, y ∈ X. The toplogy on X, defined by this metric, is called the norm topology. Exercise 1 ♦. Let X be a normed vector space, over K(= R, C). Prove that, when equipped with the norm toplogy, X becomes a topological vector space. That is, the maps X × X 3 (x, y) 7−→ x + y ∈ X K × X 3 (λ, x) 7−→ λx ∈ X are continuous. Exercise 2 ♦. Let K be one of the fields R or C, and let J be a non-empty set. A. Prove that cK(J) is a closed linear subspace in `∞(J). 0 K B. Recall (see I.2) that for a function α : J → K we denoted by [[α]] the support of α, defined as [[α]] = {j ∈ J : α(j) 6= 0}. Consider the space fin (J) = α : J → : [[α]] finite . K K Prove that fin (J) is a linear subspace in cK(J), which is dense in the K 0 norm topology. The next example is based on the notion of summability discussed in I.2. Example 1.2. Let K be either R or C, let J be a non-empty set, and let p ∈ [1, ∞) be a real number. We define `p (J) = α : J → : |α|p : J → [0, ∞) summable . K K Remark that fin (I) ⊂ `q (J). K K For α ∈ `p (J) we define K 1 p X p kαkp = |α(j)| . j∈J When = , the space `p (J) is simply denoted by `p(J). When J = - K C C N the set of natural numbers - instead of `p ( ) we simply write `p , and instead of R N R `p(N) we simply write `p. The proof of the fact that the `p spaces (1 ≤ p < ∞) are normed vector spaces is included in the following exercises. To make the formulation a little easier, we use the following terminology. Definition. Two “numbers” p, q ∈ [1, ∞] are said to be H¨olderconjugate, if 1 1 1 p + q = 1. Here we use the convention ∞ = 0. Exercise 3 ♦. Let K be one of the fields R or C, let J be a non-empty set, and let p, q ∈ [1, ∞] be two H¨older conjugate “numbers.” Consider the set q B (J) = β ∈ fin (J): kβkq ≤ 1 , K K §1. Normed vector spaces 3 and define, for functions α : J → and β ∈ fin (J), the quantity K K X hα, βi = α(j)β(j). j∈[[β]] Prove that, for α : J → K, the following are equivalent: (i) α ∈ `p (J); K (ii) sup |hα, βi| < ∞. β∈Bq (J) K Moreover, one has the equality p sup |hα, βi| = kαkp, ∀ α ∈ ` (J). K β∈Bq (J) K Hint: Use H¨older inequality (Appendix D). Exercise 4 ♦. Let K be either R or C, let J be a non-empty set, and let p ∈ [1, ∞). Prove that, when equipped with pointwise addition and scalar mul- p tiplication, then (` (J), k .kp) is a normed vector space. K Hint: Use the preceding exercise. Exercise 5 ♦. Let K be one of the fields R or C, let J be a non-empty set, and let p, q ∈ [1, ∞] be two H¨older conjugate “numbers.” A. If α ∈ `p (J) and β ∈ `q (J), then αβ ∈ `1 (J), and K K K kαβk1 ≤ kαkp · kβkq. B. Using part A, extend the pairing constructed in Exercise 3 to a bilinear map h .,. i : `p (J) × `q (J) → , defined by K K K X hα, βi = α(j)β(j), ∀ α ∈ `p (J), β ∈ `q (J). K K j∈J C. Prove that, for every α ∈ `p (J), one has the equality K q kαkp = sup {|hα, βi| : β ∈ ` (J), kβkq ≤ 1} . K Exercise 6 ♦. Let K be one of the fields R or C, and let J be a non-empty set. A. Prove that fin (J) is a dense linear subspace in `p (J), for every p ∈ [1, ∞). K K B. Why was the case p = ∞ ommitted? We now examine linear continuous maps between normed spaces. Proposition 1.1. Let K be either R or C, let X and Y be normed K-vector spaces, and let T : X → Y be a K-linear map. The following are equivalent: (i) T is continuous; (ii) sup kT xk : x ∈ X, kxk ≤ 1 < ∞; (iii) sup kT xk : x ∈ X, kxk = 1 < ∞; (iv) T is continuous at 0. Proof. (i) ⇒ (ii). Assume T is continuous, but sup kT xk : x ∈ X, kxk ≤ 1 < ∞, which means there exists some sequence (xn)n≥1 ⊂ X such that (a) kxnk ≤ 1, ∀ n ≥ 1; (b) limn→∞ kT xnk = ∞. 4 CHAPTER II: ELEMENTS OF FUNCTIONAL ANALYSIS Put −1 zn = kT xnk xn, ∀ n ≥ 1. On the one hand, we have kxnk 1 kznk = ≤ , ∀ n ≥ 1, kT xnk kT xnk which gives limn→∞ kznk = 0, i.e. limn→∞ zn = 0. Since T is assumed to be continuous, we will get (1) lim T zn = T 0 = 0. n→∞ −1 On the other hand, since T is linear, we have T zn = kT xnk T xn, so in particular we get kT znk = 1, ∀ n ≥ 1, which clearly contradicts (1). (ii) ⇒ (iii). This is obvious, since the supremum in (iii) is taken over a subset of the set used in (ii). (iii) ⇒ (iv). Let (xn)n≥1 ⊂ X be a sequence with limn→∞ xn = 0. For each n ≥ 1, define −1 kxnk xn, if xn 6= 0 un = any vector of norm 1, if xn = 0 so that we have kunk = 1 and xn = kxnkun, ∀ n ≥ 1. Since T is linear, we have (2) T xn = kxnkT un, ∀ n ≥ 1. If we define M = sup kT xk : x ∈ X, kxk = 1 , then kT unk ≤ M, ∀ n ≥ 1, so (2) will give kT xnk ≤ M · kxnk, ∀ n ≥ 1, and the condition limn→∞ xn = 0 will force limn→∞ T xn = 0. (iv) ⇒ (i). Assume T is continuous at 0, and let us prove that T is continuous at any point. Start with some arbitrary x ∈ X and an arbitrary sequence (xn)n≥1 ⊂ X with limn→∞ xn = x. Put zn = xn − x, so that limn→∞ zn = 0. Then we will have limn→∞ T zn = 0, which (use the linearity of T ) means that 0 = lim kT znk = lim kT xn − T xk, n→∞ n→∞ thus proving that limn→∞ T xn = T x. Remark 1.1. Using the notations above, the quantities in (ii) and (iii) are in fact equal. Indeed, if we define M1 = sup kT xk : x ∈ X, kxk ≤ 1 , M2 = sup kT xk : x ∈ X, kxk = 1 , then as observed during the proof, we have M2 ≤ M1. Conversely, if we start with some arbitrary x ∈ X with kxk ≤ 1, then we can always write x = kxku, for some u ∈ X with kuk = 1. In particular we will get kT xk = kxk · kT uk ≤ kxk · M2 ≤ M2. §1. Normed vector spaces 5 Taking supremum in the above inequality, over all x ∈ X with kxk ≤ 1, will then give the inequality M1 ≤ M2. Notations. Let K be either R or C, and let X and Y be normed K-vector spaces. We define L(X, Y) = T : X → Y : T K-linear and continuous . For T ∈ L(X, Y) we define (see the above remark) kT k = sup kT xk : x ∈ X, kxk ≤ 1 = sup kT xk : x ∈ X, kxk = 1 When Y = K (equipped with the absolute value as the norm), the space L(X, K) will be denoted simply by X∗, and will be called the topological dual of X.
Load more

Recommended publications
  • Functional Analysis Lecture Notes Chapter 3. Banach
    FUNCTIONAL ANALYSIS LECTURE NOTES CHAPTER 3. BANACH SPACES CHRISTOPHER HEIL 1. Elementary Properties and Examples Notation 1.1. Throughout, F will denote either the real line R or the complex plane C. All vector spaces are assumed to be over the field F. Definition 1.2. Let X be a vector space over the field F. Then a semi-norm on X is a function k · k: X ! R such that (a) kxk ≥ 0 for all x 2 X, (b) kαxk = jαj kxk for all x 2 X and α 2 F, (c) Triangle Inequality: kx + yk ≤ kxk + kyk for all x, y 2 X. A norm on X is a semi-norm which also satisfies: (d) kxk = 0 =) x = 0. A vector space X together with a norm k · k is called a normed linear space, a normed vector space, or simply a normed space. Definition 1.3. Let I be a finite or countable index set (for example, I = f1; : : : ; Ng if finite, or I = N or Z if infinite). Let w : I ! [0; 1). Given a sequence of scalars x = (xi)i2I , set 1=p jx jp w(i)p ; 0 < p < 1; 8 i kxkp;w = > Xi2I <> sup jxij w(i); p = 1; i2I > where these quantities could be infinite.:> Then we set p `w(I) = x = (xi)i2I : kxkp < 1 : n o p p p We call `w(I) a weighted ` space, and often denote it just by `w (especially if I = N). If p p w(i) = 1 for all i, then we simply call this space ` (I) or ` and write k · kp instead of k · kp;w.
    [Show full text]
  • Elements of Linear Algebra, Topology, and Calculus
    00˙AMS September 23, 2007 © Copyright, Princeton University Press. No part of this book may be distributed, posted, or reproduced in any form by digital or mechanical means without prior written permission of the publisher. Appendix A Elements of Linear Algebra, Topology, and Calculus A.1 LINEAR ALGEBRA We follow the usual conventions of matrix computations. Rn×p is the set of all n p real matrices (m rows and p columns). Rn is the set Rn×1 of column vectors× with n real entries. A(i, j) denotes the i, j entry (ith row, jth column) of the matrix A. Given A Rm×n and B Rn×p, the matrix product Rm×p ∈ n ∈ AB is defined by (AB)(i, j) = k=1 A(i, k)B(k, j), i = 1, . , m, j = 1∈, . , p. AT is the transpose of the matrix A:(AT )(i, j) = A(j, i). The entries A(i, i) form the diagonal of A. A Pmatrix is square if is has the same number of rows and columns. When A and B are square matrices of the same dimension, [A, B] = AB BA is termed the commutator of A and B. A matrix A is symmetric if −AT = A and skew-symmetric if AT = A. The commutator of two symmetric matrices or two skew-symmetric matrices− is symmetric, and the commutator of a symmetric and a skew-symmetric matrix is skew-symmetric. The trace of A is the sum of the diagonal elements of A, min(n,p ) tr(A) = A(i, i). i=1 X We have the following properties (assuming that A and B have adequate dimensions) tr(A) = tr(AT ), (A.1a) tr(AB) = tr(BA), (A.1b) tr([A, B]) = 0, (A.1c) tr(B) = 0 if BT = B, (A.1d) − tr(AB) = 0 if AT = A and BT = B.
    [Show full text]
  • Functional Analysis 1 Winter Semester 2013-14
    Functional analysis 1 Winter semester 2013-14 1. Topological vector spaces Basic notions. Notation. (a) The symbol F stands for the set of all reals or for the set of all complex numbers. (b) Let (X; τ) be a topological space and x 2 X. An open set G containing x is called neigh- borhood of x. We denote τ(x) = fG 2 τ; x 2 Gg. Definition. Suppose that τ is a topology on a vector space X over F such that • (X; τ) is T1, i.e., fxg is a closed set for every x 2 X, and • the vector space operations are continuous with respect to τ, i.e., +: X × X ! X and ·: F × X ! X are continuous. Under these conditions, τ is said to be a vector topology on X and (X; +; ·; τ) is a topological vector space (TVS). Remark. Let X be a TVS. (a) For every a 2 X the mapping x 7! x + a is a homeomorphism of X onto X. (b) For every λ 2 F n f0g the mapping x 7! λx is a homeomorphism of X onto X. Definition. Let X be a vector space over F. We say that A ⊂ X is • balanced if for every α 2 F, jαj ≤ 1, we have αA ⊂ A, • absorbing if for every x 2 X there exists t 2 R; t > 0; such that x 2 tA, • symmetric if A = −A. Definition. Let X be a TVS and A ⊂ X. We say that A is bounded if for every V 2 τ(0) there exists s > 0 such that for every t > s we have A ⊂ tV .
    [Show full text]
  • HYPERCYCLIC SUBSPACES in FRÉCHET SPACES 1. Introduction
    PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 134, Number 7, Pages 1955–1961 S 0002-9939(05)08242-0 Article electronically published on December 16, 2005 HYPERCYCLIC SUBSPACES IN FRECHET´ SPACES L. BERNAL-GONZALEZ´ (Communicated by N. Tomczak-Jaegermann) Dedicated to the memory of Professor Miguel de Guzm´an, who died in April 2004 Abstract. In this note, we show that every infinite-dimensional separable Fr´echet space admitting a continuous norm supports an operator for which there is an infinite-dimensional closed subspace consisting, except for zero, of hypercyclic vectors. The family of such operators is even dense in the space of bounded operators when endowed with the strong operator topology. This completes the earlier work of several authors. 1. Introduction and notation Throughout this paper, the following standard notation will be used: N is the set of positive integers, R is the real line, and C is the complex plane. The symbols (mk), (nk) will stand for strictly increasing sequences in N.IfX, Y are (Hausdorff) topological vector spaces (TVSs) over the same field K = R or C,thenL(X, Y ) will denote the space of continuous linear mappings from X into Y , while L(X)isthe class of operators on X,thatis,L(X)=L(X, X). The strong operator topology (SOT) in L(X) is the one where the convergence is defined as pointwise convergence at every x ∈ X. A sequence (Tn) ⊂ L(X, Y )issaidtobeuniversal or hypercyclic provided there exists some vector x0 ∈ X—called hypercyclic for the sequence (Tn)—such that its orbit {Tnx0 : n ∈ N} under (Tn)isdenseinY .
    [Show full text]
  • Linear Spaces
    Chapter 2 Linear Spaces Contents FieldofScalars ........................................ ............. 2.2 VectorSpaces ........................................ .............. 2.3 Subspaces .......................................... .............. 2.5 Sumofsubsets........................................ .............. 2.5 Linearcombinations..................................... .............. 2.6 Linearindependence................................... ................ 2.7 BasisandDimension ..................................... ............. 2.7 Convexity ............................................ ............ 2.8 Normedlinearspaces ................................... ............... 2.9 The `p and Lp spaces ............................................. 2.10 Topologicalconcepts ................................... ............... 2.12 Opensets ............................................ ............ 2.13 Closedsets........................................... ............. 2.14 Boundedsets......................................... .............. 2.15 Convergence of sequences . ................... 2.16 Series .............................................. ............ 2.17 Cauchysequences .................................... ................ 2.18 Banachspaces....................................... ............... 2.19 Completesubsets ....................................... ............. 2.19 Transformations ...................................... ............... 2.21 Lineartransformations.................................. ................ 2.21
    [Show full text]
  • L P and Sobolev Spaces
    NOTES ON Lp AND SOBOLEV SPACES STEVE SHKOLLER 1. Lp spaces 1.1. Definitions and basic properties. Definition 1.1. Let 0 < p < 1 and let (X; M; µ) denote a measure space. If f : X ! R is a measurable function, then we define 1 Z p p kfkLp(X) := jfj dx and kfkL1(X) := ess supx2X jf(x)j : X Note that kfkLp(X) may take the value 1. Definition 1.2. The space Lp(X) is the set p L (X) = ff : X ! R j kfkLp(X) < 1g : The space Lp(X) satisfies the following vector space properties: (1) For each α 2 R, if f 2 Lp(X) then αf 2 Lp(X); (2) If f; g 2 Lp(X), then jf + gjp ≤ 2p−1(jfjp + jgjp) ; so that f + g 2 Lp(X). (3) The triangle inequality is valid if p ≥ 1. The most interesting cases are p = 1; 2; 1, while all of the Lp arise often in nonlinear estimates. Definition 1.3. The space lp, called \little Lp", will be useful when we introduce Sobolev spaces on the torus and the Fourier series. For 1 ≤ p < 1, we set ( 1 ) p 1 X p l = fxngn=1 j jxnj < 1 : n=1 1.2. Basic inequalities. Lemma 1.4. For λ 2 (0; 1), xλ ≤ (1 − λ) + λx. Proof. Set f(x) = (1 − λ) + λx − xλ; hence, f 0(x) = λ − λxλ−1 = 0 if and only if λ(1 − xλ−1) = 0 so that x = 1 is the critical point of f. In particular, the minimum occurs at x = 1 with value f(1) = 0 ≤ (1 − λ) + λx − xλ : Lemma 1.5.
    [Show full text]
  • Fact Sheet Functional Analysis
    Fact Sheet Functional Analysis Literature: Hackbusch, W.: Theorie und Numerik elliptischer Differentialgleichungen. Teubner, 1986. Knabner, P., Angermann, L.: Numerik partieller Differentialgleichungen. Springer, 2000. Triebel, H.: H¨ohere Analysis. Harri Deutsch, 1980. Dobrowolski, M.: Angewandte Funktionalanalysis, Springer, 2010. 1. Banach- and Hilbert spaces Let V be a real vector space. Normed space: A norm is a mapping k · k : V ! [0; 1), such that: kuk = 0 , u = 0; (definiteness) kαuk = jαj · kuk; α 2 R; u 2 V; (positive scalability) ku + vk ≤ kuk + kvk; u; v 2 V: (triangle inequality) The pairing (V; k · k) is called a normed space. Seminorm: In contrast to a norm there may be elements u 6= 0 such that kuk = 0. It still holds kuk = 0 if u = 0. Comparison of two norms: Two norms k · k1, k · k2 are called equivalent if there is a constant C such that: −1 C kuk1 ≤ kuk2 ≤ Ckuk1; u 2 V: If only one of these inequalities can be fulfilled, e.g. kuk2 ≤ Ckuk1; u 2 V; the norm k · k1 is called stronger than the norm k · k2. k · k2 is called weaker than k · k1. Topology: In every normed space a canonical topology can be defined. A subset U ⊂ V is called open if for every u 2 U there exists a " > 0 such that B"(u) = fv 2 V : ku − vk < "g ⊂ U: Convergence: A sequence vn converges to v w.r.t. the norm k · k if lim kvn − vk = 0: n!1 1 A sequence vn ⊂ V is called Cauchy sequence, if supfkvn − vmk : n; m ≥ kg ! 0 for k ! 1.
    [Show full text]
  • Inner Product Spaces Isaiah Lankham, Bruno Nachtergaele, Anne Schilling (March 2, 2007)
    MAT067 University of California, Davis Winter 2007 Inner Product Spaces Isaiah Lankham, Bruno Nachtergaele, Anne Schilling (March 2, 2007) The abstract definition of vector spaces only takes into account algebraic properties for the addition and scalar multiplication of vectors. For vectors in Rn, for example, we also have geometric intuition which involves the length of vectors or angles between vectors. In this section we discuss inner product spaces, which are vector spaces with an inner product defined on them, which allow us to introduce the notion of length (or norm) of vectors and concepts such as orthogonality. 1 Inner product In this section V is a finite-dimensional, nonzero vector space over F. Definition 1. An inner product on V is a map ·, · : V × V → F (u, v) →u, v with the following properties: 1. Linearity in first slot: u + v, w = u, w + v, w for all u, v, w ∈ V and au, v = au, v; 2. Positivity: v, v≥0 for all v ∈ V ; 3. Positive definiteness: v, v =0ifandonlyifv =0; 4. Conjugate symmetry: u, v = v, u for all u, v ∈ V . Remark 1. Recall that every real number x ∈ R equals its complex conjugate. Hence for real vector spaces the condition about conjugate symmetry becomes symmetry. Definition 2. An inner product space is a vector space over F together with an inner product ·, ·. Copyright c 2007 by the authors. These lecture notes may be reproduced in their entirety for non- commercial purposes. 2NORMS 2 Example 1. V = Fn n u =(u1,...,un),v =(v1,...,vn) ∈ F Then n u, v = uivi.
    [Show full text]
  • Basic Differentiable Calculus Review
    Basic Differentiable Calculus Review Jimmie Lawson Department of Mathematics Louisiana State University Spring, 2003 1 Introduction Basic facts about the multivariable differentiable calculus are needed as back- ground for differentiable geometry and its applications. The purpose of these notes is to recall some of these facts. We state the results in the general context of Banach spaces, although we are specifically concerned with the finite-dimensional setting, specifically that of Rn. Let U be an open set of Rn. A function f : U ! R is said to be a Cr map for 0 ≤ r ≤ 1 if all partial derivatives up through order r exist for all points of U and are continuous. In the extreme cases C0 means that f is continuous and C1 means that all partials of all orders exists and are continuous on m r r U. A function f : U ! R is a C map if fi := πif is C for i = 1; : : : ; m, m th where πi : R ! R is the i projection map defined by πi(x1; : : : ; xm) = xi. It is a standard result that mixed partials of degree less than or equal to r and of the same type up to interchanges of order are equal for a C r-function (sometimes called Clairaut's Theorem). We can consider a category with objects nonempty open subsets of Rn for various n and morphisms Cr-maps. This is indeed a category, since the composition of Cr maps is again a Cr map. 1 2 Normed Spaces and Bounded Linear Oper- ators At the heart of the differential calculus is the notion of a differentiable func- tion.
    [Show full text]
  • 5-7 the Pythagorean Theorem 5-7 the Pythagorean Theorem
    55-7-7 TheThe Pythagorean Pythagorean Theorem Theorem Warm Up Lesson Presentation Lesson Quiz HoltHolt McDougal Geometry Geometry 5-7 The Pythagorean Theorem Warm Up Classify each triangle by its angle measures. 1. 2. acute right 3. Simplify 12 4. If a = 6, b = 7, and c = 12, find a2 + b2 2 and find c . Which value is greater? 2 85; 144; c Holt McDougal Geometry 5-7 The Pythagorean Theorem Objectives Use the Pythagorean Theorem and its converse to solve problems. Use Pythagorean inequalities to classify triangles. Holt McDougal Geometry 5-7 The Pythagorean Theorem Vocabulary Pythagorean triple Holt McDougal Geometry 5-7 The Pythagorean Theorem The Pythagorean Theorem is probably the most famous mathematical relationship. As you learned in Lesson 1-6, it states that in a right triangle, the sum of the squares of the lengths of the legs equals the square of the length of the hypotenuse. a2 + b2 = c2 Holt McDougal Geometry 5-7 The Pythagorean Theorem Example 1A: Using the Pythagorean Theorem Find the value of x. Give your answer in simplest radical form. a2 + b2 = c2 Pythagorean Theorem 22 + 62 = x2 Substitute 2 for a, 6 for b, and x for c. 40 = x2 Simplify. Find the positive square root. Simplify the radical. Holt McDougal Geometry 5-7 The Pythagorean Theorem Example 1B: Using the Pythagorean Theorem Find the value of x. Give your answer in simplest radical form. a2 + b2 = c2 Pythagorean Theorem (x – 2)2 + 42 = x2 Substitute x – 2 for a, 4 for b, and x for c. x2 – 4x + 4 + 16 = x2 Multiply.
    [Show full text]
  • Geometry ­ Ch 5 ­ Exterior Angles & Triangle Inequality December 01, 2014
    Geometry ­ Ch 5 ­ Exterior Angles & Triangle Inequality December 01, 2014 The “Three Possibilities” Property: either a>b, a=b, or a<b The Transitive Property: If a>b and b>c, then a>c The Addition Property: If a>b, then a+c>b+c The Subtraction Property: If a>b, then a‐c>b‐c The Multiplication Property: If a>b and c>0, then ac>bc The Division Property: If a>b and c>0, then a/c>b/c The Addition Theorem of Inequality: If a>b and c>d, then a+c>b+d The “Whole Greater than Part” Theorem: If a>0, b>0, and a+b=c, then c>a and c>b Def: An exterior angle of a triangle is an angle that forms a linear pair with an angle of the triangle. A In ∆ABC, exterior ∠2 forms a linear pair with ∠ACB. The other two angles of the triangle, ∠1 (∠B) and ∠A are called remote interior angles with respect to ∠2. 1 2 B C Theorem 12: The Exterior Angle Theorem An Exterior angle of a triangle is greater than either remote interior angle. Find each of the following sums. 3 4 26. ∠1+∠2+∠3+∠4 2 1 6 7 5 8 27. ∠1+∠2+∠3+∠4+∠5+∠6+∠7+ 9 12 ∠8+∠9+∠10+∠11+∠12 11 10 28. ∠1+∠5+∠9 31. What does the result in exercise 30 indicate about the sum of the exterior 29. ∠3+∠7+∠11 angles of a triangle? 30. ∠2+∠4+∠6+∠8+∠10+∠12 1 Geometry ­ Ch 5 ­ Exterior Angles & Triangle Inequality December 01, 2014 After proving the Exterior Angle Theorem, Euclid proved that, in any triangle, the sum of any two angles is less than 180°.
    [Show full text]
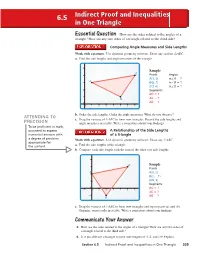
  • Indirect Proof and Inequalities in One Triangle
    6.5 Indirect Proof and Inequalities in One Triangle EEssentialssential QQuestionuestion How are the sides related to the angles of a triangle? How are any two sides of a triangle related to the third side? Comparing Angle Measures and Side Lengths Work with a partner. Use dynamic geometry software. Draw any scalene △ABC. a. Find the side lengths and angle measures of the triangle. 5 Sample C 4 Points Angles A(1, 3) m∠A = ? A 3 B(5, 1) m∠B = ? C(7, 4) m∠C = ? 2 Segments BC = ? 1 B AC = ? AB = 0 ? 01 2 34567 b. Order the side lengths. Order the angle measures. What do you observe? ATTENDING TO c. Drag the vertices of △ABC to form new triangles. Record the side lengths and PRECISION angle measures in a table. Write a conjecture about your fi ndings. To be profi cient in math, you need to express A Relationship of the Side Lengths numerical answers with of a Triangle a degree of precision Work with a partner. Use dynamic geometry software. Draw any △ABC. appropriate for the content. a. Find the side lengths of the triangle. b. Compare each side length with the sum of the other two side lengths. 4 C Sample 3 Points A A(0, 2) 2 B(2, −1) C 1 (5, 3) Segments 0 BC = ? −1 01 2 3456 AC = ? −1 AB = B ? c. Drag the vertices of △ABC to form new triangles and repeat parts (a) and (b). Organize your results in a table. Write a conjecture about your fi ndings.
    [Show full text]