DOCSLIB.ORG

Aspects of Gravitational Collapse and the Formation of Spacetime Singularities

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Aspects of Gravitational Collapse and the Formation of Spacetime Singularities Aspects of Gravitational Collapse and the formation of Spacetime Singularities Soumya Chakrabarti Department of Physical Sciences Indian Institute of Science Education and Research Kolkata Supervisor: Prof. Narayan Banerjee arXiv:1709.01512v1 [gr-qc] 5 Sep 2017 Thesis submitted to IISER Kolkata for the fulfilment of the requirements for the Degree of Doctor of Philosophy September 2017 To Mother... Declaration I certify that this work contains no material which has been accepted for the award of any other degree or diploma in my name, in any university or other tertiary institution, to the best of my knowledge and belief, contains no material previously published or written by another person, except where due reference has been made in the text and acknowledgement of collaborative research. In addition, I certify that no part of this work will, in the future, be used in a submission in my name, for any other degree or diploma in any university or other tertiary institution without the prior approval of Indian Institute of Science Education and Research Kolkata, India and collaborators. Soumya Chakrabarti Registration number: 10IP11 Department of Physical Sciences IISER Kolkata September 2017 Certificate This is to certify that the Ph.D. thesis entitled "Aspects of Gravitational Collapse and the formation of Spacetime Singularities" submitted by Soumya Chakrabarti is absolutely based upon his own work under the supervision of Prof. Narayan Banerjee at the Indian Institute of Science Education and Research, Kolkata (IISER Kolkata) and that neither this thesis nor any part of it has been submitted for either any degree/diploma or any other academic award anywhere before. Prof. Narayan Banerjee Professor Department of Physical Sciences IISER Kolkata Acknowledgements It is indeed a pleasure on my part to express my gratitude to my supervisor, Professor Narayan Banerjee. I would not be in my position today, without his support, guidance and his belief in me. At many times his insights and patience were the only things that came to my aid; academically or else. I owe my gratitude to Dr. Rituparno Goswami (University of KwaZulu Natal) for his ideas and helpful comments which helped me towards a deeper understanding of my work. My special thanks to Dr. Golam Mortuza Hossain (IISER Kolkata) for his help and valuable suggestions. During my stay at IISER Kolkata, it was a memorable experience with all my friends and colleagues. I was blessed to have seniors like Arghya Da, Nandan Da and Gopal Da from whom I learnt a lot through numerous ’interactive’ tea sessions. I thank all my juniors, Anushree, Chiranjib, Subhajit, Avijit, Srijita, Sachin; especially Chiranjib and Subhajit for making our days full of laughter and pratical jokes. I must thank all the other members of the Department Of Physical Sciences, IISER Kolkata, for their support and help. A very special gratitude to Debmalya who was a wonderful companion during this journey and at times was like an elder brother to me. I hope that we can continue to have even more refreshing conversations as we grow old and experienced. I would like to thank my batch-mate Ankan for being helpful in many difficult times. I wish him a lot of success in life. I am extremely indebted to my mother Sarbari Chakrabarti, who was my very first teacher and mentor, and never stopped dreaming for me. I wish that someday I would be a better son and give her a lot more peace, happiness and joyous memories and make her proud. I cannot end without thanking my grandfather, for encouraging my interest in mathematics when I was a child. I thank my sister and express my deepest affection. I wish her a lot of happiness in life. x To my father, I understand it is extremely difficult to grow up to become a man like you were. A day does not go by when I don’t miss you. I owe my heartiest gratitude and many colourful memories to Torsa, who never loses faith in me, being as loving, patient and charming as only she can be; to whom I dedicate these words... "Grow old with me, the best is yet to be..." Abstract Possibilities emerging out of the dynamical evolutions of collapsing systems are addressed in this thesis through analytical investigations of the highly non-linear Einstein Field Equations. Studies of exact solutions and their properties, play a non-trivial role in general relativity, even in the current context. Finding non-trivial solutions to the Einstein field equations requires some reduction of the problem, which usually is done by exploiting symmetries or other prop- erties. Exact solutions of the Einstein’s field equations describing an unhindered gravitational collapse are studied which generally predict an ultimate singular end-state. In the vicinity of such a spacetime singularity, the energy densities, spacetime curvatures, and all other physical quantities blow up. Despite exhaustive attempts over decades, the famous conjecture that the formation of a singularity during stellar collapse necessarily accompanies the formation of an event horizon, thereby covering the central singularity, still remains without a proof. Moreover, there are examples of stellar collapse models with reasonable matter contribution in which an event horizon does not form at all, giving rise to a naked singularity from which both matter and radiation can fall in and come out. These examples suggest that the so-called “cosmic censorship” conjecture may not be a general rule. Therefore one must embark upon analysis of realistic theoretical models of gravitational collapse and gradually generalizing previous efforts. Viable f (R) models are quite successful in providing a geometrical origin of the dark energy sector of the universe. However, they possess considerable problems in some other significant sectors, such as, difficulty to find exact solutions of the field equations whichare fourth order differential equations in the metric components. Moreover, a recent proposition that homogeneous collapsing stellar models (e.g. Oppenheimer-Snyder-Datt model of a col- lapsing homogeneous dust ball with an exterior Schwarzschild spacetime) of General Relativity can not be viable models in f (R) theories, heavily constrict the set of useful astrophysical solutions. In this thesis, we address some collapsing models in f (R) gravity such that at the comoving boundary of the collapsing star, the interior spacetime matches smoothly with an xii exterior spacetime. The presence and importance of spatial inhomogeneity is duely noted and discussed. The ultimate spacetime singularity remains hidden or exposed to an exterior observer depending on initial conditions from which the collapse evolves. The study of collapsing solutions of the Einstein equations with a scalar field as the matter contribution owes special importance, because one would like to know if cosmic censorship is necessarily preserved or violated in gravitational collapse for fundamental matter fields, which are derived from a suitable Lagrangian. In this thesis we have studied some models of gravitational collapse under spherical symmetry, with a self-interacting scalar field minimally coupled to gravity along with a fluid description. The field equations are solved under certain significant symmetry assumption at the outset (for instance, conformal flatness, self-similarity) without assuming any particular equation of state for the matter contribution. The relevance of such investigations stems from the present importance of a scalar field as the dark energy vis-a-vis the fluid, whose distribution still remains unknown apart from the general belief that the dark energy does not cluster at any scale below the Hubble scale. The study of collapse of scalar fields, particularly in the presence of a fluid may in some way enlighten usregarding the possible clustering of dark energy. The collapsing models are studied in this thesis for certain popular and physically significant forms of the self-interaction potential, for example, a power-law or an exponential dependence over the scalar field. The end-state of the collapse is investigated by analyzing the apparent horizon curve and existence of radial null geodesics emanating from the spacetime singularity. List of Publications 1. Soumya Chakrabarti and Narayan Banerjee, "Spherical Collapse in vacuum f(R) gravity", Astrophys. Space Sci. 354 (2014) no.2, 2118; Erratum: Astrophys. Space Sci. 359 (2015) no.1, 36. (Not included in the thesis) 2. Soumya Chakrabarti and Narayan Banerjee, "Spherically symmetric collapse of a perfect fluid in f(R) gravity", Gen. Relativ. Gravit. 48 : 57 (2016). 3. Soumya Chakrabarti and Narayan Banerjee, "Gravitational collapse in f(R) gravity for a spherically symmetric spacetime admitting a homothetic Killing vector", Eur. Phys. J. Plus 131 : 144 (2016). 4. Soumya Chakrabarti and Narayan Banerjee, "Scalar field collapse in a conformally flat spacetime", Eur. Phys. J. C. 77 no.3, 166 (2017). 5. Narayan Banerjee and Soumya Chakrabarti, "Self-similar scalar field collapse", Phys. Rev. D. 95, 024015 (2017). 6. Soumya Chakrabarti, "Scalar Field Collapse with an exponential potential", Gen. Relativ. Gravit. 49 : 24 (2017). Table of contents 1 Introduction1 1.1 Gravitational collapse and spacetime singularity . .1 1.1.1 Basic features of a Gravitational Collapse . .3 1.1.2 End-state of an unhindered Gravitational Collapse: Blackholes . .3 1.1.3 Naked Singularities . .4 1.1.4 Physical implications of a Naked Singularity . .6 1.1.5 Black Holes vs Naked Singularities . .8 1.2 Modified theory of gravity . .9 1.2.1 Motivation for modifying Gravity . 10 1.2.2 f (R) Gravity . 11 1.2.3 f (R) gravity in metric formalism . 13 1.2.4 Criteria for Viability . 13 1.2.5 f (R) models in the context of the present accelerated expansion of the universe . 16 1.2.6 Exact solutions and Gravitational Collapse in f (R) Gravity . 18 1.3 Introduction to Scalar Fields . 22 1.3.1 A brief review of Cosmological models based on scalar fields .
Load more

Recommended publications
  • Essays in Public Economics by Dorian Carloni a Dissertation Submitted In
    Essays in Public Economics by Dorian Carloni A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Economics in the Graduate Division of the University of California, Berkeley Committee in charge: Professor Alan J. Auerbach, Chair Professor Hilary W. Hoynes Professor Rucker C. Johnson Professor Emmanuel Saez Spring 2016 Essays in Public Economics Copyright 2016 by Dorian Carloni 1 Abstract Essays in Public Economics by Dorian Carloni Doctor of Philosophy in Economics University of California, Berkeley Professor Alan J. Auerbach, Chair This dissertation consists of three chapters and analyzes individuals' and firms’ response to tax and government spending policies. The first chapter focuses on the economic incidence of a large value added tax (VAT) cut in the restaurant industry in France. In particular it estimates the share of the tax cut falling on workers, firm owners and consumers by analyzing the VAT cut applied to French sit-down restaurants { a drop from 19.6 percent to 5.5 percent { in July 2009. Theoretically, we develop a standard partial equilibrium model of consumption tax incidence that includes consumption substitutability between the taxed good and an untaxed good, and markets for production inputs, which we allow to vary with the tax. Empirically, we use firm-level data and a difference-in-differences strategy to show that the reform increased restaurant profits and the cost of employees, and aggregate price data to estimate the decrease in prices produced by the reform. We compare sit-down restaurants to (a) non-restaurant market services and (b) non-restaurant small firms, and find that prices decreased by around 2 percent, the cost per employee increased by 3.9 percent and the return to capital increased by around 10 percent.
    [Show full text]
  • Generation of Angular Momentum in Cold Gravitational Collapse
    A&A 585, A139 (2016) Astronomy DOI: 10.1051/0004-6361/201526756 & c ESO 2016 Astrophysics Generation of angular momentum in cold gravitational collapse D. Benhaiem1,M.Joyce2,3, F. Sylos Labini4,1,5, and T. Worrakitpoonpon6 1 Istituto dei Sistemi Complessi Consiglio Nazionale delle Ricerche, via dei Taurini 19, 00185 Rome, Italy e-mail: [email protected] 2 UPMC Univ. Paris 06, UMR 7585, LPNHE, 75005 Paris, France 3 CNRS IN2P3, UMR 7585, LPNHE, 75005 Paris, France 4 Centro Studi e Ricerche Enrico Fermi, Via Panisperna 89 A, Compendio del Viminale, 00184 Rome, Italy 5 INFN Unit Rome 1, Dipartimento di Fisica, Universitá di Roma Sapienza, Piazzale Aldo Moro 2, 00185 Roma, Italy 6 Faculty of Science and Technology, Rajamangala University of Technology Suvarnabhumi, Nonthaburi Campus, 11000 Nonthaburi, Thailand Received 16 June 2015 / Accepted 4 November 2015 ABSTRACT During the violent relaxation of a self-gravitating system, a significant fraction of its mass may be ejected. If the time-varying gravi- tational field also breaks spherical symmetry, this mass can potentially carry angular momentum. Thus, starting initial configurations with zero angular momentum can, in principle, lead to a bound virialised system with non-zero angular momentum. Using numerical simulations we explore here how much angular momentum can be generated in a virialised structure in this way, starting from con- figurations of cold particles that are very close to spherically symmetric. For the initial configurations in which spherical symmetry is broken only by the Poissonian fluctuations associated with the finite particle number N, with N in range 103 to 105, we find that the relaxed structures have standard “spin” parameters λ ∼ 10−3, and decreasing slowly with N.
    [Show full text]
  • Special and General Relativity with Applications to White Dwarfs, Neutron Stars and Black Holes
    Norman K. Glendenning Special and General Relativity With Applications to White Dwarfs, Neutron Stars and Black Holes First Edition 42) Springer Contents Preface vii 1 Introduction 1 1.1 Compact Stars 2 1.2 Compact Stars and Relativistic Physics 5 1.3 Compact Stars and Dense-Matter Physics 6 2 Special Relativity 9 2.1 Lorentz Invariance 11 2.1.1 Lorentz transformations 11 2.1.2 Time Dilation 14 2.1.3 Covariant vectors 14 2.1.4 Energy and Momentum 16 2.1.5 Energy-momentum tensor of a perfect fluid 17 2.1.6 Light cone 18 3 General Relativity 19 3.1 Scalars, Vectors, and Tensors in Curvilinear Coordinates 20 3.1.1 Photon in a gravitational field 28 3.1.2 Tidal gravity 29 3.1.3 Curvature of spacetime 30 3.1.4 Energy conservation and curvature 30 3.2 Gravity 32 3.2.1 Einstein's Discovery 32 3.2.2 Particle Motion in an Arbitrary Gravitational Field 32 3.2.3 Mathematical definition of local Lorentz frames . 35 3.2.4 Geodesics 36 3.2.5 Comparison with Newton's gravity 38 3.3 Covariance 39 3.3.1 Principle of general covariance 39 3.3.2 Covariant differentiation 40 3.3.3 Geodesic equation from covariance principle 41 3.3.4 Covariant divergente and conserved quantities . 42 3.4 Riemann Curvature Tensor 45 x Contents 3.4.1 Second covariant derivative of scalars and vectors 45 3.4.2 Symmetries of the Riemann tensor 46 3.4.3 Test for flatness 47 3.4.4 Second covariant derivative of tensors 47 3.4.5 Bianchi identities 48 3.4.6 Einstein tensor 48 3.5 Einstein's Field Equations 50 3.6 Relativistic Stars 52 3.6.1 Metric in static isotropic spacetime 53
    [Show full text]
  • Ocn752505145-2018-11-02-By-Last-Name.Pdf (248.0Kb)
    System Inspectors Sorted by Last Name Total Count: 1424 SI# Expires Name Association Town State 14215 5/1/2021 Zachary D. Aaronson CDM Smith Providence RI 4698 6/30/2019 James Abare Winchendon MA 4046 6/30/2019 Stacey J. Abato Raggs, Inc. Concord MA 2548 6/30/2019 Carl Adamo Lincoln RI 349 6/30/2019 Stephen M. Adams Norwell MA 13724 6/30/2019 David R. Adler Charlton MA 14072 12/1/2019 Nicholas Aguiar Yarmouth DPW - Engineering Division West Yarmouth MA 4332 6/30/2019 James D. Aguiar, Jr. Tri-Spec Corp. Westport MA 14016 5/1/2020 Thorsen Akerley Williams & Sparages, LLC Middleton MA 13661 6/30/2019 Patrick Alderman Swansea MA 2040 6/30/2019 Michael Alesse East Coast Excavating Groveland MA 4789 6/30/2019 Lisa C. Allain Millbury MA 4955 6/30/2019 Mark Allain Peabody MA 12864 6/30/2020 William Allen Bill Allen Enterprises LLC Spring Hill FL 13850 6/30/2021 Edward W. Alleva Jr. Alleva Excavating Company Lunenburg MA 350 6/30/2019 Karl J. Alm Alm and Son Septic West Brookfield MA 14169 12/1/2020 Wyatt J. Alm West Brookfield MA 13975 4/1/2019 Elizabeth Alves All Clear Title 5 Services Norton MA 14252 8/1/2021 Nathon Amaral Mystic Excavating Corp Raynham MA 13218 6/30/2021 Erik Anderson Norwell MA 4658 6/30/2019 Michael Andrade Graves Engineering, Inc. Sutton MA 14210 5/1/2021 Samantha Andrews T. Silvia Excavating Swansea MA 2666 6/30/2019 John R. Andrews, III Andrews Survey & Engineers, Inc.
    [Show full text]
  • Entering New Waters at Pier 94 Leslie Weir
    the newsletter of the golden gate audubon society // vol. 103 no. 4 fall 2019 EntEring nEw watErs at PiEr 94 leslie weir ore than a million individual shore- M birds rely on the San Francisco Bay for at least some portion of their annual lifecycle. The Bay Area is classified as a site of hemispheric significance for migra- tory shorebirds by the Western Hemisphere Shorebird Reserve Network, and the Ramsar Convention on Wetlands has designated San Francisco Bay as a site of international sig- nificance for migratory waterfowl. More than 1,000 species of birds, mammals, and fish rely on the San Francisco Bay Estuary—the centerpiece of our region. CONTINUED on page 5 American Avocet at Pier 94. Bob Gunderson long enough to be restored for his aston- ishing journey. Ornithologists discovered that Blackpoll Warblers have the longest migratory route of any New World warbler. Every fall, these tiny 12-gram birds make a nonstop transatlantic flight from upper Canada to South America. Then, the fol- lowing spring, they reverse migrate to their breeding grounds. A few hours later, I checked on this exquisite feathered jewel. He was no longer quiet. I could hear him bouncing against the box top in a frenzied urge to leap up and fly south. I let him go and off he went—toward the Statue of Liberty, a fitting testament to his fortitude. I hoped that I had helped him a little. Cindy Margulis Like this Blackpoll Warbler’s drive to Male Blackpoll Warbler. migrate during the fall season, this is our time of transition at GGAS.
    [Show full text]
  • Stellar Equilibrium Vs. Gravitational Collapse
    Eur. Phys. J. H https://doi.org/10.1140/epjh/e2019-100045-x THE EUROPEAN PHYSICAL JOURNAL H Stellar equilibrium vs. gravitational collapse Carla Rodrigues Almeidaa Department I Max Planck Institute for the History of Science, Boltzmannstraße 22, 14195 Berlin, Germany Received 26 September 2019 / Received in final form 12 December 2019 Published online 11 February 2020 c The Author(s) 2020. This article is published with open access at Springerlink.com Abstract. The idea of gravitational collapse can be traced back to the first solution of Einstein's equations, but in these early stages, com- pelling evidence to support this idea was lacking. Furthermore, there were many theoretical gaps underlying the conviction that a star could not contract beyond its critical radius. The philosophical views of the early 20th century, especially those of Sir Arthur S. Eddington, imposed equilibrium as an almost unquestionable condition on theoretical mod- els describing stars. This paper is a historical and epistemological account of the theoretical defiance of this equilibrium hypothesis, with a novel reassessment of J.R. Oppenheimer's work on astrophysics. 1 Introduction Gravitationally collapsed objects are the conceptual precursor to black holes, and their history sheds light on how such a counter-intuitive idea was accepted long before there was any concrete proof of their existence. A black hole is a strong field structure of space-time surrounded by a unidirectional membrane that encloses a singularity. General relativity (GR) predicts that massive enough bodies will collapse into black holes. In fact, the first solution of Einstein's field equations implies the existence of black holes, but this conclusion was not reached at the time because the necessary logical steps were not as straightforward as they appear today.
    [Show full text]
  • Collapse of an Unstable Neutron Star to a Black Hole Matthias Hanauske (E-Mail:[email protected], Office: 02.232)
    Experiments in Computer Simulations : Collapse of an unstable Neutron Star to a Black Hole Matthias Hanauske (e-mail:[email protected], office: 02.232) 0 Class Information • application form : { if you want to do this experiment, please register via e-mail to me no later than on the last Wednesday before the week in which you want to do the experiment; your e-mail should include the following information: (1) student number, (2) full name, (3) e-mail address. • intensive course : { 12 [hours] = 6 [hours/week] × 2 [weeks]. • when : { Monday 9-16, two subsequent weeks upon individual arrangement with me; other time slots may be arranged with me individually. • where : { Pool Room 01.120. • preparation : { an account for you on the \FUCHS" cluster of the CSC (http://csc.uni-frankfurt.de/) will be provided; please read the quick starting guide on the CSC web pages before starting the simulation. • required skill : { basic Linux knowledge. • using software : { Einstein Toolkit [5]. { gnuplot (http://www.gnuplot.info/) { pygraph (https://bitbucket.org/dradice/pygraph). { python (https://www.python.org/) and matplotlib (http://matplotlib.org/). { Mathematica (http://www.wolfram.com/mathematica/). 1 1 Introduction Neutron stars are beside white dwarfs and black holes the potential final states of the evo- lution of a normal star. These extremely dense astrophysical objects, which are formed in the center of a supernova explosion, represent the last stable state before the matter collapses to a black hole. Due to their large magnetic fields (up to 1011 Tesla) and fast rotation (up to 640 rotations in one second) neutron stars emit a certain electromagnetic spectrum.
    [Show full text]
  • Detection of Gravitational Collapse J
    Detection of gravitational collapse J. Craig Wheeler and John A. Wheeler Citation: AIP Conference Proceedings 96, 214 (1983); doi: 10.1063/1.33938 View online: http://dx.doi.org/10.1063/1.33938 View Table of Contents: http://scitation.aip.org/content/aip/proceeding/aipcp/96?ver=pdfcov Published by the AIP Publishing Articles you may be interested in Chaos and Vacuum Gravitational Collapse AIP Conf. Proc. 1122, 172 (2009); 10.1063/1.3141244 Dyadosphere formed in gravitational collapse AIP Conf. Proc. 1059, 72 (2008); 10.1063/1.3012287 Gravitational Collapse of Massive Stars AIP Conf. Proc. 847, 196 (2006); 10.1063/1.2234402 Analytical modelling of gravitational collapse AIP Conf. Proc. 751, 101 (2005); 10.1063/1.1891535 Gravitational collapse Phys. Today 17, 21 (1964); 10.1063/1.3051610 This article is copyrighted as indicated in the article. Reuse of AIP content is subject to the terms at: http://scitation.aip.org/termsconditions. Downloaded to IP: 128.83.205.78 On: Mon, 02 Mar 2015 21:02:26 214 DETECTION OF GRAVITATIONAL COLLAPSE J. Craig Wheeler and John A. Wheeler University of Texas, Austin, TX 78712 ABSTRACT At least one kind of supernova is expected to emit a large flux of neutrinos and gravitational radiation because of the collapse of a core to form a neutron star. Such collapse events may in addition occur in the absence of any optical display. The corresponding neutrino bursts can be detected via Cerenkov events in the same water used in proton decay experiments. Dedicated equipment is under construction to detect the gravitational radiation.
    [Show full text]
  • Priests and Deacons INDEX Archdiocesan Priests
    Priests and Deacons INDEX Archdiocesan Priests ..................................................................................................... 1 Priests of the Archdiocese in the Order of Ordination ................................................. 14 Priests and Deacons: Alphabetical Necrology ............................................................ 21 Priests and Deacons: Chronological Necrology by Month, Day and Year .................. 51 Archdiocesan Permanent Deacons ............................................................................ 79 11/30/2020 Archdiocesan Priests Adams, Rev. John E. (1969) Baer, Rev. Timothy K. (1996) Director, S.O.M.E., DC Pastor, St. Nicholas, Laurel Phone: 202-832-9710 Phone: 301-490-5116 Aguirre, Rev. Francisco E. (2013) Baraki, Rev. Tesfamariam (1975) Pastor, St. Catherine Labouré, Chaplain, Howard University Hospital, Wheaton DC Phone: 301-946-3636 In Residence, St. Gabriel, DC Phone: 202-726-9092 Agustin Rev. Patrick S. (2020) Parochial Vicar (pro-tem), St. Francis of Barbieri de Carvalho, Rev. Rafael Assisi, Dearwood (2013) Phone: 301-840-1407 Director of Spiritual Formation, Redemptoris Mater Archdiocesan Ailer, Rev. Gellert J. (2006) Missionary Seminary, Hyattsville Missionary Assignment, Archdiocese of Eger, Hungary Barry, Rev. John M. (1988) Pastor, Church of the Resurrection, Alliata, Rev. Peter R. (1961) Burtonsville Retired, St. John Vianney, Prince Phone: 301-236-5200 Frederick Phone: 301-440-1784 Bava, Rev. David A. (1973) Pastor, Holy Redeemer, DC Amey, Rev. Msgr. Robert
    [Show full text]
  • Swift J164449. 3+ 573451 Event: Generation in the Collapsing Star
    Swift J164449.3+573451 event: generation in the collapsing star cluster? V.I. Dokuchaev∗ and Yu.N. Eroshenko† Institute for Nuclear Research of the Russian Academy of Sciences 60th October Anniversary Prospect 7a, 117312 Moscow, Russia (Dated: June 27, 2018) We discuss the multiband energy release in a model of a collapsing galactic nucleus, and we try to interpret the unique super-long cosmic gamma-ray event Swift J164449.3+573451 (GRB 110328A by early classification) in this scenario. Neutron stars and stellar-mass black holes can form evolutionary a compact self-gravitating subsystem in the galactic center. Collisions and merges of these stellar remnants during an avalanche contraction and collapse of the cluster core can produce powerful events in different bands due to several mechanisms. Collisions of neutron stars and stellar-mass black holes can generate gamma-ray bursts (GRBs) similar to the ordinary models of short GRB origin. The bright peaks during the first two days may also be a consequence of multiple matter supply (due to matter release in the collisions) and accretion onto the forming supermassive black hole. Numerous smaller peaks and later quasi-steady radiation can arise from gravitational lensing, late accretion of gas onto the supermassive black hole, and from particle acceleration by shock waves. Even if this model will not reproduce exactly all the Swift J164449.3+573451 properties in future observations, such collapses of galactic nuclei can be available for detection in other events. PACS numbers: 98.54.Cm, 98.70.Rz Keywords: galactic nuclei; neutron stars; gamma-ray bursts I. INTRODUCTION ters of stellar remnants can form in the course of evolu- tion due to mass segregationsinking of the most massive On March 28, 2011, the Swift’s Burst Alert Telescope stars to the center and their explosions as supernovae [9– detected the unusual super-long gamma-ray event Swift 11].
    [Show full text]
  • Fuzzy Blackholes Anand Murugan Pomona College
    Claremont Colleges Scholarship @ Claremont Pomona Senior Theses Pomona Student Scholarship 2007 Fuzzy Blackholes Anand Murugan Pomona College Recommended Citation Murugan, Anand, "Fuzzy Blackholes" (2007). Pomona Senior Theses. 21. http://scholarship.claremont.edu/pomona_theses/21 This Open Access Senior Thesis is brought to you for free and open access by the Pomona Student Scholarship at Scholarship @ Claremont. It has been accepted for inclusion in Pomona Senior Theses by an authorized administrator of Scholarship @ Claremont. For more information, please contact [email protected]. Fuzzy Blackholes Anand Murugan Advisor : Prof. Vatche Sahakian May 1, 2007 Contents 1 Introduction 2 2 Background 3 2.1 String Theory And Her Mothers, Sisters and Daughters . 3 2.2 Black Holes And Their Properties . 5 2.3Holography................................ 7 2.4NCSYMs................................. 9 3 Fuzzy Black Holes 12 3.1 Formation of the Fuzzy Horizon . 12 3.2TheNCSYM............................... 13 3.3 The Gravitational Dual . 14 3.4 The Decoupling Limit . 16 3.5 Phase Structure . 18 3.6 Stabilization . 19 4 Brane Interaction 21 4.1 Setup of Problem . 21 4.2Analysis.................................. 22 5 Conclusions 23 1 Chapter 1 Introduction The fuzzball model of a black hole is an attempt to resolve the many paradoxes and puzzles of black hole physics that have revealed themselves over the last century. These badly behaved solutions of general relativity have given physicists one of the few laboratories to test candidate quantum theories of gravity. Though little is known about exactly what lies beyond the event horizon, and what the ultimate fate of matter that falls in to a black hole is, we know a few intriguing and elegant semi-classical results that have kept physicists occupied.
    [Show full text]
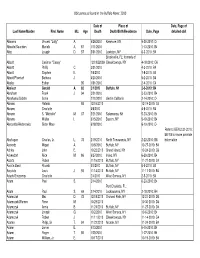
  • Obituaries Buffalo News 2010 by Name
    Obituaries as found in the Buffalo News: 2010 Date of Place of Date, Page of Last Name/Maiden First Name M.I. Age Death Death/Birth/Residence Date, Page detailed obit Abbarno Vincent "Lolly" A. 9/26/2010 Kenmore, NY 9-30-2010: C4 Abbatte/Saunders Murielle A. 87 1/11/2010 1-13-2010: B4 Abbo Joseph D. 57 5/31/2010 Lewiston, NY 6-3-2010: B4 Brooksville, FL; formerly of Abbott Casimer "Casey" 12/19/22009 Cheektowaga, NY 4-18-2010: C6 Abbott Phillip C. 3/31/2010 4-3-2010: B4 Abbott Stephen E. 7/6/2010 7-8-2010: B4 Abbott/Pfoetsch Barbara J. 4/20/2010 5-2-2010: B4 Abeles Esther 95 1/31/2010 2-4-2010: C4 Abelson Gerald A. 82 2/1/2010 Buffalo, NY 2-3-2010: B4 Abraham Frank J. 94 3/21/2010 3-23-2010: B4 Abrahams/Gichtin Sonia 2/10/2010 died in California 2-14-2010: C4 Abramo Rafeala 93 12/16/2010 12-19-2010: C4 Abrams Charlotte 4/6/2010 4-8-2010: B4 Abrams S. "Michelle" M. 37 5/21/2010 Salamanca, NY 5-23-2010: B4 Abrams Walter I. 5/15/2010 Basom, NY 5-19-2010: B4 Abrosette/Aksterowicz Sister Mary 6/18/2010 6-19-2010: C4 Refer to BEN 2-21-2010: B6/7/8 for more possible Abshagen Charles, Jr. L. 73 2/19/2010 North Tonawanda, NY 2-22-2010: B8 information Acevedo Miguel A. 10/6/2010 Buffalo, NY 10-27-2010: B4 Achkar John E.
    [Show full text]